2020-2021学年河北省沧州市任丘市七年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年河北省沧州市任丘市七年级(下)期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 222.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 00:00:00 | ||
图片预览




文档简介
2020-2021学年河北省沧州市任丘市七年级(下)期末数学试卷
一、正确选择.(本大题10个小题,每小题2分,共20分)
1.(2分)关于x,y的方程组的解为( )
A.
B.
C.
D.
2.(2分)下列命题是真命题的( )
A.两点之间直线最短
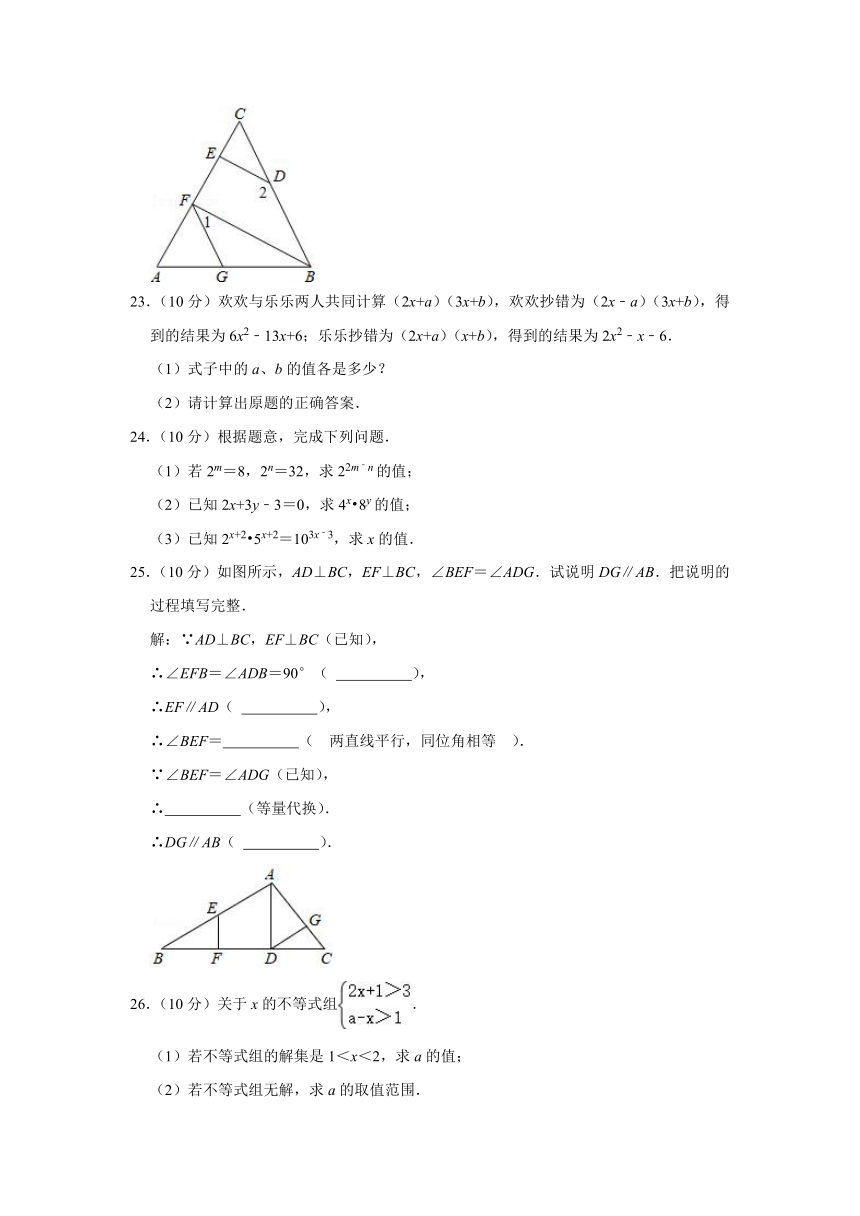
B.如果ab>0,那么a>0,b>0
C.内错角相等,两直线平行
D.若|a|=1,则a=1
3.(2分)如图,AB∥CD,点O在AB上,OE平分∠BOD,若∠CDO=100°,则∠BOE的度数为( )
A.30°
B.40°
C.50°
D.60°
4.(2分)已知三条线段长分别为2cm、4cm、acm,若这三条线段首尾顺次联结能围成一个三角形,那么a的取值可以是( )
A.1cm
B.2cm
C.4cm
D.7cm
5.(2分)下列现象中,( )是平移.
A.“天问”探测器绕火星运动
B.篮球在空中飞行
C.电梯的上下移动
D.将一张纸对折
6.(2分)据国家邮政局统计,2021年农历除夕和初一两天,全国快递处理超130
000
000件,与去年同期相比增长223%,快递的春节“不打烊”服务确保了广大用户能够顺利收到年货,欢度佳节.将130
000
000用科学记数法表示应为( )
A.1.3×107
B.13×107
C.1.3×108
D.0.13×109
7.(2分)下列运算中,正确的是( )
A.a5+a5=a10
B.3a3?2a2=6a6
C.a6÷a2=a3
D.(﹣3ab)2=9a2b2
8.(2分)下列关系式中,不含有x=﹣1这个解的是( )
A.2x+1=﹣1
B.2x+1>﹣1
C.﹣2x+1≥3
D.﹣2x﹣1≤3
9.(2分)已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b
B.a+2>b+2
C.﹣a<﹣b
D.2a>3b
10.(2分)笔记本4元/本,钢笔5元/支,某同学购买笔记本和钢笔恰好用去162元,那么最多购买钢笔( )支.
A.28
B.29
C.30
D.31
二、准确填空.(本大题10个小题,每小题3分,共30分)
11.(3分)若方程(m﹣4)x|m|﹣3=3yn+1+4是二元一次方程,则m=
,n=
.
12.(3分)已知x、y满足方程组,则x+y的值为
.
13.(3分)如图,直线AB和CD相交于O点,OM⊥AB,∠BOD:∠COM=1:3,则∠AOD的度数为
度.
14.(3分)如图,直线l1,l2被l3所截,下列条件:①∠1=∠2;②∠3=∠4;③l1∥l2,其中能判断AC∥BD的条件是
.
15.(3分)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,∠BCD=40°,则∠BED的度数为
.
16.(3分)如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=39°,则∠2的度数是
.
17.(3分)已知am=6,an=3,则am+n=
.
18.(3分)“x与5的差不小于x的3倍”用不等式表示为
.
19.(3分)若关于x的不等式的非负整数解只有3个,则m的取值范围是
.
20.(3分)因式分解:ax2﹣a=
.
三、解答题.(本大题7个小题,共70分)
21.(10分)一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
22.(10分)如图,∠AGF=∠ABC,∠1+∠2=180°,
(1)求证;BF∥DE.
(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数.
23.(10分)欢欢与乐乐两人共同计算(2x+a)(3x+b),欢欢抄错为(2x﹣a)(3x+b),得到的结果为6x2﹣13x+6;乐乐抄错为(2x+a)(x+b),得到的结果为2x2﹣x﹣6.
(1)式子中的a、b的值各是多少?
(2)请计算出原题的正确答案.
24.(10分)根据题意,完成下列问题.
(1)若2m=8,2n=32,求22m﹣n的值;
(2)已知2x+3y﹣3=0,求4x?8y的值;
(3)已知2x+2?5x+2=103x﹣3,求x的值.
25.(10分)如图所示,AD⊥BC,EF⊥BC,∠BEF=∠ADG.试说明DG∥AB.把说明的过程填写完整.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°(
),
∴EF∥AD(
),
∴∠BEF=
( 两直线平行,同位角相等 ).
∵∠BEF=∠ADG(已知),
∴
(等量代换).
∴DG∥AB(
).
26.(10分)关于x的不等式组.
(1)若不等式组的解集是1<x<2,求a的值;
(2)若不等式组无解,求a的取值范围.
27.(10分)(1)简便计算:992﹣108×92;
(2)因式分解:2x3﹣8x2+8x.
2020-2021学年河北省沧州市任丘市七年级(下)期末数学试卷
参考答案与试题解析
一、正确选择.(本大题10个小题,每小题2分,共20分)
1.(2分)关于x,y的方程组的解为( )
A.
B.
C.
D.
【分析】利用加减消元法求解即可.
【解答】解:,
①﹣②,得x=﹣4,
把x=﹣4代入②,得﹣4+y=3,解得y=7.
故方程组的解为.
故选:A.
2.(2分)下列命题是真命题的( )
A.两点之间直线最短
B.如果ab>0,那么a>0,b>0
C.内错角相等,两直线平行
D.若|a|=1,则a=1
【分析】利用线段的性质、不等式的性质、平行线的判定及绝对值的意义分别判断后即可确定正确的选项.
【解答】解:A、两点之间线段最短,故原命题错误,是假命题,不符合题意;
B、如果ab>0,那么a>0,b>0或a<0,b<0,故原命题错误,是假命题,不符合题意;
C、内错角相等,两直线平行,正确,是真命题,符合题意;
D、若|a|=1,则a=±1,故原命题错误,是假命题,不符合题意,
故选:C.
3.(2分)如图,AB∥CD,点O在AB上,OE平分∠BOD,若∠CDO=100°,则∠BOE的度数为( )
A.30°
B.40°
C.50°
D.60°
【分析】根据平行线的性质可得∠BOD=100°,利用角平分线的性质可得∠BOE=50°.
【解答】解:∵AB∥CD,∠CDO=100°,
∴∠BOD=100°,
∵OE平分∠BOD,
∴∠BOE=50°.
故选:C.
4.(2分)已知三条线段长分别为2cm、4cm、acm,若这三条线段首尾顺次联结能围成一个三角形,那么a的取值可以是( )
A.1cm
B.2cm
C.4cm
D.7cm
【分析】根据三角形的三边关系确定a的取值范围即可求解.
【解答】解:依题意有4﹣2<a<4+2,
解得:2<a<6.
只有选项C在范围内.
故选:C.
5.(2分)下列现象中,( )是平移.
A.“天问”探测器绕火星运动
B.篮球在空中飞行
C.电梯的上下移动
D.将一张纸对折
【分析】要根据平移的性质,判断是否是平移现象,平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形).
【解答】解:A.“天问”探测器绕火星运动不是平移;
B.篮球在空中飞行不是平移;
C.电梯的上下移动是平移;
D.将一张纸对折不是平移;
故选:C.
6.(2分)据国家邮政局统计,2021年农历除夕和初一两天,全国快递处理超130
000
000件,与去年同期相比增长223%,快递的春节“不打烊”服务确保了广大用户能够顺利收到年货,欢度佳节.将130
000
000用科学记数法表示应为( )
A.1.3×107
B.13×107
C.1.3×108
D.0.13×109
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:130000000=1.3×108.
故选:C.
7.(2分)下列运算中,正确的是( )
A.a5+a5=a10
B.3a3?2a2=6a6
C.a6÷a2=a3
D.(﹣3ab)2=9a2b2
【分析】根据同底数幂的乘除法,幂的乘方与积的乘方的计算方法逐项计算即可.
【解答】解:A.a5+a5=2a5,因此选项A不符合题意;
B.3a3?2a2=6a5,因此选项B不符合题意;
C.a6÷a2=a4,因此选项C不符合题意;
D.(﹣3ab)2=9a2b2,因此选项D符合题意;
故选:D.
8.(2分)下列关系式中,不含有x=﹣1这个解的是( )
A.2x+1=﹣1
B.2x+1>﹣1
C.﹣2x+1≥3
D.﹣2x﹣1≤3
【分析】把x=﹣1代入各个不等式,满足不等式成立时,它就是该不等式的解.
【解答】解:当x=﹣1时,2x+1=﹣1,﹣2x+1=3≥3,﹣2x﹣1=1≤3,
所以x=﹣1满足选项A、C、D,因为﹣1不大于﹣1,所以x=﹣1不满足B.
故选:B.
9.(2分)已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b
B.a+2>b+2
C.﹣a<﹣b
D.2a>3b
【分析】根据不等式的性质即可得到a>b,a+2>b+2,﹣a<﹣b.
【解答】解:由不等式的性质得a>b,a+2>b+2,﹣a<﹣b.
故选:D.
10.(2分)笔记本4元/本,钢笔5元/支,某同学购买笔记本和钢笔恰好用去162元,那么最多购买钢笔( )支.
A.28
B.29
C.30
D.31
【分析】设该同学购买钢笔x支,笔记本y本,根据总价=单价×数量,即可得出关于x,y的二元一次方程,结合x,y均为正整数,即可得出各购买方案,取x的最大值即可得出结论.
【解答】解:设该同学购买钢笔x支,笔记本y本,
依题意得:5x+4y=162.
∵x,y均为正整数,
∴或或或或或或或,
∴x的最大值为30.
故选:C.
二、准确填空.(本大题10个小题,每小题3分,共30分)
11.(3分)若方程(m﹣4)x|m|﹣3=3yn+1+4是二元一次方程,则m= ﹣4 ,n= 0 .
【分析】二元一次方程就是只含有两个未知数,并且未知数的项的次数是1的整式方程,依据定义即可求解.
【解答】解:根据题意,得
|m|﹣3=1且n+1=1且m﹣4≠0,
解得m=﹣4,n=0.
故答案为:﹣4,0.
12.(3分)已知x、y满足方程组,则x+y的值为
5 .
【分析】将两式相加即可.
【解答】解:两式相加得3x+3y=15,
x+y=5.
故答案为:5.
13.(3分)如图,直线AB和CD相交于O点,OM⊥AB,∠BOD:∠COM=1:3,则∠AOD的度数为 157.5 度.
【分析】先根据OM⊥AB,得∠BOM=90°,再∠BOD:∠COM=1:3,可求出∠DOB,再根据平角关系,即可得出∠AOD的度数.
【解答】解:∵OM⊥AB,
∴∠BOM=90°,
∴∠BOD+∠COM=90°,
∵∠BOD:∠COM=1:3,
∴∠BOD=22.5°,
∵∠AOB=180°,
∴∠AOD=∠AOB﹣∠BOD=157.5°.
故答案为:157.5.
14.(3分)如图,直线l1,l2被l3所截,下列条件:①∠1=∠2;②∠3=∠4;③l1∥l2,其中能判断AC∥BD的条件是
① .
【分析】根据同位角相等,两直线平行即可判断AC∥BD.
【解答】解:①∵∠1=∠2,
∴AC∥BD(同位角相等,两直线平行).
故答案为:①.
15.(3分)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,∠BCD=40°,则∠BED的度数为 60° .
【分析】先根据角平分线的定义,得出∠ABE=∠CBE=∠ABC,∠ADE=∠CDE=∠ADC,再根据三角形内角和定理,推理得出∠BAD+∠BCD=2∠E,进而求得∠E的度数.
【解答】解:∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠CBE=∠ABC,∠ADE=∠CDE=∠ADC,
∵∠ABE+∠BAD=∠E+∠ADE,∠BCD+∠CDE=∠E+∠CBE,
∴∠ABE+∠BAD+∠BCD+∠CDE=∠E+∠ADE+∠E+∠CBE,
∴∠BAD+∠BCD=2∠E,
∵∠BAD=80°,∠BCD=40°,
∴∠E=(∠BAD+∠BCD)=(80°+40°)=60°.
故答案为:60°.
16.(3分)如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=39°,则∠2的度数是
21° .
【分析】过B作BC∥l1,可得∠2=∠ABC,由平行公理可得BC∥l2,根据平行线的性质可得∠1+∠2=∠ABD,结合直角三角板的特性可求解.
【解答】解:如图,过B作BC∥l1,
∴∠2=∠ABC,
∵l2∥l1,
∴BC∥l2,
∴∠CBD=∠1,
∴∠1+∠2=∠ABC+∠CBD=∠ABD,
由题意知:∠ABD=60°,
∴∠1+∠2=60°,
∵∠1=39°,
∴∠2=60°﹣39°=21°,
故答案为21°.
17.(3分)已知am=6,an=3,则am+n= 18 .
【分析】根据同底数幂的乘法底数不变指数相加,可得答案.
【解答】解:am+n=am?an=6×3=18,
故答案为:18.
18.(3分)“x与5的差不小于x的3倍”用不等式表示为
x﹣5≥3x .
【分析】根据x与5的差不小于x的3倍,可知x与5的差大于等于x的3倍,从而可以用相应的不等式表示出来.
【解答】解:“x与5的差不小于x的3倍”用不等式表示为x﹣5≥3x,
故答案为:x﹣5≥3x.
19.(3分)若关于x的不等式的非负整数解只有3个,则m的取值范围是
<m≤1 .
【分析】首先确定不等式组的解集,先利用含m的式子表示,根据非负整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于m的不等式,从而求出m的范围.
【解答】解:解不等式,得:x<3m,
∵关于x的不等式的非负整数解只有3个,
∴不等式的非负整数解为0、1、2,
则2<3m≤3,
解得:<m≤1,
故答案为:<m≤1.
20.(3分)因式分解:ax2﹣a= a(x+1)(x﹣1) .
【分析】首先提公因式a,再利用平方差进行二次分解即可.
【解答】解:原式=a(x2﹣1)=a(x+1)(x﹣1).
故答案为:a(x+1)(x﹣1).
三、解答题.(本大题7个小题,共70分)
21.(10分)一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
【分析】(1)设甲组工作一天商店应付x元,乙组工作一天商店应付y元,根据“若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据所需总费用=每天应付钱数×工作天数,分别求出单独请甲、乙两组完成所需费用,比较后即可得出结论;
(3)根据损失总钱数=每天盈利×装修时间+装修队所需费用,分别求出单独请甲、乙两组及请甲乙两组同时完成所损失的总钱数,比较后即可得出结论.
【解答】解:(1)设甲组工作一天商店应付x元,乙组工作一天商店应付y元,
根据题意得:,
解得:.
答:甲组工作一天商店应付300元,乙组工作一天商店应付140元.
(2)单独请甲组所需费用为:300×12=3600(元),
单独请乙组所需费用为:140×24=3360(元),
∵3600>3360,
∴单独请乙组所需费用最少.
(3)商店请甲乙两组同时装修,才更有利,理由如下:
单独请甲组完成,损失钱数为:200×12+3600=6000(元),
单独请乙组完成,损失钱数为:200×24+3360=8160(元),
请甲乙两组同时完成,损失钱数为:200×8+3520=5120(元).
∵8160>6000>5120,
∴商店请甲乙两组同时装修,才更有利.
22.(10分)如图,∠AGF=∠ABC,∠1+∠2=180°,
(1)求证;BF∥DE.
(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数.
【分析】(1)根据∠AGF=∠ABC可得出BC∥GF,进而可得出∠AFG=∠C,再根据角的计算可得出∠1=∠CDE,由此即可得出∠CED=∠CFB,根据“同位角相等,两直线平行”即可得出BF∥DE;
(2)根据DE⊥AC、BF∥DE即可得出∠AFB=90°,再结合∠1+∠2=180°、∠2=150°以及∠AFB=∠AFG+∠1即可算出∠AFG的度数.
【解答】(1)证明:∵∠AGF=∠ABC,
∴BC∥GF,
∴∠AFG=∠C.
∵∠1+∠2=180°,∠CDE+∠2=180°,
∴∠1=∠CDE.
∵∠CED=180°﹣∠C﹣∠CDE,∠CFB=180°﹣∠AFD﹣∠1,
∴∠CED=∠CFB,
∴BF∥DE.
(2)解:∵DE⊥AC,BF∥DE,
∴∠AFB=∠AED=90°,
∵∠1+∠2=180°,∠2=150°,
∴∠1=30°.
∵∠AFB=∠AFG+∠1=90°,
∴∠AFG=60°.
23.(10分)欢欢与乐乐两人共同计算(2x+a)(3x+b),欢欢抄错为(2x﹣a)(3x+b),得到的结果为6x2﹣13x+6;乐乐抄错为(2x+a)(x+b),得到的结果为2x2﹣x﹣6.
(1)式子中的a、b的值各是多少?
(2)请计算出原题的正确答案.
【分析】(1)根据由于欢欢抄错了第一个多项式中的a符号,得出的结果为6x2﹣13x+6,可知(2x﹣a)(3x+b)=6x2+(2b﹣3a)x﹣ab=6x2﹣13x+6,于是2b﹣3a=﹣13①;再根据乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2﹣x﹣6,可知常数项是﹣6,可知(2x+a)(x+b)=2x2﹣x﹣6,可得到2b+a=﹣1②,解关于①②的方程组即可求出a、b的值;
(2)把a、b的值代入原式求出整式乘法的正确结果.
【解答】解:(1)根据题意可知,由于欢欢抄错了第一个多项式中的a的符号,得到的结果为6x2﹣13x+6,
那么(2x﹣a)(3x+b)=6x2+(2b﹣3a)x﹣ab=6x2﹣13x+6,
可得2b﹣3a=﹣13
①
乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2﹣x﹣6,
可知(2x+a)(x+b)=2x2﹣x﹣6
即2x2+(2b+a)x+ab=2x2﹣x﹣6,
可得2b+a=﹣1
②,
解关于①②的方程组,可得a=3,b=﹣2;
(2)正确的式子:
(2x+3)(3x﹣2)=6x2+5x﹣6
24.(10分)根据题意,完成下列问题.
(1)若2m=8,2n=32,求22m﹣n的值;
(2)已知2x+3y﹣3=0,求4x?8y的值;
(3)已知2x+2?5x+2=103x﹣3,求x的值.
【分析】(1)直接利用同底数幂的除法运算法则以及幂的乘方运算法则将原式变形,进而得出答案;
(2)直接利用同底数幂的乘法运算法则以及幂的乘方运算法则将原式变形进,而得出答案;
(3)直接利用同底数幂的乘法运算法则以及积的乘方运算法则将原式变形进,而得出答案.
【解答】解:(1)∵2m=8,2n=32,
∴22m﹣n=(2m)2÷2n=82÷32=64÷32=2;
∴22m﹣n的值为2;
(2)∵2x+3y﹣3=0,
∴2x+3y=3,
∴4x?8y=22x?23y=22x+3y=23=8;
∴4x?8y的值为8;
(3)∵2x+2?5x+2=10x+2,
∴10x+2=103x﹣3,
∴x+2=3x﹣3,
∴,
∴x的值为.
25.(10分)如图所示,AD⊥BC,EF⊥BC,∠BEF=∠ADG.试说明DG∥AB.把说明的过程填写完整.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°(
垂直的定义 ),
∴EF∥AD(
同位角相等,两直线平行 ),
∴∠BEF= ∠BAD ( 两直线平行,同位角相等 ).
∵∠BEF=∠ADG(已知),
∴ ∠ADG=∠BAD (等量代换).
∴DG∥AB(
内错角相等,两直线平行 ).
【分析】根据垂直的定义得出∠EFB=∠ADB=90°,即可判定EF∥AD,则得出∠BEF=∠BAD,等量代换得出∠ADG=∠BAD,即可判定DG∥AB.
【解答】解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°(垂直的定义),
∴EF∥AD(同位角相等,两直线平行),
∴∠BEF=∠BAD(两直线平行,同位角相等),
∵∠BEF=∠ADG(已知),
∴∠ADG=∠BAD(等量代换),
∴DG∥AB(内错角相等,两直线平行).
故答案为:垂直的定义;同位角相等,两直线平行;∠BAD;∠ADG=∠BAD;内错角相等,两直线平行.
26.(10分)关于x的不等式组.
(1)若不等式组的解集是1<x<2,求a的值;
(2)若不等式组无解,求a的取值范围.
【分析】(1)解不等式组中两个不等式后根据不等式组的解集可得关于a的方程,解之可得;
(2)根据“大小小大无解了”可确定关于a的不等式,解之可得.
【解答】解:(1)解不等式2x+1>3得:x>1,
解不等式a﹣x>1得:x<a﹣1,
∵不等式组的解集是1<x<2,
∴a﹣1=2,
解得:a=3;
(2)∵不等式组无解,
∴a﹣1≤1,
解得:a≤2.
27.(10分)(1)简便计算:992﹣108×92;
(2)因式分解:2x3﹣8x2+8x.
【分析】(1)把992﹣108×92写成(100﹣1)2﹣(100+8)(100﹣)的形式,再利用完全平方公式和平方差进行计算即可.
(2)首先提取公因式2x,再进一步运用完全平方公式计算即可解答.
【解答】解:(1)992﹣108×92
=(100﹣1)2﹣(100+8)(100﹣8)
=1002﹣200+1﹣1002+82
=﹣200+1+64
=﹣135;
(2)原式=2x(x2﹣4x+4)
=2x(x﹣2)2.
一、正确选择.(本大题10个小题,每小题2分,共20分)
1.(2分)关于x,y的方程组的解为( )
A.
B.
C.
D.
2.(2分)下列命题是真命题的( )
A.两点之间直线最短
B.如果ab>0,那么a>0,b>0
C.内错角相等,两直线平行
D.若|a|=1,则a=1
3.(2分)如图,AB∥CD,点O在AB上,OE平分∠BOD,若∠CDO=100°,则∠BOE的度数为( )
A.30°
B.40°
C.50°
D.60°
4.(2分)已知三条线段长分别为2cm、4cm、acm,若这三条线段首尾顺次联结能围成一个三角形,那么a的取值可以是( )
A.1cm
B.2cm
C.4cm
D.7cm
5.(2分)下列现象中,( )是平移.
A.“天问”探测器绕火星运动
B.篮球在空中飞行
C.电梯的上下移动
D.将一张纸对折
6.(2分)据国家邮政局统计,2021年农历除夕和初一两天,全国快递处理超130
000
000件,与去年同期相比增长223%,快递的春节“不打烊”服务确保了广大用户能够顺利收到年货,欢度佳节.将130
000
000用科学记数法表示应为( )
A.1.3×107
B.13×107
C.1.3×108
D.0.13×109
7.(2分)下列运算中,正确的是( )
A.a5+a5=a10
B.3a3?2a2=6a6
C.a6÷a2=a3
D.(﹣3ab)2=9a2b2
8.(2分)下列关系式中,不含有x=﹣1这个解的是( )
A.2x+1=﹣1
B.2x+1>﹣1
C.﹣2x+1≥3
D.﹣2x﹣1≤3
9.(2分)已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b
B.a+2>b+2
C.﹣a<﹣b
D.2a>3b
10.(2分)笔记本4元/本,钢笔5元/支,某同学购买笔记本和钢笔恰好用去162元,那么最多购买钢笔( )支.
A.28
B.29
C.30
D.31
二、准确填空.(本大题10个小题,每小题3分,共30分)
11.(3分)若方程(m﹣4)x|m|﹣3=3yn+1+4是二元一次方程,则m=
,n=
.
12.(3分)已知x、y满足方程组,则x+y的值为
.
13.(3分)如图,直线AB和CD相交于O点,OM⊥AB,∠BOD:∠COM=1:3,则∠AOD的度数为
度.
14.(3分)如图,直线l1,l2被l3所截,下列条件:①∠1=∠2;②∠3=∠4;③l1∥l2,其中能判断AC∥BD的条件是
.
15.(3分)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,∠BCD=40°,则∠BED的度数为
.
16.(3分)如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=39°,则∠2的度数是
.
17.(3分)已知am=6,an=3,则am+n=
.
18.(3分)“x与5的差不小于x的3倍”用不等式表示为
.
19.(3分)若关于x的不等式的非负整数解只有3个,则m的取值范围是
.
20.(3分)因式分解:ax2﹣a=
.
三、解答题.(本大题7个小题,共70分)
21.(10分)一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
22.(10分)如图,∠AGF=∠ABC,∠1+∠2=180°,
(1)求证;BF∥DE.
(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数.
23.(10分)欢欢与乐乐两人共同计算(2x+a)(3x+b),欢欢抄错为(2x﹣a)(3x+b),得到的结果为6x2﹣13x+6;乐乐抄错为(2x+a)(x+b),得到的结果为2x2﹣x﹣6.
(1)式子中的a、b的值各是多少?
(2)请计算出原题的正确答案.
24.(10分)根据题意,完成下列问题.
(1)若2m=8,2n=32,求22m﹣n的值;
(2)已知2x+3y﹣3=0,求4x?8y的值;
(3)已知2x+2?5x+2=103x﹣3,求x的值.
25.(10分)如图所示,AD⊥BC,EF⊥BC,∠BEF=∠ADG.试说明DG∥AB.把说明的过程填写完整.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°(
),
∴EF∥AD(
),
∴∠BEF=
( 两直线平行,同位角相等 ).
∵∠BEF=∠ADG(已知),
∴
(等量代换).
∴DG∥AB(
).
26.(10分)关于x的不等式组.
(1)若不等式组的解集是1<x<2,求a的值;
(2)若不等式组无解,求a的取值范围.
27.(10分)(1)简便计算:992﹣108×92;
(2)因式分解:2x3﹣8x2+8x.
2020-2021学年河北省沧州市任丘市七年级(下)期末数学试卷
参考答案与试题解析
一、正确选择.(本大题10个小题,每小题2分,共20分)
1.(2分)关于x,y的方程组的解为( )
A.
B.
C.
D.
【分析】利用加减消元法求解即可.
【解答】解:,
①﹣②,得x=﹣4,
把x=﹣4代入②,得﹣4+y=3,解得y=7.
故方程组的解为.
故选:A.
2.(2分)下列命题是真命题的( )
A.两点之间直线最短
B.如果ab>0,那么a>0,b>0
C.内错角相等,两直线平行
D.若|a|=1,则a=1
【分析】利用线段的性质、不等式的性质、平行线的判定及绝对值的意义分别判断后即可确定正确的选项.
【解答】解:A、两点之间线段最短,故原命题错误,是假命题,不符合题意;
B、如果ab>0,那么a>0,b>0或a<0,b<0,故原命题错误,是假命题,不符合题意;
C、内错角相等,两直线平行,正确,是真命题,符合题意;
D、若|a|=1,则a=±1,故原命题错误,是假命题,不符合题意,
故选:C.
3.(2分)如图,AB∥CD,点O在AB上,OE平分∠BOD,若∠CDO=100°,则∠BOE的度数为( )
A.30°
B.40°
C.50°
D.60°
【分析】根据平行线的性质可得∠BOD=100°,利用角平分线的性质可得∠BOE=50°.
【解答】解:∵AB∥CD,∠CDO=100°,
∴∠BOD=100°,
∵OE平分∠BOD,
∴∠BOE=50°.
故选:C.
4.(2分)已知三条线段长分别为2cm、4cm、acm,若这三条线段首尾顺次联结能围成一个三角形,那么a的取值可以是( )
A.1cm
B.2cm
C.4cm
D.7cm
【分析】根据三角形的三边关系确定a的取值范围即可求解.
【解答】解:依题意有4﹣2<a<4+2,
解得:2<a<6.
只有选项C在范围内.
故选:C.
5.(2分)下列现象中,( )是平移.
A.“天问”探测器绕火星运动
B.篮球在空中飞行
C.电梯的上下移动
D.将一张纸对折
【分析】要根据平移的性质,判断是否是平移现象,平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形).
【解答】解:A.“天问”探测器绕火星运动不是平移;
B.篮球在空中飞行不是平移;
C.电梯的上下移动是平移;
D.将一张纸对折不是平移;
故选:C.
6.(2分)据国家邮政局统计,2021年农历除夕和初一两天,全国快递处理超130
000
000件,与去年同期相比增长223%,快递的春节“不打烊”服务确保了广大用户能够顺利收到年货,欢度佳节.将130
000
000用科学记数法表示应为( )
A.1.3×107
B.13×107
C.1.3×108
D.0.13×109
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:130000000=1.3×108.
故选:C.
7.(2分)下列运算中,正确的是( )
A.a5+a5=a10
B.3a3?2a2=6a6
C.a6÷a2=a3
D.(﹣3ab)2=9a2b2
【分析】根据同底数幂的乘除法,幂的乘方与积的乘方的计算方法逐项计算即可.
【解答】解:A.a5+a5=2a5,因此选项A不符合题意;
B.3a3?2a2=6a5,因此选项B不符合题意;
C.a6÷a2=a4,因此选项C不符合题意;
D.(﹣3ab)2=9a2b2,因此选项D符合题意;
故选:D.
8.(2分)下列关系式中,不含有x=﹣1这个解的是( )
A.2x+1=﹣1
B.2x+1>﹣1
C.﹣2x+1≥3
D.﹣2x﹣1≤3
【分析】把x=﹣1代入各个不等式,满足不等式成立时,它就是该不等式的解.
【解答】解:当x=﹣1时,2x+1=﹣1,﹣2x+1=3≥3,﹣2x﹣1=1≤3,
所以x=﹣1满足选项A、C、D,因为﹣1不大于﹣1,所以x=﹣1不满足B.
故选:B.
9.(2分)已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b
B.a+2>b+2
C.﹣a<﹣b
D.2a>3b
【分析】根据不等式的性质即可得到a>b,a+2>b+2,﹣a<﹣b.
【解答】解:由不等式的性质得a>b,a+2>b+2,﹣a<﹣b.
故选:D.
10.(2分)笔记本4元/本,钢笔5元/支,某同学购买笔记本和钢笔恰好用去162元,那么最多购买钢笔( )支.
A.28
B.29
C.30
D.31
【分析】设该同学购买钢笔x支,笔记本y本,根据总价=单价×数量,即可得出关于x,y的二元一次方程,结合x,y均为正整数,即可得出各购买方案,取x的最大值即可得出结论.
【解答】解:设该同学购买钢笔x支,笔记本y本,
依题意得:5x+4y=162.
∵x,y均为正整数,
∴或或或或或或或,
∴x的最大值为30.
故选:C.
二、准确填空.(本大题10个小题,每小题3分,共30分)
11.(3分)若方程(m﹣4)x|m|﹣3=3yn+1+4是二元一次方程,则m= ﹣4 ,n= 0 .
【分析】二元一次方程就是只含有两个未知数,并且未知数的项的次数是1的整式方程,依据定义即可求解.
【解答】解:根据题意,得
|m|﹣3=1且n+1=1且m﹣4≠0,
解得m=﹣4,n=0.
故答案为:﹣4,0.
12.(3分)已知x、y满足方程组,则x+y的值为
5 .
【分析】将两式相加即可.
【解答】解:两式相加得3x+3y=15,
x+y=5.
故答案为:5.
13.(3分)如图,直线AB和CD相交于O点,OM⊥AB,∠BOD:∠COM=1:3,则∠AOD的度数为 157.5 度.
【分析】先根据OM⊥AB,得∠BOM=90°,再∠BOD:∠COM=1:3,可求出∠DOB,再根据平角关系,即可得出∠AOD的度数.
【解答】解:∵OM⊥AB,
∴∠BOM=90°,
∴∠BOD+∠COM=90°,
∵∠BOD:∠COM=1:3,
∴∠BOD=22.5°,
∵∠AOB=180°,
∴∠AOD=∠AOB﹣∠BOD=157.5°.
故答案为:157.5.
14.(3分)如图,直线l1,l2被l3所截,下列条件:①∠1=∠2;②∠3=∠4;③l1∥l2,其中能判断AC∥BD的条件是
① .
【分析】根据同位角相等,两直线平行即可判断AC∥BD.
【解答】解:①∵∠1=∠2,
∴AC∥BD(同位角相等,两直线平行).
故答案为:①.
15.(3分)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,∠BCD=40°,则∠BED的度数为 60° .
【分析】先根据角平分线的定义,得出∠ABE=∠CBE=∠ABC,∠ADE=∠CDE=∠ADC,再根据三角形内角和定理,推理得出∠BAD+∠BCD=2∠E,进而求得∠E的度数.
【解答】解:∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠CBE=∠ABC,∠ADE=∠CDE=∠ADC,
∵∠ABE+∠BAD=∠E+∠ADE,∠BCD+∠CDE=∠E+∠CBE,
∴∠ABE+∠BAD+∠BCD+∠CDE=∠E+∠ADE+∠E+∠CBE,
∴∠BAD+∠BCD=2∠E,
∵∠BAD=80°,∠BCD=40°,
∴∠E=(∠BAD+∠BCD)=(80°+40°)=60°.
故答案为:60°.
16.(3分)如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=39°,则∠2的度数是
21° .
【分析】过B作BC∥l1,可得∠2=∠ABC,由平行公理可得BC∥l2,根据平行线的性质可得∠1+∠2=∠ABD,结合直角三角板的特性可求解.
【解答】解:如图,过B作BC∥l1,
∴∠2=∠ABC,
∵l2∥l1,
∴BC∥l2,
∴∠CBD=∠1,
∴∠1+∠2=∠ABC+∠CBD=∠ABD,
由题意知:∠ABD=60°,
∴∠1+∠2=60°,
∵∠1=39°,
∴∠2=60°﹣39°=21°,
故答案为21°.
17.(3分)已知am=6,an=3,则am+n= 18 .
【分析】根据同底数幂的乘法底数不变指数相加,可得答案.
【解答】解:am+n=am?an=6×3=18,
故答案为:18.
18.(3分)“x与5的差不小于x的3倍”用不等式表示为
x﹣5≥3x .
【分析】根据x与5的差不小于x的3倍,可知x与5的差大于等于x的3倍,从而可以用相应的不等式表示出来.
【解答】解:“x与5的差不小于x的3倍”用不等式表示为x﹣5≥3x,
故答案为:x﹣5≥3x.
19.(3分)若关于x的不等式的非负整数解只有3个,则m的取值范围是
<m≤1 .
【分析】首先确定不等式组的解集,先利用含m的式子表示,根据非负整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于m的不等式,从而求出m的范围.
【解答】解:解不等式,得:x<3m,
∵关于x的不等式的非负整数解只有3个,
∴不等式的非负整数解为0、1、2,
则2<3m≤3,
解得:<m≤1,
故答案为:<m≤1.
20.(3分)因式分解:ax2﹣a= a(x+1)(x﹣1) .
【分析】首先提公因式a,再利用平方差进行二次分解即可.
【解答】解:原式=a(x2﹣1)=a(x+1)(x﹣1).
故答案为:a(x+1)(x﹣1).
三、解答题.(本大题7个小题,共70分)
21.(10分)一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
【分析】(1)设甲组工作一天商店应付x元,乙组工作一天商店应付y元,根据“若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据所需总费用=每天应付钱数×工作天数,分别求出单独请甲、乙两组完成所需费用,比较后即可得出结论;
(3)根据损失总钱数=每天盈利×装修时间+装修队所需费用,分别求出单独请甲、乙两组及请甲乙两组同时完成所损失的总钱数,比较后即可得出结论.
【解答】解:(1)设甲组工作一天商店应付x元,乙组工作一天商店应付y元,
根据题意得:,
解得:.
答:甲组工作一天商店应付300元,乙组工作一天商店应付140元.
(2)单独请甲组所需费用为:300×12=3600(元),
单独请乙组所需费用为:140×24=3360(元),
∵3600>3360,
∴单独请乙组所需费用最少.
(3)商店请甲乙两组同时装修,才更有利,理由如下:
单独请甲组完成,损失钱数为:200×12+3600=6000(元),
单独请乙组完成,损失钱数为:200×24+3360=8160(元),
请甲乙两组同时完成,损失钱数为:200×8+3520=5120(元).
∵8160>6000>5120,
∴商店请甲乙两组同时装修,才更有利.
22.(10分)如图,∠AGF=∠ABC,∠1+∠2=180°,
(1)求证;BF∥DE.
(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数.
【分析】(1)根据∠AGF=∠ABC可得出BC∥GF,进而可得出∠AFG=∠C,再根据角的计算可得出∠1=∠CDE,由此即可得出∠CED=∠CFB,根据“同位角相等,两直线平行”即可得出BF∥DE;
(2)根据DE⊥AC、BF∥DE即可得出∠AFB=90°,再结合∠1+∠2=180°、∠2=150°以及∠AFB=∠AFG+∠1即可算出∠AFG的度数.
【解答】(1)证明:∵∠AGF=∠ABC,
∴BC∥GF,
∴∠AFG=∠C.
∵∠1+∠2=180°,∠CDE+∠2=180°,
∴∠1=∠CDE.
∵∠CED=180°﹣∠C﹣∠CDE,∠CFB=180°﹣∠AFD﹣∠1,
∴∠CED=∠CFB,
∴BF∥DE.
(2)解:∵DE⊥AC,BF∥DE,
∴∠AFB=∠AED=90°,
∵∠1+∠2=180°,∠2=150°,
∴∠1=30°.
∵∠AFB=∠AFG+∠1=90°,
∴∠AFG=60°.
23.(10分)欢欢与乐乐两人共同计算(2x+a)(3x+b),欢欢抄错为(2x﹣a)(3x+b),得到的结果为6x2﹣13x+6;乐乐抄错为(2x+a)(x+b),得到的结果为2x2﹣x﹣6.
(1)式子中的a、b的值各是多少?
(2)请计算出原题的正确答案.
【分析】(1)根据由于欢欢抄错了第一个多项式中的a符号,得出的结果为6x2﹣13x+6,可知(2x﹣a)(3x+b)=6x2+(2b﹣3a)x﹣ab=6x2﹣13x+6,于是2b﹣3a=﹣13①;再根据乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2﹣x﹣6,可知常数项是﹣6,可知(2x+a)(x+b)=2x2﹣x﹣6,可得到2b+a=﹣1②,解关于①②的方程组即可求出a、b的值;
(2)把a、b的值代入原式求出整式乘法的正确结果.
【解答】解:(1)根据题意可知,由于欢欢抄错了第一个多项式中的a的符号,得到的结果为6x2﹣13x+6,
那么(2x﹣a)(3x+b)=6x2+(2b﹣3a)x﹣ab=6x2﹣13x+6,
可得2b﹣3a=﹣13
①
乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2﹣x﹣6,
可知(2x+a)(x+b)=2x2﹣x﹣6
即2x2+(2b+a)x+ab=2x2﹣x﹣6,
可得2b+a=﹣1
②,
解关于①②的方程组,可得a=3,b=﹣2;
(2)正确的式子:
(2x+3)(3x﹣2)=6x2+5x﹣6
24.(10分)根据题意,完成下列问题.
(1)若2m=8,2n=32,求22m﹣n的值;
(2)已知2x+3y﹣3=0,求4x?8y的值;
(3)已知2x+2?5x+2=103x﹣3,求x的值.
【分析】(1)直接利用同底数幂的除法运算法则以及幂的乘方运算法则将原式变形,进而得出答案;
(2)直接利用同底数幂的乘法运算法则以及幂的乘方运算法则将原式变形进,而得出答案;
(3)直接利用同底数幂的乘法运算法则以及积的乘方运算法则将原式变形进,而得出答案.
【解答】解:(1)∵2m=8,2n=32,
∴22m﹣n=(2m)2÷2n=82÷32=64÷32=2;
∴22m﹣n的值为2;
(2)∵2x+3y﹣3=0,
∴2x+3y=3,
∴4x?8y=22x?23y=22x+3y=23=8;
∴4x?8y的值为8;
(3)∵2x+2?5x+2=10x+2,
∴10x+2=103x﹣3,
∴x+2=3x﹣3,
∴,
∴x的值为.
25.(10分)如图所示,AD⊥BC,EF⊥BC,∠BEF=∠ADG.试说明DG∥AB.把说明的过程填写完整.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°(
垂直的定义 ),
∴EF∥AD(
同位角相等,两直线平行 ),
∴∠BEF= ∠BAD ( 两直线平行,同位角相等 ).
∵∠BEF=∠ADG(已知),
∴ ∠ADG=∠BAD (等量代换).
∴DG∥AB(
内错角相等,两直线平行 ).
【分析】根据垂直的定义得出∠EFB=∠ADB=90°,即可判定EF∥AD,则得出∠BEF=∠BAD,等量代换得出∠ADG=∠BAD,即可判定DG∥AB.
【解答】解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°(垂直的定义),
∴EF∥AD(同位角相等,两直线平行),
∴∠BEF=∠BAD(两直线平行,同位角相等),
∵∠BEF=∠ADG(已知),
∴∠ADG=∠BAD(等量代换),
∴DG∥AB(内错角相等,两直线平行).
故答案为:垂直的定义;同位角相等,两直线平行;∠BAD;∠ADG=∠BAD;内错角相等,两直线平行.
26.(10分)关于x的不等式组.
(1)若不等式组的解集是1<x<2,求a的值;
(2)若不等式组无解,求a的取值范围.
【分析】(1)解不等式组中两个不等式后根据不等式组的解集可得关于a的方程,解之可得;
(2)根据“大小小大无解了”可确定关于a的不等式,解之可得.
【解答】解:(1)解不等式2x+1>3得:x>1,
解不等式a﹣x>1得:x<a﹣1,
∵不等式组的解集是1<x<2,
∴a﹣1=2,
解得:a=3;
(2)∵不等式组无解,
∴a﹣1≤1,
解得:a≤2.
27.(10分)(1)简便计算:992﹣108×92;
(2)因式分解:2x3﹣8x2+8x.
【分析】(1)把992﹣108×92写成(100﹣1)2﹣(100+8)(100﹣)的形式,再利用完全平方公式和平方差进行计算即可.
(2)首先提取公因式2x,再进一步运用完全平方公式计算即可解答.
【解答】解:(1)992﹣108×92
=(100﹣1)2﹣(100+8)(100﹣8)
=1002﹣200+1﹣1002+82
=﹣200+1+64
=﹣135;
(2)原式=2x(x2﹣4x+4)
=2x(x﹣2)2.
同课章节目录
