3.4二次函数y=ax^2+bx+c的图象与性质 课件(共40张)
文档属性
| 名称 | 3.4二次函数y=ax^2+bx+c的图象与性质 课件(共40张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 00:00:00 | ||
图片预览









文档简介
(共43张PPT)
第三章
二次函数
4
二次函数y=ax2+bx+c的图象与性质
知识点一
二次函数y=ax2+k(a≠0)的图象与性质
二次函数y=ax2+k(a≠0)的图象是一条抛物线,它的称轴是y轴,顶点坐标是(O,k),是由抛物线y=ax向上或向下平移|k|个单位得到的.
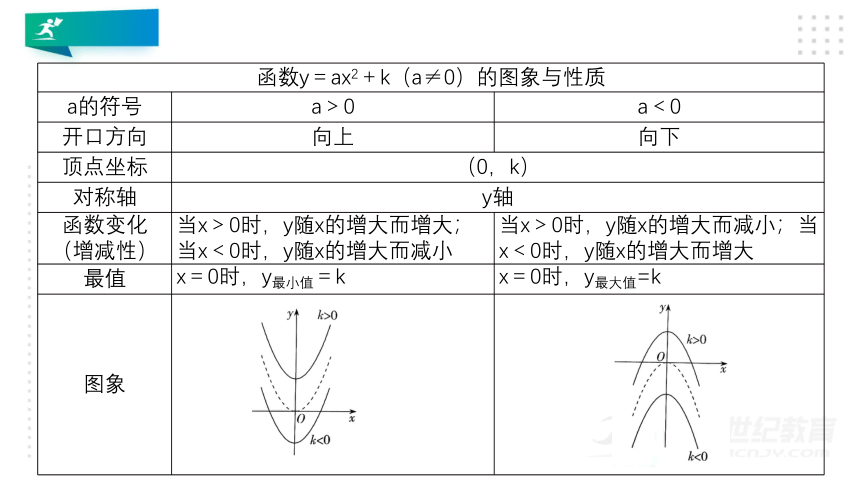
函数y=ax2+k(a≠0)的图象与性质
a的符号
a>0
a<0
开口方向
向上
向下
顶点坐标
(0,k)
对称轴
y轴
函数变化(增减性)
当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小
当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大
最值
x=0时,y最小值=k
x=0时,y最大值=k
图象
例1
已知抛物线的解析式为y=-2x2+1,则抛物线的顶点坐标为____________.
例1
已知抛物线的解析式为y=-2x2+1,则抛物线的顶点坐标为____________.
解析
抛物线y=-2x2+1关于y轴对称,当x=0时,y=1.
∴抛物线的顶点坐标为(0,1).
例1
已知抛物线的解析式为y=-2x2+1,则抛物线的顶点坐标为____________.
解析
抛物线y=-2x2+1关于y轴对称,当x=0时,y=1.
∴抛物线的顶点坐标为(0,1).
答案
(0,1)
知识点二
二次函数y=a(x-h)2(a≠0)的图象与性质
二次函数y=a(x-h)2(a≠0)的图象是一条抛物线,它对称轴是平行于y轴或与y轴重合的直线x=h,顶点坐(h,0),是由抛物线y=ax2向右或向左平移h个单位到的.
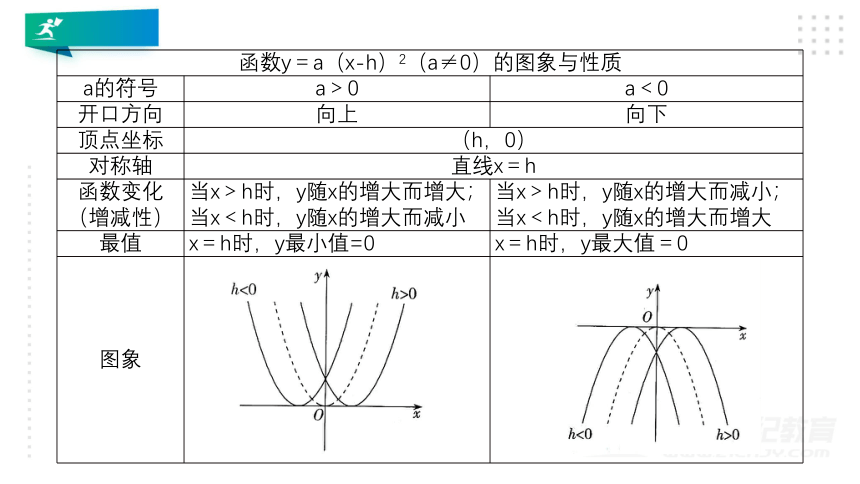
函数y=a(x-h)2(a≠0)的图象与性质
a的符号
a>0
a<0
开口方向
向上
向下
顶点坐标
(h,0)
对称轴
直线x=h
函数变化(增减性)
当x>h时,y随x的增大而增大;当x<h时,y随x的增大而减小
当x>h时,y随x的增大而减小;当x<h时,y随x的增大而增大
最值
x=h时,y最小值=0
x=h时,y最大值=0
图象
例2
已知抛物线y=-3(x+2)2,当x_________时,y随x的增大而增大;当x________时,y随x的增大而减小.
例2
已知抛物线y=-3(x+2)2,当x_________时,y随x的增大而增大;当x________时,y随x的增大而减小.
解析
抛物线y=-3(x+2)2的开口向下,顶点坐标为(-2,0),
所以当x<-2时,y随x的增大而增大;
当x>-2时,y随x的增大而减小.
例2
已知抛物线y=-3(x+2)2,当x_________时,y随x的增大而增大;当x________时,y随x的增大而减小.
解析
抛物线y=-3(x+2)2的开口向下,顶点坐标为(-2,0),
所以当x<-2时,y随x的增大而增大;
当x>-2时,y随x的增大而减小.
答案
<-2;>-2
知识点三
二次函数y=a(x-h)2+k(a≠0)的图象与性质
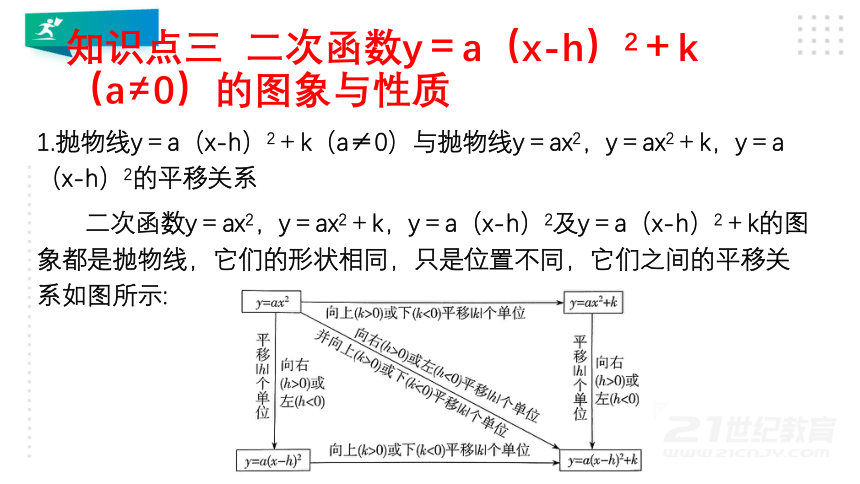
1.抛物线y=a(x-h)2+k(a≠0)与抛物线y=ax2,y=ax2+k,y=a(x-h)2的平移关系
二次函数y=ax2,y=ax2+k,y=a(x-h)2及y=a(x-h)2+k的图象都是抛物线,它们的形状相同,只是位置不同,它们之间的平移关系如图所示:
2.抛物线y=a(x-h)2+k(a≠0)的平移规律
移动方向(m>0)
平移前的解析式
平移后的解析式
简记
向左平移m个单位
y=a(x-h)2+k
y=a(x-h+m)2+k
左加
向右平移m个单位
y=a(x-h)2+k
y=a(x-h-m)2+k
右减
向上平移m个单位
y=a(x-h)2+k
y=a(x-h)2+k+m
上加
向下平移m个单位
y=a(x-h)2+k
y=a(x-h)2+k-m
下减
抛物线的平移口诀:自变量加减左右移,函数值加减上下移.
温馨提示
①抛物线在平移的过程中,a的值不发生变化.
②涉及抛物线的平移时,首先将表达式转化为顶点式y=a(x-h)2+k的形式.
③抛物线的移动主要看顶点的移动,抛物线y=ax2的顶点是(0,0),抛物线y=ax2+k的顶点是(0,k),抛物线y=a(x-h)2的顶点是(h,0),抛物线y=a(x-h)2+k的顶点是(h,k).我们只需在坐标系中画出这几个顶点,即可轻松地看出平移的方向.
例3
将抛物线y=(x+2)2先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的表达式为(
)
A.y=(x+3)2-2
B.y=(x+3)2+2
C.y=(x+1)2+2
D.y=(x+1)2-2
例3
将抛物线y=(x+2)2先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的表达式为(
)
A.y=(x+3)2-2
B.y=(x+3)2+2
C.y=(x+1)2+2
D.y=(x+1)2-2
解析
方法一:抛物线y=(x+2)2的顶点坐标是(-2,0),先向右平移1个单位长度,再向上平移2个单位长度,顶点坐标变为(-1,2),所以平移后抛物线的表达式为y=(x+1)2+2.
方法二:将抛物线y=(x+2)2先向右平移1个单位长度,得到抛物线y=(x+2-1)2=(x+1)2,再向上平移2个单位长度,得到的抛物线的表达式为y=(x+1)2+2.
方法归纳
解决抛物线的平移问题一般有两种解决方法,一是将问题转化为顶点的平移问题解决;二是直接利用抛物线的平移规律“左加右减,上加下减”解决.
3.二次函数y=a(x-h)2+k(a≠0)的图象与性质
图象
性质(增减性)
y=a(x-h)2+k的图象与性质
开口方向
对称轴
顶点坐标
x取哪些值时,y的值随x值的增大而增大
x取哪些值时,y的值随x值的增大而减小
a>0
向上
直线x=h
(h,k)
x>h
xa<0
向下
xx>h
知识点四
二次函数y=ax2+bx+c(a≠0)图象与性质
1.二次函数y=ax2+bx+c(a≠0)的配方
步骤如下:
(1)将二次项及一次项作为一组,一起放在括号里;
(2)对于括号里的部分,提出二次项的系数,将二次项的系数化为1;
(3)将括号里的部分配方;
(4)整理,并化为y=a(x-h)2+k的形式.
特别提醒
二次函数解析式的配方同一元二次方程的配方的区别:
(1)二次函数解析式的配方是恒等变形,不能将二次项的系数约去,只能提出来;
(2)一元二次方程的配方是同解变形.
一般地,二次函数y=ax2+bx+c(a≠0)有以下性质:
y=ax2+bx+c的性质
x取哪些值时,y的值随x值的增大而增大
x取哪些值时,y的值随x值的增大而减小
最值
a>0
有最小值,且y最小值=
a<0
有最大值,且y最大值=
二次函数y=ax2+bx+c(a≠0)的图象与系数的关系如下表所示:
规律总结
a决定形状
a的符号决定开口方向
a>0,开口向上
a<0,开口向下
a的绝对值决定开口大小
绝对值越大,开口越小
绝对值越小,开口越大
a、b
决定对称轴的位置
对称轴是直线
当b=0时,对称轴为y轴
当a,b同号时,对称轴在y轴左侧
当a,b异号时,对称轴在y轴右侧
c决定上下位置
抛物线与y轴交于点(0,c)
当c>0时,抛物线与y轴交于正半轴
当c=0时,抛物线经过原点
当c<0时,抛物线与y轴交于负半轴
方法归纳
3.二次函数y=ax2+bx+c(a≠0)的图象的画法
一般方法:列表、描点、连线
简易画法:五点定形法
步骤:
(1)先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点M,并用虚线画出对称轴.
(2)求抛物线y=ax2+bx+c与坐标轴的交点.
当抛物线与x轴有两个交点A,B时,描出这两个交点及抛物线与y轴的交点C,再找到点C关于对称轴的对称点D,将A,B,C,D及M这五个点按从左到右的顺序连接起来.
当抛物线与x轴只有一个交点或无交点时,描出抛物线与y轴的交点C及其关于对称轴的对称点D,由C,M,D三点可粗略地画出二次函数图象的草图.如果需要画出比较精确的图象,可再描出一对对称点A,B,然后用光滑曲线顺次连接上述五点,即可画出二次函数的图象.
经典例题
题型一
根据二次函数的图象判断各项系数及其间关系
例1
已知二次函数y=ax2+bx+c图象的对称轴为x=1,其图象如图所示,现有下列结论:①abc>0,②b-2a<0,③a-b+c>0,④a+b>n(an+b)(n≠1),⑤2c<3b.其中正确的是(
)
A.①③
B.②⑤
C.③④
D.④⑤
方法技巧
解此类题常用到的技巧有:
①利用二次函数的图象与系数的关系,判断系数的正负,进而判断它们的积或商的正负;
②利用抛物线的对称轴,判断a,b的数量关系;
③利用抛物线的对称性比较两点纵坐标的大小,已知点坐标,求它关于对称轴对称的点的坐标;
④利用特殊点,得到关于系数的等式或不等式,进而利用等式或不等式的性质经过变形解决问题,如当x=1,-1,2,-2时,y的值分别等于a+b+c,a-b+c,4a+2b+c,4a-2b+c;若x=1,y=0,则得等式a+b+c=0,若x=2,y<0,则得不等式4a+2b+c<0,等等;
⑤综合②④,得到关于a,c或b,c的关系式;
⑥若需要判断含有am2+bm(m在自变量的取值范围内)的式子的大小,则往往需要借助于顶点或特殊点的纵坐标进行比较.
题型二
二次函数图象与性质的简单应用
例2
如图所示,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间的函数关系式为y=-5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15m时,飞行的时间是多少?
(2)在飞行过程中,小球从飞出到落地所用的时间是多少?
(3)在飞行过程中,小球的飞行高度何时最大?最大高度是多少?
解析(1)当y=15时,15=-5x2+20x,解得x1=1,x2=3.
答:在飞行过程中,当小球的飞行高度为15m时,飞行的时间是1s或3s.
(2)当y=0时,0=-5x2+20x,解得x1=0(舍),x2=4.
答:在飞行过程中,小球从飞出到落地所用的时间是4s.
(3)y=-5x2+20x=-5(x-2)2+20,
∴当x=2时,y取得最大值,此时y最大值=20.
答:在飞行过程中,小球的飞行高度在第2s时最大,最大高度是20m.
解析(1)当y=15时,15=-5x2+20x,解得x1=1,x2=3.
答:在飞行过程中,当小球的飞行高度为15m时,飞行的时间是1s或3s.
(2)当y=0时,0=-5x2+20x,解得x1=0(舍),x2=4.
答:在飞行过程中,小球从飞出到落地所用的时间是4s.
(3)y=-5x2+20x=-5(x-2)2+20,
∴当x=2时,y取得最大值,此时y最大值=20.
答:在飞行过程中,小球的飞行高度在第2s时最大,最大高度是20m.
归纳总结
解决此类问题的关键是将实际问题转化为二次函数的图象与性质问题这里第(1)问注意对应同一高度的时间有两个值.
易错易混
易错点
混淆抛物线的平移规律
图形平移问题一般转化为点的平移问题解决,抛物线的平移也不例外若是利用抛物线的平移规律判断,要明确:y的值与变化的数值在等号(抛物线的解析式)两侧,因此上加下减,与平移规律一致;x的值与变化的数值在等号同侧,因此左加右减,与平移规律相反.
例
将抛物线y=2(x-3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是(
)
A.y=2(x-6)2
B.y=2(x-6)2+4
C.y=2x2
D.y=2x2+4
例
将抛物线y=2(x-3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是(
)
A.y=2(x-6)2
B.y=2(x-6)2+4
C.y=2x2
D.y=2x2+4
解析
将抛物线y=2(x-3)2+2向左平移3个单位长度所得抛物线解析式为y=2(x-3+3)2+2,即y=2x2+2;再向下平移2个单位长度得到的抛物线的解析式为y=2x2+2-2,即y=2x2.故选C.
例
将抛物线y=2(x-3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是(
)
A.y=2(x-6)2
B.y=2(x-6)2+4
C.y=2x2
D.y=2x2+4
解析
将抛物线y=2(x-3)2+2向左平移3个单位长度所得抛物线解析式为y=2(x-3+3)2+2,即y=2x2+2;再向下平移2个单位长度得到的抛物线的解析式为y=2x2+2-2,即y=2x2.故选C.
易错警示
注意抛物线的平移规律与一般图形平移规律的区别,不要混淆.
第三章
二次函数
4
二次函数y=ax2+bx+c的图象与性质
知识点一
二次函数y=ax2+k(a≠0)的图象与性质
二次函数y=ax2+k(a≠0)的图象是一条抛物线,它的称轴是y轴,顶点坐标是(O,k),是由抛物线y=ax向上或向下平移|k|个单位得到的.
函数y=ax2+k(a≠0)的图象与性质
a的符号
a>0
a<0
开口方向
向上
向下
顶点坐标
(0,k)
对称轴
y轴
函数变化(增减性)
当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小
当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大
最值
x=0时,y最小值=k
x=0时,y最大值=k
图象
例1
已知抛物线的解析式为y=-2x2+1,则抛物线的顶点坐标为____________.
例1
已知抛物线的解析式为y=-2x2+1,则抛物线的顶点坐标为____________.
解析
抛物线y=-2x2+1关于y轴对称,当x=0时,y=1.
∴抛物线的顶点坐标为(0,1).
例1
已知抛物线的解析式为y=-2x2+1,则抛物线的顶点坐标为____________.
解析
抛物线y=-2x2+1关于y轴对称,当x=0时,y=1.
∴抛物线的顶点坐标为(0,1).
答案
(0,1)
知识点二
二次函数y=a(x-h)2(a≠0)的图象与性质
二次函数y=a(x-h)2(a≠0)的图象是一条抛物线,它对称轴是平行于y轴或与y轴重合的直线x=h,顶点坐(h,0),是由抛物线y=ax2向右或向左平移h个单位到的.
函数y=a(x-h)2(a≠0)的图象与性质
a的符号
a>0
a<0
开口方向
向上
向下
顶点坐标
(h,0)
对称轴
直线x=h
函数变化(增减性)
当x>h时,y随x的增大而增大;当x<h时,y随x的增大而减小
当x>h时,y随x的增大而减小;当x<h时,y随x的增大而增大
最值
x=h时,y最小值=0
x=h时,y最大值=0
图象
例2
已知抛物线y=-3(x+2)2,当x_________时,y随x的增大而增大;当x________时,y随x的增大而减小.
例2
已知抛物线y=-3(x+2)2,当x_________时,y随x的增大而增大;当x________时,y随x的增大而减小.
解析
抛物线y=-3(x+2)2的开口向下,顶点坐标为(-2,0),
所以当x<-2时,y随x的增大而增大;
当x>-2时,y随x的增大而减小.
例2
已知抛物线y=-3(x+2)2,当x_________时,y随x的增大而增大;当x________时,y随x的增大而减小.
解析
抛物线y=-3(x+2)2的开口向下,顶点坐标为(-2,0),
所以当x<-2时,y随x的增大而增大;
当x>-2时,y随x的增大而减小.
答案
<-2;>-2
知识点三
二次函数y=a(x-h)2+k(a≠0)的图象与性质
1.抛物线y=a(x-h)2+k(a≠0)与抛物线y=ax2,y=ax2+k,y=a(x-h)2的平移关系
二次函数y=ax2,y=ax2+k,y=a(x-h)2及y=a(x-h)2+k的图象都是抛物线,它们的形状相同,只是位置不同,它们之间的平移关系如图所示:
2.抛物线y=a(x-h)2+k(a≠0)的平移规律
移动方向(m>0)
平移前的解析式
平移后的解析式
简记
向左平移m个单位
y=a(x-h)2+k
y=a(x-h+m)2+k
左加
向右平移m个单位
y=a(x-h)2+k
y=a(x-h-m)2+k
右减
向上平移m个单位
y=a(x-h)2+k
y=a(x-h)2+k+m
上加
向下平移m个单位
y=a(x-h)2+k
y=a(x-h)2+k-m
下减
抛物线的平移口诀:自变量加减左右移,函数值加减上下移.
温馨提示
①抛物线在平移的过程中,a的值不发生变化.
②涉及抛物线的平移时,首先将表达式转化为顶点式y=a(x-h)2+k的形式.
③抛物线的移动主要看顶点的移动,抛物线y=ax2的顶点是(0,0),抛物线y=ax2+k的顶点是(0,k),抛物线y=a(x-h)2的顶点是(h,0),抛物线y=a(x-h)2+k的顶点是(h,k).我们只需在坐标系中画出这几个顶点,即可轻松地看出平移的方向.
例3
将抛物线y=(x+2)2先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的表达式为(
)
A.y=(x+3)2-2
B.y=(x+3)2+2
C.y=(x+1)2+2
D.y=(x+1)2-2
例3
将抛物线y=(x+2)2先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的表达式为(
)
A.y=(x+3)2-2
B.y=(x+3)2+2
C.y=(x+1)2+2
D.y=(x+1)2-2
解析
方法一:抛物线y=(x+2)2的顶点坐标是(-2,0),先向右平移1个单位长度,再向上平移2个单位长度,顶点坐标变为(-1,2),所以平移后抛物线的表达式为y=(x+1)2+2.
方法二:将抛物线y=(x+2)2先向右平移1个单位长度,得到抛物线y=(x+2-1)2=(x+1)2,再向上平移2个单位长度,得到的抛物线的表达式为y=(x+1)2+2.
方法归纳
解决抛物线的平移问题一般有两种解决方法,一是将问题转化为顶点的平移问题解决;二是直接利用抛物线的平移规律“左加右减,上加下减”解决.
3.二次函数y=a(x-h)2+k(a≠0)的图象与性质
图象
性质(增减性)
y=a(x-h)2+k的图象与性质
开口方向
对称轴
顶点坐标
x取哪些值时,y的值随x值的增大而增大
x取哪些值时,y的值随x值的增大而减小
a>0
向上
直线x=h
(h,k)
x>h
x
向下
x
知识点四
二次函数y=ax2+bx+c(a≠0)图象与性质
1.二次函数y=ax2+bx+c(a≠0)的配方
步骤如下:
(1)将二次项及一次项作为一组,一起放在括号里;
(2)对于括号里的部分,提出二次项的系数,将二次项的系数化为1;
(3)将括号里的部分配方;
(4)整理,并化为y=a(x-h)2+k的形式.
特别提醒
二次函数解析式的配方同一元二次方程的配方的区别:
(1)二次函数解析式的配方是恒等变形,不能将二次项的系数约去,只能提出来;
(2)一元二次方程的配方是同解变形.
一般地,二次函数y=ax2+bx+c(a≠0)有以下性质:
y=ax2+bx+c的性质
x取哪些值时,y的值随x值的增大而增大
x取哪些值时,y的值随x值的增大而减小
最值
a>0
有最小值,且y最小值=
a<0
有最大值,且y最大值=
二次函数y=ax2+bx+c(a≠0)的图象与系数的关系如下表所示:
规律总结
a决定形状
a的符号决定开口方向
a>0,开口向上
a<0,开口向下
a的绝对值决定开口大小
绝对值越大,开口越小
绝对值越小,开口越大
a、b
决定对称轴的位置
对称轴是直线
当b=0时,对称轴为y轴
当a,b同号时,对称轴在y轴左侧
当a,b异号时,对称轴在y轴右侧
c决定上下位置
抛物线与y轴交于点(0,c)
当c>0时,抛物线与y轴交于正半轴
当c=0时,抛物线经过原点
当c<0时,抛物线与y轴交于负半轴
方法归纳
3.二次函数y=ax2+bx+c(a≠0)的图象的画法
一般方法:列表、描点、连线
简易画法:五点定形法
步骤:
(1)先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点M,并用虚线画出对称轴.
(2)求抛物线y=ax2+bx+c与坐标轴的交点.
当抛物线与x轴有两个交点A,B时,描出这两个交点及抛物线与y轴的交点C,再找到点C关于对称轴的对称点D,将A,B,C,D及M这五个点按从左到右的顺序连接起来.
当抛物线与x轴只有一个交点或无交点时,描出抛物线与y轴的交点C及其关于对称轴的对称点D,由C,M,D三点可粗略地画出二次函数图象的草图.如果需要画出比较精确的图象,可再描出一对对称点A,B,然后用光滑曲线顺次连接上述五点,即可画出二次函数的图象.
经典例题
题型一
根据二次函数的图象判断各项系数及其间关系
例1
已知二次函数y=ax2+bx+c图象的对称轴为x=1,其图象如图所示,现有下列结论:①abc>0,②b-2a<0,③a-b+c>0,④a+b>n(an+b)(n≠1),⑤2c<3b.其中正确的是(
)
A.①③
B.②⑤
C.③④
D.④⑤
方法技巧
解此类题常用到的技巧有:
①利用二次函数的图象与系数的关系,判断系数的正负,进而判断它们的积或商的正负;
②利用抛物线的对称轴,判断a,b的数量关系;
③利用抛物线的对称性比较两点纵坐标的大小,已知点坐标,求它关于对称轴对称的点的坐标;
④利用特殊点,得到关于系数的等式或不等式,进而利用等式或不等式的性质经过变形解决问题,如当x=1,-1,2,-2时,y的值分别等于a+b+c,a-b+c,4a+2b+c,4a-2b+c;若x=1,y=0,则得等式a+b+c=0,若x=2,y<0,则得不等式4a+2b+c<0,等等;
⑤综合②④,得到关于a,c或b,c的关系式;
⑥若需要判断含有am2+bm(m在自变量的取值范围内)的式子的大小,则往往需要借助于顶点或特殊点的纵坐标进行比较.
题型二
二次函数图象与性质的简单应用
例2
如图所示,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间的函数关系式为y=-5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15m时,飞行的时间是多少?
(2)在飞行过程中,小球从飞出到落地所用的时间是多少?
(3)在飞行过程中,小球的飞行高度何时最大?最大高度是多少?
解析(1)当y=15时,15=-5x2+20x,解得x1=1,x2=3.
答:在飞行过程中,当小球的飞行高度为15m时,飞行的时间是1s或3s.
(2)当y=0时,0=-5x2+20x,解得x1=0(舍),x2=4.
答:在飞行过程中,小球从飞出到落地所用的时间是4s.
(3)y=-5x2+20x=-5(x-2)2+20,
∴当x=2时,y取得最大值,此时y最大值=20.
答:在飞行过程中,小球的飞行高度在第2s时最大,最大高度是20m.
解析(1)当y=15时,15=-5x2+20x,解得x1=1,x2=3.
答:在飞行过程中,当小球的飞行高度为15m时,飞行的时间是1s或3s.
(2)当y=0时,0=-5x2+20x,解得x1=0(舍),x2=4.
答:在飞行过程中,小球从飞出到落地所用的时间是4s.
(3)y=-5x2+20x=-5(x-2)2+20,
∴当x=2时,y取得最大值,此时y最大值=20.
答:在飞行过程中,小球的飞行高度在第2s时最大,最大高度是20m.
归纳总结
解决此类问题的关键是将实际问题转化为二次函数的图象与性质问题这里第(1)问注意对应同一高度的时间有两个值.
易错易混
易错点
混淆抛物线的平移规律
图形平移问题一般转化为点的平移问题解决,抛物线的平移也不例外若是利用抛物线的平移规律判断,要明确:y的值与变化的数值在等号(抛物线的解析式)两侧,因此上加下减,与平移规律一致;x的值与变化的数值在等号同侧,因此左加右减,与平移规律相反.
例
将抛物线y=2(x-3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是(
)
A.y=2(x-6)2
B.y=2(x-6)2+4
C.y=2x2
D.y=2x2+4
例
将抛物线y=2(x-3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是(
)
A.y=2(x-6)2
B.y=2(x-6)2+4
C.y=2x2
D.y=2x2+4
解析
将抛物线y=2(x-3)2+2向左平移3个单位长度所得抛物线解析式为y=2(x-3+3)2+2,即y=2x2+2;再向下平移2个单位长度得到的抛物线的解析式为y=2x2+2-2,即y=2x2.故选C.
例
将抛物线y=2(x-3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是(
)
A.y=2(x-6)2
B.y=2(x-6)2+4
C.y=2x2
D.y=2x2+4
解析
将抛物线y=2(x-3)2+2向左平移3个单位长度所得抛物线解析式为y=2(x-3+3)2+2,即y=2x2+2;再向下平移2个单位长度得到的抛物线的解析式为y=2x2+2-2,即y=2x2.故选C.
易错警示
注意抛物线的平移规律与一般图形平移规律的区别,不要混淆.
