人教版六年级上册数学 4.3《比的应用》课件(共20张PPT)
文档属性
| 名称 | 人教版六年级上册数学 4.3《比的应用》课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 10:28:49 | ||
图片预览






文档简介
(共20张PPT)
4.3《比的应用》
速答
2.某班有男生18人,女生14人,男生和女生人数的比是多少?
3.学校体育组买来三种球,其中篮球5个,足球4个,排球8个。
(1)买来篮球、足球和排球的个数比是多少?
(2)买来的篮球的个数占三种球总数的几分之几?
(3)买来的足球的个数占三种球总数的几分之几?
(4)买来的排球的个数占三种球总数的几分之几?
复习回顾
1.200kg的 是多少千克?
1
4
同学们,随着科技的发展,农业上各种防止病虫害和增产增收的药剂、生活中的清洁剂、消毒液等使用前都要加水按一定的比稀释后才能使用,叫稀释液。按什么比加以稀释呢?厂家在药瓶使用说明上已经标注。请同学们看一组药剂使用说明,找到稀释比。
朗读清丽小诗
喜雨降临五月初,唤醒种子欲破土。
农家无眠早早起,笑看妻儿背药壶。
激情生趣
仔细阅读瓶上的使用说明,就能找到配制浓度。
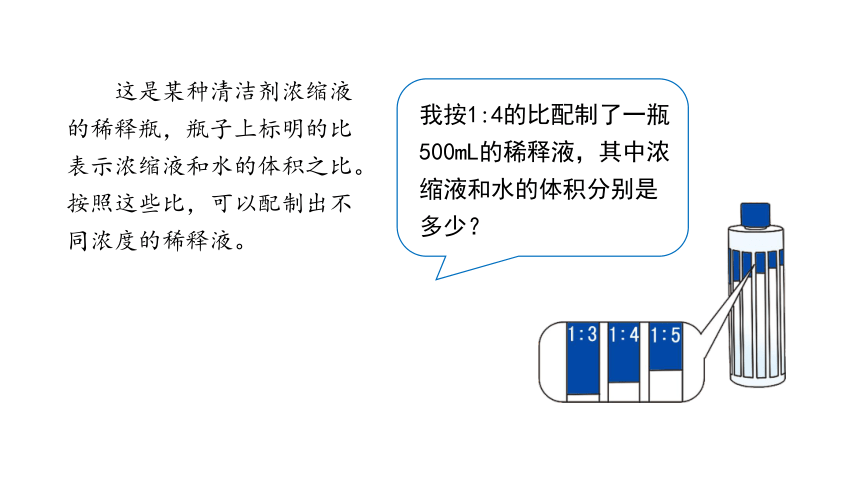
我按1:4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
按例2给的条件和问题,整理成一道应用题。
在例2中500ml是谁的体积?是按什么比配制的?稀释液中包含哪两个量?1:4是哪两个量的比?稀释液总份数是多少?这两个量的体积分别占总体积的几分之几?
书中用哪两种方法求浓缩液和水的体积?自己尝试算一算。
合作学习,学会配制
自学提纲
2.
1.
3.
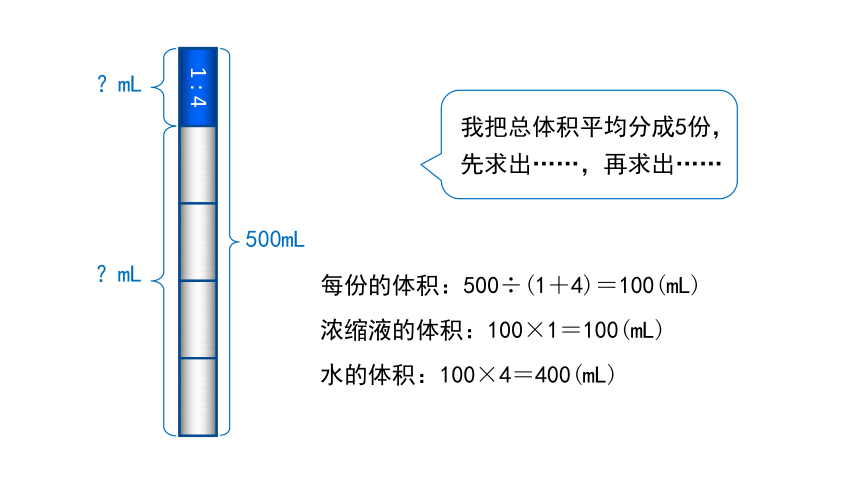
我把总体积平均分成5份,先求出……,再求出……
500mL
?mL
1 : 4
每份的体积:500÷(1+4)=100(mL)
浓缩液的体积:100×1=100(mL)
水的体积:100×4=400(mL)
?mL
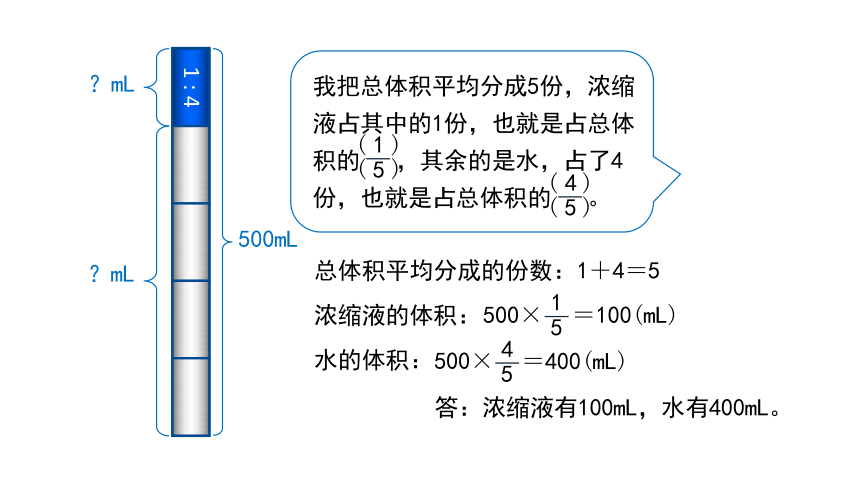
我把总体积平均分成5份,浓缩液占其中的1份,也就是占总体积的 ,其余的是水,占了4份,也就是占总体积的 。
( )
( )
( )
( )
500mL
?mL
1 : 4
总体积平均分成的份数:1+4=5
浓缩液的体积:
水的体积:
答:浓缩液有100mL,水有400mL。
5
1
5
4
500×
=100(mL)
5
1
500×
=400(mL)
5
4
?mL
结构特征:
已知总数和各部分数的比,求各部分数。
方法与步骤:
1.根据比先求出总份数。
2.求出各部分数占总数的几分之几。
3.运用分数乘法列式计算,求出各部分数。
4.答题并检验。
总结
某妇产医院上月新生婴儿303名,男女婴儿人数之比是51:50。上月新生男、女婴儿各有多少人?
新生婴儿平均分成的份数:51+50=101
新生男婴儿的人数:
新生女婴儿的人数:
答:上月新生男婴儿有153人,新生女婴儿有150人。
303×
101
51
=153(人)
303×
101
50
=150(人)
巩固练习
教材第55页练习十二第1题。
1.
教材第55页练习十二第2题。
答:需要蜂蜜20mL,水180mL。
9+1=10
200× =20(mL)
1
10
1+9=10
200× =180(mL)
9
10
200÷10=20(mL)
20×1=20(mL)
20×9=180(mL)
方法二:
方法一:
巩固练习
可以用1份蜂蜜
和9份水来冲兑
蜂蜜水。
这个杯子的容积正好是200mL,要冲兑一满杯这样的蜂蜜水,需要蜂蜜和水各多少毫升?
方法二:
方法一:
用120cm的铁丝做一个长方体的框架。长、宽、高的比是3:2:1。这个长方体的长、宽、高分别是多少?
答:这个长方体的长、宽、高分别是15cm、10cm、5cm。
30× =15(cm)
3
6
3+2+1=6
30× =10(cm)
2
6
30÷6=5(cm)
5×3=15(cm)
5×2=10(cm)
120÷4=30
5×1=5(cm)
3+2+1=6
120÷4=30
30× =5(cm)
1
6
拓展提高
按比分配这类题关键要识别:
(1)给出的比是哪两种量?例如:水和浓缩液的比,水和药液(总数)的比,
浓缩液和药液的比……
(2)识别给出的数量是总数还是其中一个量,再确定解法。例如下列题:
1.浓缩液2毫升,浓缩液和水的比是1:500。
(1)求需要水多少毫升。
(2)能配制这样的药液多少毫升?
2.浓缩液和水的比是1:500,水比浓缩液多499毫升,能配制这样的药液多少毫升?
温馨提示
这节课你学到了什么知识?有什么收获?
填一填。
(1)如果把3∶7的前项加9,要使它的比值不变,后项应加( )。
(2)学校合唱队女生人数是男生的1.5倍,女生人数和男生人数的最简整数比是( ),男生人数和合唱队总人数的最简整数比是( )。
21
3∶2
2∶5
(3)如图,甲与乙的最简整数比是( ),乙与丙的最简整数比是( ),丙与甲的比值是( )。
3∶4
4∶5
谁投球的命中率高一些?用我们学过的比的知识说一说理由。
右面四个情境中的比,可以用2∶3表示的有几个?
可以用2∶3表示的有1个。
阳阳和多多都喜欢集邮,他们的邮票枚数的比是7∶5,已知阳阳的邮票比多多多20枚。他们两人各有多少枚邮票?
7-5=2 20÷2=10(枚) 10×7=70(枚) 10×5=50(枚)
答:阳阳有70枚邮票,多多有50枚邮票。
布置作业
1.教材55页3、4题。
2.教材56页7题。
4.3《比的应用》
速答
2.某班有男生18人,女生14人,男生和女生人数的比是多少?
3.学校体育组买来三种球,其中篮球5个,足球4个,排球8个。
(1)买来篮球、足球和排球的个数比是多少?
(2)买来的篮球的个数占三种球总数的几分之几?
(3)买来的足球的个数占三种球总数的几分之几?
(4)买来的排球的个数占三种球总数的几分之几?
复习回顾
1.200kg的 是多少千克?
1
4
同学们,随着科技的发展,农业上各种防止病虫害和增产增收的药剂、生活中的清洁剂、消毒液等使用前都要加水按一定的比稀释后才能使用,叫稀释液。按什么比加以稀释呢?厂家在药瓶使用说明上已经标注。请同学们看一组药剂使用说明,找到稀释比。
朗读清丽小诗
喜雨降临五月初,唤醒种子欲破土。
农家无眠早早起,笑看妻儿背药壶。
激情生趣
仔细阅读瓶上的使用说明,就能找到配制浓度。
我按1:4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
按例2给的条件和问题,整理成一道应用题。
在例2中500ml是谁的体积?是按什么比配制的?稀释液中包含哪两个量?1:4是哪两个量的比?稀释液总份数是多少?这两个量的体积分别占总体积的几分之几?
书中用哪两种方法求浓缩液和水的体积?自己尝试算一算。
合作学习,学会配制
自学提纲
2.
1.
3.
我把总体积平均分成5份,先求出……,再求出……
500mL
?mL
1 : 4
每份的体积:500÷(1+4)=100(mL)
浓缩液的体积:100×1=100(mL)
水的体积:100×4=400(mL)
?mL
我把总体积平均分成5份,浓缩液占其中的1份,也就是占总体积的 ,其余的是水,占了4份,也就是占总体积的 。
( )
( )
( )
( )
500mL
?mL
1 : 4
总体积平均分成的份数:1+4=5
浓缩液的体积:
水的体积:
答:浓缩液有100mL,水有400mL。
5
1
5
4
500×
=100(mL)
5
1
500×
=400(mL)
5
4
?mL
结构特征:
已知总数和各部分数的比,求各部分数。
方法与步骤:
1.根据比先求出总份数。
2.求出各部分数占总数的几分之几。
3.运用分数乘法列式计算,求出各部分数。
4.答题并检验。
总结
某妇产医院上月新生婴儿303名,男女婴儿人数之比是51:50。上月新生男、女婴儿各有多少人?
新生婴儿平均分成的份数:51+50=101
新生男婴儿的人数:
新生女婴儿的人数:
答:上月新生男婴儿有153人,新生女婴儿有150人。
303×
101
51
=153(人)
303×
101
50
=150(人)
巩固练习
教材第55页练习十二第1题。
1.
教材第55页练习十二第2题。
答:需要蜂蜜20mL,水180mL。
9+1=10
200× =20(mL)
1
10
1+9=10
200× =180(mL)
9
10
200÷10=20(mL)
20×1=20(mL)
20×9=180(mL)
方法二:
方法一:
巩固练习
可以用1份蜂蜜
和9份水来冲兑
蜂蜜水。
这个杯子的容积正好是200mL,要冲兑一满杯这样的蜂蜜水,需要蜂蜜和水各多少毫升?
方法二:
方法一:
用120cm的铁丝做一个长方体的框架。长、宽、高的比是3:2:1。这个长方体的长、宽、高分别是多少?
答:这个长方体的长、宽、高分别是15cm、10cm、5cm。
30× =15(cm)
3
6
3+2+1=6
30× =10(cm)
2
6
30÷6=5(cm)
5×3=15(cm)
5×2=10(cm)
120÷4=30
5×1=5(cm)
3+2+1=6
120÷4=30
30× =5(cm)
1
6
拓展提高
按比分配这类题关键要识别:
(1)给出的比是哪两种量?例如:水和浓缩液的比,水和药液(总数)的比,
浓缩液和药液的比……
(2)识别给出的数量是总数还是其中一个量,再确定解法。例如下列题:
1.浓缩液2毫升,浓缩液和水的比是1:500。
(1)求需要水多少毫升。
(2)能配制这样的药液多少毫升?
2.浓缩液和水的比是1:500,水比浓缩液多499毫升,能配制这样的药液多少毫升?
温馨提示
这节课你学到了什么知识?有什么收获?
填一填。
(1)如果把3∶7的前项加9,要使它的比值不变,后项应加( )。
(2)学校合唱队女生人数是男生的1.5倍,女生人数和男生人数的最简整数比是( ),男生人数和合唱队总人数的最简整数比是( )。
21
3∶2
2∶5
(3)如图,甲与乙的最简整数比是( ),乙与丙的最简整数比是( ),丙与甲的比值是( )。
3∶4
4∶5
谁投球的命中率高一些?用我们学过的比的知识说一说理由。
右面四个情境中的比,可以用2∶3表示的有几个?
可以用2∶3表示的有1个。
阳阳和多多都喜欢集邮,他们的邮票枚数的比是7∶5,已知阳阳的邮票比多多多20枚。他们两人各有多少枚邮票?
7-5=2 20÷2=10(枚) 10×7=70(枚) 10×5=50(枚)
答:阳阳有70枚邮票,多多有50枚邮票。
布置作业
1.教材55页3、4题。
2.教材56页7题。
