冀教版九上数学 23.1.3 求平均数的应用 课件(共17张PPT)
文档属性
| 名称 | 冀教版九上数学 23.1.3 求平均数的应用 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 08:31:25 | ||
图片预览





文档简介
(共17张PPT)
23.1
平均数与加权平均数
第3课时
求平均数的应用
第23章
数据分析
类型
权为百分比的加权平均数的应用
1
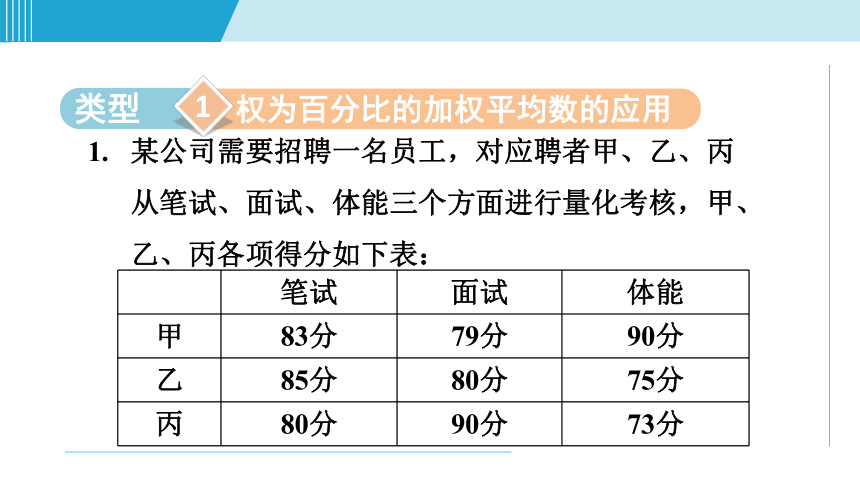
某公司需要招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,甲、乙、丙各项得分如下表:
?
笔试
面试
体能
甲
83分
79分
90分
乙
85分
80分
75分
丙
80分
90分
73分
(1)根据三项得分的平均分,从高到低确定三名
应聘者的排名顺序;
(2)该公司规定:笔试、面试、体能得分分别不得低
于80分、80分、70分,并按60%,30%,10%的
比例计入总分,根据规定,请你说明谁将被录用.
(1)x甲=(83+79+90)÷3=84(分),
x乙=(85+80+75)÷3=80(分),
x丙=(80+90+73)÷3=81(分).
从高到低确定三名应聘者的排名顺序为甲、丙、乙.
解:
(2)因为该公司规定:笔试、面试、体能得分分别不
得低于80分、80分、70分,所以甲被淘汰.
乙成绩为85×60%+80×30%+75×10%=82.5(分),
丙成绩为80×60%+90×30%+73×10%=82.3(分),
故乙将被录用.
类型
权为整数比的加权平均数的应用
2
2.某单位需招聘一名技术员,对甲、乙、丙三名候
选人进行了笔试和面试两项测试,其成绩如下表
所示,根据录用程序,该单位又组织了100名评议
人员对三人进行投票测评,三人得票率如扇形统
计图所示,每票1分.
(没有弃权票,每人只能投1票)
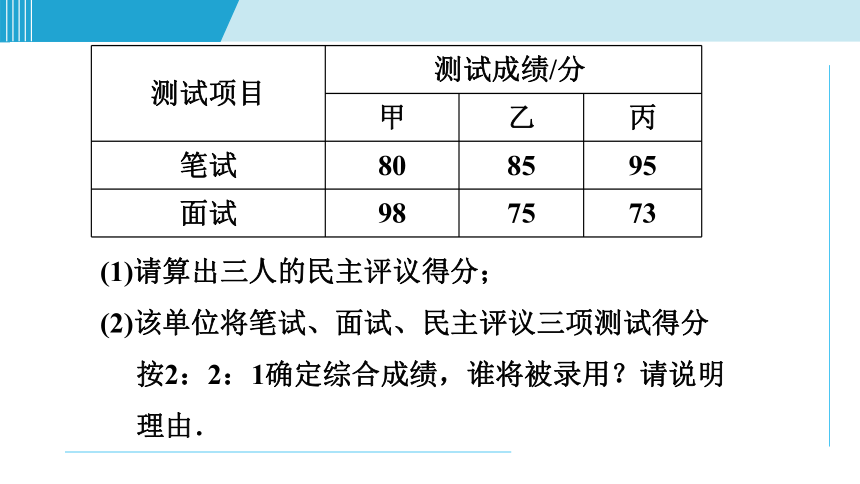
(1)请算出三人的民主评议得分;
(2)该单位将笔试、面试、民主评议三项测试得分
按2:2:1确定综合成绩,谁将被录用?请说明
理由.
测试项目
?测试成绩/分??
甲
乙
丙
笔试
80
85
95
面试
98
75
73
(1)甲民主评议得分:100×25%=25(分);乙民主评
议得分:100×40%=40(分);丙民主评议得分:
100×35%=35(分).
(2)甲将被录用.理由:
甲的成绩:
乙的成绩:
丙的成绩:
因为甲的成绩最好,所以甲将被录用.
解:
类型
权为频数的加权平均数的应用
3
3.为了了解某县八年级女生的身高情况,在该县某
校八年级女生中随机抽测了200名,身高的统计数据如下:
组别
身高x/cm
人数
第一组
135≤x<145
50
第二组
145≤x<155
P
第三组
155≤x<165
70
第四组
165≤x<175
Q
类型
解法提醒:
借助频数统计图(表)中的组中值计算加权平均
数的一般步骤:
1.
计算每个小组的组中值.
2.
以每个小组的组中值作为各组的代表值,
对应的频数作为“权”计算加权平均数.
请你结合所给数据,回答下列问题:
(1)表中的P=________,Q=________;
(2)请把如图所示的频数分布直方图补充完整;
(3)这200名女生的平均身高大约________.
解题秘方:(1)
由统计图可以看出:p=60,
则q=200-50-60-70=20.
(2)根据q=20
即可补全频数分布直方图.
(3)求出每组的组中值分别为140
cm,150
cm,160
cm,170
cm,
用每组的组中值近似地作为该组内女生的平均身高.
,
因此这200
名女生的平均身高大约为153
cm.
解:(1)60;20
(2)
(3)153cm
类型
权为组中值的加权平均数的应用
4
4.为了解某校九年级学生的体能,随机抽取部分学生进行1
min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理,下面是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成频数分布直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组的频率之和为0.12,且第②组与第⑥组的频数都是12;
丁:第②、③、④组的频数之比为4?17?15.
根据这四名同学提供的信息,请解答如下问题:
(1)这次跳绳测试共抽取学生多少名?各组有多少人?
(2)如果跳绳次数不少于135次为优秀,则这次跳绳测
试中达到优秀的人数为多少?
(3)以每组的组中值(每组
的中点对应的数据)作
为这组跳绳次数的代
表,估计这批学生
1
min跳绳次数的平均数.
(1)∵第①组的频率为1-96%=0.04,
∴第②组的频率为0.12-0.04=0.08,
则这次跳绳测试共抽取学生12÷0.08=150(名).
∴第①组的人数为150×0.04=6.
∵第②、③、④组的频数之比为4:17:15,
第②组的频数为12,
∴第③、④组的人数分别为51,45,则第⑤组的
人数为150-(6+12+51+45+12)=24.
∴第①~⑥组分别有6人、12人、51人、45人、
24
人、12人.
解:
(2)第⑤、⑥两组的频率之和为
=0.16+0.08=0.24,
∴150×0.24=36(人)达到优秀.
(3)估计这批学生1
min跳绳次数的平均数为
必做:
请完成教材课后习题
课后作业
作业
23.1
平均数与加权平均数
第3课时
求平均数的应用
第23章
数据分析
类型
权为百分比的加权平均数的应用
1
某公司需要招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,甲、乙、丙各项得分如下表:
?
笔试
面试
体能
甲
83分
79分
90分
乙
85分
80分
75分
丙
80分
90分
73分
(1)根据三项得分的平均分,从高到低确定三名
应聘者的排名顺序;
(2)该公司规定:笔试、面试、体能得分分别不得低
于80分、80分、70分,并按60%,30%,10%的
比例计入总分,根据规定,请你说明谁将被录用.
(1)x甲=(83+79+90)÷3=84(分),
x乙=(85+80+75)÷3=80(分),
x丙=(80+90+73)÷3=81(分).
从高到低确定三名应聘者的排名顺序为甲、丙、乙.
解:
(2)因为该公司规定:笔试、面试、体能得分分别不
得低于80分、80分、70分,所以甲被淘汰.
乙成绩为85×60%+80×30%+75×10%=82.5(分),
丙成绩为80×60%+90×30%+73×10%=82.3(分),
故乙将被录用.
类型
权为整数比的加权平均数的应用
2
2.某单位需招聘一名技术员,对甲、乙、丙三名候
选人进行了笔试和面试两项测试,其成绩如下表
所示,根据录用程序,该单位又组织了100名评议
人员对三人进行投票测评,三人得票率如扇形统
计图所示,每票1分.
(没有弃权票,每人只能投1票)
(1)请算出三人的民主评议得分;
(2)该单位将笔试、面试、民主评议三项测试得分
按2:2:1确定综合成绩,谁将被录用?请说明
理由.
测试项目
?测试成绩/分??
甲
乙
丙
笔试
80
85
95
面试
98
75
73
(1)甲民主评议得分:100×25%=25(分);乙民主评
议得分:100×40%=40(分);丙民主评议得分:
100×35%=35(分).
(2)甲将被录用.理由:
甲的成绩:
乙的成绩:
丙的成绩:
因为甲的成绩最好,所以甲将被录用.
解:
类型
权为频数的加权平均数的应用
3
3.为了了解某县八年级女生的身高情况,在该县某
校八年级女生中随机抽测了200名,身高的统计数据如下:
组别
身高x/cm
人数
第一组
135≤x<145
50
第二组
145≤x<155
P
第三组
155≤x<165
70
第四组
165≤x<175
Q
类型
解法提醒:
借助频数统计图(表)中的组中值计算加权平均
数的一般步骤:
1.
计算每个小组的组中值.
2.
以每个小组的组中值作为各组的代表值,
对应的频数作为“权”计算加权平均数.
请你结合所给数据,回答下列问题:
(1)表中的P=________,Q=________;
(2)请把如图所示的频数分布直方图补充完整;
(3)这200名女生的平均身高大约________.
解题秘方:(1)
由统计图可以看出:p=60,
则q=200-50-60-70=20.
(2)根据q=20
即可补全频数分布直方图.
(3)求出每组的组中值分别为140
cm,150
cm,160
cm,170
cm,
用每组的组中值近似地作为该组内女生的平均身高.
,
因此这200
名女生的平均身高大约为153
cm.
解:(1)60;20
(2)
(3)153cm
类型
权为组中值的加权平均数的应用
4
4.为了解某校九年级学生的体能,随机抽取部分学生进行1
min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理,下面是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成频数分布直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组的频率之和为0.12,且第②组与第⑥组的频数都是12;
丁:第②、③、④组的频数之比为4?17?15.
根据这四名同学提供的信息,请解答如下问题:
(1)这次跳绳测试共抽取学生多少名?各组有多少人?
(2)如果跳绳次数不少于135次为优秀,则这次跳绳测
试中达到优秀的人数为多少?
(3)以每组的组中值(每组
的中点对应的数据)作
为这组跳绳次数的代
表,估计这批学生
1
min跳绳次数的平均数.
(1)∵第①组的频率为1-96%=0.04,
∴第②组的频率为0.12-0.04=0.08,
则这次跳绳测试共抽取学生12÷0.08=150(名).
∴第①组的人数为150×0.04=6.
∵第②、③、④组的频数之比为4:17:15,
第②组的频数为12,
∴第③、④组的人数分别为51,45,则第⑤组的
人数为150-(6+12+51+45+12)=24.
∴第①~⑥组分别有6人、12人、51人、45人、
24
人、12人.
解:
(2)第⑤、⑥两组的频率之和为
=0.16+0.08=0.24,
∴150×0.24=36(人)达到优秀.
(3)估计这批学生1
min跳绳次数的平均数为
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
