3.5确定二次函数的表达式 同步练习(含答案)
文档属性
| 名称 | 3.5确定二次函数的表达式 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 15:00:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章
二次函数
5
确定二次函数的表达式
知识能力全练
知识点一
设一般式确定二次函数的表达式
1.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不煳”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”p与加工煎炸时间t(单位:分钟)近似满足的函数关系为p=at2+bt+c(a≠0,a,b,c是常数),如下图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为(
)
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
2.2022年冬季奥运会将在北京举行,为迎接比赛,某滑雪运动员从山坡滑下,测得滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系可以近似地用二次函数来表示,现测得一组数据,如下表所示,则二次函数的表达式为_________________.
滑行时间t/s
0
1
2
3
…
滑行距离s/m
0
5
14
27
…
3.已知一条抛物线过(-2,6),(2,-4),(3,1)三点,求这条抛物线的表达式.
4.已知某抛物线与抛物线y=-3x2+2x-5的形状和开口方向均相同,且过点A(1,2),B(4,5).
(1)求此抛物线的表达式;
(2)用配方法求此抛物线的顶点坐标.
5.如图所示,已知抛物线y=ax2+2ax+c(a<0)与x轴的交点为A(-3,0)和B,与y轴的交点为C,若∠ACO=∠CBO,试求抛物线的表达式.
知识点二
设顶点式确定二次函数的表达式
6.已知图象的顶点坐标为(-2,1),且经过原点的二次函数的表达式是(
)
A.y=(x-2)2+1
B.y=-(x+2)2+1
C.y=(x+2)2+1
D.y=(x-2)2+1
7.二次函数的部分图象如图所示,对称轴是直线x=-1,则这个二次函数的表达式为(
)
A.y=-x2+2x+3
B.y=x2+2x+3
C.y=-x2+2x-3
D.y=-x2-2x+3
8.如图所示,隧道的截面由抛物线和长方形构成.长方形的长为12
m,宽为5
m,抛物线的最高点C离路面AA1的距离为8
m,过AA1的中点O建立如图所示的直角坐标系,则该抛物线的函数表达式为_____________.
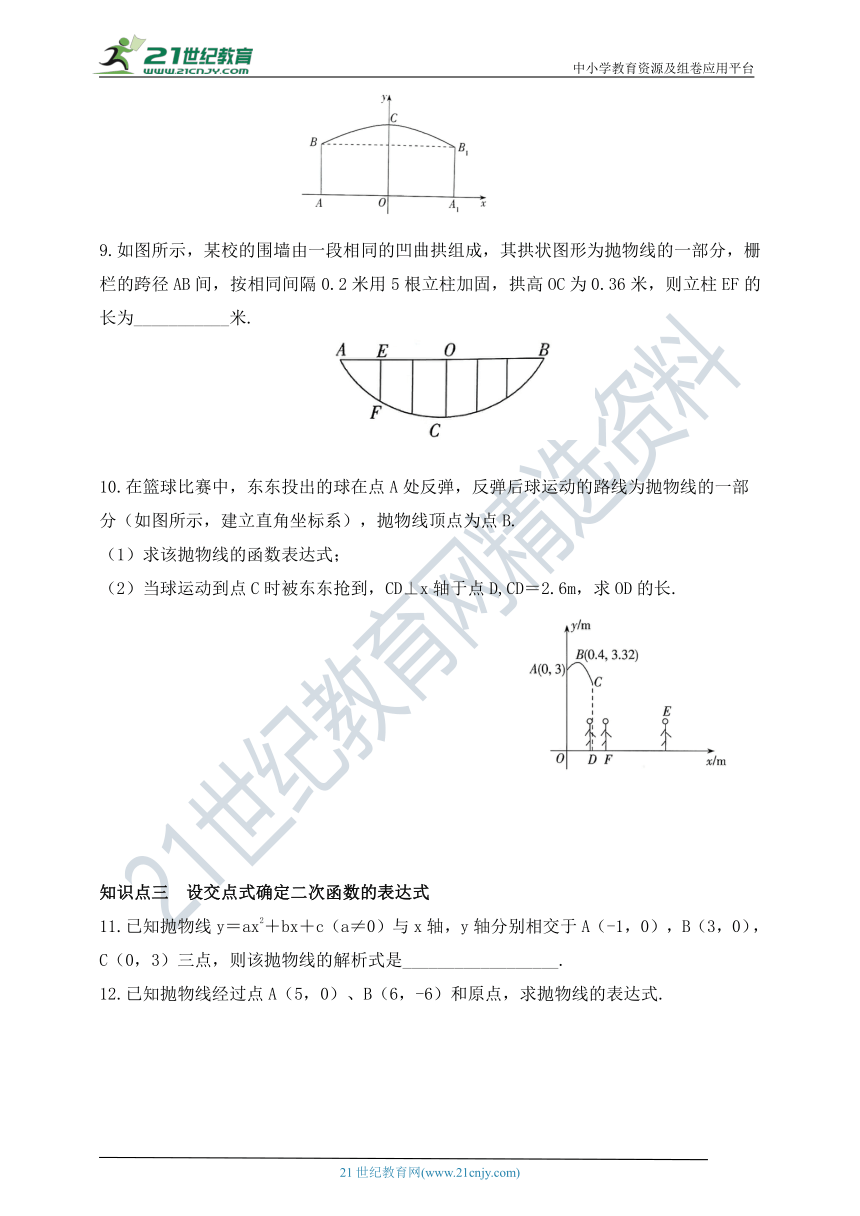
9.如图所示,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB间,按相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为___________米.
10.在篮球比赛中,东东投出的球在点A处反弹,反弹后球运动的路线为抛物线的一部
分(如图所示,建立直角坐标系),抛物线顶点为点B.
(1)求该抛物线的函数表达式;
(2)当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m,求OD的长.
知识点三
设交点式确定二次函数的表达式
11.已知抛物线y=ax2+bx+c(a≠0)与x轴,y轴分别相交于A(-1,0),B(3,0),C(0,3)三点,则该抛物线的解析式是__________________.
12.已知抛物线经过点A(5,0)、B(6,-6)和原点,求抛物线的表达式.
13.如图所示,在平面直角坐标系中抛物线y=x2+bx+c与x轴交于点A(3,0),点B(-1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)过点D(0,3)作直线MN∥x轴,点P在直线MN上且S△PAC=S△DBC,求点P的坐标.
巩固提高全练
14.如图①,单孔拱桥的形状近似抛物线形,建立如图②所示的平面直角坐标系,在正常水位时,水面宽度OA为12m,拱桥的最高点B到水面OA的距离为6m,则抛物线的解析式为________________.
15.如图所示,在平面直角坐标系中,抛物线y=ax2+bx-2交x轴于A,B两点,交y轴于点C,且OA=2OC=8OB.点P是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若PC∥AB,求点P的坐标.
16.如图所示,直线y=x+n与抛物线y=ax2+bx+5(a≠0)相交于A(1.2)和B(4,m)两点,点P是线段AB上异于A,B的动点,过点P作PD⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
17.已知抛物线y=ax2+bx+1经过点(1,-2),(-2,13).
(1)求a,b的值;
(2)若(5,y1).(m,y2)是抛物线上不同的两点,且y2=12-y1,求m的值.
18.如图所示,开口向下的抛物线与x轴交于点A(-1.0),B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
19.如图①,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线的绳子.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图②),使左边抛物线F1的最低点距MN
1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为.设MN离AB的距离为m,抛物线F2的顶点离地面的距离为k,当2≤k≤2.5时,求m的取值范围.
20.如图所示,抛物线y=ax2-3ax-4a经过点C(0,2),交x轴于点A、B(点A在点B左侧),连接BC,直线y=kx+1(k>0)与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.
(1)求抛物线的解析式及点A,B的坐标;
(2)是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.
参考答案
1.C
2.
3.解析
设抛物线的表达式为y=ax2+b+c(a≠0),将(-2,6),(2,-4),(3,1)分别代入,得,解得,
所以这条抛物线的表达式为.
4.解析
(1)∵某抛物线与抛物线y=-3x2+2x-5的形状和开口方向均相同,
∴设此抛物线的表达式为y=-3x2+bx+c,∵该抛物线过点A(1,2),B(4,5),
∴,解得,∴此抛物线的表达式y=-3x2+16x-11.
(2).
∴此抛物线的顶点坐标为.
5.解析
∵抛物线y=ax2+2ax+c的对称轴为直线x==-1,抛物线与x轴的交点为A(-3,0)和B,∴点B的坐标为(1,0).
∵∠ACO=∠CBO,∴tan∠ACO=tan∠CBO,即,即,OC=.
将A(-3,0),C(0,3)代入y=ax2+2ax+c,得,解得.
∴抛物线的表达式为.
6.B
7.D
8.
9.
0.2
10.解析
(1)设y=a(x-0.4)2+3.32(a≠0),
把x=0,y=3代入,得3=a(0-0.4)2+3.32.解得a=-2.
∴抛物线的函数表达式为y=-2(x-0.4)2+3.32.
(2)把y=2.6代入y=-2(x-0.4)2+3.32,得2.6=-2(x-0.4)2+3.32.
解得x1=-0.2(舍去),x2=1.∴0D的长为1
m.
y=-x2+2x+3
12.解析
因为抛物线经过点A(5,0)和原,所以设抛物线的表达式为y=ax(x-5)(a≠0)将B(6,6)代人,得-6=6a(6-5),解得a=-1.
所以抛物线的表达式为y=-x2+5x.
13.解析
(1)解法一:抛物线y=x2+bx+c点A(3,0),点B(-1,0),
∴y=(x-3)(x+1)=x2-2x-3.
解法二:将点A(3,0),点B(-1,0)代入y=x2+bx+c,
得,解得.∴y=x2-2x-3.
(2)易知点C的坐标为(0,-3),∴S△DBC=×6×1=3,∴S△PAC=3.
设P(x,3),直线CP与x轴的交点为Q,则S△PAC=×6×AQ,∴AQ=1,
∴点Q的坐标为(2,0)或(4,0),∴直线CQ的表达式为y=x-3或y=x-3,
当y=3时,x=4或x=8,∴点P的坐标为(4,3)或(8,3).
14.
15.解析
(1)把x=0代入y=ax2+bx-2,得y=-2,∴点C的坐标为(0,-2).
∵OA=20C=80B,∴点A的坐标为(-4,0),点B的坐标为.
设抛物线的表达式为y=a(x+4)(x-),
将点C(O,-2)代入,得-2=-2a.解得a=1.
故抛物线的表达式为y=(x+4)(x-)=x2+x-2.
(2)抛物线的对称轴为直线x=-.
当PC∥AB时,点P,C的纵坐标相同,点P的横坐标为-×2=-.
∴点P的坐标为(-,-2).
16.解析
(1)把A(1,2)代入y=x+n,得1+n=2.解得n=1.
∴一次函数的解析式为y=x+1.把B(4,m)代入y=x+1,得m=4+1=5.
∴B的坐标为(4,5).把A(1,2),B(4,5)代入y=ax2+bx+5,
得,解得,∴抛物线的解析式为y=x2-4x+5.
(2)存在设P的坐标为(t,t+1)(1<t<4).
∵PD⊥x轴,∴C的坐标为(t,t2-4t+5).
∴PC=t+1-(t2-4t+5)=-t2+5t-4=.
∴当t=时,PC的长有最大值,最大值为.
17.解析
(1)把点(1,-2),(-2,13)入y=ax2+bx+1,
得,解得.
(2)由(1)得函数解析式为y=x2-4x+1,把(5,y1)代入y=x2-4x+1,得y1=6.
∴y2=12-y1=6.∵y1=y2,抛物线的对称轴为直线x==2.∴m=2×2-5=-1.
18.解析
(1)∵A(-1,0),B(2,0),C(0,4),
∴设抛物线的解析式为y=a(x+1)(x-2),
将C(0,4)代入,得4=-2a.解得a=-2.
∴该抛物线的解析式为y=-2(x+1)(x-2)=-2x2+2x+4.
(2)如图,连接OP,设点P的坐标为(m,-2m2+2m+4)(0<m<2),
∵A(-1,0),B(2,0),C(0,4),∴OA=1,OC=4,0B=2.
∴S四边形CABP=S△OAC+S△OCP+S△OPB
=×1×4+×4m+×2×(-2m2+2m+4)=-2m2+4m+6=-2(m-1)2+8.
∴当m=1时,S的最大值为8.
19.解析
(1)∵a=>0,∴抛物线的顶点为最低点,
∴,∴绳子最低点离地面的距离为米.
(2)由(1)可知,BD=8,令x=0,得y=3,∴A(0,3),C(8,3).
由题意得,抛物线F1的顶点坐标为(2,1.8),设F1的解析式为y=a1(x-2)2+1.8(a1≠0),将(0,3)代入,得4a1+1.8=3解得a1=0.3,
∴抛物线F1的解析式为y=0.3(x-2)2+1.8.
当x=3时,y=0.3×1+1.8=2.1,∴MN的长度为2.1米.
(3)∵MN=CD=3,∴根据抛物线的对称性可知抛物线F2的顶点在线段ND的垂直平分线上,∴抛物线F2的顶点坐标为(m+4,k).∴抛物线F2的解析式为.
把C(8,3)代入,得,∴,∴.
∴k是关于m的二次函数.又∵m<8,∴k随m的增大而增大.
当k=2时,(m-8)2+3=2,解得m1=4,m2=12(不符合题意,舍去).
当k=2.5时,(m-8)2+3=2.5,解得m3=8-2,m4=8+2(不符合题意,舍去).∴m的取值范围是4≤m≤8-2.
20.解析
(1)把C(0,2)代入y=ax2-3ax-4a,得-4a=2解得a=-.
则抛物线的解析式为.
由于=-(x+1)(x-4).
故A的坐标为(-1,0),B的坐标为(4,0).
(2)存在理由如下:
由题意知,点E位于y轴右侧,作EG∥y轴,交BC于点G,如图.
∴CD∥EG.∴△CDF∽△GEF,∴.
∵直线y=kx+1(k>0)与y轴交于点D,∴D(0,1),
∴CD=2-1=1.∴.
设BC所在直线的解析式为y=mx+n(m≠0).
将B(4,0),C(0,2)代入,得,解得.
∴直线BC的解析式是y=-x+2.
设E(t,),则G(t,-t+2),其中0<t<4.
∴EG=()-(-t+2)=-(t-2)2+2.
∴.
∵,∴当t=2时,存在最大值,最大值为2,此时点E的坐标是(2,3).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第三章
二次函数
5
确定二次函数的表达式
知识能力全练
知识点一
设一般式确定二次函数的表达式
1.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不煳”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”p与加工煎炸时间t(单位:分钟)近似满足的函数关系为p=at2+bt+c(a≠0,a,b,c是常数),如下图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为(
)
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
2.2022年冬季奥运会将在北京举行,为迎接比赛,某滑雪运动员从山坡滑下,测得滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系可以近似地用二次函数来表示,现测得一组数据,如下表所示,则二次函数的表达式为_________________.
滑行时间t/s
0
1
2
3
…
滑行距离s/m
0
5
14
27
…
3.已知一条抛物线过(-2,6),(2,-4),(3,1)三点,求这条抛物线的表达式.
4.已知某抛物线与抛物线y=-3x2+2x-5的形状和开口方向均相同,且过点A(1,2),B(4,5).
(1)求此抛物线的表达式;
(2)用配方法求此抛物线的顶点坐标.
5.如图所示,已知抛物线y=ax2+2ax+c(a<0)与x轴的交点为A(-3,0)和B,与y轴的交点为C,若∠ACO=∠CBO,试求抛物线的表达式.
知识点二
设顶点式确定二次函数的表达式
6.已知图象的顶点坐标为(-2,1),且经过原点的二次函数的表达式是(
)
A.y=(x-2)2+1
B.y=-(x+2)2+1
C.y=(x+2)2+1
D.y=(x-2)2+1
7.二次函数的部分图象如图所示,对称轴是直线x=-1,则这个二次函数的表达式为(
)
A.y=-x2+2x+3
B.y=x2+2x+3
C.y=-x2+2x-3
D.y=-x2-2x+3
8.如图所示,隧道的截面由抛物线和长方形构成.长方形的长为12
m,宽为5
m,抛物线的最高点C离路面AA1的距离为8
m,过AA1的中点O建立如图所示的直角坐标系,则该抛物线的函数表达式为_____________.
9.如图所示,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB间,按相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为___________米.
10.在篮球比赛中,东东投出的球在点A处反弹,反弹后球运动的路线为抛物线的一部
分(如图所示,建立直角坐标系),抛物线顶点为点B.
(1)求该抛物线的函数表达式;
(2)当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m,求OD的长.
知识点三
设交点式确定二次函数的表达式
11.已知抛物线y=ax2+bx+c(a≠0)与x轴,y轴分别相交于A(-1,0),B(3,0),C(0,3)三点,则该抛物线的解析式是__________________.
12.已知抛物线经过点A(5,0)、B(6,-6)和原点,求抛物线的表达式.
13.如图所示,在平面直角坐标系中抛物线y=x2+bx+c与x轴交于点A(3,0),点B(-1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)过点D(0,3)作直线MN∥x轴,点P在直线MN上且S△PAC=S△DBC,求点P的坐标.
巩固提高全练
14.如图①,单孔拱桥的形状近似抛物线形,建立如图②所示的平面直角坐标系,在正常水位时,水面宽度OA为12m,拱桥的最高点B到水面OA的距离为6m,则抛物线的解析式为________________.
15.如图所示,在平面直角坐标系中,抛物线y=ax2+bx-2交x轴于A,B两点,交y轴于点C,且OA=2OC=8OB.点P是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若PC∥AB,求点P的坐标.
16.如图所示,直线y=x+n与抛物线y=ax2+bx+5(a≠0)相交于A(1.2)和B(4,m)两点,点P是线段AB上异于A,B的动点,过点P作PD⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
17.已知抛物线y=ax2+bx+1经过点(1,-2),(-2,13).
(1)求a,b的值;
(2)若(5,y1).(m,y2)是抛物线上不同的两点,且y2=12-y1,求m的值.
18.如图所示,开口向下的抛物线与x轴交于点A(-1.0),B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
19.如图①,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线的绳子.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图②),使左边抛物线F1的最低点距MN
1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为.设MN离AB的距离为m,抛物线F2的顶点离地面的距离为k,当2≤k≤2.5时,求m的取值范围.
20.如图所示,抛物线y=ax2-3ax-4a经过点C(0,2),交x轴于点A、B(点A在点B左侧),连接BC,直线y=kx+1(k>0)与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.
(1)求抛物线的解析式及点A,B的坐标;
(2)是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.
参考答案
1.C
2.
3.解析
设抛物线的表达式为y=ax2+b+c(a≠0),将(-2,6),(2,-4),(3,1)分别代入,得,解得,
所以这条抛物线的表达式为.
4.解析
(1)∵某抛物线与抛物线y=-3x2+2x-5的形状和开口方向均相同,
∴设此抛物线的表达式为y=-3x2+bx+c,∵该抛物线过点A(1,2),B(4,5),
∴,解得,∴此抛物线的表达式y=-3x2+16x-11.
(2).
∴此抛物线的顶点坐标为.
5.解析
∵抛物线y=ax2+2ax+c的对称轴为直线x==-1,抛物线与x轴的交点为A(-3,0)和B,∴点B的坐标为(1,0).
∵∠ACO=∠CBO,∴tan∠ACO=tan∠CBO,即,即,OC=.
将A(-3,0),C(0,3)代入y=ax2+2ax+c,得,解得.
∴抛物线的表达式为.
6.B
7.D
8.
9.
0.2
10.解析
(1)设y=a(x-0.4)2+3.32(a≠0),
把x=0,y=3代入,得3=a(0-0.4)2+3.32.解得a=-2.
∴抛物线的函数表达式为y=-2(x-0.4)2+3.32.
(2)把y=2.6代入y=-2(x-0.4)2+3.32,得2.6=-2(x-0.4)2+3.32.
解得x1=-0.2(舍去),x2=1.∴0D的长为1
m.
y=-x2+2x+3
12.解析
因为抛物线经过点A(5,0)和原,所以设抛物线的表达式为y=ax(x-5)(a≠0)将B(6,6)代人,得-6=6a(6-5),解得a=-1.
所以抛物线的表达式为y=-x2+5x.
13.解析
(1)解法一:抛物线y=x2+bx+c点A(3,0),点B(-1,0),
∴y=(x-3)(x+1)=x2-2x-3.
解法二:将点A(3,0),点B(-1,0)代入y=x2+bx+c,
得,解得.∴y=x2-2x-3.
(2)易知点C的坐标为(0,-3),∴S△DBC=×6×1=3,∴S△PAC=3.
设P(x,3),直线CP与x轴的交点为Q,则S△PAC=×6×AQ,∴AQ=1,
∴点Q的坐标为(2,0)或(4,0),∴直线CQ的表达式为y=x-3或y=x-3,
当y=3时,x=4或x=8,∴点P的坐标为(4,3)或(8,3).
14.
15.解析
(1)把x=0代入y=ax2+bx-2,得y=-2,∴点C的坐标为(0,-2).
∵OA=20C=80B,∴点A的坐标为(-4,0),点B的坐标为.
设抛物线的表达式为y=a(x+4)(x-),
将点C(O,-2)代入,得-2=-2a.解得a=1.
故抛物线的表达式为y=(x+4)(x-)=x2+x-2.
(2)抛物线的对称轴为直线x=-.
当PC∥AB时,点P,C的纵坐标相同,点P的横坐标为-×2=-.
∴点P的坐标为(-,-2).
16.解析
(1)把A(1,2)代入y=x+n,得1+n=2.解得n=1.
∴一次函数的解析式为y=x+1.把B(4,m)代入y=x+1,得m=4+1=5.
∴B的坐标为(4,5).把A(1,2),B(4,5)代入y=ax2+bx+5,
得,解得,∴抛物线的解析式为y=x2-4x+5.
(2)存在设P的坐标为(t,t+1)(1<t<4).
∵PD⊥x轴,∴C的坐标为(t,t2-4t+5).
∴PC=t+1-(t2-4t+5)=-t2+5t-4=.
∴当t=时,PC的长有最大值,最大值为.
17.解析
(1)把点(1,-2),(-2,13)入y=ax2+bx+1,
得,解得.
(2)由(1)得函数解析式为y=x2-4x+1,把(5,y1)代入y=x2-4x+1,得y1=6.
∴y2=12-y1=6.∵y1=y2,抛物线的对称轴为直线x==2.∴m=2×2-5=-1.
18.解析
(1)∵A(-1,0),B(2,0),C(0,4),
∴设抛物线的解析式为y=a(x+1)(x-2),
将C(0,4)代入,得4=-2a.解得a=-2.
∴该抛物线的解析式为y=-2(x+1)(x-2)=-2x2+2x+4.
(2)如图,连接OP,设点P的坐标为(m,-2m2+2m+4)(0<m<2),
∵A(-1,0),B(2,0),C(0,4),∴OA=1,OC=4,0B=2.
∴S四边形CABP=S△OAC+S△OCP+S△OPB
=×1×4+×4m+×2×(-2m2+2m+4)=-2m2+4m+6=-2(m-1)2+8.
∴当m=1时,S的最大值为8.
19.解析
(1)∵a=>0,∴抛物线的顶点为最低点,
∴,∴绳子最低点离地面的距离为米.
(2)由(1)可知,BD=8,令x=0,得y=3,∴A(0,3),C(8,3).
由题意得,抛物线F1的顶点坐标为(2,1.8),设F1的解析式为y=a1(x-2)2+1.8(a1≠0),将(0,3)代入,得4a1+1.8=3解得a1=0.3,
∴抛物线F1的解析式为y=0.3(x-2)2+1.8.
当x=3时,y=0.3×1+1.8=2.1,∴MN的长度为2.1米.
(3)∵MN=CD=3,∴根据抛物线的对称性可知抛物线F2的顶点在线段ND的垂直平分线上,∴抛物线F2的顶点坐标为(m+4,k).∴抛物线F2的解析式为.
把C(8,3)代入,得,∴,∴.
∴k是关于m的二次函数.又∵m<8,∴k随m的增大而增大.
当k=2时,(m-8)2+3=2,解得m1=4,m2=12(不符合题意,舍去).
当k=2.5时,(m-8)2+3=2.5,解得m3=8-2,m4=8+2(不符合题意,舍去).∴m的取值范围是4≤m≤8-2.
20.解析
(1)把C(0,2)代入y=ax2-3ax-4a,得-4a=2解得a=-.
则抛物线的解析式为.
由于=-(x+1)(x-4).
故A的坐标为(-1,0),B的坐标为(4,0).
(2)存在理由如下:
由题意知,点E位于y轴右侧,作EG∥y轴,交BC于点G,如图.
∴CD∥EG.∴△CDF∽△GEF,∴.
∵直线y=kx+1(k>0)与y轴交于点D,∴D(0,1),
∴CD=2-1=1.∴.
设BC所在直线的解析式为y=mx+n(m≠0).
将B(4,0),C(0,2)代入,得,解得.
∴直线BC的解析式是y=-x+2.
设E(t,),则G(t,-t+2),其中0<t<4.
∴EG=()-(-t+2)=-(t-2)2+2.
∴.
∵,∴当t=2时,存在最大值,最大值为2,此时点E的坐标是(2,3).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
