苏教版数学五年级上册 ● 钉子板上的多边形(3) (教案)
文档属性
| 名称 | 苏教版数学五年级上册 ● 钉子板上的多边形(3) (教案) |  | |
| 格式 | docx | ||
| 文件大小 | 33.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 11:39:06 | ||
图片预览


文档简介
钉子板上的多边形
[教学内容]
小学五年级数学(苏教版)上册第108~109页“钉子板上的多边形”规律探索。
[教学目标]
1、使学生在操作、观察、猜测、验证等活动中,发现在钉子板上围出的多边形与它的边所经过的钉子数,以及多边形内部钉子数的关系,会用含有字母的式子表示发现的规律。
(
1cm
)2、使学生在探索规律、发现和表达规律的过程中,培养合作、交流、表达能力,发展观察、比较、推理、归纳和概括等思维能力,体会用字母表示关系的简洁性,积累数学活动经验。
3、使学生获得探索规律成功的体验,树立学习数学的自信心,感受数学规律的奇妙,对数学产生好奇心,提高学习数学的兴趣和积极性。
[教学重点]
探索钉子板上多边形的面积与多边形边上钉子数、内部钉子数之间的关系。
[教学难点]
归纳多边形的面积与多边形边上钉子数、内部钉子数之间的关系,并用含有字母的式子表示发现的规律。
[教学准备]
学生准备点子图练习纸、探究表格。教师准备钉子板、皮筋、多媒体演示课件。
[教学过程]
引入问题,初步感知
1、出示钉子板。
出示钉子板,指出每两个钉子之间为1厘米,围一个梯形,说一说它的面积是多少?你是怎么知道的?
在这些用钉子板围出的图形里还隐藏着很有趣的数学规律,今天这节课就让我们一起来探究钉子板上围出的多边形里隐藏的规律。
(
1cm
1cm
①
②
③
④
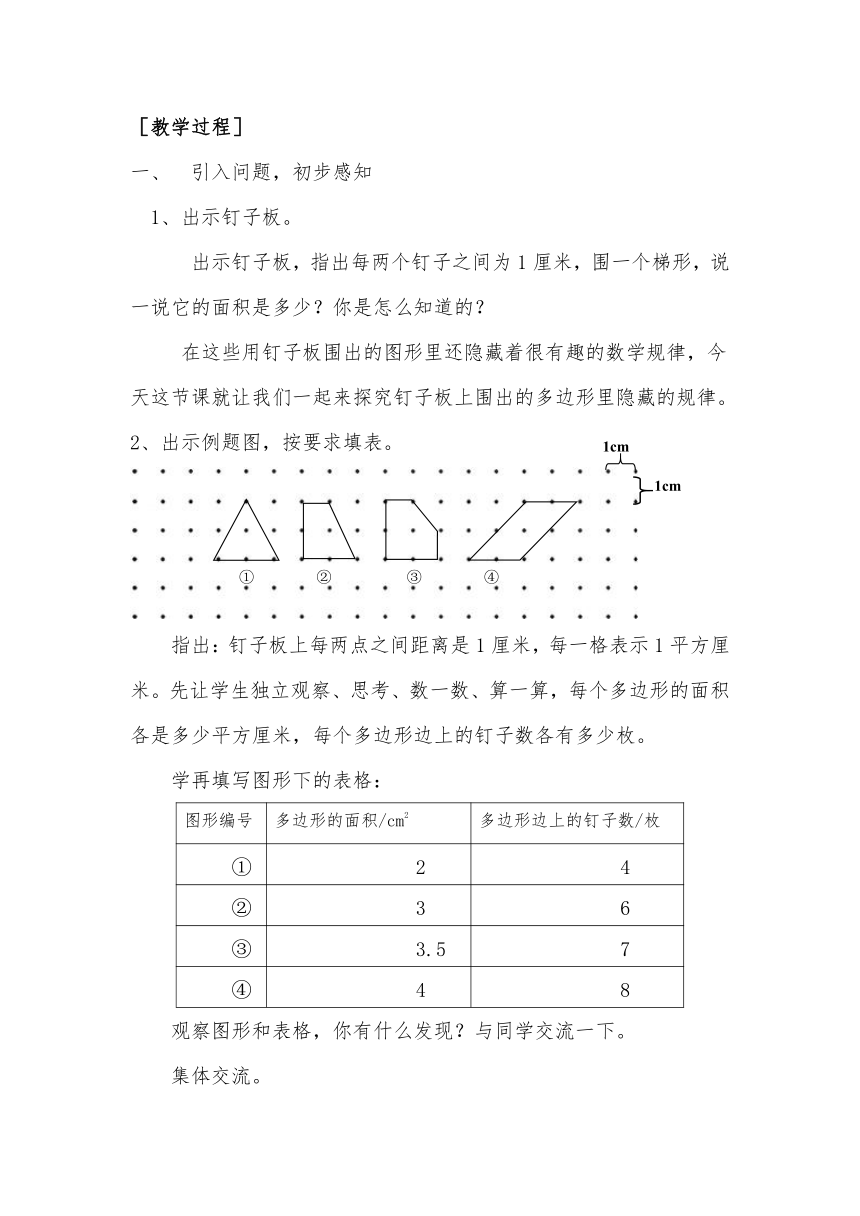
)出示例题图,按要求填表。
指出:钉子板上每两点之间距离是1厘米,每一格表示1平方厘米。先让学生独立观察、思考、数一数、算一算,每个多边形的面积各是多少平方厘米,每个多边形边上的钉子数各有多少枚。
学再填写图形下的表格:
图形编号
多边形的面积/cm2
多边形边上的钉子数/枚
①
1
2
4
②
2
3
6
③
3
3.5
7
④
4
4
8
观察图形和表格,你有什么发现?与同学交流一下。
集体交流。
引导学生得出以下几点:
(1)这些多边形,边上的钉子数越多,面积就越大。
(2)仔细观察,得出这些多边形的面积数是它们边上钉子数的一半
(3)这些图形内都只有1枚钉子。
小结:多边形内只有1枚钉子,它的面积是它边上钉子数的一半。
说明:为了更简洁、方便地表示出这个规律,我们可以用字母来表示。如果用n表示多边形边上钉子数的数值,用S表示多边形面积的数值,那上面发现的这个规律可以怎样表示?
简单交流后指名学生回答。板书:S=n÷2
二、合作交流,深入探究
1、观察比较,反思质疑。
问:是不是钉子板上围成的每一个多边形都符合这个规律呢?请大家观察第2个钉子图,并且利用刚才的式子验证一下多边形的面积格数是不是它们边上钉子数的一半。
提问:同样在这个点子图上围的多边形,为什么第二、第三不符合规律呢?(多边形中间钉子数不是一个)
提问:第一个多边形为什么就符合这个规律呢?(中间只有1枚钉子)
说明:这个规律的成立是有前提条件的。只有当图形内只有1枚钉子时,S=n÷2这个规律才成立。因此,多边形的面积不仅和多边形边上的钉子数有关,还与多边形内部的钉子数有关。
2、探究:多边形内有2枚钉子时,面积与边上钉子数的关系。
观察、思考第三幅钉子板上围出内部有2枚钉子的不同的多边形,再完成下面的表格:
图形编号
多边形内的钉子数/枚(a)
多边形边上的钉子数/枚(n)
多边形的面积/cm2(S)
①
?
?
②
?
?
③
?
?
要求:
(1)每位同学各自数出多边形边上钉子数,算出面积。
(2)把图形相应的数据填到表格里。
(3)小组讨论:如果多边形内有2枚钉子,多边形的面积与它边上钉子数又有什么关系?
全班交流,展示填写的表格。
说说你们的发现:当多边形内有2枚钉子时,围成的多边形的面积是边上的钉子数的一半再加上1。
用含有字母的式子表示多边形的面积:当多边形内有2枚钉子时,S=n÷2+1
在钉子板上围一个内部有2枚钉子的多边形验证:围成的多边形的面积是不是边上的钉子数的一半再加上1。
指名展示所围成的图形,说说面积与边上钉子数的关系。
三、大胆猜想,验证规律
1、请同学们大胆猜想一下。
如果多边形内有3枚、4枚钉子,多边形的面积与它边上钉子数又有怎样的关系呢?
思考,把你的想法与身边的同学说一说。
学生结合上面的规律猜想:多边形内有3枚钉子时,S=n÷2+2;
多边形内有4枚钉子时,S=n÷2+3
。
2、
验证规律:观察第四幅钉子板上围出的不同多边形,再完成下面的表格:
图形编号
多边形内的钉子数/枚?(a)
多边形边上的钉子数/枚?(n)
多边形的面积/平方厘米?(S)
验证的结果(平方厘米?)
①
S?=
②
S?=
③
S?=
④
S?=
3、全班交流。
四、概括规律
如果多边形内有a枚钉子,该怎样用含有字母的式子表示多边形的面积呢?
引导学生观察板书。
多边形内的钉子数
多边形边上的钉子数
多边形的面积
1
n
S=n÷2
2
n
S=n÷2+1
3
n
S=n÷2+2
4
n
S=n÷2+3
…
…
…
a
n
S=
学生归纳,得出规律。板书:S=n÷2+a―1
验证:在钉子板上任意围一个多边形,数一数、算一算是不是符合我们发现的规律。
指名展示,,说说所围成的图形面积与边上钉子数的关系。
思考:当a=0的时候,也符合这样的规律吗?我们围一个图形来看一看,发现:当a=0时,可以看作S=n÷2+0—1,算出的数与实际面积一样,符合规律。
全课小结
今天我们一起研究了钉子板上多边形面积与钉子数之间的关系。
你有那些收获或体会?还有哪些疑问?
[教学内容]
小学五年级数学(苏教版)上册第108~109页“钉子板上的多边形”规律探索。
[教学目标]
1、使学生在操作、观察、猜测、验证等活动中,发现在钉子板上围出的多边形与它的边所经过的钉子数,以及多边形内部钉子数的关系,会用含有字母的式子表示发现的规律。
(
1cm
)2、使学生在探索规律、发现和表达规律的过程中,培养合作、交流、表达能力,发展观察、比较、推理、归纳和概括等思维能力,体会用字母表示关系的简洁性,积累数学活动经验。
3、使学生获得探索规律成功的体验,树立学习数学的自信心,感受数学规律的奇妙,对数学产生好奇心,提高学习数学的兴趣和积极性。
[教学重点]
探索钉子板上多边形的面积与多边形边上钉子数、内部钉子数之间的关系。
[教学难点]
归纳多边形的面积与多边形边上钉子数、内部钉子数之间的关系,并用含有字母的式子表示发现的规律。
[教学准备]
学生准备点子图练习纸、探究表格。教师准备钉子板、皮筋、多媒体演示课件。
[教学过程]
引入问题,初步感知
1、出示钉子板。
出示钉子板,指出每两个钉子之间为1厘米,围一个梯形,说一说它的面积是多少?你是怎么知道的?
在这些用钉子板围出的图形里还隐藏着很有趣的数学规律,今天这节课就让我们一起来探究钉子板上围出的多边形里隐藏的规律。
(
1cm
1cm
①
②
③
④
)出示例题图,按要求填表。
指出:钉子板上每两点之间距离是1厘米,每一格表示1平方厘米。先让学生独立观察、思考、数一数、算一算,每个多边形的面积各是多少平方厘米,每个多边形边上的钉子数各有多少枚。
学再填写图形下的表格:
图形编号
多边形的面积/cm2
多边形边上的钉子数/枚
①
1
2
4
②
2
3
6
③
3
3.5
7
④
4
4
8
观察图形和表格,你有什么发现?与同学交流一下。
集体交流。
引导学生得出以下几点:
(1)这些多边形,边上的钉子数越多,面积就越大。
(2)仔细观察,得出这些多边形的面积数是它们边上钉子数的一半
(3)这些图形内都只有1枚钉子。
小结:多边形内只有1枚钉子,它的面积是它边上钉子数的一半。
说明:为了更简洁、方便地表示出这个规律,我们可以用字母来表示。如果用n表示多边形边上钉子数的数值,用S表示多边形面积的数值,那上面发现的这个规律可以怎样表示?
简单交流后指名学生回答。板书:S=n÷2
二、合作交流,深入探究
1、观察比较,反思质疑。
问:是不是钉子板上围成的每一个多边形都符合这个规律呢?请大家观察第2个钉子图,并且利用刚才的式子验证一下多边形的面积格数是不是它们边上钉子数的一半。
提问:同样在这个点子图上围的多边形,为什么第二、第三不符合规律呢?(多边形中间钉子数不是一个)
提问:第一个多边形为什么就符合这个规律呢?(中间只有1枚钉子)
说明:这个规律的成立是有前提条件的。只有当图形内只有1枚钉子时,S=n÷2这个规律才成立。因此,多边形的面积不仅和多边形边上的钉子数有关,还与多边形内部的钉子数有关。
2、探究:多边形内有2枚钉子时,面积与边上钉子数的关系。
观察、思考第三幅钉子板上围出内部有2枚钉子的不同的多边形,再完成下面的表格:
图形编号
多边形内的钉子数/枚(a)
多边形边上的钉子数/枚(n)
多边形的面积/cm2(S)
①
?
?
②
?
?
③
?
?
要求:
(1)每位同学各自数出多边形边上钉子数,算出面积。
(2)把图形相应的数据填到表格里。
(3)小组讨论:如果多边形内有2枚钉子,多边形的面积与它边上钉子数又有什么关系?
全班交流,展示填写的表格。
说说你们的发现:当多边形内有2枚钉子时,围成的多边形的面积是边上的钉子数的一半再加上1。
用含有字母的式子表示多边形的面积:当多边形内有2枚钉子时,S=n÷2+1
在钉子板上围一个内部有2枚钉子的多边形验证:围成的多边形的面积是不是边上的钉子数的一半再加上1。
指名展示所围成的图形,说说面积与边上钉子数的关系。
三、大胆猜想,验证规律
1、请同学们大胆猜想一下。
如果多边形内有3枚、4枚钉子,多边形的面积与它边上钉子数又有怎样的关系呢?
思考,把你的想法与身边的同学说一说。
学生结合上面的规律猜想:多边形内有3枚钉子时,S=n÷2+2;
多边形内有4枚钉子时,S=n÷2+3
。
2、
验证规律:观察第四幅钉子板上围出的不同多边形,再完成下面的表格:
图形编号
多边形内的钉子数/枚?(a)
多边形边上的钉子数/枚?(n)
多边形的面积/平方厘米?(S)
验证的结果(平方厘米?)
①
S?=
②
S?=
③
S?=
④
S?=
3、全班交流。
四、概括规律
如果多边形内有a枚钉子,该怎样用含有字母的式子表示多边形的面积呢?
引导学生观察板书。
多边形内的钉子数
多边形边上的钉子数
多边形的面积
1
n
S=n÷2
2
n
S=n÷2+1
3
n
S=n÷2+2
4
n
S=n÷2+3
…
…
…
a
n
S=
学生归纳,得出规律。板书:S=n÷2+a―1
验证:在钉子板上任意围一个多边形,数一数、算一算是不是符合我们发现的规律。
指名展示,,说说所围成的图形面积与边上钉子数的关系。
思考:当a=0的时候,也符合这样的规律吗?我们围一个图形来看一看,发现:当a=0时,可以看作S=n÷2+0—1,算出的数与实际面积一样,符合规律。
全课小结
今天我们一起研究了钉子板上多边形面积与钉子数之间的关系。
你有那些收获或体会?还有哪些疑问?
