冀教版九上数学 23.2.1 中位数和众数的认识 课件(共32张PPT)
文档属性
| 名称 | 冀教版九上数学 23.2.1 中位数和众数的认识 课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 08:34:28 | ||
图片预览









文档简介
(共32张PPT)
23.2
中位数和众数
第1课时
中位数和众数
的认识
第23章
数据分析
课时导入
复习提问
引出问题
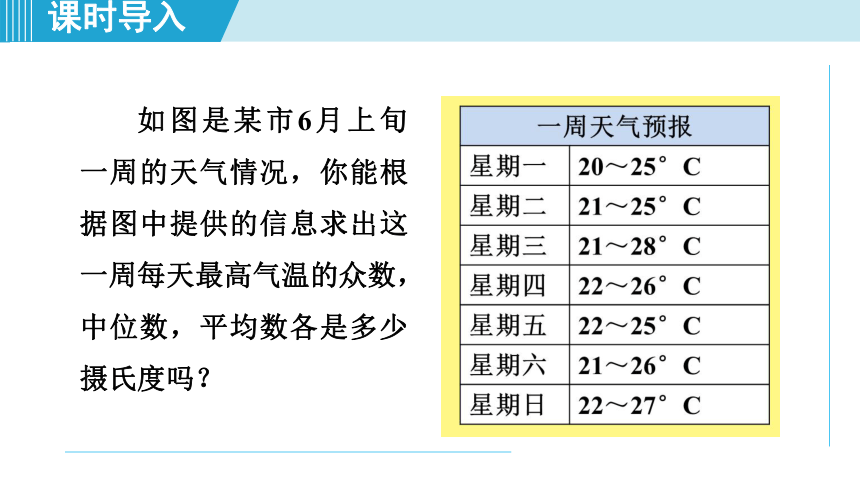
如图是某市6月上旬一周的天气情况,你能根据图中提供的信息求出这一周每天最高气温的众数,中位数,平均数各是多少摄氏度吗?
知识点
中位数
知1-讲
感悟新知
1
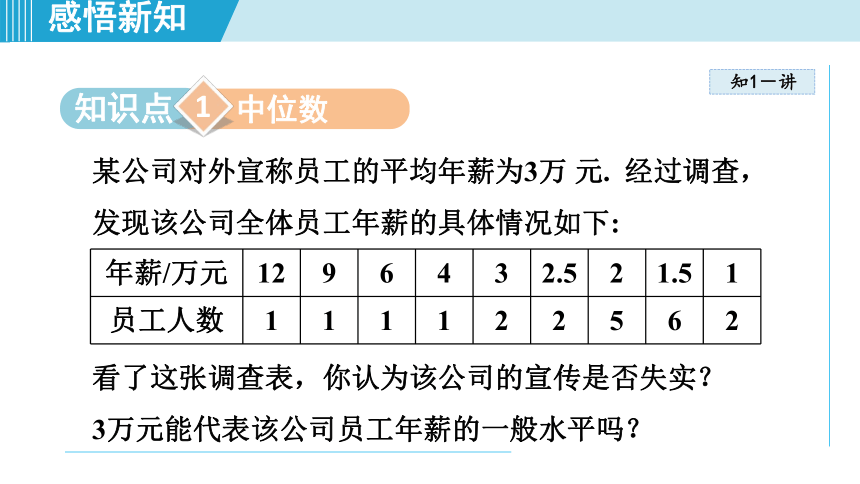
某公司对外宣称员工的平均年薪为3万
元.
经过调查,发现该公司全体员工年薪的具体情况如下:
看了这张调查表,你认为该公司的宣传是否失实?
3万元能代表该公司员工年薪的一般水平吗?
年薪/万元
12
9
6
4
3
2.5
2
1.5
1
员工人数
1
1
1
1
2
2
5
6
2
知1-讲
感悟新知
在公司的21名员工中,年薪不低于3万元的只有6人
而低于3万元的却有15人,并且其中有13人不
超过2万元,8人不超过1.5万元,年薪1.5万元的人
数最多,为6人。
如果我们将上面的21个数据按大小顺序排列,
不难发现数据2万元处于中间位置,也就是说:
(1)年薪不低于2万元的人数不少于一半(13人);
(2)年薪不高于2万元的人数也不少于一半(13人).
知1-讲
归
纳
感悟新知
一般地,将n个数据按大小顺序排列,
如果n为奇数,
那么把处于中间位置的数据叫做这组数据的中位数
(median);如果n为偶数,那么把处于中间位置的两个
数据的平均数叫做这组数据的中位数.
如图,
图(1)中5个数据的中位数
为x3,图(2)中6个数据的中位数为
知1-讲
感悟新知
1.一组数据的中位数是唯一的,它可能是这组数据中的
一个数,也可能不是,如9,8,8,8,7,6,5,4的
中位数是
2.中位数与数据的排列位置有关,当一组数据中的个别数据
较大时,可用中位数来描述这组数据的集中趋势.
知1-讲
感悟新知
3.求中位数的步骤:
(1)将数据由小到大(或由大到小)排列;
(2)数清数据个数是奇数还是偶数,如果数据个数为奇数,则
取中间的数作为中位数;如果数据个数为偶数,则取中间
两数的平均数作为中位数.
知1-讲
感悟新知
特别提醒:
1.
一组数据的中位数是唯一的,它可能是这组数据中的某个数,也可能不是这组数据中的数.
2.中位数是一组数据的“中等水平”的一个代表,反映了一组数据的集中趋势.
3.用中位数作为一组数据的代表,可靠性比较差,因为它不能充分利用所有的数据信息,但它不受极端值的影响,当一组数据中有个别数据变动较大时,可用中位数来描述这组数据的集中趋势.
感悟新知
知1-练
例
1
(中考·自贡)某班七个合作学习小组人数如下:
4,5,5,x,6,7,8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.5 B.5.5 C.6 D.7
导引:
根据平均数的定义得,4+5+5+x+6+7+8=6×7,
解得x=7.
从小到大排列这组数据为4,5,5,6,7,7,8,
所以中位数是6.
C
知1-讲
总
结
感悟新知
求一组数据的中位数的方法:先将数据按照从小
到大(或从大到小)的顺序进行排列,然后根据数据的
个数确定中位数,如果数据的个数是奇数,则处于中
间位置的数为这组数据的中位数;如果数据的个数是
偶数,则中间两个数据的平均数为这组数据的中位数,
注意,中位数不一定是这组数据中的数.
感悟新知
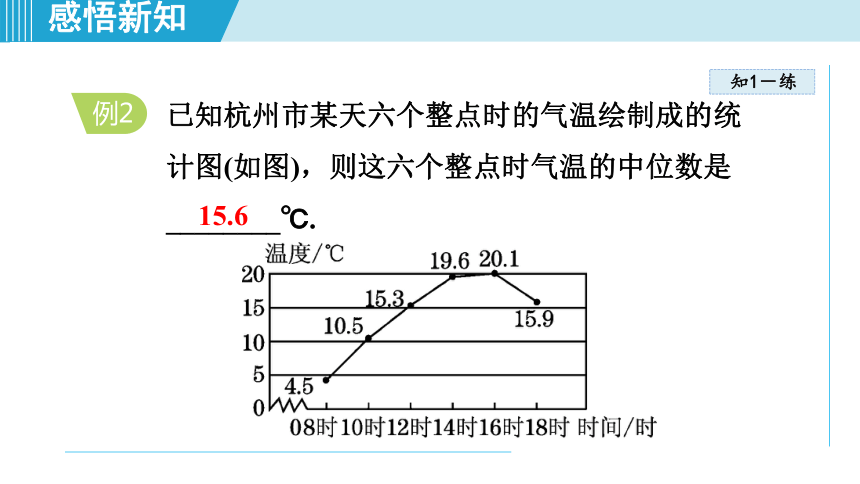
例2
已知杭州市某天六个整点时的气温绘制成的统计图(如图),则这六个整点时气温的中位数是________℃.
15.6
知1-练
感悟新知
知1-练
导引:
根据中位数的定义解答.将这组数据按从小到大重
新排列,求出最中间两个数的平均数即可.
把这些数据从小到大排列为:
4.5,10.5,15.3,15.9,19.6,20.1,
最中间的两个数的平均数是:
(15.3+15.9)÷2=15.6(℃),
则这六个整点时气温的中位数是15.6
℃.
知1-讲
总
结
感悟新知
掌握中位数的定义是解答本题的关键,中位数是
将一组数据从小到大(或从大到小)重新排列后,最中
间的那个数或最中间两个数的平均数.
感悟新知
1 (中考·河南)在一次体育测试中,小芳所在小组8人的成绩分别是:46,47,48,48,49,49,49,50,则8人体育成绩的中位数是( )
A.47
B.48
C.48.5
D.49
知1-练
感悟新知
2 (中考·泰安)某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个):35,38,42,44,47,45,45,则这组数据的中位数、平均数分别是( )
A.42,
42
B.43,42
C.43,
43
D.44,
43
知1-练
感悟新知
(中考·德州)已知一组数据:6,2,8,x,7,它们的平均数是6,则这组数据的中位数是
( )
A.
7
B.6
C.5
D.4
知1-练
知识点
众
数
知2-讲
感悟新知
2
观察与思考
某班用无记名投票的方式选班长,5名候选人分别编为1号,2号,3号,4号,5号,投票结果如下表:
在这个问题中,我们最关注的是什么?
候选人
1号
2号
3号
4号
5号
合计
计票
正
正正正
正正
正
正一
50
票数
7
18
10
9
6
50
感悟新知
知2-讲
参加投票的50人,每人选择一名候选人的号
码,把这50个号码看成一组数据,由于2号出现
的次数最多,按规则,2号候选人应当选为班长.
知2-讲
归
纳
感悟新知
一般地,把一组数据中出现次数最多的那个数据
叫做众数(mode).一组数据的众数可能不止一个,也可能没有众数.
感悟新知
知2-讲
1.定义:一般地,把一组数据中出现次数最多的
那个数据叫做众数.
2.要点精析
(1)一组数据的众数一定出现在这组数据中;
(2)一组数据的众数可能不止一个;
(3)一组数据也可能没有众数,因为有可能数据出现的
次数相同;
(4)众数可以在某种意义上代表这组数据的整体情况.
感悟新知
知2-练
例
3
下面为某班某次数学测试成绩的分布表.已知全班共有38人,且这次数学测试成绩的众数为50分,中位数为60分,则x2-2y的值为( )
A.33 B.50 C.69 D.60
B
成绩/分
20
30
40
50
60
70
90
100
人数
2
3
5
x
6
y
3
4
感悟新知
知2-练
全班共有38人,即2+3+5+x+6+y+3+4=38,
所以x+y=15.
又因为众数为50分,所以x>y,
即x>15-x,解得x>
又因为x为整数,所以x≥8. ①
因为中位数为60分,所以2+3+5+x<6+y+3+4.
整理,得x<y+3.
即x<15-x+3,解得x<9. ②
综合①②,得x=8.
所以y=7.
所以x2-2y=64-14=50.
导引:
知2-讲
总
结
感悟新知
解本题应抓住两点:
(1)众数为50分,说明x>6,x>y;
(2)中位数为60分,说明60分以上(包括60分)的人
数大于60分以下的人数.
感悟新知
例4
统计全班45名学生每天上学路上所用的时间.
如果时间取最接近5的倍数的整数,那么整理后的数据如下表:
求所用时间的平均数、中位数和众数.
所用时间/min
5
10
15
20
25
30
合计
人数/名
2
6
14
12
8
3
45
知2-练
感悟新知
知2-练
45个数据的平均数为
=18(min).
将这45个数据由小到大排序,第23个数据是20
min,
所以中位数是20
min.
所用时间出现最多的是15
min,所以众数是15
min.
解:
知2-讲
总
结
感悟新知
求一组数据的众数的方法:找一组数据的众数,
可用观察法;当不易观察时,可用列表的形式把各
数据出现的次数全部统计出来,即可得出众数.
感悟新知
1 某中学由6名师生组成一个排球队,他们的年龄(单位:岁)如下:
15 16 17 17 17 40
(1)这组数据的平均数为______,中位数为______,众
数为______.
(2)用哪个值作为他们年龄的代表值较好?
2 (1)数据
3,5,3,5,3,6,5,7中,众数是
______和______.
(2)数据3,4,6,5,7,8,9,2中,存在众数吗?为
什么?
知2-练
感悟新知
3
某校九年级(1)班全体学生2016年初中毕业体育
考试的成绩统计如下表:
根据上表中的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是45分
C.该班学生这次考试成绩的中位数是45分
D.该班学生这次考试成绩的平均数是45分
成绩/分
35
39
42
44
45
48
50
人数/人
2
5
6
6
8
7
6
知2-练
感悟新知
4
某电脑公司销售部为了制订下个月的销售计划,
对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )
A.19台,20台,14台
B.19台,20台,20台
C.18.4台,20台,20台
D.18.4台,25台,20台
知2-练
课堂小结
中位数:
1.在计算一组数据的中位数时,其步骤为:
(1)将这组数据按从小到大(或从大到小)的顺序排列;
(2)找到处在最中间位置的一个数或最中间的两个数的
平均数即为中位数.
2.求中位数时,先将数据由小到大或由大到小排列,若
这组数据是奇数个,则最中间的数据是中位数;若
这组数据是偶数个,则最中间的两个数据的平均数
是中位数。
课堂小结
众数:
1.若几个数据出现的次数相同,并且比其他数据出现的
次数都多,那么这几个数据都是这组数据的众数;当
所有的数出现的次数一样多时,无众数.
2.众数是一组数据中的某个或几个数据,其单位与数据
的单位相同.
3.众数是一组数据中出现次数最多的数,而不是该数据
出现的次数.
必做:
请完成教材课后习题
课后作业
作业
23.2
中位数和众数
第1课时
中位数和众数
的认识
第23章
数据分析
课时导入
复习提问
引出问题
如图是某市6月上旬一周的天气情况,你能根据图中提供的信息求出这一周每天最高气温的众数,中位数,平均数各是多少摄氏度吗?
知识点
中位数
知1-讲
感悟新知
1
某公司对外宣称员工的平均年薪为3万
元.
经过调查,发现该公司全体员工年薪的具体情况如下:
看了这张调查表,你认为该公司的宣传是否失实?
3万元能代表该公司员工年薪的一般水平吗?
年薪/万元
12
9
6
4
3
2.5
2
1.5
1
员工人数
1
1
1
1
2
2
5
6
2
知1-讲
感悟新知
在公司的21名员工中,年薪不低于3万元的只有6人
而低于3万元的却有15人,并且其中有13人不
超过2万元,8人不超过1.5万元,年薪1.5万元的人
数最多,为6人。
如果我们将上面的21个数据按大小顺序排列,
不难发现数据2万元处于中间位置,也就是说:
(1)年薪不低于2万元的人数不少于一半(13人);
(2)年薪不高于2万元的人数也不少于一半(13人).
知1-讲
归
纳
感悟新知
一般地,将n个数据按大小顺序排列,
如果n为奇数,
那么把处于中间位置的数据叫做这组数据的中位数
(median);如果n为偶数,那么把处于中间位置的两个
数据的平均数叫做这组数据的中位数.
如图,
图(1)中5个数据的中位数
为x3,图(2)中6个数据的中位数为
知1-讲
感悟新知
1.一组数据的中位数是唯一的,它可能是这组数据中的
一个数,也可能不是,如9,8,8,8,7,6,5,4的
中位数是
2.中位数与数据的排列位置有关,当一组数据中的个别数据
较大时,可用中位数来描述这组数据的集中趋势.
知1-讲
感悟新知
3.求中位数的步骤:
(1)将数据由小到大(或由大到小)排列;
(2)数清数据个数是奇数还是偶数,如果数据个数为奇数,则
取中间的数作为中位数;如果数据个数为偶数,则取中间
两数的平均数作为中位数.
知1-讲
感悟新知
特别提醒:
1.
一组数据的中位数是唯一的,它可能是这组数据中的某个数,也可能不是这组数据中的数.
2.中位数是一组数据的“中等水平”的一个代表,反映了一组数据的集中趋势.
3.用中位数作为一组数据的代表,可靠性比较差,因为它不能充分利用所有的数据信息,但它不受极端值的影响,当一组数据中有个别数据变动较大时,可用中位数来描述这组数据的集中趋势.
感悟新知
知1-练
例
1
(中考·自贡)某班七个合作学习小组人数如下:
4,5,5,x,6,7,8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.5 B.5.5 C.6 D.7
导引:
根据平均数的定义得,4+5+5+x+6+7+8=6×7,
解得x=7.
从小到大排列这组数据为4,5,5,6,7,7,8,
所以中位数是6.
C
知1-讲
总
结
感悟新知
求一组数据的中位数的方法:先将数据按照从小
到大(或从大到小)的顺序进行排列,然后根据数据的
个数确定中位数,如果数据的个数是奇数,则处于中
间位置的数为这组数据的中位数;如果数据的个数是
偶数,则中间两个数据的平均数为这组数据的中位数,
注意,中位数不一定是这组数据中的数.
感悟新知
例2
已知杭州市某天六个整点时的气温绘制成的统计图(如图),则这六个整点时气温的中位数是________℃.
15.6
知1-练
感悟新知
知1-练
导引:
根据中位数的定义解答.将这组数据按从小到大重
新排列,求出最中间两个数的平均数即可.
把这些数据从小到大排列为:
4.5,10.5,15.3,15.9,19.6,20.1,
最中间的两个数的平均数是:
(15.3+15.9)÷2=15.6(℃),
则这六个整点时气温的中位数是15.6
℃.
知1-讲
总
结
感悟新知
掌握中位数的定义是解答本题的关键,中位数是
将一组数据从小到大(或从大到小)重新排列后,最中
间的那个数或最中间两个数的平均数.
感悟新知
1 (中考·河南)在一次体育测试中,小芳所在小组8人的成绩分别是:46,47,48,48,49,49,49,50,则8人体育成绩的中位数是( )
A.47
B.48
C.48.5
D.49
知1-练
感悟新知
2 (中考·泰安)某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个):35,38,42,44,47,45,45,则这组数据的中位数、平均数分别是( )
A.42,
42
B.43,42
C.43,
43
D.44,
43
知1-练
感悟新知
(中考·德州)已知一组数据:6,2,8,x,7,它们的平均数是6,则这组数据的中位数是
( )
A.
7
B.6
C.5
D.4
知1-练
知识点
众
数
知2-讲
感悟新知
2
观察与思考
某班用无记名投票的方式选班长,5名候选人分别编为1号,2号,3号,4号,5号,投票结果如下表:
在这个问题中,我们最关注的是什么?
候选人
1号
2号
3号
4号
5号
合计
计票
正
正正正
正正
正
正一
50
票数
7
18
10
9
6
50
感悟新知
知2-讲
参加投票的50人,每人选择一名候选人的号
码,把这50个号码看成一组数据,由于2号出现
的次数最多,按规则,2号候选人应当选为班长.
知2-讲
归
纳
感悟新知
一般地,把一组数据中出现次数最多的那个数据
叫做众数(mode).一组数据的众数可能不止一个,也可能没有众数.
感悟新知
知2-讲
1.定义:一般地,把一组数据中出现次数最多的
那个数据叫做众数.
2.要点精析
(1)一组数据的众数一定出现在这组数据中;
(2)一组数据的众数可能不止一个;
(3)一组数据也可能没有众数,因为有可能数据出现的
次数相同;
(4)众数可以在某种意义上代表这组数据的整体情况.
感悟新知
知2-练
例
3
下面为某班某次数学测试成绩的分布表.已知全班共有38人,且这次数学测试成绩的众数为50分,中位数为60分,则x2-2y的值为( )
A.33 B.50 C.69 D.60
B
成绩/分
20
30
40
50
60
70
90
100
人数
2
3
5
x
6
y
3
4
感悟新知
知2-练
全班共有38人,即2+3+5+x+6+y+3+4=38,
所以x+y=15.
又因为众数为50分,所以x>y,
即x>15-x,解得x>
又因为x为整数,所以x≥8. ①
因为中位数为60分,所以2+3+5+x<6+y+3+4.
整理,得x<y+3.
即x<15-x+3,解得x<9. ②
综合①②,得x=8.
所以y=7.
所以x2-2y=64-14=50.
导引:
知2-讲
总
结
感悟新知
解本题应抓住两点:
(1)众数为50分,说明x>6,x>y;
(2)中位数为60分,说明60分以上(包括60分)的人
数大于60分以下的人数.
感悟新知
例4
统计全班45名学生每天上学路上所用的时间.
如果时间取最接近5的倍数的整数,那么整理后的数据如下表:
求所用时间的平均数、中位数和众数.
所用时间/min
5
10
15
20
25
30
合计
人数/名
2
6
14
12
8
3
45
知2-练
感悟新知
知2-练
45个数据的平均数为
=18(min).
将这45个数据由小到大排序,第23个数据是20
min,
所以中位数是20
min.
所用时间出现最多的是15
min,所以众数是15
min.
解:
知2-讲
总
结
感悟新知
求一组数据的众数的方法:找一组数据的众数,
可用观察法;当不易观察时,可用列表的形式把各
数据出现的次数全部统计出来,即可得出众数.
感悟新知
1 某中学由6名师生组成一个排球队,他们的年龄(单位:岁)如下:
15 16 17 17 17 40
(1)这组数据的平均数为______,中位数为______,众
数为______.
(2)用哪个值作为他们年龄的代表值较好?
2 (1)数据
3,5,3,5,3,6,5,7中,众数是
______和______.
(2)数据3,4,6,5,7,8,9,2中,存在众数吗?为
什么?
知2-练
感悟新知
3
某校九年级(1)班全体学生2016年初中毕业体育
考试的成绩统计如下表:
根据上表中的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是45分
C.该班学生这次考试成绩的中位数是45分
D.该班学生这次考试成绩的平均数是45分
成绩/分
35
39
42
44
45
48
50
人数/人
2
5
6
6
8
7
6
知2-练
感悟新知
4
某电脑公司销售部为了制订下个月的销售计划,
对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )
A.19台,20台,14台
B.19台,20台,20台
C.18.4台,20台,20台
D.18.4台,25台,20台
知2-练
课堂小结
中位数:
1.在计算一组数据的中位数时,其步骤为:
(1)将这组数据按从小到大(或从大到小)的顺序排列;
(2)找到处在最中间位置的一个数或最中间的两个数的
平均数即为中位数.
2.求中位数时,先将数据由小到大或由大到小排列,若
这组数据是奇数个,则最中间的数据是中位数;若
这组数据是偶数个,则最中间的两个数据的平均数
是中位数。
课堂小结
众数:
1.若几个数据出现的次数相同,并且比其他数据出现的
次数都多,那么这几个数据都是这组数据的众数;当
所有的数出现的次数一样多时,无众数.
2.众数是一组数据中的某个或几个数据,其单位与数据
的单位相同.
3.众数是一组数据中出现次数最多的数,而不是该数据
出现的次数.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
