2021-2022学年数学人教版九年级上册22.3 实际问题与二次函数 提升练(Word版含答案)
文档属性
| 名称 | 2021-2022学年数学人教版九年级上册22.3 实际问题与二次函数 提升练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 426.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 18:01:39 | ||
图片预览




文档简介
2021-2022学年数学人教版九年级上册二次函数
——基础提升练(6)实际问题与二次函数
提升练
1.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,则能获取的最大利润是(
)
A.600元
B.625元
C.650元
D.675元
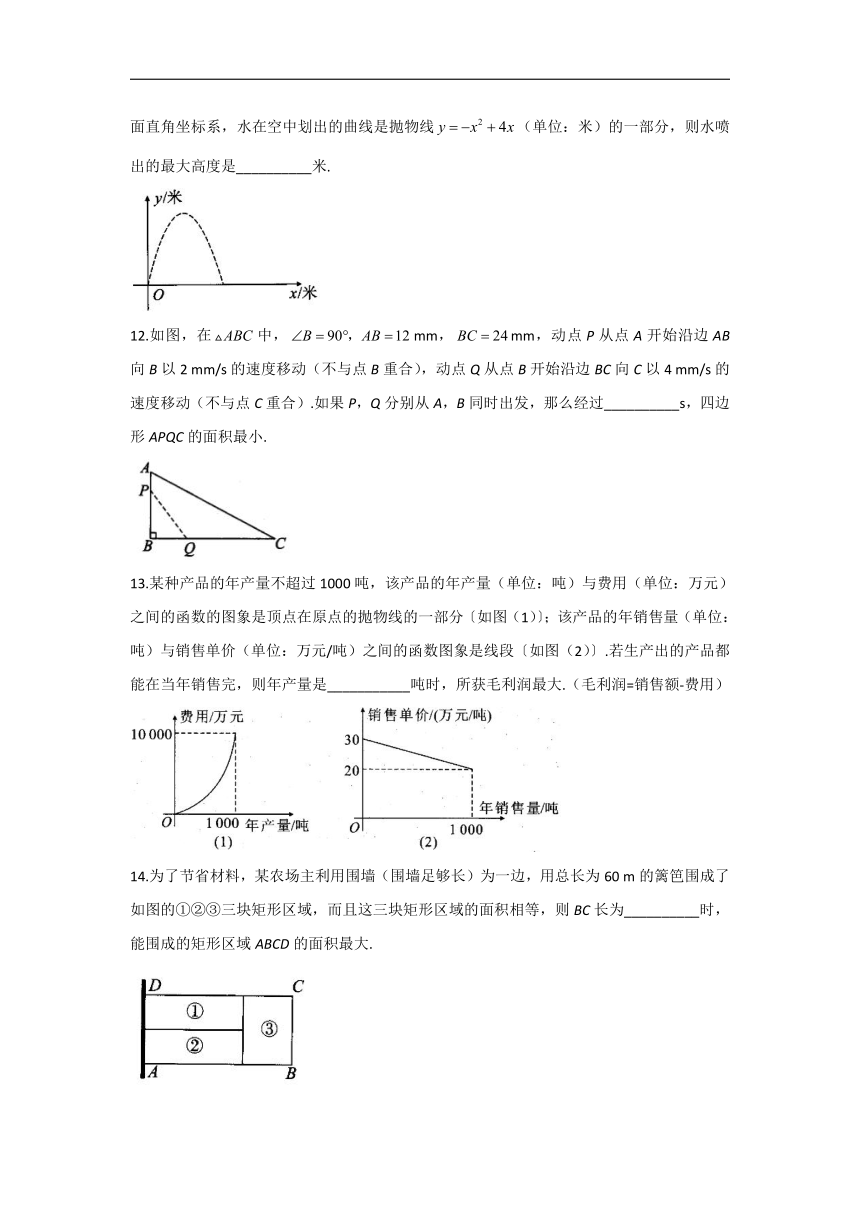
2.一家电脑公司推出一款新型电脑.投放市场以来前3个月的利润情况如图所示,该图可以近似看作抛物线的一部分.则该公司在经营此款电脑过程中,利润最大的月份是(
)
A.第5个月
B.第6个月
C.第7个月
D.第8个月
3.如图,点是线段上的一动点,,分别以和为一边作正方形,用表示这两个正方形的面积之和,下列判断正确的是(
)
A.当是的中点时,最小
B.当是的中点时,最大
C.当是的三等分点时,最小
D.当是的三等分点时,最大
4.如图是抛物线形拱桥,当拱顶高离水面2
m时,水面宽4
m,水面下降2.5
m,水面宽度增加(
)
A.1
m
B.2
m
C.3
m
D.6
m
5.某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天的销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图,则每天的最大利润是(
)
A.180元
B.220元
C.190元
D.200元
6.某宾馆共有80间客房,宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足.若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间的定价确定为(
)
A.252元/间
B.256元/间
C.258元/间
D.260元/间
7.一位篮球运动员在距离篮圈中心水平距离4
m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5
m时,达到最大高度3.5
m,然后准确落入篮筐内.已知篮圈中心距离地面的高度为3.05
m,在如图的平面直角坐标系中,下列说法正确的是(
)
A.此抛物线对应的函数表达式是
B.篮圈中心的坐标是
C.此抛物线的顶点坐标是
D.篮球出手时离地面的高度是2
m
8.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.则该企业每天可以获得的最大销售利润是(
)
A.5500元
B.5000元
C.4800元
D.4500元
9.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃.臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”与加工煎炸时间(单位:分钟)近似满足的函数关系为:(,是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为(
)
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
10.如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图像,其中曲线段AB是以B为顶点的抛物线的一部分.下列说法不正确的是(
)
A.25
min~50
min,王阿姨步行的路程为800
m
B.线段CD对应的函数表达式为
C.5
min~20
min,王阿姨步行速度由慢到快
D.曲线段AB对应的函数表达式为
11.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是__________米.
12.如图,在中,mm,mm,动点P从点A开始沿边AB向B以2
mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4
mm/s的速度移动(不与点C重合).如果P,Q分别从A,B同时出发,那么经过__________s,四边形APQC的面积最小.
13.某种产品的年产量不超过1000吨,该产品的年产量(单位:吨)与费用(单位:万元)之间的函数的图象是顶点在原点的抛物线的一部分〔如图(1)〕;该产品的年销售量(单位:吨)与销售单价(单位:万元/吨)之间的函数图象是线段〔如图(2)〕.若生产出的产品都能在当年销售完,则年产量是___________吨时,所获毛利润最大.(毛利润=销售额-费用)
14.为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为60
m的篱笆围成了如图的①②③三块矩形区域,而且这三块矩形区域的面积相等,则BC长为__________时,能围成的矩形区域ABCD的面积最大.
15.如图,是边长为3cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1
cm/s.当点P到达点B时,P,Q两点停止运动.设点P的运动时间为t(s),解答下列问题:
(1)当t为何值时,是直角三角形?
(2)设四边形APQC的面积为y(),求y()与t(s)的函数关系式.是否存在某一时刻t(s),使得四边形APQC的面积有最值?若存在,求出最值.
答案以及解析
1.答案:B
解析:设降价x元时获取利润y元,则有.,当时,.
2.答案:C
解析:图象过原点,故可设二次函数表达式为.由图可知,图象过点,代入解得,.即该公司在经营此款电脑过程中,利润最大的月份是第7个月.故选C.
3.答案:A
解析:设,则,根据题意,得,所以当时,取得最小值,此时,是的中点.故选A.
4.答案:B
解析:如答图,建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB的中点O且通过点C,则通过画图可知O为原点,抛物线以y轴为对称轴.根据题意,知抛物线顶点C的坐标为,设抛物线对应的函数表达式为,把点A的坐标代入,得,得,抛物线对应的函数表达式为,当时,
,解得,水面下降2.5m,水面宽度增加2
m.故选B.
5.答案:D
解析:设,由图像可知,解得.设销售利润为p元,根据题意,得.p有最大值.当时,.即当销售单价为20元/千克时,每天可获得最大利润是200元.故选D.
6.答案:B
解析:设每天的利润为W元,根据题意,得.当时,不是整数,舍去,当或时,函数取得最大值.又想让客人得到实惠,宾馆应将房间定价确定为256元/间时,才能获得最大利润.故选B.
7.答案:A
解析:抛物线的顶点坐标为可设抛物线对应的函数表达式为篮圈中心在抛物线上,将它的坐标代入上式,得,,选项A正确;由题图可知,篮圈中心的坐标是,选项B错误;由题图可知,此抛物线的顶点坐标是选项C错误;设这次跳投时,球出手处离地面h
m.,当时,这次跳投时,球出手处离地面2.25
m,选项D错误.故选A.
8.答案:D
解析:设销售单价为x元,利润为y元,由题意可得,抛物线开口向下.,对称轴是直线,当时,y有最大值为4500,即销售单价为80元时,每天的销售利润最大,最大利润是4500元.故选D.
9.答案:C
解析:本题考查二次函数的应用.将图象中的三个点代入函数关系中得,,解得,所以函数关系式为.由题意可知,加工煎炸臭豆腐的最佳时间应为抛物线顶点的横坐标,则当分钟时,为最佳时间,故选C.
10.答案:C
解析:25
min~50
min,王阿姨步行的路程为(m),A不符合题意;设线段CD对应的函数表达式为,把点的坐标分别代入,得解得线段CD对应的函数表达式为,B不符合题意;在点A的速度为,在点B的速度为,5
min~20
min,王阿姨步行速度由快到慢,C符合题意;当时,由图像可得m,将代入得,D不符合题意.故选C.
11.答案:4
解析:水在空中划出的曲线是抛物线的一部分,喷水的最大高度就是水在空中划出的抛物线的顶点坐标的纵坐标.顶点坐标为喷水的最大高度为4米.
12.答案:3
解析:设P,Q同时出发后经过的时间为t
s,四边形APQC的面积为S,则有.因为,所以当s时,S取得最小值.
13.答案:750
解析:设年产量为x吨,费用为y万元,销售单价为z万元/吨,则由题图(1)得y与x的函数表达式为.由题图(2)得z与x的函数表达式为.设毛利润为S(万元),则毛利润,当时,S最大,即年产量是750吨时,所获毛利润最大.
14.答案:15
m
解析:如答图,三块矩形区域的面积相等,矩形AEFD面积是矩形BCFE面积的2倍,.设m,m,则m,,矩形区域ABCD的面积.,.二次项系数当时,S有最大值.
15.答案:解:(1)根据题意,得cm,cm.
在中,cm,cm.
若是直角三角形,则或.
①当时,,即,解得;
②当时,,即,解得.
综上所述,当或时,是直角三角形.
(2)如答图,过点P作于点M,则,
,
,
y与t的函数关系式为.
,四边形APQC的面积有最小值,最小值为.
——基础提升练(6)实际问题与二次函数
提升练
1.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,则能获取的最大利润是(
)
A.600元
B.625元
C.650元
D.675元
2.一家电脑公司推出一款新型电脑.投放市场以来前3个月的利润情况如图所示,该图可以近似看作抛物线的一部分.则该公司在经营此款电脑过程中,利润最大的月份是(
)
A.第5个月
B.第6个月
C.第7个月
D.第8个月
3.如图,点是线段上的一动点,,分别以和为一边作正方形,用表示这两个正方形的面积之和,下列判断正确的是(
)
A.当是的中点时,最小
B.当是的中点时,最大
C.当是的三等分点时,最小
D.当是的三等分点时,最大
4.如图是抛物线形拱桥,当拱顶高离水面2
m时,水面宽4
m,水面下降2.5
m,水面宽度增加(
)
A.1
m
B.2
m
C.3
m
D.6
m
5.某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天的销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图,则每天的最大利润是(
)
A.180元
B.220元
C.190元
D.200元
6.某宾馆共有80间客房,宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足.若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间的定价确定为(
)
A.252元/间
B.256元/间
C.258元/间
D.260元/间
7.一位篮球运动员在距离篮圈中心水平距离4
m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5
m时,达到最大高度3.5
m,然后准确落入篮筐内.已知篮圈中心距离地面的高度为3.05
m,在如图的平面直角坐标系中,下列说法正确的是(
)
A.此抛物线对应的函数表达式是
B.篮圈中心的坐标是
C.此抛物线的顶点坐标是
D.篮球出手时离地面的高度是2
m
8.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.则该企业每天可以获得的最大销售利润是(
)
A.5500元
B.5000元
C.4800元
D.4500元
9.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃.臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”与加工煎炸时间(单位:分钟)近似满足的函数关系为:(,是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为(
)
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
10.如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图像,其中曲线段AB是以B为顶点的抛物线的一部分.下列说法不正确的是(
)
A.25
min~50
min,王阿姨步行的路程为800
m
B.线段CD对应的函数表达式为
C.5
min~20
min,王阿姨步行速度由慢到快
D.曲线段AB对应的函数表达式为
11.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是__________米.
12.如图,在中,mm,mm,动点P从点A开始沿边AB向B以2
mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4
mm/s的速度移动(不与点C重合).如果P,Q分别从A,B同时出发,那么经过__________s,四边形APQC的面积最小.
13.某种产品的年产量不超过1000吨,该产品的年产量(单位:吨)与费用(单位:万元)之间的函数的图象是顶点在原点的抛物线的一部分〔如图(1)〕;该产品的年销售量(单位:吨)与销售单价(单位:万元/吨)之间的函数图象是线段〔如图(2)〕.若生产出的产品都能在当年销售完,则年产量是___________吨时,所获毛利润最大.(毛利润=销售额-费用)
14.为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为60
m的篱笆围成了如图的①②③三块矩形区域,而且这三块矩形区域的面积相等,则BC长为__________时,能围成的矩形区域ABCD的面积最大.
15.如图,是边长为3cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1
cm/s.当点P到达点B时,P,Q两点停止运动.设点P的运动时间为t(s),解答下列问题:
(1)当t为何值时,是直角三角形?
(2)设四边形APQC的面积为y(),求y()与t(s)的函数关系式.是否存在某一时刻t(s),使得四边形APQC的面积有最值?若存在,求出最值.
答案以及解析
1.答案:B
解析:设降价x元时获取利润y元,则有.,当时,.
2.答案:C
解析:图象过原点,故可设二次函数表达式为.由图可知,图象过点,代入解得,.即该公司在经营此款电脑过程中,利润最大的月份是第7个月.故选C.
3.答案:A
解析:设,则,根据题意,得,所以当时,取得最小值,此时,是的中点.故选A.
4.答案:B
解析:如答图,建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB的中点O且通过点C,则通过画图可知O为原点,抛物线以y轴为对称轴.根据题意,知抛物线顶点C的坐标为,设抛物线对应的函数表达式为,把点A的坐标代入,得,得,抛物线对应的函数表达式为,当时,
,解得,水面下降2.5m,水面宽度增加2
m.故选B.
5.答案:D
解析:设,由图像可知,解得.设销售利润为p元,根据题意,得.p有最大值.当时,.即当销售单价为20元/千克时,每天可获得最大利润是200元.故选D.
6.答案:B
解析:设每天的利润为W元,根据题意,得.当时,不是整数,舍去,当或时,函数取得最大值.又想让客人得到实惠,宾馆应将房间定价确定为256元/间时,才能获得最大利润.故选B.
7.答案:A
解析:抛物线的顶点坐标为可设抛物线对应的函数表达式为篮圈中心在抛物线上,将它的坐标代入上式,得,,选项A正确;由题图可知,篮圈中心的坐标是,选项B错误;由题图可知,此抛物线的顶点坐标是选项C错误;设这次跳投时,球出手处离地面h
m.,当时,这次跳投时,球出手处离地面2.25
m,选项D错误.故选A.
8.答案:D
解析:设销售单价为x元,利润为y元,由题意可得,抛物线开口向下.,对称轴是直线,当时,y有最大值为4500,即销售单价为80元时,每天的销售利润最大,最大利润是4500元.故选D.
9.答案:C
解析:本题考查二次函数的应用.将图象中的三个点代入函数关系中得,,解得,所以函数关系式为.由题意可知,加工煎炸臭豆腐的最佳时间应为抛物线顶点的横坐标,则当分钟时,为最佳时间,故选C.
10.答案:C
解析:25
min~50
min,王阿姨步行的路程为(m),A不符合题意;设线段CD对应的函数表达式为,把点的坐标分别代入,得解得线段CD对应的函数表达式为,B不符合题意;在点A的速度为,在点B的速度为,5
min~20
min,王阿姨步行速度由快到慢,C符合题意;当时,由图像可得m,将代入得,D不符合题意.故选C.
11.答案:4
解析:水在空中划出的曲线是抛物线的一部分,喷水的最大高度就是水在空中划出的抛物线的顶点坐标的纵坐标.顶点坐标为喷水的最大高度为4米.
12.答案:3
解析:设P,Q同时出发后经过的时间为t
s,四边形APQC的面积为S,则有.因为,所以当s时,S取得最小值.
13.答案:750
解析:设年产量为x吨,费用为y万元,销售单价为z万元/吨,则由题图(1)得y与x的函数表达式为.由题图(2)得z与x的函数表达式为.设毛利润为S(万元),则毛利润,当时,S最大,即年产量是750吨时,所获毛利润最大.
14.答案:15
m
解析:如答图,三块矩形区域的面积相等,矩形AEFD面积是矩形BCFE面积的2倍,.设m,m,则m,,矩形区域ABCD的面积.,.二次项系数当时,S有最大值.
15.答案:解:(1)根据题意,得cm,cm.
在中,cm,cm.
若是直角三角形,则或.
①当时,,即,解得;
②当时,,即,解得.
综上所述,当或时,是直角三角形.
(2)如答图,过点P作于点M,则,
,
,
y与t的函数关系式为.
,四边形APQC的面积有最小值,最小值为.
同课章节目录
