2021-2022学年数学人教版九年级上册22.3 实际问题与二次函数(5)基础练(Word版含答案)
文档属性
| 名称 | 2021-2022学年数学人教版九年级上册22.3 实际问题与二次函数(5)基础练(Word版含答案) | 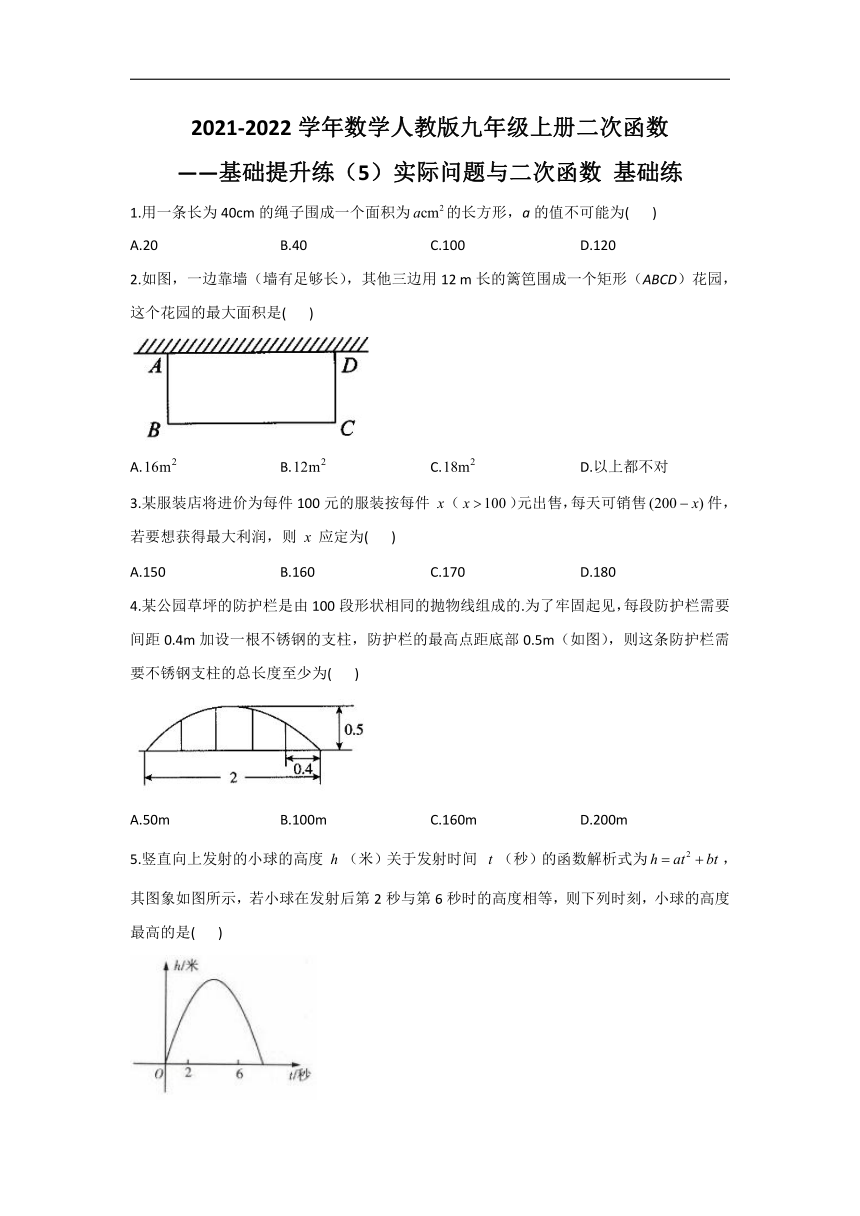 | |
| 格式 | docx | ||
| 文件大小 | 313.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 18:02:46 | ||
图片预览


文档简介
2021-2022学年数学人教版九年级上册二次函数
——基础提升练(5)实际问题与二次函数
基础练
1.用一条长为40cm的绳子围成一个面积为的长方形,a的值不可能为(
)
A.20
B.40
C.100
D.120
2.如图,一边靠墙(墙有足够长),其他三边用12
m长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是(
)
A.
B.
C.
D.以上都不对
3.某服装店将进价为每件100元的服装按每件()元出售,每天可销售件,若要想获得最大利润,则应定为(
)
A.150
B.160
C.170
D.180
4.某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段防护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.50m
B.100m
C.160m
D.200m
5.竖直向上发射的小球的高度(米)关于发射时间(秒)的函数解析式为,其图象如图所示,若小球在发射后第2秒与第6秒时的高度相等,则下列时刻,小球的高度最高的是(
)
A.第3秒
B.第3.9秒
C.第4.5秒
D.第6.5秒
6.小明以二次函数的图像为灵感设计了一款杯子,如图为杯子的设计稿,若,则杯子的高CE为(
)
A.14
B.11
C.6
D.3
7.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足,由于某种原因,每件销售价只能满,那么一周可获得的最大利润是(
)
A.1554元
B.1556元
C.1558元
D.1560元
8.如图,在矩形中,,点P从A出发,沿边向B点以1cm/s的速度移动,同时点Q从点B出发,沿以2cm/s的速度移动,分别到达两点就停止运动.则第几秒时,的面积最大(
)
A.2
B.3
C.4
D.5
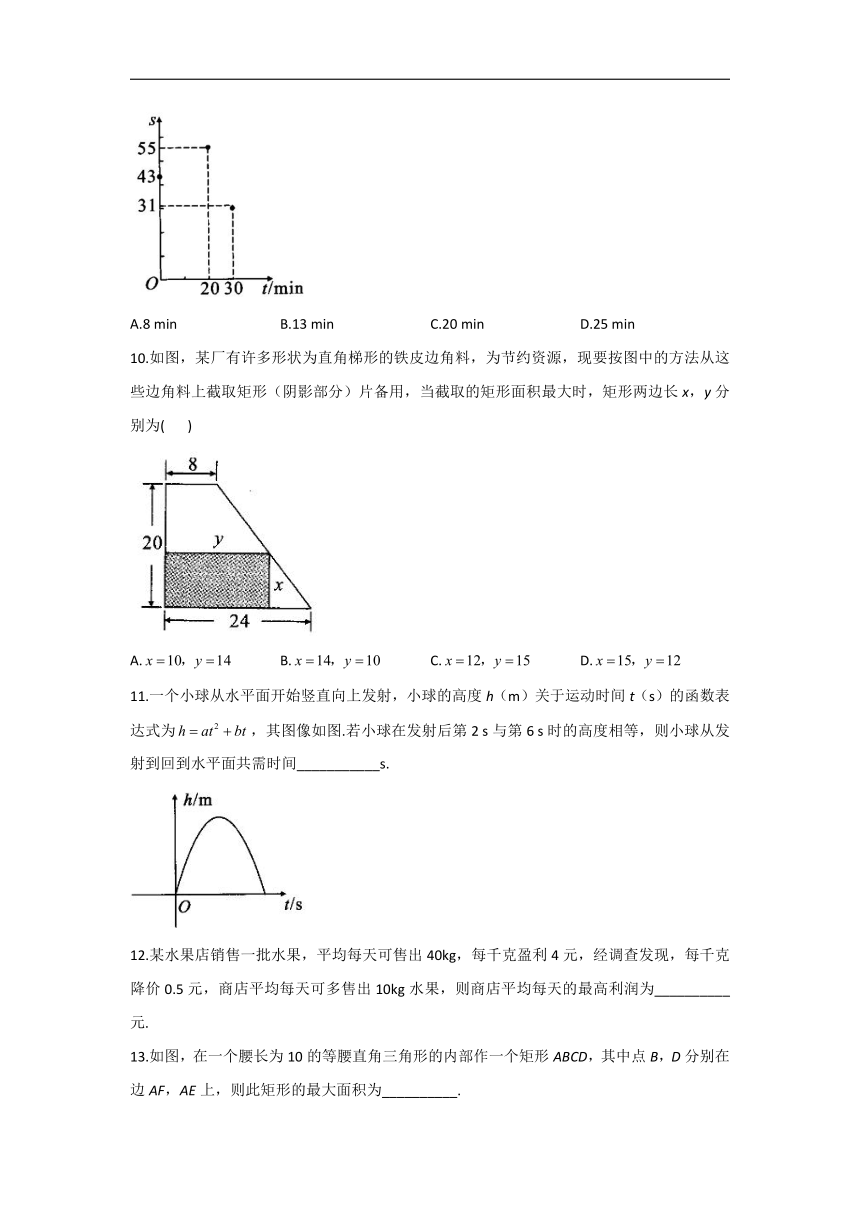
9.心理学家发现:课堂上,学生对概念的接受能力s与提出概念的时间t(以单位:min)之间近似满足函数关系,s值越大,表示接受能力越强.如图,记录了学生学习某概念时t与s的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为(
)
A.8
min
B.13
min
C.20
min
D.25
min
10.如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中的方法从这些边角料上截取矩形(阴影部分)片备用,当截取的矩形面积最大时,矩形两边长x,y分别为(
)
A.
B.
C.
D.
11.一个小球从水平面开始竖直向上发射,小球的高度h(m)关于运动时间t(s)的函数表达式为,其图像如图.若小球在发射后第2
s与第6
s时的高度相等,则小球从发射到回到水平面共需时间___________s.
12.某水果店销售一批水果,平均每天可售出40kg,每千克盈利4元,经调查发现,每千克降价0.5元,商店平均每天可多售出10kg水果,则商店平均每天的最高利润为__________元.
13.如图,在一个腰长为10的等腰直角三角形的内部作一个矩形ABCD,其中点B,D分别在边AF,AE上,则此矩形的最大面积为__________.
14.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端B处有一个喷水孔,喷出的抛物线形水柱在与水池中心A的水平距离为1
m处达到最高点C,高度为3
m,水柱落地点D离水池中心A处3
m,则水管AB的长为__________m.
15.如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,米,米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线对应的函数表达式;
(2)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系式,且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明在这一时段内,需多少小时禁止船只通行.
答案以及解析
1.答案:D
解析:设所围成长方形的长为,则由题意得,,则当时,a取得最大值100.因为,所以a的值不可能为120.故选D.
2.答案:C
解析:设与墙垂直的矩形的边长为x
m,则这个花园的面积是,当时,S取得最大值,此时,即这个花园的最大面积是.故选C.
3.答案:A
解析:设获得的利润为元,由题意,得,所以当时,取得最大值.故选A.
4.答案:C
解析:以一段防护栏的中点为原点,以地面所在直线为x轴,以原点与抛物线顶点连线所在直线为y轴,建立平面直角坐标系,抛物线顶点位于y轴上,则顶点坐标为,可设抛物线的函数表达式为.由于在抛物线上,代入后,得,抛物线的函数表达式为.当时,;当时,.总长度为.故选C.
5.答案:B
解析:由题意,得抛物线的对称轴为直线,.当时,取得最大值,结合选项,知选B.
6.答案:B
解析:抛物线顶点D的坐标为点B的横坐标为,把代入,得.故选B.
7.答案:B
解析:当时,y随x的增大而增大.,当时,y取得最大值,最大值为,即一周可获得的最大利润是1556元.故选B.
8.答案:B
解析:设,得当时面积最大.故选B.
9.答案:B
解析:由题意得函数图像经过点,将此三点的坐标分别代入,得解得函数的表达式为,函数有最大值.当时,s有最大值,即学生接受能力最强.故选B.
10.答案:D
解析:如答图,过点D作于点E,,,得矩形面积当时,S有最大值,此时.故选D.
11.答案:8
解析:由题意可知,小球在发射后第2
s与第6
s时的高度相等,则函数的图像的对称轴,故小球从发射到回到水平面共需时间(s).
12.答案:180
解析:设每千克降价x元,由题意得每天的销售量为(千克).设商店平均每天的利润为W元,由题意,得当时,W取得最大值,最大值为180,即商店平均每天的最高利润为180元.
13.答案:25
解析:是等腰直角三角形,.四边形ABCD是矩形,,.设,矩形ABCD的面积为当时,y有最大值,为25.
14.答案:2.25
解析:以水池中心为原点,竖直安装的水管AB所在的直线为y轴,与水管垂直的直线为x轴建立平面直角坐标系.由于在距水池中心的水平距离为1
m时达到最高,高度为3
m,则设抛物线对应的函数表达式为,将代入,得,解得抛物线对应的函数表达式为.令,则,即水管AB的长为2.25
m.
15.答案:(1)点C到ED的距离是11米,米.
设抛物线对应的函数表达式为.
由题意,得,,解得,.
(2)水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至少为(米).
令,得,,
,解得,(时).
答:在这一时段内,需32小时禁止船只通行.
——基础提升练(5)实际问题与二次函数
基础练
1.用一条长为40cm的绳子围成一个面积为的长方形,a的值不可能为(
)
A.20
B.40
C.100
D.120
2.如图,一边靠墙(墙有足够长),其他三边用12
m长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是(
)
A.
B.
C.
D.以上都不对
3.某服装店将进价为每件100元的服装按每件()元出售,每天可销售件,若要想获得最大利润,则应定为(
)
A.150
B.160
C.170
D.180
4.某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段防护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.50m
B.100m
C.160m
D.200m
5.竖直向上发射的小球的高度(米)关于发射时间(秒)的函数解析式为,其图象如图所示,若小球在发射后第2秒与第6秒时的高度相等,则下列时刻,小球的高度最高的是(
)
A.第3秒
B.第3.9秒
C.第4.5秒
D.第6.5秒
6.小明以二次函数的图像为灵感设计了一款杯子,如图为杯子的设计稿,若,则杯子的高CE为(
)
A.14
B.11
C.6
D.3
7.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足,由于某种原因,每件销售价只能满,那么一周可获得的最大利润是(
)
A.1554元
B.1556元
C.1558元
D.1560元
8.如图,在矩形中,,点P从A出发,沿边向B点以1cm/s的速度移动,同时点Q从点B出发,沿以2cm/s的速度移动,分别到达两点就停止运动.则第几秒时,的面积最大(
)
A.2
B.3
C.4
D.5
9.心理学家发现:课堂上,学生对概念的接受能力s与提出概念的时间t(以单位:min)之间近似满足函数关系,s值越大,表示接受能力越强.如图,记录了学生学习某概念时t与s的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为(
)
A.8
min
B.13
min
C.20
min
D.25
min
10.如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中的方法从这些边角料上截取矩形(阴影部分)片备用,当截取的矩形面积最大时,矩形两边长x,y分别为(
)
A.
B.
C.
D.
11.一个小球从水平面开始竖直向上发射,小球的高度h(m)关于运动时间t(s)的函数表达式为,其图像如图.若小球在发射后第2
s与第6
s时的高度相等,则小球从发射到回到水平面共需时间___________s.
12.某水果店销售一批水果,平均每天可售出40kg,每千克盈利4元,经调查发现,每千克降价0.5元,商店平均每天可多售出10kg水果,则商店平均每天的最高利润为__________元.
13.如图,在一个腰长为10的等腰直角三角形的内部作一个矩形ABCD,其中点B,D分别在边AF,AE上,则此矩形的最大面积为__________.
14.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端B处有一个喷水孔,喷出的抛物线形水柱在与水池中心A的水平距离为1
m处达到最高点C,高度为3
m,水柱落地点D离水池中心A处3
m,则水管AB的长为__________m.
15.如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,米,米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线对应的函数表达式;
(2)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系式,且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明在这一时段内,需多少小时禁止船只通行.
答案以及解析
1.答案:D
解析:设所围成长方形的长为,则由题意得,,则当时,a取得最大值100.因为,所以a的值不可能为120.故选D.
2.答案:C
解析:设与墙垂直的矩形的边长为x
m,则这个花园的面积是,当时,S取得最大值,此时,即这个花园的最大面积是.故选C.
3.答案:A
解析:设获得的利润为元,由题意,得,所以当时,取得最大值.故选A.
4.答案:C
解析:以一段防护栏的中点为原点,以地面所在直线为x轴,以原点与抛物线顶点连线所在直线为y轴,建立平面直角坐标系,抛物线顶点位于y轴上,则顶点坐标为,可设抛物线的函数表达式为.由于在抛物线上,代入后,得,抛物线的函数表达式为.当时,;当时,.总长度为.故选C.
5.答案:B
解析:由题意,得抛物线的对称轴为直线,.当时,取得最大值,结合选项,知选B.
6.答案:B
解析:抛物线顶点D的坐标为点B的横坐标为,把代入,得.故选B.
7.答案:B
解析:当时,y随x的增大而增大.,当时,y取得最大值,最大值为,即一周可获得的最大利润是1556元.故选B.
8.答案:B
解析:设,得当时面积最大.故选B.
9.答案:B
解析:由题意得函数图像经过点,将此三点的坐标分别代入,得解得函数的表达式为,函数有最大值.当时,s有最大值,即学生接受能力最强.故选B.
10.答案:D
解析:如答图,过点D作于点E,,,得矩形面积当时,S有最大值,此时.故选D.
11.答案:8
解析:由题意可知,小球在发射后第2
s与第6
s时的高度相等,则函数的图像的对称轴,故小球从发射到回到水平面共需时间(s).
12.答案:180
解析:设每千克降价x元,由题意得每天的销售量为(千克).设商店平均每天的利润为W元,由题意,得当时,W取得最大值,最大值为180,即商店平均每天的最高利润为180元.
13.答案:25
解析:是等腰直角三角形,.四边形ABCD是矩形,,.设,矩形ABCD的面积为当时,y有最大值,为25.
14.答案:2.25
解析:以水池中心为原点,竖直安装的水管AB所在的直线为y轴,与水管垂直的直线为x轴建立平面直角坐标系.由于在距水池中心的水平距离为1
m时达到最高,高度为3
m,则设抛物线对应的函数表达式为,将代入,得,解得抛物线对应的函数表达式为.令,则,即水管AB的长为2.25
m.
15.答案:(1)点C到ED的距离是11米,米.
设抛物线对应的函数表达式为.
由题意,得,,解得,.
(2)水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至少为(米).
令,得,,
,解得,(时).
答:在这一时段内,需32小时禁止船只通行.
同课章节目录
