2021-2022学年数学北师大版九年级上册3.2用频率估计概率_同步课时作业(word解析版)
文档属性
| 名称 | 2021-2022学年数学北师大版九年级上册3.2用频率估计概率_同步课时作业(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 145.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 08:39:49 | ||
图片预览


文档简介
3.2用频率估计概率—2021-2022学年数学北师大版九年级上册同步课时作业
1.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1
000,则“正面朝上”的频数最接近(
)
A.200
B.300
C.500
D.800
2.某人在做抛掷质地均匀的硬币的试验时,抛掷m次,正面朝上的有n次,正面朝上的频率,则下列说法正确的是(
)
A.f一定等于
B.f一定不等于
C.多抛掷一次,f更接近
D.抛掷次数逐渐增加时,f稳定在附近
3.盒子中有白色乒乓球和黄色乒乓球若干个,某同学每次摸出一个乒乓球,记下它的颜色后放回,如此重复360次,其中摸出白色乒乓球90次,由此估计任意摸出一个乒乓球,摸出的是白色乒乓球的概率为(
)
A.
B.
C.
D.
4.不透明的盒子中有白球和黄球若干个,它们除了颜色外其他完全相同,某同学进行了如下试验:每次摸出一个小球,记下颜色后放回盒中,如此重复400次,其中摸出白球100次.由此估计摸出黄球的概率为(
)
A.
B.
C.
D.
5.下列说法合理的是(
)
A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是
B.抛掷一枚质地均匀的正六面体骰子,出现6的概率是的意思是每6次就有1次掷得6
C.某彩票的中奖机会是,则买100张彩票一定会有2张中奖
D.在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51
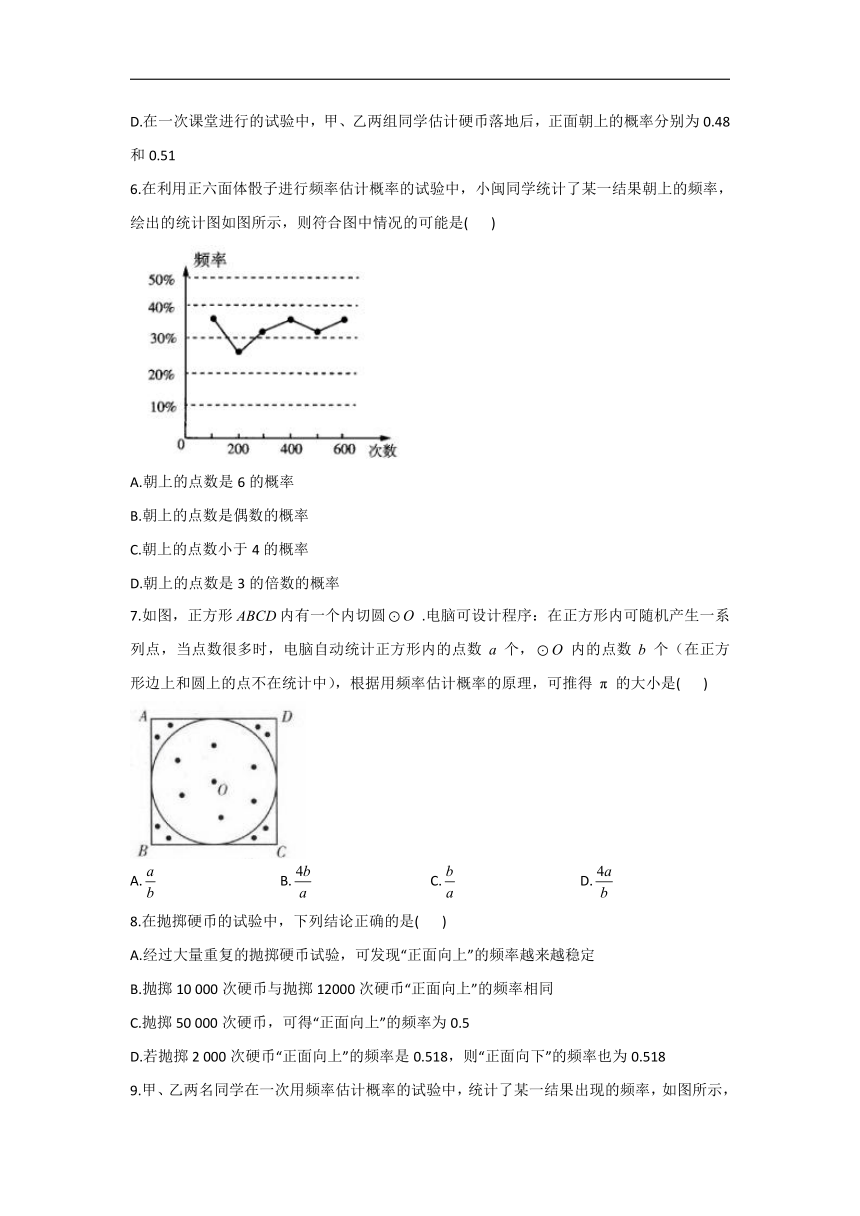
6.在利用正六面体骰子进行频率估计概率的试验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合图中情况的可能是(
)
A.朝上的点数是6的概率
B.朝上的点数是偶数的概率
C.朝上的点数小于4的概率
D.朝上的点数是3的倍数的概率
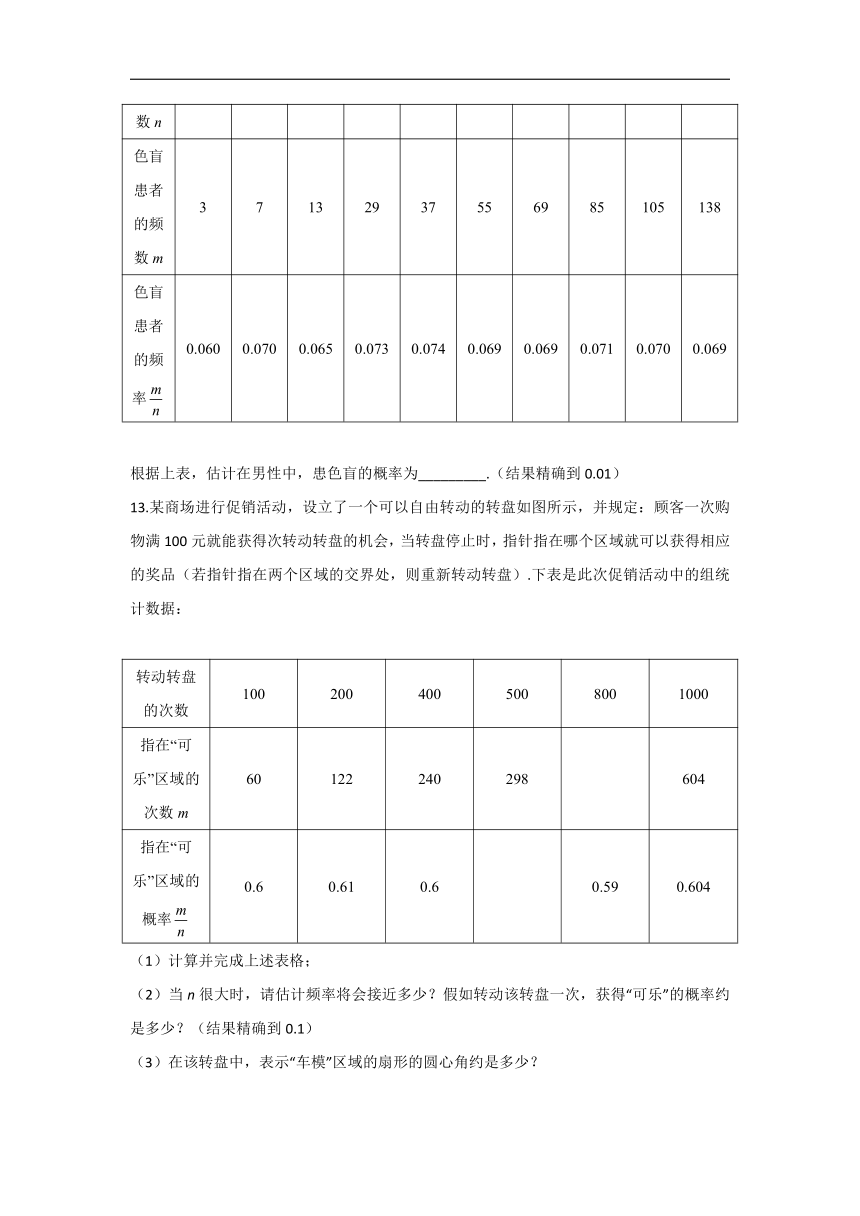
7.如图,正方形内有一个内切圆.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数个,内的点数个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得的大小是(
)
A.
B.
C.
D.
8.在抛掷硬币的试验中,下列结论正确的是(
)
A.经过大量重复的抛掷硬币试验,可发现“正面向上”的频率越来越稳定
B.抛掷10
000次硬币与抛掷12000次硬币“正面向上”的频率相同
C.抛掷50
000次硬币,可得“正面向上”的频率为0.5
D.若抛掷2
000次硬币“正面向上”的频率是0.518,则“正面向下”的频率也为0.518
9.甲、乙两名同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,如图所示,则符合这一结果的试验可能是(
)
A.掷一枚质地均匀的骰子,出现1点的概率
B.掷一枚质地均匀的硬币,出现“正面朝上”的概率
C.从一个装有2个白球和1个红球的不透明袋子中任取一球(白球和红球除颜色外其余完全相同),取到红球的概率
D.从分别写有1,2,3,…,100的100张卡片中任意取一张卡片(卡片除数字外均相同),卡片上的数能被2整除的概率
10.技术变革带来产品质量的提升,某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为_________.(结果要求保留两位小数)
11.为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2
cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为________.
12.色盲是伴X染色体隐性遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取部分体检表,并将统计结果记录如表所示:
抽取的体检表数n
50
100
200
400
500
800
1
000
1
200
1
500
2
000
色盲患者的频数m
3
7
13
29
37
55
69
85
105
138
色盲患者的频率
0.060
0.070
0.065
0.073
0.074
0.069
0.069
0.071
0.070
0.069
根据上表,估计在男性中,患色盲的概率为_________.(结果精确到0.01)
13.某商场进行促销活动,设立了一个可以自由转动的转盘如图所示,并规定:顾客一次购物满100元就能获得次转动转盘的机会,当转盘停止时,指针指在哪个区域就可以获得相应的奖品(若指针指在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的组统计数据:
转动转盘的次数
100
200
400
500
800
1000
指在“可乐”区域的次数m
60
122
240
298
604
指在“可乐”区域的概率
0.6
0.61
0.6
0.59
0.604
(1)计算并完成上述表格;
(2)当n很大时,请估计频率将会接近多少?假如转动该转盘一次,获得“可乐”的概率约是多少?(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少?
答案以及解析
1.答案:C
解析:由题中表格,知随着试验次数的增加,正面朝上的频率逐渐稳定在0.5,所以“正面朝上”的频数最接近.故选C.
2.答案:D
解析:因为一枚硬币只有正、反两面,所以抛掷时正面朝上的概率为.根据频率与概率的关系可知抛掷次数逐渐增加时,f稳定在附近.故选D.
3.答案:A
解析:估计摸出的是白色乒乓球的概率为.故选A.
4.答案:D
解析:估计摸出黄球的概率为.故选D.
5.答案:D
解析:A项,抛图钉的试验中抛掷次数太少,不能把作为钉尖朝上的概率;B项,抛掷一枚质地均匀的正六面体骰子,出现6的概率是,并不是每6次就有1次掷得6;C项,某彩票的中奖机会是,只能说明买100张彩票可能会有2张中奖.故选D.
6.答案:D
解析:从题中统计图可得,该事件发生的可能性在左右,而朝上的点数是6的概率为,朝上的点数是偶数的概率为,朝上的点数小于4的概率为,朝上的点数是3的倍数的概率为,所以D项符合题意.故选D.
7.答案:B
解析:设圆的半径为,则正方形的边长为,根据题意,得,所以.故选B.
8.答案:A
解析:A项,经过大量重复的抛掷硬币试验,可发现“正面向上”的频率越来越稳定,故A项结论正确;B项,频率本身是随机的所以抛掷10000次硬币与抛掷12000次硬币“正面向上”的频率不定相同,故B项结论错误;C项,抛掷50000次硬币,可得“正面向上”的频率约为05,故C项结论错误;D项,若抛掷2000次硬币“正面向上”的频率是0.518,则“正面向下”的频率为0.482,故D项结论错误.故选A.
9.答案:C
解析:掷一枚质地均匀的骰子,出现1点的概率为,故A选项不符合题意;掷一枚质地均匀的硬币,出现“正面朝上”的概率为,故B选项不符合题意;从一个装有2个白球和1个红球的不透明袋子中任取一球,取到红球的概率是,故C选项符合题意;任意取一张卡片,卡片上的数能被2整除的概率为,故D选项不符合题意.故选C.
10.答案:0.99
解析:大量重复试验时,事件发生的频率逐渐稳定到某个常数附近,可以用这个常数估计这个事件发生的概率,故可以用该产品合格的频率0.9911来估计该产品合格的概率为0.99.
11.答案:2.4
解析:因为正方形的二维码的边长为2
cm,所以正方形二维码的面积为4
cm?.由题意得,黑色部分的面积占正方形二维码面积的60%,所以黑色部分的总面积约为(cm?)
12.答案:0.07
解析:观察题中表格发现,随着抽取人数的增多,男性患色盲的频率逐渐稳定在0.07附近,故可估计男性中,患色盲的概率为0.07.
13.答案:(1)完成表格如下:
转动转盘的次数
100
200
400
500
800
1000
指在“可乐”区域的次数m
60
122
240
298
472
604
指在“可乐”区域的频率
0.6
0.61
0.6
0.596
0.59
0.604
(2)根据(1)中表格,知当n很大时,频率将会接近0.6.
用频率估计概率,知获得“可乐”的概率约是0.6.
(3)由(2)可知获得“车模”的概率约是0.4,
所以表示“车模”区域的扇形的圆心角约是.
1.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1
000,则“正面朝上”的频数最接近(
)
A.200
B.300
C.500
D.800
2.某人在做抛掷质地均匀的硬币的试验时,抛掷m次,正面朝上的有n次,正面朝上的频率,则下列说法正确的是(
)
A.f一定等于
B.f一定不等于
C.多抛掷一次,f更接近
D.抛掷次数逐渐增加时,f稳定在附近
3.盒子中有白色乒乓球和黄色乒乓球若干个,某同学每次摸出一个乒乓球,记下它的颜色后放回,如此重复360次,其中摸出白色乒乓球90次,由此估计任意摸出一个乒乓球,摸出的是白色乒乓球的概率为(
)
A.
B.
C.
D.
4.不透明的盒子中有白球和黄球若干个,它们除了颜色外其他完全相同,某同学进行了如下试验:每次摸出一个小球,记下颜色后放回盒中,如此重复400次,其中摸出白球100次.由此估计摸出黄球的概率为(
)
A.
B.
C.
D.
5.下列说法合理的是(
)
A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是
B.抛掷一枚质地均匀的正六面体骰子,出现6的概率是的意思是每6次就有1次掷得6
C.某彩票的中奖机会是,则买100张彩票一定会有2张中奖
D.在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51
6.在利用正六面体骰子进行频率估计概率的试验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合图中情况的可能是(
)
A.朝上的点数是6的概率
B.朝上的点数是偶数的概率
C.朝上的点数小于4的概率
D.朝上的点数是3的倍数的概率
7.如图,正方形内有一个内切圆.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数个,内的点数个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得的大小是(
)
A.
B.
C.
D.
8.在抛掷硬币的试验中,下列结论正确的是(
)
A.经过大量重复的抛掷硬币试验,可发现“正面向上”的频率越来越稳定
B.抛掷10
000次硬币与抛掷12000次硬币“正面向上”的频率相同
C.抛掷50
000次硬币,可得“正面向上”的频率为0.5
D.若抛掷2
000次硬币“正面向上”的频率是0.518,则“正面向下”的频率也为0.518
9.甲、乙两名同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,如图所示,则符合这一结果的试验可能是(
)
A.掷一枚质地均匀的骰子,出现1点的概率
B.掷一枚质地均匀的硬币,出现“正面朝上”的概率
C.从一个装有2个白球和1个红球的不透明袋子中任取一球(白球和红球除颜色外其余完全相同),取到红球的概率
D.从分别写有1,2,3,…,100的100张卡片中任意取一张卡片(卡片除数字外均相同),卡片上的数能被2整除的概率
10.技术变革带来产品质量的提升,某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为_________.(结果要求保留两位小数)
11.为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2
cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为________.
12.色盲是伴X染色体隐性遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取部分体检表,并将统计结果记录如表所示:
抽取的体检表数n
50
100
200
400
500
800
1
000
1
200
1
500
2
000
色盲患者的频数m
3
7
13
29
37
55
69
85
105
138
色盲患者的频率
0.060
0.070
0.065
0.073
0.074
0.069
0.069
0.071
0.070
0.069
根据上表,估计在男性中,患色盲的概率为_________.(结果精确到0.01)
13.某商场进行促销活动,设立了一个可以自由转动的转盘如图所示,并规定:顾客一次购物满100元就能获得次转动转盘的机会,当转盘停止时,指针指在哪个区域就可以获得相应的奖品(若指针指在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的组统计数据:
转动转盘的次数
100
200
400
500
800
1000
指在“可乐”区域的次数m
60
122
240
298
604
指在“可乐”区域的概率
0.6
0.61
0.6
0.59
0.604
(1)计算并完成上述表格;
(2)当n很大时,请估计频率将会接近多少?假如转动该转盘一次,获得“可乐”的概率约是多少?(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少?
答案以及解析
1.答案:C
解析:由题中表格,知随着试验次数的增加,正面朝上的频率逐渐稳定在0.5,所以“正面朝上”的频数最接近.故选C.
2.答案:D
解析:因为一枚硬币只有正、反两面,所以抛掷时正面朝上的概率为.根据频率与概率的关系可知抛掷次数逐渐增加时,f稳定在附近.故选D.
3.答案:A
解析:估计摸出的是白色乒乓球的概率为.故选A.
4.答案:D
解析:估计摸出黄球的概率为.故选D.
5.答案:D
解析:A项,抛图钉的试验中抛掷次数太少,不能把作为钉尖朝上的概率;B项,抛掷一枚质地均匀的正六面体骰子,出现6的概率是,并不是每6次就有1次掷得6;C项,某彩票的中奖机会是,只能说明买100张彩票可能会有2张中奖.故选D.
6.答案:D
解析:从题中统计图可得,该事件发生的可能性在左右,而朝上的点数是6的概率为,朝上的点数是偶数的概率为,朝上的点数小于4的概率为,朝上的点数是3的倍数的概率为,所以D项符合题意.故选D.
7.答案:B
解析:设圆的半径为,则正方形的边长为,根据题意,得,所以.故选B.
8.答案:A
解析:A项,经过大量重复的抛掷硬币试验,可发现“正面向上”的频率越来越稳定,故A项结论正确;B项,频率本身是随机的所以抛掷10000次硬币与抛掷12000次硬币“正面向上”的频率不定相同,故B项结论错误;C项,抛掷50000次硬币,可得“正面向上”的频率约为05,故C项结论错误;D项,若抛掷2000次硬币“正面向上”的频率是0.518,则“正面向下”的频率为0.482,故D项结论错误.故选A.
9.答案:C
解析:掷一枚质地均匀的骰子,出现1点的概率为,故A选项不符合题意;掷一枚质地均匀的硬币,出现“正面朝上”的概率为,故B选项不符合题意;从一个装有2个白球和1个红球的不透明袋子中任取一球,取到红球的概率是,故C选项符合题意;任意取一张卡片,卡片上的数能被2整除的概率为,故D选项不符合题意.故选C.
10.答案:0.99
解析:大量重复试验时,事件发生的频率逐渐稳定到某个常数附近,可以用这个常数估计这个事件发生的概率,故可以用该产品合格的频率0.9911来估计该产品合格的概率为0.99.
11.答案:2.4
解析:因为正方形的二维码的边长为2
cm,所以正方形二维码的面积为4
cm?.由题意得,黑色部分的面积占正方形二维码面积的60%,所以黑色部分的总面积约为(cm?)
12.答案:0.07
解析:观察题中表格发现,随着抽取人数的增多,男性患色盲的频率逐渐稳定在0.07附近,故可估计男性中,患色盲的概率为0.07.
13.答案:(1)完成表格如下:
转动转盘的次数
100
200
400
500
800
1000
指在“可乐”区域的次数m
60
122
240
298
472
604
指在“可乐”区域的频率
0.6
0.61
0.6
0.596
0.59
0.604
(2)根据(1)中表格,知当n很大时,频率将会接近0.6.
用频率估计概率,知获得“可乐”的概率约是0.6.
(3)由(2)可知获得“车模”的概率约是0.4,
所以表示“车模”区域的扇形的圆心角约是.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
