3.2.2双曲线的简单几何性质(教案)-高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.2.2双曲线的简单几何性质(教案)-高中数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | doc | ||
| 文件大小 | 10.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 17:12:41 | ||
图片预览


文档简介
第三章
圆锥曲线的方程
3.2
双曲线
3.2.2
双曲线的简单几何性质
教学设计
一、教学目标
1.
掌握双曲线的简单几何性质.
2.
能够运用双曲线的几何性质解决双曲线的综合问题.
二、教学重难点
1.
教学重点
双曲线的简单几何性质.
2.
教学难点
双曲线的渐近线.
三、教学过程
(一)新课导入
复习:
1.
双曲线的定义:一般地,我们把平面内与两个定点,的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
2.
双曲线的标准方程:
(1)焦点在x轴上的双曲线的标准方程是,焦点分别是,,且.
(2)焦点在y轴上的双曲线的标准方程是,焦点分别是,,且.
思考:类比椭圆的几何性质,来研究双曲线的几何性质.
(二)探索新知
1.
范围
由方程可得,
于是,双曲线上点的坐标都适合不等式,即.
所以,或;.
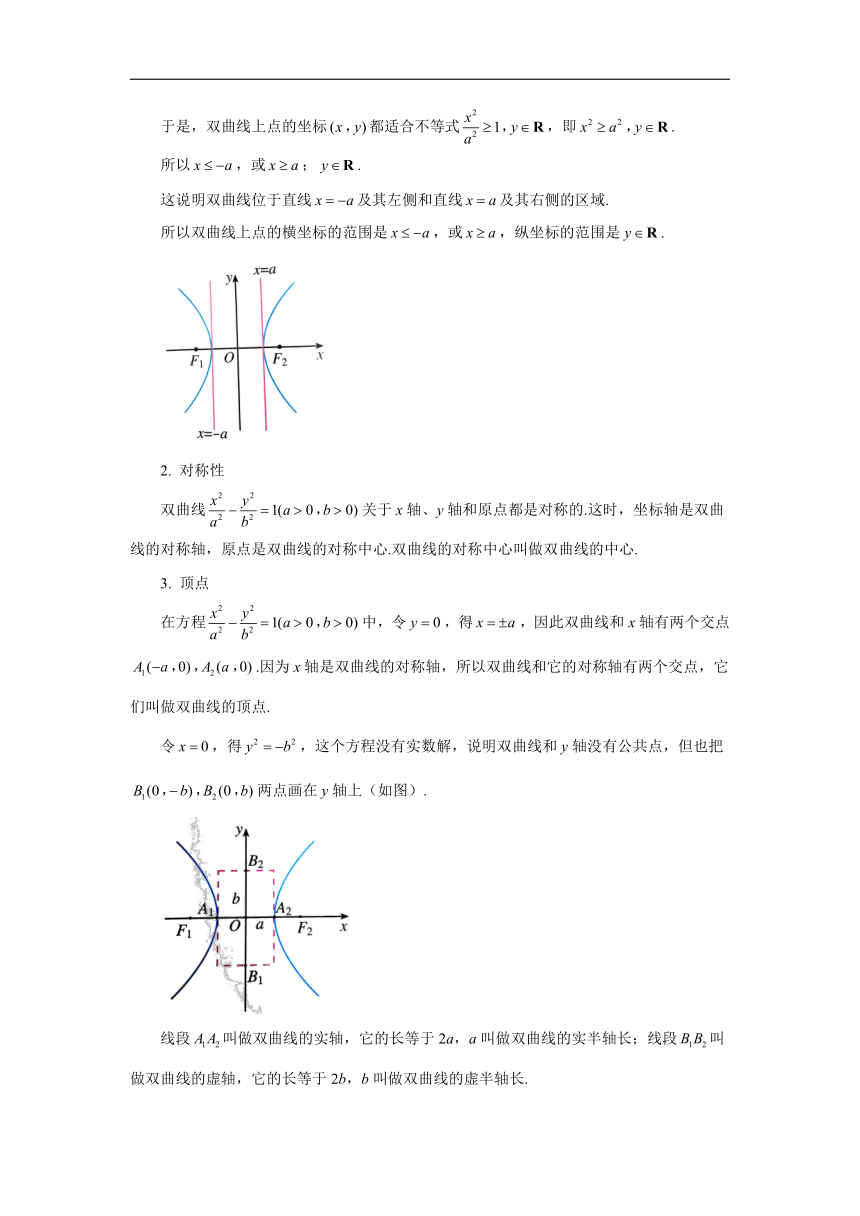
这说明双曲线位于直线及其左侧和直线及其右侧的区域.
所以双曲线上点的横坐标的范围是,或,纵坐标的范围是.
2.
对称性
双曲线关于x轴、y轴和原点都是对称的.这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心.
3.
顶点
在方程中,令,得,因此双曲线和x轴有两个交点.因为x轴是双曲线的对称轴,所以双曲线和它的对称轴有两个交点,它们叫做双曲线的顶点.
令,得,这个方程没有实数解,说明双曲线和y轴没有公共点,但也把两点画在y轴上(如图).
线段叫做双曲线的实轴,它的长等于2a,a叫做双曲线的实半轴长;线段叫做双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.
4.
渐近线
一般地,双曲线的两支向外延伸时,与两条直线逐渐接近,我们把这两条直线叫做双曲线的渐近线.实际上,双曲线与它的渐近线无限接近,但永远不相交.
在双曲线方程中,如果,那么方程变为,此时双曲线的实轴和虚轴的长都等于2a.
这时,四条直线围成正方形,渐近线方程为,它们互相垂直,并且平分双曲线的实轴和虚轴所成的角.实轴和虚轴等长的双曲线叫做等轴双曲线.
5.
离心率
双曲线的焦距和实轴长的比,叫做双曲线的离心率.因为,所以双曲线的离心率.
双曲线的离心率刻画了双曲线的“张口”大小.
例1
求双曲线的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
解:把双曲线的方程化为标准方程.
由此可知,实半轴长,虚半轴长;,焦点坐标是;离心率;渐近线方程为.
例2
动点与定点的距离和它到定直线的距离的比是常数,求动点M的轨迹.
解:设d是点M到直线l的距离,根据题意,动点M的轨迹就是点的集合,由此得.
将上式两边平方,并化简,得,即.
所以,点M的轨迹是焦点在x轴上,实轴长为6、虚轴长为的双曲线.
例3
如图,过双曲线的右焦点,倾斜角为的直线交双曲线于A,B两点,求.
解:由双曲线的标准方程可知,双曲线的焦点分别为.
因为直线AB的倾斜角是,且经过右焦点,所以直线AB的方程为.①
由消去y,得.
解方程,得.
将的值分别代入①,得.
于是,A,B两点的坐标分别为.
所以.
(三)课堂练习
1.双曲线的虚轴长是实轴长的2倍,则等于(
)
A.
B.
C.4
D.
答案:A
解析:双曲线方程化为标准形式:,则有,.由题设知,解得.
2.等轴双曲线的一个焦点是,则其标准方程为(
)
A.
B.
C.
D.
答案:D
解析:等轴双曲线的一个焦点为,,即双曲线的标准方程为.
3.已知是双曲线上不同的三点,且连线经过坐标原点,若直线的斜率乘积为,则该双曲线的离心率为(
)
A.
B.
C.
D.
答案:D
解析:设,根据对称性,知,
所以.因为在双曲线上,所以,两式相减,得,所以,所以.
4.已知双曲线的渐近线方程为,且焦距是,则双曲线的方程为______________.
答案:或
解析:由题意,设双曲线方程为.
若,则.由题设知,所以,故所求双曲线的方程为.
若,则.由,得,故所求双曲线的方程为.
综上,所求双曲线的方程为或.
5.分别求满足下列条件的双曲线的标准方程:
(1)以圆与坐标轴的交点分别作为双曲线的一个焦点和一个顶点;
(2)焦点在轴上,渐近线方程为,且顶点到渐近线的距离为1;
(3)焦点为,且与双曲线有相同的渐近线.
答案:(1)对圆的方程,令,得,
解得,即圆与轴的两个交点分别为.
令,得,此方程无解,即圆与轴没有交点.
因此点为双曲线的右顶点,点为双曲线的右焦点.
设双曲线的标准方程为,
则,所以,
从而双曲线的标准方程为.
(2)由焦点在轴上,可设双曲线的标准方程为,则渐近线方程为,所以.
由顶点到渐近线的距离为1,得,
所以.
从而双曲线的标准方程为.
(3)设所求双曲线的标准方程为.
由双曲线的一个焦点为,可知,且,得,
则双曲线的标准方程为.
(四)小结作业
小结:双曲线的简单几何性质.
作业:
四、板书设计
3.2.2
双曲线的简单几何性质
双曲线的简单几何性质:
1.
范围:双曲线上点的横坐标的范围是,或,纵坐标的范围是.
2.
对称性:关于x轴、y轴和原点都是对称的.坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心.
3.
顶点:线段叫做双曲线的实轴,它的长等于2a,a叫做双曲线的实半轴长;线段叫做双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.
4.
渐近线:.
实轴和虚轴等长的双曲线叫做等轴双曲线.
5.
离心率:.
圆锥曲线的方程
3.2
双曲线
3.2.2
双曲线的简单几何性质
教学设计
一、教学目标
1.
掌握双曲线的简单几何性质.
2.
能够运用双曲线的几何性质解决双曲线的综合问题.
二、教学重难点
1.
教学重点
双曲线的简单几何性质.
2.
教学难点
双曲线的渐近线.
三、教学过程
(一)新课导入
复习:
1.
双曲线的定义:一般地,我们把平面内与两个定点,的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
2.
双曲线的标准方程:
(1)焦点在x轴上的双曲线的标准方程是,焦点分别是,,且.
(2)焦点在y轴上的双曲线的标准方程是,焦点分别是,,且.
思考:类比椭圆的几何性质,来研究双曲线的几何性质.
(二)探索新知
1.
范围
由方程可得,
于是,双曲线上点的坐标都适合不等式,即.
所以,或;.
这说明双曲线位于直线及其左侧和直线及其右侧的区域.
所以双曲线上点的横坐标的范围是,或,纵坐标的范围是.
2.
对称性
双曲线关于x轴、y轴和原点都是对称的.这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心.
3.
顶点
在方程中,令,得,因此双曲线和x轴有两个交点.因为x轴是双曲线的对称轴,所以双曲线和它的对称轴有两个交点,它们叫做双曲线的顶点.
令,得,这个方程没有实数解,说明双曲线和y轴没有公共点,但也把两点画在y轴上(如图).
线段叫做双曲线的实轴,它的长等于2a,a叫做双曲线的实半轴长;线段叫做双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.
4.
渐近线
一般地,双曲线的两支向外延伸时,与两条直线逐渐接近,我们把这两条直线叫做双曲线的渐近线.实际上,双曲线与它的渐近线无限接近,但永远不相交.
在双曲线方程中,如果,那么方程变为,此时双曲线的实轴和虚轴的长都等于2a.
这时,四条直线围成正方形,渐近线方程为,它们互相垂直,并且平分双曲线的实轴和虚轴所成的角.实轴和虚轴等长的双曲线叫做等轴双曲线.
5.
离心率
双曲线的焦距和实轴长的比,叫做双曲线的离心率.因为,所以双曲线的离心率.
双曲线的离心率刻画了双曲线的“张口”大小.
例1
求双曲线的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
解:把双曲线的方程化为标准方程.
由此可知,实半轴长,虚半轴长;,焦点坐标是;离心率;渐近线方程为.
例2
动点与定点的距离和它到定直线的距离的比是常数,求动点M的轨迹.
解:设d是点M到直线l的距离,根据题意,动点M的轨迹就是点的集合,由此得.
将上式两边平方,并化简,得,即.
所以,点M的轨迹是焦点在x轴上,实轴长为6、虚轴长为的双曲线.
例3
如图,过双曲线的右焦点,倾斜角为的直线交双曲线于A,B两点,求.
解:由双曲线的标准方程可知,双曲线的焦点分别为.
因为直线AB的倾斜角是,且经过右焦点,所以直线AB的方程为.①
由消去y,得.
解方程,得.
将的值分别代入①,得.
于是,A,B两点的坐标分别为.
所以.
(三)课堂练习
1.双曲线的虚轴长是实轴长的2倍,则等于(
)
A.
B.
C.4
D.
答案:A
解析:双曲线方程化为标准形式:,则有,.由题设知,解得.
2.等轴双曲线的一个焦点是,则其标准方程为(
)
A.
B.
C.
D.
答案:D
解析:等轴双曲线的一个焦点为,,即双曲线的标准方程为.
3.已知是双曲线上不同的三点,且连线经过坐标原点,若直线的斜率乘积为,则该双曲线的离心率为(
)
A.
B.
C.
D.
答案:D
解析:设,根据对称性,知,
所以.因为在双曲线上,所以,两式相减,得,所以,所以.
4.已知双曲线的渐近线方程为,且焦距是,则双曲线的方程为______________.
答案:或
解析:由题意,设双曲线方程为.
若,则.由题设知,所以,故所求双曲线的方程为.
若,则.由,得,故所求双曲线的方程为.
综上,所求双曲线的方程为或.
5.分别求满足下列条件的双曲线的标准方程:
(1)以圆与坐标轴的交点分别作为双曲线的一个焦点和一个顶点;
(2)焦点在轴上,渐近线方程为,且顶点到渐近线的距离为1;
(3)焦点为,且与双曲线有相同的渐近线.
答案:(1)对圆的方程,令,得,
解得,即圆与轴的两个交点分别为.
令,得,此方程无解,即圆与轴没有交点.
因此点为双曲线的右顶点,点为双曲线的右焦点.
设双曲线的标准方程为,
则,所以,
从而双曲线的标准方程为.
(2)由焦点在轴上,可设双曲线的标准方程为,则渐近线方程为,所以.
由顶点到渐近线的距离为1,得,
所以.
从而双曲线的标准方程为.
(3)设所求双曲线的标准方程为.
由双曲线的一个焦点为,可知,且,得,
则双曲线的标准方程为.
(四)小结作业
小结:双曲线的简单几何性质.
作业:
四、板书设计
3.2.2
双曲线的简单几何性质
双曲线的简单几何性质:
1.
范围:双曲线上点的横坐标的范围是,或,纵坐标的范围是.
2.
对称性:关于x轴、y轴和原点都是对称的.坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心.
3.
顶点:线段叫做双曲线的实轴,它的长等于2a,a叫做双曲线的实半轴长;线段叫做双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.
4.
渐近线:.
实轴和虚轴等长的双曲线叫做等轴双曲线.
5.
离心率:.
