(学霸自主提优拔尖)苏教版六年级数学上册第一单元长方体和正方体(知识点、常考题、易错题、拓展题)名师详解与训练二
文档属性
| 名称 | (学霸自主提优拔尖)苏教版六年级数学上册第一单元长方体和正方体(知识点、常考题、易错题、拓展题)名师详解与训练二 |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 20:59:49 | ||
图片预览

文档简介
苏教版六年级上册第一单元:长方体和正方体详解与训练二
一、正方体表面涂色的规律及对应考题
(一)正方体表面涂色的规律
⑴当正方体的棱长是a厘米时,这个正方体可以切成棱长是1厘米的小正方体的个数是n×n×n。如果用N表示这样的个数,那么:N=n×n×n(个)
⑵我们把切开的、棱长是1厘米的小正方体分为四种:
⑶上面四种情况的小正方体都是从原来的正方体中切出来的,所以各部分加起来应当等于切成的总个数。也就是:N=n×n×n=N3+N2+N1+N0
(二)正方体表面涂色规律的对应考题(答案见参考答案)
1.(考点)一个表面涂色的正方体,把这个正方体的每条棱平均分成3份、4份、5……再切成同样大的小正方体。那么每种情况中,分割产生的小正方体的总个数各是多少个?请填写下表。
棱长平均分的份数
3份
4份
5份
……
n份
小正方体的总个数
……
2.(考点)三面涂色的小正方体的个数。
观察发现,3面涂色的小正方体都在大正方体(
)的位置上,正方体有
(
)个顶点,即3面涂色的小正方体有(
)个。
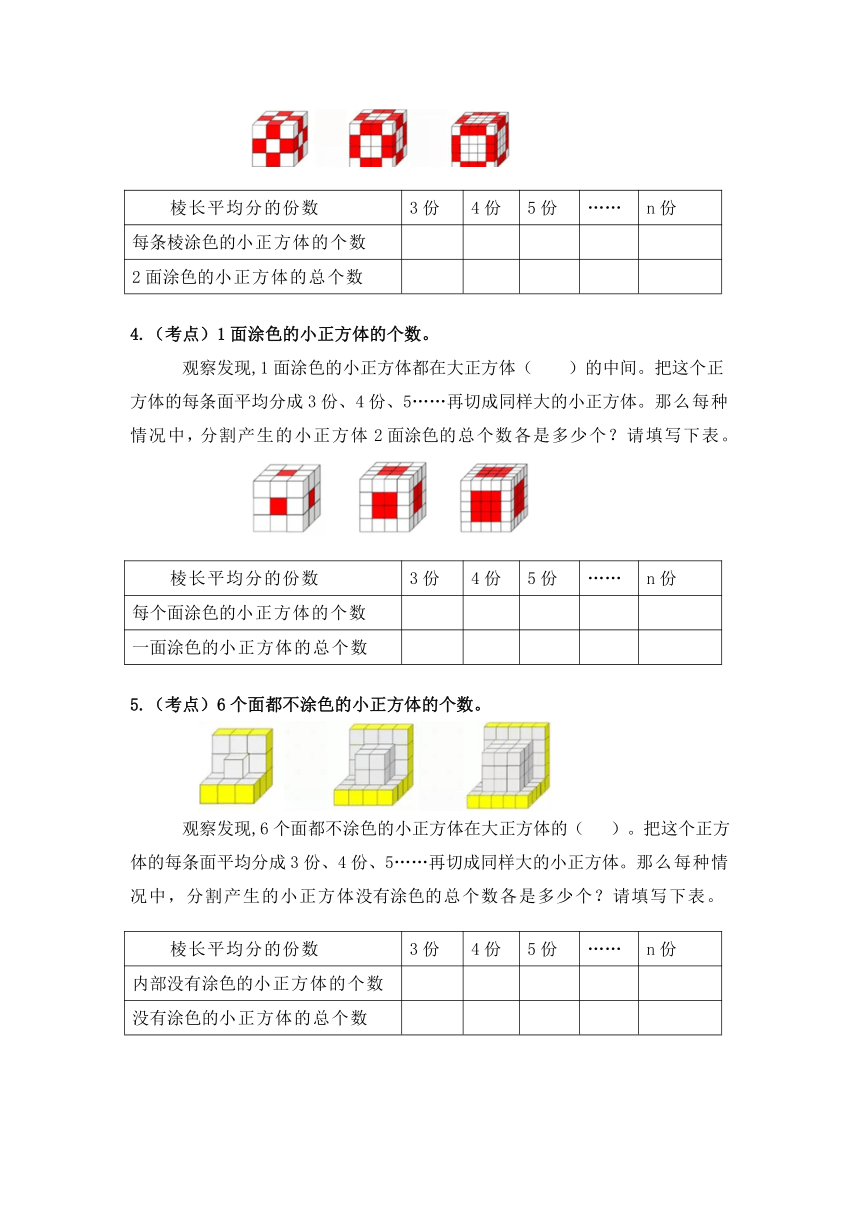
3.(考点)二面涂色的小正方体的个数。
观察发现,2面涂色的小正方体都在大正方体(
)的中间。把这个正方体的每条棱平均分成3份、4份、5……再切成同样大的小正方体。那么每种情况中,分割产生的小正方体2面涂色的总个数各是多少个?请填写下表。
棱长平均分的份数
3份
4份
5份
……
n份
每条棱涂色的小正方体的个数
2面涂色的小正方体的总个数
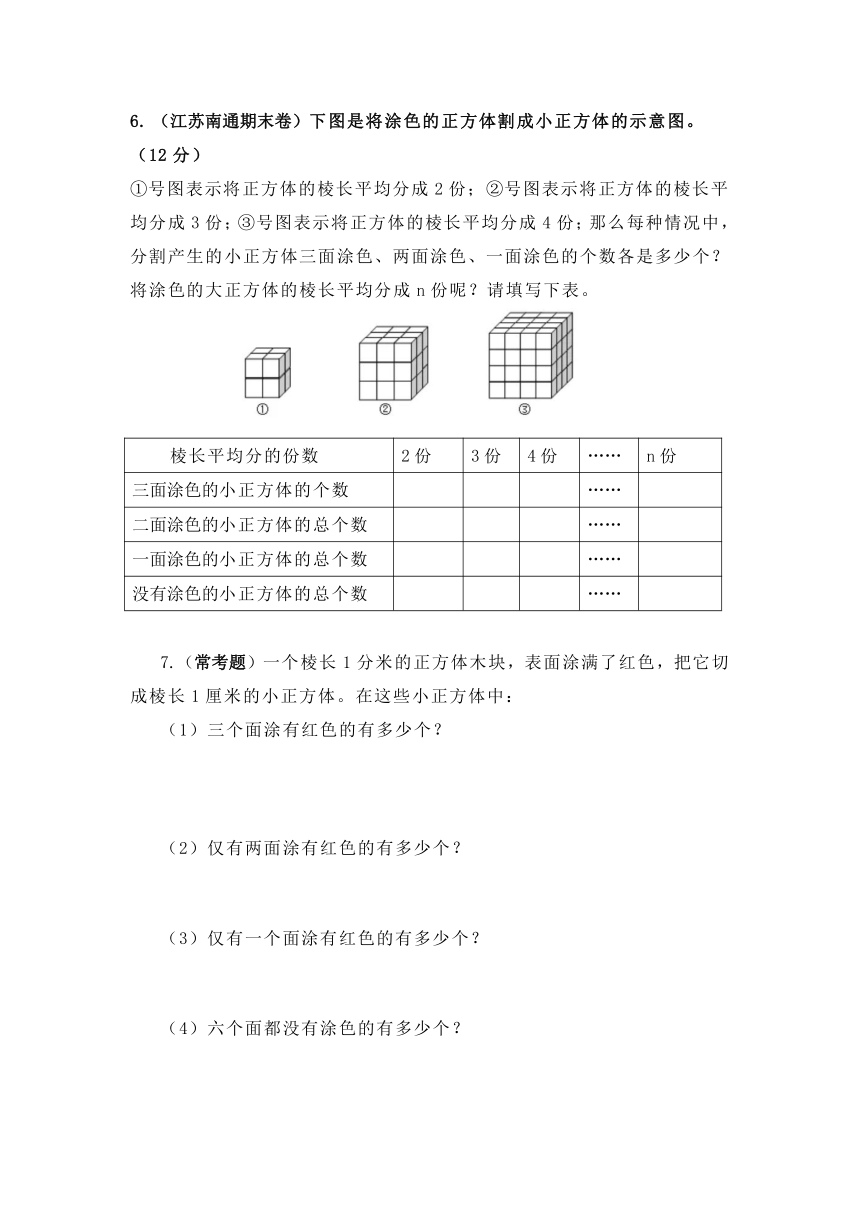
4.(考点)1面涂色的小正方体的个数。
观察发现,1面涂色的小正方体都在大正方体(
)的中间。把这个正方体的每条面平均分成3份、4份、5……再切成同样大的小正方体。那么每种情况中,分割产生的小正方体2面涂色的总个数各是多少个?请填写下表。
棱长平均分的份数
3份
4份
5份
……
n份
每个面涂色的小正方体的个数
一面涂色的小正方体的总个数
5.(考点)6个面都不涂色的小正方体的个数。
观察发现,6个面都不涂色的小正方体在大正方体的(
)。把这个正方体的每条面平均分成3份、4份、5……再切成同样大的小正方体。那么每种情况中,分割产生的小正方体没有涂色的总个数各是多少个?请填写下表。
棱长平均分的份数
3份
4份
5份
……
n份
内部没有涂色的小正方体的个数
没有涂色的小正方体的总个数
(江苏南通期末卷)下图是将涂色的正方体割成小正方体的示意图。
(12分)
①号图表示将正方体的棱长平均分成2份;②号图表示将正方体的棱长平均分成3份;③号图表示将正方体的棱长平均分成4份;那么每种情况中,分割产生的小正方体三面涂色、两面涂色、一面涂色的个数各是多少个?将涂色的大正方体的棱长平均分成n份呢?请填写下表。
棱长平均分的份数
2份
3份
4份
……
n份
三面涂色的小正方体的个数
……
二面涂色的小正方体的总个数
……
一面涂色的小正方体的总个数
……
没有涂色的小正方体的总个数
……
7.(常考题)一个棱长1分米的正方体木块,表面涂满了红色,把它切成棱长1厘米的小正方体。在这些小正方体中:
(1)三个面涂有红色的有多少个??
(2)仅有两面涂有红色的有多少个?????
(3)仅有一个面涂有红色的有多少个??
(4)六个面都没有涂色的有多少个?
第一单元长方体和正方体学霸拓展提优训练二
1.把4个棱长为6厘米的正方体木块拼成1个长方体后,棱长总和减少了多少厘米?
2.一个长方体纸盒的长是宽的3倍,宽比高少5厘米。这个长方体的棱长总和是
92厘米,它的长、宽、高各为多少厘米??(用方程解答)
3.下面的长方形硬纸板各有若干张,从中选三种围成一个长方体,有几种不同的选法?
4.如图是由四个完全一样的正方体拼成的长方体,每个正方体的六个面上分别写有A、B、C、D、E、F六个字母,判断每个正方体相对的面所写的字母。
5.在下图中再添一个小正方形,使它能围成一个正方体。你有多少种不同的方法?
6.亮亮用8个完全相同的小正方体拼成了一个表面积是72平方厘米的大正方体。你能帮亮亮算算原来这8个小正方体的表面积之和是多少吗?
7、下面玻璃缸中已有高1.5dm的水,小红用旁边的水杯装满水往玻璃缸中倒了10次,水会溢出来吗?请通过计算来说明。
8、一个长方体,如果高增加2厘米,就变成了一个正方体(如下图),这时表面积比原来增加48平方厘米。原来长方体的体积是多少立方厘米?
爸爸在院子里用混凝土浇筑了一个无盖的长方体水槽(如图)。?从外面量,水槽长15分米,宽8分米,高5分米,混凝土厚1分米.
(1)这个水槽的容积是多少升?
浇筑这样个水槽需多少混凝土?
10.如图所示,将一个长方体沿长平均截成3段,每段2米,表面积增加了16平方米,原长方体的体积是多少立方米?
11.(常考题)一个涂满红色的正方体,每面等距离切若干刀后,得到一些同样大的小正方体,其中两面涂红的共计60块,那么一面涂红的小正方体有多少块
12.(拓展延伸)一个涂满红色的正方体,每面等距离切若干刀后会得到一些同样大的小正方体,那么:
(1)要想产生54块仅有一面涂有红色的小方块,至少应在各面上切______刀。
(2)要想切出125块大小一样、各面都没有颜色的小正方体,应当在这个大正方体的各面上切______刀(各面切的刀数一样)。
13.[拓展延伸]把一个长为5cm、宽4cm、高6em的长方体木块表面全部涂上红色,然后切成棱长为1厘米的小正方体木块。
(1)切成后,有多少块小正方体木块没有涂上红色?
(2)切开后,有多少块小正方体木块分别有2面、1面被涂有红色?
参考答案与难题详解见下一页
答案就是咱无声的老师
正方体表面涂色的规律及对应考题答案
1.平均切成3份:3×3×3=27(个)
平均切成4份:4×4×4=64(个)
平均切成5份:5×5×5=125(个)
平均切成n份:n?
个
棱平均分的份数
3份
4份
5份
……
n份
小正方体的总个数
3?=27
4?=64
5?=125
……
n?
顶点
8
8
有三面涂色的,都是在顶点处的小方块,一个正方体有8个顶点,所以无论n是多少,有三面涂色的都是8个小方块
观察发现,2面涂色的小正方体都在大正方体(棱
)的中间。
平均分成3份,每条棱上有
1
个,12条棱上共有
12?个。
平均分成4份,每条棱上有
2
个,12条棱上共有
24?
个。
平均分成5份,每条棱上有
3
个,12条棱上共有
36
个。
平均分成n份,每条棱上有(n-2)个,12条棱上共有12(n-2)?个。
棱平均分的份数
3份
4份
5份
……
n份
每条棱涂色的小正方体的个数
3-2=1
4-2=2
5-2=3
……
n-2
2面涂色的小正方体的总个数
1×12=12
2×12=24
3×12=36
……
(n-2)×12
两面涂色的,在每条棱上,除去在顶点处的2个,每条棱上有n-2个,总共12条棱,所以是12(n-2)个;
4.观察发现,1面涂色的小正方体都在大正方体(面)的中间。
平均分成3份,每面有
1
个,6面共有
6
个。
平均分成4份,每面有
4
个,6面共有
24
个。
平均分成5份,每面有
9
个,6面共有
54
个。
平均分成n份,每面有
?(n-2)?
个,6面共有
6(n-2)?个。
棱平均分的份数
3份
4份
5份
…
n份
每个面涂色的小正方体的个数
(3-2)?=1
(4-2)?=4
(5-2)?=9
…
(n-2)?
2面涂色的小正方体的总个数
6×(3-2)?=6
6×(4-2)?=24
6×(5-3)?=54
…
6(n-2)?
一面涂色的,在每个面上,除去每条棱处的,每个面上有(n-2)?个,总共6个面,所以是6(n-2)?个。
观察发现,6个面都不涂色的小正方体在大正方体的(内部)。
平均分成3份:内部棱长为1
,小正方体有
?1
个。
平均分成4份:内部棱长为2
,小正方体有
?8
?个。
平均分成5份:内部棱长为3
,小正方体有
?27
个。
平均分成n份:内部棱长为(n-2)
,小正方体有
(n-2)??个。
棱平均分的份数
3份
4份
5份
…
n份
内部棱长
3-2=1
4-2=2
5-2=3
…
n-2
没有涂色的小正方体的总个数
(3-2)?=1
(4-2)?=8
(5-2)?=27
…
(n-2)?
没有涂色的,在大正方体的内部,是边长为n-2的正方体,个数是(n-2)?。
6.
棱长平均分的份数
2份
3份
4份
……
n份
三面涂色的小正方体的个数
8
8
8
……
8
二面涂色的小正方体的总个数
0
12
24
……
12(n-2)
一面涂色的小正方体的总个数
0
6
24
……
6(n-2)?
没有涂色的小正方体的总个数
0
1
8
……
(n-2)?
解析:棱平均分成n份时,三面涂色的有8个,两面涂色的有12?(n-2)?个,一面涂色的有6(n-2)?个,没有涂色的有(n-2)?。
三面涂色的,都是在顶点处的小方块,一个正方体有8个顶点,所以无论n是多少,有三面涂色的都是8个小方块;
两面涂色的,在每条棱上,除去在顶点处的2个,每条棱上有n-2个,总共12条棱,所以是12(n-2)个;
一面涂色的,在每个面上,除去每条棱处的,每个面上有(n-2)?个,总共6个面,所以是6(n-2)?个。
没有涂色的,在大正方体的内部,是边长为n-2的正方体,个数是(n-2)?。
7.(1)8×1=8(个)
(2)(10-2)×12
=96(个)
(3)(10-2)×(10-2)×6=64×6=384(个)
(4)
解法一:10×10×10-(8+96+384)=1000一488=512(个)
解法二:(10-2)×(10-2)×(10-2)=512
答:?(1)三个面涂有红色的有8个;?(2)两个面涂有红色的有96个;?(3)一个面涂有红色的有384个;?(4)六个面都没有涂色的有512个,
第一单元长方体和正方体学霸拓展提优训练二
1.分析:2个正方体拼成1个长方体后,减少了2个正方形面,减少了8条棱的长度。由此可以推出4个正方体拼成1个长方体会减少6个正方形面,也就会减少6×4=24(条)棱的长度。
方法一:
4个小正方体的棱长总和:12×6×4=288(厘米)。
大长方体的棱长总和:(24+6+6)×4-144(厘米)
棱长总和减少了:288-144=144(厘米)
方法二:
6×(6×4)=144(厘米)
答:棱长总和减少了144厘米。
2.解:设它的宽为x厘米,则长为3.x厘米,高为(x+5)厘米。
x+3x+(x+5)=92÷4
x=3.6
3x=3×3.6=10.8
x+5=8.6
答:它的长为10.8厘米,宽为3.6厘米,高为8.6厘米。
3.有2种不同的选法:第1种选①②④,第2种选②③⑤。
4.解:由图可知:?F与A、C、B、E相邻,所以F与D相对;?C与A、F、B、D相邻,所以C与E相对,剩下的A与B相对,所以F的对面是DC的对面是E,A的对面是B
故答案为:F的对面是D,?C的对面是E,?A的对面是B
5.
6.分析:
思路一:画图?理解题意。如图,每个小正方体都有3个面露在外面,而相对的3个面隐藏在里面,也就是说,露在外面的面和隐藏在里面的面的面积是相等的。8个小正方体的表面积之和等于露在外面的面与隐藏在里面的面的面积之和,且露在外面的面的面积和就是大正方体的表面积。因此这些小正方体的表面积之和是大正方体表面积的2倍。
思路二:把一个大正方体切成相等的8个小正方体,需要切3刀,每切l刀,就增加原来大正方体的2个面,切3刀,共增加原来大正方体的6个面。也就是说,增加的面积等于原来大正方体的表面积,即这些小正方体的表面积之和等于大正方体表面积的2倍。
72×2=144(平方厘米)
7.240×10=2400(mL)=2.4(dm?)
2.4÷(2×3)=0.4(dm)
2-1.5=0.5(dm)
0.4dm<0.5dm
答:水不会溢出来。
8.解:
48÷4÷2=6(厘米)
6×6×(6-2)=144(立方厘米)
答:原来长方体的体积是144立方厘米.
思路点拨
根据题意可知,一个长方体,如果高增加2厘米就变成一个正方体,说明长和宽相等且比高长2厘米,因此增加的48平方厘米是4个同样的长方形的面积的和,由此可求出长方体的长,进而求出高,再运用长方体的体积公式将数据代入即可解答.
9.解析
(1)先求出从里面量水槽的长宽高,再根据长方体的体积公式V=abh,代入数据解答;(2)用从外面量的长方体的体积减去水槽的容积,就是所需混凝土的体积,解答即可.
解:
(1)长方体水槽里面的长:15-1×2=13(分米),
宽:8-1×2=6(分米),高5分米;
13×6×5=390(立方分米)
(2)15×8×5-390=210(立方分米)
答:浇筑水槽需要210立方分米的混凝土.
10.解析
由题意可知,将一个长方体平均截成三段,每段长2米,即长方体的高是2×3=6米,表面积增加了16平方米,也就是增加了4个截面的面积,每个截面的面积,即长方体的底面积是16÷4=4平方米,根据长方体的体积公式v=sh,列式解答即可。
解:16÷4×(2×3)=24(立方米)?;
答:原长方体的体积是24立方米.
11.【分析】
我们知道两面涂红色的小正方体都在大正方体的棱上(除去顶点处的两个小正方体),正方体有12条棱,所以每条棱上都有60÷12=5(个)小正方体两面涂色,这说明大正方体的棱长被平均分成了5+2=7份,一面涂色的小正方体均在大正方体每个面的正中间,根据题意如图所示,每个面上都有5×5=25(个)一面涂色的小正方体,大正方体共6个面,所以一面涂色的小正方体个数为25×6=150(个)。
解答:60÷12=5(个)???????5×5×6=150(个)。
答:一面涂红色的小正方体共有150个。
12.【分析】(1)仅有一面涂有红色的小方块在大正方体每个面的正中间,要产生54块,则每个面上应有54÷6=9(块)9=3×3,说明正中间一面涂色的正方形边长为3,则大正方体棱长被平均分成3+2=5等份,那么要切5-1=4(刀)
(2)按题意切割,六个面都没有涂色的小正方体被包裹在大正方体的正中间,要想切出125个,125=5?,这说明正中间的无涂色正方体棱长为5,那么原来大正方体的棱长就被平均分成了5+2=7份,所以这个立方体的各面上应切7-1=6(刀)
??
解答:(1)54÷6=9(块)9=3×3
??3+2-1=4(刀)
?
(2)125=5???5+2-1=6(刀)
答:(1)要想产生54块仅有一面涂有红色的小方块,至少应在各面上切4刀。
(2)要想切出125块大小一样、各面都没有颜色的小立方块,应当在这个立方体的各面上切6刀。
13.(1)切成后,有多少块小正方体木块没有涂上红色?
(4-2)×(5-2)×(6-2)=24(块)
答:有24块小正方体木块没有涂上红色。
切开后,有多少块小正方体木块分别有2面、1面被涂有红色?
2面:[(4-2)+(5-2)+(6-2)]×4=36(块)
1面:[(4-2)×(5-2)+(4-2)×(6-2)+(5-2)×(6-2)]×2=52(块)
答:有36块小正方体木块有2面被涂有红色,有52块小正方体木块有1面被涂有红色。
三面涂色的记作N3:N3=8(个),因为有8个顶点。
两面涂色的记作N2:N2=12(n-2)(个)
一面涂色的记作N1:N1=6(n-2)?(个)
没有一个面涂色的记作N0:N0=(n-2)?(个)。
一、正方体表面涂色的规律及对应考题
(一)正方体表面涂色的规律
⑴当正方体的棱长是a厘米时,这个正方体可以切成棱长是1厘米的小正方体的个数是n×n×n。如果用N表示这样的个数,那么:N=n×n×n(个)
⑵我们把切开的、棱长是1厘米的小正方体分为四种:
⑶上面四种情况的小正方体都是从原来的正方体中切出来的,所以各部分加起来应当等于切成的总个数。也就是:N=n×n×n=N3+N2+N1+N0
(二)正方体表面涂色规律的对应考题(答案见参考答案)
1.(考点)一个表面涂色的正方体,把这个正方体的每条棱平均分成3份、4份、5……再切成同样大的小正方体。那么每种情况中,分割产生的小正方体的总个数各是多少个?请填写下表。
棱长平均分的份数
3份
4份
5份
……
n份
小正方体的总个数
……
2.(考点)三面涂色的小正方体的个数。
观察发现,3面涂色的小正方体都在大正方体(
)的位置上,正方体有
(
)个顶点,即3面涂色的小正方体有(
)个。
3.(考点)二面涂色的小正方体的个数。
观察发现,2面涂色的小正方体都在大正方体(
)的中间。把这个正方体的每条棱平均分成3份、4份、5……再切成同样大的小正方体。那么每种情况中,分割产生的小正方体2面涂色的总个数各是多少个?请填写下表。
棱长平均分的份数
3份
4份
5份
……
n份
每条棱涂色的小正方体的个数
2面涂色的小正方体的总个数
4.(考点)1面涂色的小正方体的个数。
观察发现,1面涂色的小正方体都在大正方体(
)的中间。把这个正方体的每条面平均分成3份、4份、5……再切成同样大的小正方体。那么每种情况中,分割产生的小正方体2面涂色的总个数各是多少个?请填写下表。
棱长平均分的份数
3份
4份
5份
……
n份
每个面涂色的小正方体的个数
一面涂色的小正方体的总个数
5.(考点)6个面都不涂色的小正方体的个数。
观察发现,6个面都不涂色的小正方体在大正方体的(
)。把这个正方体的每条面平均分成3份、4份、5……再切成同样大的小正方体。那么每种情况中,分割产生的小正方体没有涂色的总个数各是多少个?请填写下表。
棱长平均分的份数
3份
4份
5份
……
n份
内部没有涂色的小正方体的个数
没有涂色的小正方体的总个数
(江苏南通期末卷)下图是将涂色的正方体割成小正方体的示意图。
(12分)
①号图表示将正方体的棱长平均分成2份;②号图表示将正方体的棱长平均分成3份;③号图表示将正方体的棱长平均分成4份;那么每种情况中,分割产生的小正方体三面涂色、两面涂色、一面涂色的个数各是多少个?将涂色的大正方体的棱长平均分成n份呢?请填写下表。
棱长平均分的份数
2份
3份
4份
……
n份
三面涂色的小正方体的个数
……
二面涂色的小正方体的总个数
……
一面涂色的小正方体的总个数
……
没有涂色的小正方体的总个数
……
7.(常考题)一个棱长1分米的正方体木块,表面涂满了红色,把它切成棱长1厘米的小正方体。在这些小正方体中:
(1)三个面涂有红色的有多少个??
(2)仅有两面涂有红色的有多少个?????
(3)仅有一个面涂有红色的有多少个??
(4)六个面都没有涂色的有多少个?
第一单元长方体和正方体学霸拓展提优训练二
1.把4个棱长为6厘米的正方体木块拼成1个长方体后,棱长总和减少了多少厘米?
2.一个长方体纸盒的长是宽的3倍,宽比高少5厘米。这个长方体的棱长总和是
92厘米,它的长、宽、高各为多少厘米??(用方程解答)
3.下面的长方形硬纸板各有若干张,从中选三种围成一个长方体,有几种不同的选法?
4.如图是由四个完全一样的正方体拼成的长方体,每个正方体的六个面上分别写有A、B、C、D、E、F六个字母,判断每个正方体相对的面所写的字母。
5.在下图中再添一个小正方形,使它能围成一个正方体。你有多少种不同的方法?
6.亮亮用8个完全相同的小正方体拼成了一个表面积是72平方厘米的大正方体。你能帮亮亮算算原来这8个小正方体的表面积之和是多少吗?
7、下面玻璃缸中已有高1.5dm的水,小红用旁边的水杯装满水往玻璃缸中倒了10次,水会溢出来吗?请通过计算来说明。
8、一个长方体,如果高增加2厘米,就变成了一个正方体(如下图),这时表面积比原来增加48平方厘米。原来长方体的体积是多少立方厘米?
爸爸在院子里用混凝土浇筑了一个无盖的长方体水槽(如图)。?从外面量,水槽长15分米,宽8分米,高5分米,混凝土厚1分米.
(1)这个水槽的容积是多少升?
浇筑这样个水槽需多少混凝土?
10.如图所示,将一个长方体沿长平均截成3段,每段2米,表面积增加了16平方米,原长方体的体积是多少立方米?
11.(常考题)一个涂满红色的正方体,每面等距离切若干刀后,得到一些同样大的小正方体,其中两面涂红的共计60块,那么一面涂红的小正方体有多少块
12.(拓展延伸)一个涂满红色的正方体,每面等距离切若干刀后会得到一些同样大的小正方体,那么:
(1)要想产生54块仅有一面涂有红色的小方块,至少应在各面上切______刀。
(2)要想切出125块大小一样、各面都没有颜色的小正方体,应当在这个大正方体的各面上切______刀(各面切的刀数一样)。
13.[拓展延伸]把一个长为5cm、宽4cm、高6em的长方体木块表面全部涂上红色,然后切成棱长为1厘米的小正方体木块。
(1)切成后,有多少块小正方体木块没有涂上红色?
(2)切开后,有多少块小正方体木块分别有2面、1面被涂有红色?
参考答案与难题详解见下一页
答案就是咱无声的老师
正方体表面涂色的规律及对应考题答案
1.平均切成3份:3×3×3=27(个)
平均切成4份:4×4×4=64(个)
平均切成5份:5×5×5=125(个)
平均切成n份:n?
个
棱平均分的份数
3份
4份
5份
……
n份
小正方体的总个数
3?=27
4?=64
5?=125
……
n?
顶点
8
8
有三面涂色的,都是在顶点处的小方块,一个正方体有8个顶点,所以无论n是多少,有三面涂色的都是8个小方块
观察发现,2面涂色的小正方体都在大正方体(棱
)的中间。
平均分成3份,每条棱上有
1
个,12条棱上共有
12?个。
平均分成4份,每条棱上有
2
个,12条棱上共有
24?
个。
平均分成5份,每条棱上有
3
个,12条棱上共有
36
个。
平均分成n份,每条棱上有(n-2)个,12条棱上共有12(n-2)?个。
棱平均分的份数
3份
4份
5份
……
n份
每条棱涂色的小正方体的个数
3-2=1
4-2=2
5-2=3
……
n-2
2面涂色的小正方体的总个数
1×12=12
2×12=24
3×12=36
……
(n-2)×12
两面涂色的,在每条棱上,除去在顶点处的2个,每条棱上有n-2个,总共12条棱,所以是12(n-2)个;
4.观察发现,1面涂色的小正方体都在大正方体(面)的中间。
平均分成3份,每面有
1
个,6面共有
6
个。
平均分成4份,每面有
4
个,6面共有
24
个。
平均分成5份,每面有
9
个,6面共有
54
个。
平均分成n份,每面有
?(n-2)?
个,6面共有
6(n-2)?个。
棱平均分的份数
3份
4份
5份
…
n份
每个面涂色的小正方体的个数
(3-2)?=1
(4-2)?=4
(5-2)?=9
…
(n-2)?
2面涂色的小正方体的总个数
6×(3-2)?=6
6×(4-2)?=24
6×(5-3)?=54
…
6(n-2)?
一面涂色的,在每个面上,除去每条棱处的,每个面上有(n-2)?个,总共6个面,所以是6(n-2)?个。
观察发现,6个面都不涂色的小正方体在大正方体的(内部)。
平均分成3份:内部棱长为1
,小正方体有
?1
个。
平均分成4份:内部棱长为2
,小正方体有
?8
?个。
平均分成5份:内部棱长为3
,小正方体有
?27
个。
平均分成n份:内部棱长为(n-2)
,小正方体有
(n-2)??个。
棱平均分的份数
3份
4份
5份
…
n份
内部棱长
3-2=1
4-2=2
5-2=3
…
n-2
没有涂色的小正方体的总个数
(3-2)?=1
(4-2)?=8
(5-2)?=27
…
(n-2)?
没有涂色的,在大正方体的内部,是边长为n-2的正方体,个数是(n-2)?。
6.
棱长平均分的份数
2份
3份
4份
……
n份
三面涂色的小正方体的个数
8
8
8
……
8
二面涂色的小正方体的总个数
0
12
24
……
12(n-2)
一面涂色的小正方体的总个数
0
6
24
……
6(n-2)?
没有涂色的小正方体的总个数
0
1
8
……
(n-2)?
解析:棱平均分成n份时,三面涂色的有8个,两面涂色的有12?(n-2)?个,一面涂色的有6(n-2)?个,没有涂色的有(n-2)?。
三面涂色的,都是在顶点处的小方块,一个正方体有8个顶点,所以无论n是多少,有三面涂色的都是8个小方块;
两面涂色的,在每条棱上,除去在顶点处的2个,每条棱上有n-2个,总共12条棱,所以是12(n-2)个;
一面涂色的,在每个面上,除去每条棱处的,每个面上有(n-2)?个,总共6个面,所以是6(n-2)?个。
没有涂色的,在大正方体的内部,是边长为n-2的正方体,个数是(n-2)?。
7.(1)8×1=8(个)
(2)(10-2)×12
=96(个)
(3)(10-2)×(10-2)×6=64×6=384(个)
(4)
解法一:10×10×10-(8+96+384)=1000一488=512(个)
解法二:(10-2)×(10-2)×(10-2)=512
答:?(1)三个面涂有红色的有8个;?(2)两个面涂有红色的有96个;?(3)一个面涂有红色的有384个;?(4)六个面都没有涂色的有512个,
第一单元长方体和正方体学霸拓展提优训练二
1.分析:2个正方体拼成1个长方体后,减少了2个正方形面,减少了8条棱的长度。由此可以推出4个正方体拼成1个长方体会减少6个正方形面,也就会减少6×4=24(条)棱的长度。
方法一:
4个小正方体的棱长总和:12×6×4=288(厘米)。
大长方体的棱长总和:(24+6+6)×4-144(厘米)
棱长总和减少了:288-144=144(厘米)
方法二:
6×(6×4)=144(厘米)
答:棱长总和减少了144厘米。
2.解:设它的宽为x厘米,则长为3.x厘米,高为(x+5)厘米。
x+3x+(x+5)=92÷4
x=3.6
3x=3×3.6=10.8
x+5=8.6
答:它的长为10.8厘米,宽为3.6厘米,高为8.6厘米。
3.有2种不同的选法:第1种选①②④,第2种选②③⑤。
4.解:由图可知:?F与A、C、B、E相邻,所以F与D相对;?C与A、F、B、D相邻,所以C与E相对,剩下的A与B相对,所以F的对面是DC的对面是E,A的对面是B
故答案为:F的对面是D,?C的对面是E,?A的对面是B
5.
6.分析:
思路一:画图?理解题意。如图,每个小正方体都有3个面露在外面,而相对的3个面隐藏在里面,也就是说,露在外面的面和隐藏在里面的面的面积是相等的。8个小正方体的表面积之和等于露在外面的面与隐藏在里面的面的面积之和,且露在外面的面的面积和就是大正方体的表面积。因此这些小正方体的表面积之和是大正方体表面积的2倍。
思路二:把一个大正方体切成相等的8个小正方体,需要切3刀,每切l刀,就增加原来大正方体的2个面,切3刀,共增加原来大正方体的6个面。也就是说,增加的面积等于原来大正方体的表面积,即这些小正方体的表面积之和等于大正方体表面积的2倍。
72×2=144(平方厘米)
7.240×10=2400(mL)=2.4(dm?)
2.4÷(2×3)=0.4(dm)
2-1.5=0.5(dm)
0.4dm<0.5dm
答:水不会溢出来。
8.解:
48÷4÷2=6(厘米)
6×6×(6-2)=144(立方厘米)
答:原来长方体的体积是144立方厘米.
思路点拨
根据题意可知,一个长方体,如果高增加2厘米就变成一个正方体,说明长和宽相等且比高长2厘米,因此增加的48平方厘米是4个同样的长方形的面积的和,由此可求出长方体的长,进而求出高,再运用长方体的体积公式将数据代入即可解答.
9.解析
(1)先求出从里面量水槽的长宽高,再根据长方体的体积公式V=abh,代入数据解答;(2)用从外面量的长方体的体积减去水槽的容积,就是所需混凝土的体积,解答即可.
解:
(1)长方体水槽里面的长:15-1×2=13(分米),
宽:8-1×2=6(分米),高5分米;
13×6×5=390(立方分米)
(2)15×8×5-390=210(立方分米)
答:浇筑水槽需要210立方分米的混凝土.
10.解析
由题意可知,将一个长方体平均截成三段,每段长2米,即长方体的高是2×3=6米,表面积增加了16平方米,也就是增加了4个截面的面积,每个截面的面积,即长方体的底面积是16÷4=4平方米,根据长方体的体积公式v=sh,列式解答即可。
解:16÷4×(2×3)=24(立方米)?;
答:原长方体的体积是24立方米.
11.【分析】
我们知道两面涂红色的小正方体都在大正方体的棱上(除去顶点处的两个小正方体),正方体有12条棱,所以每条棱上都有60÷12=5(个)小正方体两面涂色,这说明大正方体的棱长被平均分成了5+2=7份,一面涂色的小正方体均在大正方体每个面的正中间,根据题意如图所示,每个面上都有5×5=25(个)一面涂色的小正方体,大正方体共6个面,所以一面涂色的小正方体个数为25×6=150(个)。
解答:60÷12=5(个)???????5×5×6=150(个)。
答:一面涂红色的小正方体共有150个。
12.【分析】(1)仅有一面涂有红色的小方块在大正方体每个面的正中间,要产生54块,则每个面上应有54÷6=9(块)9=3×3,说明正中间一面涂色的正方形边长为3,则大正方体棱长被平均分成3+2=5等份,那么要切5-1=4(刀)
(2)按题意切割,六个面都没有涂色的小正方体被包裹在大正方体的正中间,要想切出125个,125=5?,这说明正中间的无涂色正方体棱长为5,那么原来大正方体的棱长就被平均分成了5+2=7份,所以这个立方体的各面上应切7-1=6(刀)
??
解答:(1)54÷6=9(块)9=3×3
??3+2-1=4(刀)
?
(2)125=5???5+2-1=6(刀)
答:(1)要想产生54块仅有一面涂有红色的小方块,至少应在各面上切4刀。
(2)要想切出125块大小一样、各面都没有颜色的小立方块,应当在这个立方体的各面上切6刀。
13.(1)切成后,有多少块小正方体木块没有涂上红色?
(4-2)×(5-2)×(6-2)=24(块)
答:有24块小正方体木块没有涂上红色。
切开后,有多少块小正方体木块分别有2面、1面被涂有红色?
2面:[(4-2)+(5-2)+(6-2)]×4=36(块)
1面:[(4-2)×(5-2)+(4-2)×(6-2)+(5-2)×(6-2)]×2=52(块)
答:有36块小正方体木块有2面被涂有红色,有52块小正方体木块有1面被涂有红色。
三面涂色的记作N3:N3=8(个),因为有8个顶点。
两面涂色的记作N2:N2=12(n-2)(个)
一面涂色的记作N1:N1=6(n-2)?(个)
没有一个面涂色的记作N0:N0=(n-2)?(个)。
