3.1.1函数的概念 课件(共25张PPT)
文档属性
| 名称 | 3.1.1函数的概念 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 14:57:47 | ||
图片预览







文档简介
(共25张PPT)
人教A版(2019)
必修第一册
3.1
函数的概念及其表示
3.1.1 函数的概念
1.建立完整的函数概念,体会集合语言和对应关系在刻画函数概念中的作用.
2.了解构成函数的要素,能求简单函数的定义域.
3.会正确使用函数、区间符号.
1.函数的有关概念
2.同一个函数
如果两个函数的⑧ 定义域????相同,并且⑨ 对应关系????完全一致,我们就称这两
个函数是同一个函数.
函数的定义
一般地,设A,B是① 非空的实数集????,如果对于集合A中的② 任意????一个数x,按照某种确定的对应关系f,在集合B中都有③ 唯一确定????的数y和它对应,那么就称④????f:A→B????为从集合A到集合B的一个函数
函数的记法
⑤????y=f(x)????,x∈A
定义域
x叫做自变量,x的⑥ 取值范围A????叫做函数的
定义域
值域
函数值的集合⑦ {f(x)|x∈A}????叫做函数的值域
函数的有关概念
1.一般区间的表示
设a,b是两个实数,而且a定义
名称
符号
数轴表示
{x|a≤x≤b}
闭区间
⑩ [a,b]????
?
{x|a开区间
? (a,b)????
?
{x|a≤x半开半闭区间
[a,b)
?
{x|a半开半闭区间
(a,b]
?
区间的概念及表示
定义
区间
数轴表示
{x|x≥a}
[a,+∞)
?
{x|x>a}
(a,+∞)
?
{x|x≤b}
(-∞,b]
?
{x|x(-∞,b)
?
2.特殊区间的表示
某物体从高度为19.6
m的空中自由下落,物体下落的距离s(m)与所用时间t(s)的平
方成正比,这个规律用数学式子可以描述为s=?gt2,其中g取9.8
m/s2.判断第1~3题是
否正确.
1.函数的定义域为[0,2].?( √ )
2.函数的值域为[0,+∞).?(????? )
3.当t=1时,物体下落的距离是4.9
m.?( √ )
4.函数的定义域和值域一定是无限集合.?(????? )
提示:函数的定义域和值域也可能是有限集,如f(x)=1.
判断正误,正确的画“√”
,错误的画“
?”
.
5.根据函数的定义,定义域中的任何一个x可以对应着值域中不同的y.?(????? )
提示:根据函数的定义,对于定义域中的任何一个x,在值域中都有唯一确定的y与之
对应.
6.在函数的定义中,集合B是函数的值域.?(????? )
提示:在函数的定义中,函数的值域是{f(x)|x∈A},它是集合B的子集.
已知函数解析式求定义域
(1)如果函数解析式是整式,那么在没有指明它的定义域的情况下,函数的定义域是
实数集R.
(2)如果函数解析式仅含分式,那么函数的定义域是使分母不等于零的实数的集合.
(3)如果函数解析式仅含偶次根式,那么函数的定义域是使根号内的式子大于或等
于零的实数的集合.
(4)如果函数解析式是由几个部分的数学式子构成的,那么函数定义域是使各部分
式子都有意义的实数的集合(即求各部分定义域的交集).
(5)由实际背景确定的函数,其定义域要受实际问题的制约.
如何求函数的定义域
??
求下列函数的定义域:
(1)f(x)=?+?;
(2)f(x)=?;
(3)y=?.
思路点拨
求函数的定义域就是求使函数解析式有意义的自变量的取值范围,可考虑列不等
式或不等式组.
解析????(1)要使函数有意义,只需?解得?≤x≤?.则函数的定义域为?x??≤
x≤??.
(2)要使函数有意义,只需?解得-2≤x≤2,且x≠1.则函数的定义域为{x|-2≤x
≤2,且x≠1}.
(3)要使函数有意义,只需?解得x>-2,且x≠-1.则函数的定义域为{x|x>-2,且x
≠-1}.
?求抽象函数的定义域
求抽象函数的定义域,要明确以下几点:
(1)函数f(x)的定义域是指x的取值范围.
(2)函数f(φ(x))的定义域是指x的取值范围,而不是φ(x)的取值范围.
(3)f(t),
f(φ(x)),
f(h(x))三个函数中的t,φ(x),h(x)在对应关系f下的取值范围相同.
(4)已知f(x)的定义域为A,求f(φ(x))的定义域,实质是已知φ(x)的取值范围为A,求x的
取值范围.
(5)已知f(φ(x))的定义域为B,求f(x)的定义域,实质是已知x的取值范围为B,求φ(x)的
取值范围,此范围就是f(x)的定义域.
(6)已知f(φ(x))的定义域为C,求f(g(x))的定义域,实质是已知φ(x)中的x的取值范围为
C,求出φ(x)的取值范围D,再令g(x)的取值范围为D,求出x的取值范围,此范围就是f(g
(x))的定义域.
??
1)已知函数f(x)的定义域为[1,3],求函数f(2x+1)的定义域;
(2)已知函数f(2x+1)的定义域为[1,3],求函数f(x)的定义域;
(3)已知函数f(2x+1)的定义域为[1,3],求函数f(3x)的定义域;
(4)已知函数f(x)的定义域为[0,1],求函数g(x)=f(x+m)+f(x-m)(m>0)的定义域.
思路点拨
根据抽象函数定义域的实质列出不等式(组)求解,对于含参数的抽象函数要注意分
类讨论.
解析????(1)由题意知,函数f(2x+1)中2x+1的范围与函数f(x)中x的范围相同,
∵x∈[1,3],∴2x+1∈[1,3],即x∈[0,1],
∴函数f(2x+1)的定义域为[0,1].
(2)∵x∈[1,3],∴2x+1∈[3,7],
∴函数f(x)的定义域为[3,7].
(3)∵x∈[1,3],
∴2x+1∈[3,7],
∴3x∈[3,7],即x∈?,
∴函数f(3x)的定义域为?.
(4)依题意有
???
∵m>0,∴-m<0,1-m<1+m,但m与1-m的大小不确定,∴对m与1-m的大小分类讨论.
①若m=1-m,即m=?,
则x=m=?;
②若m<1-m,即m则m≤x≤1-m;
③若m>1-m,即m>?,
则x∈?,与题意不符.
综上,01.求函数值的方法
(1)已知函数f(x)的解析式时,只需用常数a替换解析式中的x并进行计算,即得f(a)的
值.
(2)已知函数f(x)与g(x),求f(g(a))的值,应遵循由内到外的原则.
注意:用来替换解析式中x的常数a必须是函数定义域内的值,否则求值无意义.
2.已知函数值求自变量的对应值的方法
(1)已知函数f(x)的解析式时,列方程f(x)=a,解出其中的x,即可得到函数值为a时x的
值.
(2)已知函数f(x)与g(x),求f(g(x))=a中的x的值,可以由内到外,也可由外到内进行求
解.
??
如何解决函数求值问题
已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
思路点拨
本题是函数求值的问题,(1)(2)分别将自变量的值代入解析式中求解即可,(3)可以由
外到内,也可以由内到外求解.
解析????(1)f(2)=11+2=13.
g(2)=22+2=6.
(2)g(3)=32+2=11,
∴f(g(3))=f(11)=11+11=22.
(3)解法一:∵f(g(x))=14,
∴11+g(x)=14,
解得g(x)=3,
∴x2+2=3,解得x=±1.
解法二:∵f(g(x))=f(x2+2)
=11+x2+2=13+x2,
∴13+x2=14,∴x2=1,解得x=±1.
张先生的家离单位15
km,张先生从家出发开车以50
km/h的速度到单位去上
班,设张先生开车行驶的路程为y(km),行驶的时间为x(h).
问题
1.张先生开车行驶的路程y(km)与行驶的时间x(h)之间的函数关系式是什么?
提示:行驶的路程y(km)与行驶的时间x(h)的函数关系式是y=50x.
2.问题1中函数的定义域是什么?
提示:函数的定义域是{x|0≤x≤0.3}.
3.这个函数与我们熟悉的一次函数y=50x是不是同一个函数?
提示:不是同一个函数,两函数的定义域不同.
如何判断两个函数是不是同一个函数
?判断两个函数是不是同一个函数时应注意的三点
(1)定义域、对应关系两者中只要有一个不相同就不是同一个函数,即使定义域与
值域都相同,也不一定是同一个函数.
(2)函数是两个数集之间的对应关系,所以用什么字母表示自变量、因变量是没有
限制的.
(3)要化简解析式,必须先求定义域,否则可能导致定义域发生变化.
??
下列各组函数:
①f(x)=?,g(x)=x-1;
②f(x)=?,g(x)=?;
③f(x)=x+1,g(x)=x+x0;
④f(x)=x0,g(x)=?;
⑤f(x)=(x-1)2,g(t)=t2-2t+1.
其中表示同一个函数的是 ????(填上所有正确的序号).
思路点拨
先求各组中两个函数的定义域,若定义域不同,则它们不是同一个函数;若定义域相
同,再化简函数解析式,判断对应关系是否相同.
解析????①f(x)的定义域为{x|x∈R,且x≠0},g(x)的定义域为R,
f(x)与g(x)的定义域不
同,不是同一个函数;②f(x)与g(x)的定义域都是{x|x>0},f(x)=?,g(x)=?,它们的对
应关系不同,不是同一个函数;③f(x)的定义域为R,g(x)的定义域为{x|x∈R,且x≠0},f
(x)与g(x)的定义域不同,不是同一个函数;④f(x)与g(x)的定义域、对应关系皆相同,
故是同一个函数;⑤虽然表示自变量的字母不同,但f(x)与g(t)的定义域相同,对应关
系相同,故是同一个函数.
答案 ④⑤
?
定义域、对应关系都相同,两函数是同一个函数,与表示自变量的字母是否相同无
关.
?
判断下列函数是不是同一个函数:
(1)f(x)=?,g(x)=?
(2)f(x)=??,g(x)=?;
(3)f(x)=2,g(x)=?.
思路点拨
判断函数的定义域和对应关系是否相同.
解析????(1)f(x)的定义域中不含有元素0,而g(x)的定义域为R,定义域不相同,所以二
者不是同一个函数.
(2)f(x)的定义域为[0,+∞),而g(x)的定义域为(-∞,-1]∪[0,+∞),定义域不相同,所以二
者不是同一个函数.
(3)f(x)与g(x)的定义域都是实数集R,将g(x)的解析式化简后知两函数的对应关系相
同,因此二者是同一个函数.
https://www.21cnjy.com/help/help_extract.php
人教A版(2019)
必修第一册
3.1
函数的概念及其表示
3.1.1 函数的概念
1.建立完整的函数概念,体会集合语言和对应关系在刻画函数概念中的作用.
2.了解构成函数的要素,能求简单函数的定义域.
3.会正确使用函数、区间符号.
1.函数的有关概念
2.同一个函数
如果两个函数的⑧ 定义域????相同,并且⑨ 对应关系????完全一致,我们就称这两
个函数是同一个函数.
函数的定义
一般地,设A,B是① 非空的实数集????,如果对于集合A中的② 任意????一个数x,按照某种确定的对应关系f,在集合B中都有③ 唯一确定????的数y和它对应,那么就称④????f:A→B????为从集合A到集合B的一个函数
函数的记法
⑤????y=f(x)????,x∈A
定义域
x叫做自变量,x的⑥ 取值范围A????叫做函数的
定义域
值域
函数值的集合⑦ {f(x)|x∈A}????叫做函数的值域
函数的有关概念
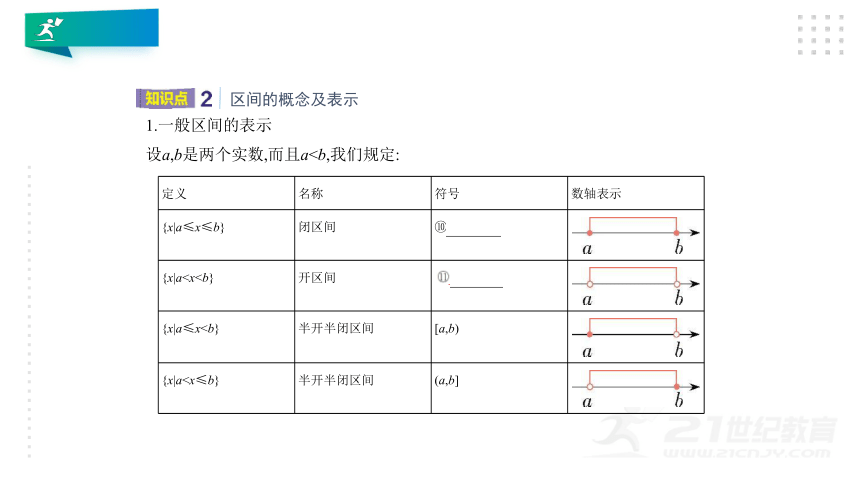
1.一般区间的表示
设a,b是两个实数,而且a
名称
符号
数轴表示
{x|a≤x≤b}
闭区间
⑩ [a,b]????
?
{x|a
? (a,b)????
?
{x|a≤x
[a,b)
?
{x|a
(a,b]
?
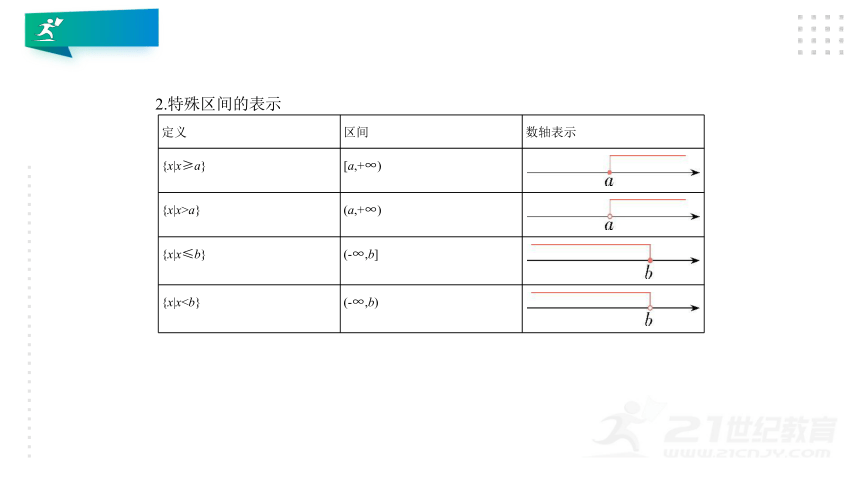
区间的概念及表示
定义
区间
数轴表示
{x|x≥a}
[a,+∞)
?
{x|x>a}
(a,+∞)
?
{x|x≤b}
(-∞,b]
?
{x|x
?
2.特殊区间的表示
某物体从高度为19.6
m的空中自由下落,物体下落的距离s(m)与所用时间t(s)的平
方成正比,这个规律用数学式子可以描述为s=?gt2,其中g取9.8
m/s2.判断第1~3题是
否正确.
1.函数的定义域为[0,2].?( √ )
2.函数的值域为[0,+∞).?(????? )
3.当t=1时,物体下落的距离是4.9
m.?( √ )
4.函数的定义域和值域一定是无限集合.?(????? )
提示:函数的定义域和值域也可能是有限集,如f(x)=1.
判断正误,正确的画“√”
,错误的画“
?”
.
5.根据函数的定义,定义域中的任何一个x可以对应着值域中不同的y.?(????? )
提示:根据函数的定义,对于定义域中的任何一个x,在值域中都有唯一确定的y与之
对应.
6.在函数的定义中,集合B是函数的值域.?(????? )
提示:在函数的定义中,函数的值域是{f(x)|x∈A},它是集合B的子集.
已知函数解析式求定义域
(1)如果函数解析式是整式,那么在没有指明它的定义域的情况下,函数的定义域是
实数集R.
(2)如果函数解析式仅含分式,那么函数的定义域是使分母不等于零的实数的集合.
(3)如果函数解析式仅含偶次根式,那么函数的定义域是使根号内的式子大于或等
于零的实数的集合.
(4)如果函数解析式是由几个部分的数学式子构成的,那么函数定义域是使各部分
式子都有意义的实数的集合(即求各部分定义域的交集).
(5)由实际背景确定的函数,其定义域要受实际问题的制约.
如何求函数的定义域
??
求下列函数的定义域:
(1)f(x)=?+?;
(2)f(x)=?;
(3)y=?.
思路点拨
求函数的定义域就是求使函数解析式有意义的自变量的取值范围,可考虑列不等
式或不等式组.
解析????(1)要使函数有意义,只需?解得?≤x≤?.则函数的定义域为?x??≤
x≤??.
(2)要使函数有意义,只需?解得-2≤x≤2,且x≠1.则函数的定义域为{x|-2≤x
≤2,且x≠1}.
(3)要使函数有意义,只需?解得x>-2,且x≠-1.则函数的定义域为{x|x>-2,且x
≠-1}.
?求抽象函数的定义域
求抽象函数的定义域,要明确以下几点:
(1)函数f(x)的定义域是指x的取值范围.
(2)函数f(φ(x))的定义域是指x的取值范围,而不是φ(x)的取值范围.
(3)f(t),
f(φ(x)),
f(h(x))三个函数中的t,φ(x),h(x)在对应关系f下的取值范围相同.
(4)已知f(x)的定义域为A,求f(φ(x))的定义域,实质是已知φ(x)的取值范围为A,求x的
取值范围.
(5)已知f(φ(x))的定义域为B,求f(x)的定义域,实质是已知x的取值范围为B,求φ(x)的
取值范围,此范围就是f(x)的定义域.
(6)已知f(φ(x))的定义域为C,求f(g(x))的定义域,实质是已知φ(x)中的x的取值范围为
C,求出φ(x)的取值范围D,再令g(x)的取值范围为D,求出x的取值范围,此范围就是f(g
(x))的定义域.
??
1)已知函数f(x)的定义域为[1,3],求函数f(2x+1)的定义域;
(2)已知函数f(2x+1)的定义域为[1,3],求函数f(x)的定义域;
(3)已知函数f(2x+1)的定义域为[1,3],求函数f(3x)的定义域;
(4)已知函数f(x)的定义域为[0,1],求函数g(x)=f(x+m)+f(x-m)(m>0)的定义域.
思路点拨
根据抽象函数定义域的实质列出不等式(组)求解,对于含参数的抽象函数要注意分
类讨论.
解析????(1)由题意知,函数f(2x+1)中2x+1的范围与函数f(x)中x的范围相同,
∵x∈[1,3],∴2x+1∈[1,3],即x∈[0,1],
∴函数f(2x+1)的定义域为[0,1].
(2)∵x∈[1,3],∴2x+1∈[3,7],
∴函数f(x)的定义域为[3,7].
(3)∵x∈[1,3],
∴2x+1∈[3,7],
∴3x∈[3,7],即x∈?,
∴函数f(3x)的定义域为?.
(4)依题意有
???
∵m>0,∴-m<0,1-m<1+m,但m与1-m的大小不确定,∴对m与1-m的大小分类讨论.
①若m=1-m,即m=?,
则x=m=?;
②若m<1-m,即m则m≤x≤1-m;
③若m>1-m,即m>?,
则x∈?,与题意不符.
综上,0
(1)已知函数f(x)的解析式时,只需用常数a替换解析式中的x并进行计算,即得f(a)的
值.
(2)已知函数f(x)与g(x),求f(g(a))的值,应遵循由内到外的原则.
注意:用来替换解析式中x的常数a必须是函数定义域内的值,否则求值无意义.
2.已知函数值求自变量的对应值的方法
(1)已知函数f(x)的解析式时,列方程f(x)=a,解出其中的x,即可得到函数值为a时x的
值.
(2)已知函数f(x)与g(x),求f(g(x))=a中的x的值,可以由内到外,也可由外到内进行求
解.
??
如何解决函数求值问题
已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
思路点拨
本题是函数求值的问题,(1)(2)分别将自变量的值代入解析式中求解即可,(3)可以由
外到内,也可以由内到外求解.
解析????(1)f(2)=11+2=13.
g(2)=22+2=6.
(2)g(3)=32+2=11,
∴f(g(3))=f(11)=11+11=22.
(3)解法一:∵f(g(x))=14,
∴11+g(x)=14,
解得g(x)=3,
∴x2+2=3,解得x=±1.
解法二:∵f(g(x))=f(x2+2)
=11+x2+2=13+x2,
∴13+x2=14,∴x2=1,解得x=±1.
张先生的家离单位15
km,张先生从家出发开车以50
km/h的速度到单位去上
班,设张先生开车行驶的路程为y(km),行驶的时间为x(h).
问题
1.张先生开车行驶的路程y(km)与行驶的时间x(h)之间的函数关系式是什么?
提示:行驶的路程y(km)与行驶的时间x(h)的函数关系式是y=50x.
2.问题1中函数的定义域是什么?
提示:函数的定义域是{x|0≤x≤0.3}.
3.这个函数与我们熟悉的一次函数y=50x是不是同一个函数?
提示:不是同一个函数,两函数的定义域不同.
如何判断两个函数是不是同一个函数
?判断两个函数是不是同一个函数时应注意的三点
(1)定义域、对应关系两者中只要有一个不相同就不是同一个函数,即使定义域与
值域都相同,也不一定是同一个函数.
(2)函数是两个数集之间的对应关系,所以用什么字母表示自变量、因变量是没有
限制的.
(3)要化简解析式,必须先求定义域,否则可能导致定义域发生变化.
??
下列各组函数:
①f(x)=?,g(x)=x-1;
②f(x)=?,g(x)=?;
③f(x)=x+1,g(x)=x+x0;
④f(x)=x0,g(x)=?;
⑤f(x)=(x-1)2,g(t)=t2-2t+1.
其中表示同一个函数的是 ????(填上所有正确的序号).
思路点拨
先求各组中两个函数的定义域,若定义域不同,则它们不是同一个函数;若定义域相
同,再化简函数解析式,判断对应关系是否相同.
解析????①f(x)的定义域为{x|x∈R,且x≠0},g(x)的定义域为R,
f(x)与g(x)的定义域不
同,不是同一个函数;②f(x)与g(x)的定义域都是{x|x>0},f(x)=?,g(x)=?,它们的对
应关系不同,不是同一个函数;③f(x)的定义域为R,g(x)的定义域为{x|x∈R,且x≠0},f
(x)与g(x)的定义域不同,不是同一个函数;④f(x)与g(x)的定义域、对应关系皆相同,
故是同一个函数;⑤虽然表示自变量的字母不同,但f(x)与g(t)的定义域相同,对应关
系相同,故是同一个函数.
答案 ④⑤
?
定义域、对应关系都相同,两函数是同一个函数,与表示自变量的字母是否相同无
关.
?
判断下列函数是不是同一个函数:
(1)f(x)=?,g(x)=?
(2)f(x)=??,g(x)=?;
(3)f(x)=2,g(x)=?.
思路点拨
判断函数的定义域和对应关系是否相同.
解析????(1)f(x)的定义域中不含有元素0,而g(x)的定义域为R,定义域不相同,所以二
者不是同一个函数.
(2)f(x)的定义域为[0,+∞),而g(x)的定义域为(-∞,-1]∪[0,+∞),定义域不相同,所以二
者不是同一个函数.
(3)f(x)与g(x)的定义域都是实数集R,将g(x)的解析式化简后知两函数的对应关系相
同,因此二者是同一个函数.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
