【人教九上数学学霸听课笔记】21.1 一元二次方程 课件(共29张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】21.1 一元二次方程 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 22:30:26 | ||
图片预览








文档简介
(共28张PPT)
21.1 一元二次方程
第二十一章
一元二次方程
21.1 一元二次方程
预学浅梳理
探究与应用
随堂小检测
第二十一章 一元二次方程
1.观察方程2x2=1,x2-2x=0,4y2=y+1,它们等号的两边都
是________式,方程中都只含有________个未知数,并且未
知数的最高次数是________,像这样的方程,叫做一元二次
方程.
整
一
2
2.一元二次方程的一般形式是ax2+bx+c=0(a≠0),其中
________是二次项,________是二次项系数;________是一
次项,________是一次项系数;________是常数项.
3.使方程左右两边________的未知数的值就是这个一元二
次方程的解,一元二次方程的解也叫做一元二次方程的
________.
ax2
a
bx
b
c
相等
根
目标一 理解一元二次方程的概念
问题1
如图21-1-1,有一块矩形铁皮,长100
cm,宽50
cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3600
cm2,那么铁皮各角应切去多大的正方形?(要求只列出方程)
图21-1-1
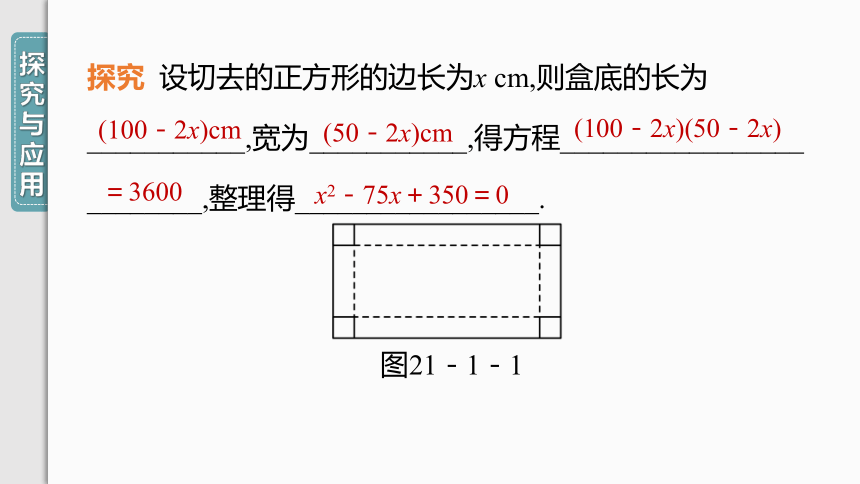
探究
设切去的正方形的边长为x
cm,则盒底的长为
___________,宽为___________,得方程_________________
________,整理得_________________.
(100-2x)cm
(50-2x)cm
(100-2x)(50-2x)
=3600
x2-75x+350=0
图21-1-1
问题2
要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?(要求只列出方程)
探究
全部比赛的场数为_________.
设应邀请x个队参赛,每个队要与其他(x-1)个队各赛1场,所以全部比赛共_________场.列方程____________,化简整理得___________.
7×4=28
x2-x=56
思考
观察问题1与问题2中得出的方程及方程x2+2x-4=0,5y2+y=0,2y2=18,你发现它们的共同点是什么?
解:共同点:方程中等号的两边都是整式,方程中只含有一个未知数,并且未知数的最高次数是2.
定义
等号两边都是整式,只含有________个未知数,并且未知数的____________是2的方程,叫做一元二次方程.
一
最高次数
C
归纳
判定一元二次方程的关键要素
方程中
(1)等号两边都是________;
(2)____________未知数;
(3)未知数的最高次数是________.
整式
只含有一个
2
目标二 掌握一元二次方程的一般形式,正确认识二次项
系数、一次项系数及常数项
问题3
将前面思考中的五个方程的各项都移到等号的左边,并按所含未知数的降幂排列,等号右边变为0,它们是否都符合ax2+bx+c=0(a≠0)的形式?把它们化成ax2+bx+c=0形式后的二次项系数、一次项系数、常数项分别是什么?
解:方程x2-75x+350=0符合ax2+bx+c=0(a≠0)的形式,它的二次项系数是1,一次项系数是-75,常数项是350;方程x2-x=56整理,得x2-x-56=0,符合ax2+bx+c=0(a≠0)的形式,方程x2-x-56=0的二次项系数是1,一次项系数是-1,常数项是-56;方程x2+2x-4=0符合ax2+bx+c=0(a≠0)的形式,它的二次项系数是1,一次项系数是2,常数项是-4;5y2+y=0符合ax2+bx+c=0(a≠0)的形式,它的二次项系数是5,一次项系数是1,常数项是0;2y2=18化成一般形式是2y2-18=0,符合ax2+bx+c=0(a≠0)的形式,它的二次项系数是2,一次项系数是0,常数项是-18.
总结
一元二次方程的一般形式
ax2+bx+c=0(a≠0)
二次项
系数
一次项
系数
常数项
例2
[教材P3例题]将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项.
解:去括号,得3x2-3x=5x+10.
移项,合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
其中二次项系数为3,一次项系数为-8,常数项为-10.
变式1
方程x2-2(3x-2)+(x+1)=0的一般形式是( )
A.x2-5x+5=0
B.x2+5x+5=0
C.x2+5x-5=0
D.x2+5=0
A
变式2
一个关于x的一元二次方程,它的二次项系数为3,一次项系数为2,常数项为-6,则这个一元二次方程是________________.
3x2+2x-6=0
目标三 理解一元二次方程根的意义
例3
下列哪些数是方程x2+2x-8=0的根?
-4,-3,0,2,4.
解:将x=-4代入方程x2+2x-8=0,左边=(-4)2+(-4)×2-8=0,即左边=右边,故-4是方程x2+2x-8=0的根.
同理可得,-3,0,4都不是方程x2+2x-8=0的根.
将x=2代入方程x2+2x-8=0,左边=22+2×2-8=0,即左边=右边,故2是方程x2+2x-8=0的根.
拓展
若关于x的一元二次方程(a-1)x2+x+|a|-1=0的一个根是0,则实数a的值是________.
[解析]
依题意,得|a|-1=0且a-1≠0,解得a=-1.
-1
拓展
已知关于x的方程x2+bx+a=0的一个根是x=-a
(a≠0),则a-b的值为(
)
A.-1
B.0
C.1
D.2
A
A
2.一元二次方程2y2-7=3y的二次项系数、一次项系数、常数项分别是( )
A.2,-3,-7
B.-2,-3,-7
C.2,-7,3
D.-2,-3,7
[解析]
2y2-7=3y,整理,得2y2-3y-7=0,
所以一元二次方程2y2-7=3y的二次项系数、一次项系数、常数项分别是2,-3,-7.
A
3.已知关于x的方程x2-mx+1=0的一个根为1,那么m的值是________.
[解析]
将x=1代入方程x2-mx+1=0,得12-m+1=0,
即2-m=0,
解得m=2.
2
图21-1-2
解:(1)2x(20-2x)+2x(16-2x)=160.
(2)按要求整理,得x2-9x+20=0,其中一次项系数是-9,常数项是20.
https://www.21cnjy.com/help/help_extract.php
21.1 一元二次方程
第二十一章
一元二次方程
21.1 一元二次方程
预学浅梳理
探究与应用
随堂小检测
第二十一章 一元二次方程
1.观察方程2x2=1,x2-2x=0,4y2=y+1,它们等号的两边都
是________式,方程中都只含有________个未知数,并且未
知数的最高次数是________,像这样的方程,叫做一元二次
方程.
整
一
2
2.一元二次方程的一般形式是ax2+bx+c=0(a≠0),其中
________是二次项,________是二次项系数;________是一
次项,________是一次项系数;________是常数项.
3.使方程左右两边________的未知数的值就是这个一元二
次方程的解,一元二次方程的解也叫做一元二次方程的
________.
ax2
a
bx
b
c
相等
根
目标一 理解一元二次方程的概念
问题1
如图21-1-1,有一块矩形铁皮,长100
cm,宽50
cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3600
cm2,那么铁皮各角应切去多大的正方形?(要求只列出方程)
图21-1-1
探究
设切去的正方形的边长为x
cm,则盒底的长为
___________,宽为___________,得方程_________________
________,整理得_________________.
(100-2x)cm
(50-2x)cm
(100-2x)(50-2x)
=3600
x2-75x+350=0
图21-1-1
问题2
要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?(要求只列出方程)
探究
全部比赛的场数为_________.
设应邀请x个队参赛,每个队要与其他(x-1)个队各赛1场,所以全部比赛共_________场.列方程____________,化简整理得___________.
7×4=28
x2-x=56
思考
观察问题1与问题2中得出的方程及方程x2+2x-4=0,5y2+y=0,2y2=18,你发现它们的共同点是什么?
解:共同点:方程中等号的两边都是整式,方程中只含有一个未知数,并且未知数的最高次数是2.
定义
等号两边都是整式,只含有________个未知数,并且未知数的____________是2的方程,叫做一元二次方程.
一
最高次数
C
归纳
判定一元二次方程的关键要素
方程中
(1)等号两边都是________;
(2)____________未知数;
(3)未知数的最高次数是________.
整式
只含有一个
2
目标二 掌握一元二次方程的一般形式,正确认识二次项
系数、一次项系数及常数项
问题3
将前面思考中的五个方程的各项都移到等号的左边,并按所含未知数的降幂排列,等号右边变为0,它们是否都符合ax2+bx+c=0(a≠0)的形式?把它们化成ax2+bx+c=0形式后的二次项系数、一次项系数、常数项分别是什么?
解:方程x2-75x+350=0符合ax2+bx+c=0(a≠0)的形式,它的二次项系数是1,一次项系数是-75,常数项是350;方程x2-x=56整理,得x2-x-56=0,符合ax2+bx+c=0(a≠0)的形式,方程x2-x-56=0的二次项系数是1,一次项系数是-1,常数项是-56;方程x2+2x-4=0符合ax2+bx+c=0(a≠0)的形式,它的二次项系数是1,一次项系数是2,常数项是-4;5y2+y=0符合ax2+bx+c=0(a≠0)的形式,它的二次项系数是5,一次项系数是1,常数项是0;2y2=18化成一般形式是2y2-18=0,符合ax2+bx+c=0(a≠0)的形式,它的二次项系数是2,一次项系数是0,常数项是-18.
总结
一元二次方程的一般形式
ax2+bx+c=0(a≠0)
二次项
系数
一次项
系数
常数项
例2
[教材P3例题]将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项.
解:去括号,得3x2-3x=5x+10.
移项,合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
其中二次项系数为3,一次项系数为-8,常数项为-10.
变式1
方程x2-2(3x-2)+(x+1)=0的一般形式是( )
A.x2-5x+5=0
B.x2+5x+5=0
C.x2+5x-5=0
D.x2+5=0
A
变式2
一个关于x的一元二次方程,它的二次项系数为3,一次项系数为2,常数项为-6,则这个一元二次方程是________________.
3x2+2x-6=0
目标三 理解一元二次方程根的意义
例3
下列哪些数是方程x2+2x-8=0的根?
-4,-3,0,2,4.
解:将x=-4代入方程x2+2x-8=0,左边=(-4)2+(-4)×2-8=0,即左边=右边,故-4是方程x2+2x-8=0的根.
同理可得,-3,0,4都不是方程x2+2x-8=0的根.
将x=2代入方程x2+2x-8=0,左边=22+2×2-8=0,即左边=右边,故2是方程x2+2x-8=0的根.
拓展
若关于x的一元二次方程(a-1)x2+x+|a|-1=0的一个根是0,则实数a的值是________.
[解析]
依题意,得|a|-1=0且a-1≠0,解得a=-1.
-1
拓展
已知关于x的方程x2+bx+a=0的一个根是x=-a
(a≠0),则a-b的值为(
)
A.-1
B.0
C.1
D.2
A
A
2.一元二次方程2y2-7=3y的二次项系数、一次项系数、常数项分别是( )
A.2,-3,-7
B.-2,-3,-7
C.2,-7,3
D.-2,-3,7
[解析]
2y2-7=3y,整理,得2y2-3y-7=0,
所以一元二次方程2y2-7=3y的二次项系数、一次项系数、常数项分别是2,-3,-7.
A
3.已知关于x的方程x2-mx+1=0的一个根为1,那么m的值是________.
[解析]
将x=1代入方程x2-mx+1=0,得12-m+1=0,
即2-m=0,
解得m=2.
2
图21-1-2
解:(1)2x(20-2x)+2x(16-2x)=160.
(2)按要求整理,得x2-9x+20=0,其中一次项系数是-9,常数项是20.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
