【人教九上数学学霸听课笔记】21.2.2 公式法 课件(共34张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】21.2.2 公式法 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 00:00:00 | ||
图片预览





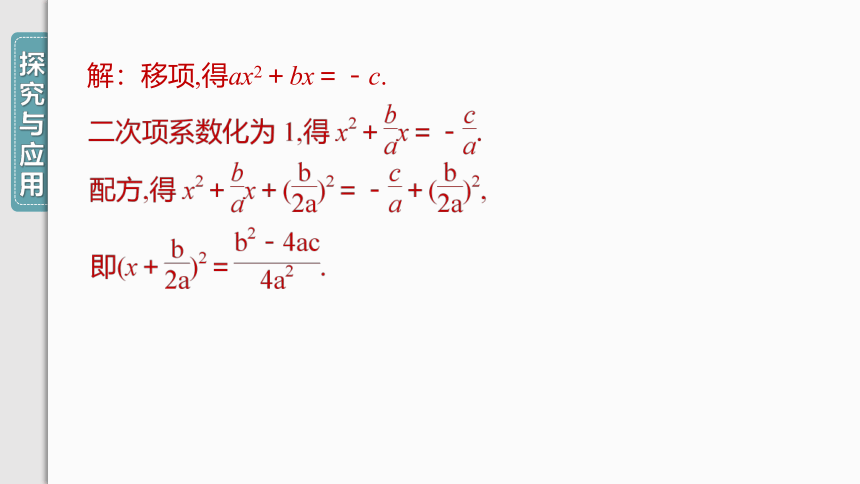






文档简介
(共32张PPT)
21.2 解一元二次方程
第二十一章
一元二次方程
21.2.2 公式法
预学浅梳理
探究与应用
随堂小检测
第二十一章 一元二次方程
1.一元二次方程ax2+bx+c=0(a≠0)根的判别式Δ=
________.
2.当Δ>0时,方程ax2+bx+c=0(a≠0)有两个________的实数
根;当Δ=0时,方程ax2+bx+c=0(a≠0)有两个________的
实数根;当Δ<0时,方程ax2+bx+c=0(a≠0)_______实数根.
b2-4ac
不等
相等
无
当Δ________时,方程ax2+bx+c=0(a≠0)有实数根,其根可
写为x=_______________的形式,这个式子叫做一元二次方
程ax2+bx+c=0(a≠0)的求根公式.用求根公式解一元二次
的方法叫做________.
≥0
公式法
目标一 探究一元二次方程的求根公式
问题
用配方法解一元二次方程ax2+bx+c=0(a≠0).
(1)如何将方程ax2+bx+c=0的左边配成完全平方的形式?请写出配方过程.
解:移项,得ax2+bx=-c.
(2)配方后用直接开平方法求根,方程根的情况与什么有关?请继续写出根的求解过程.
解:方程根的情况与b2-4ac的值有关.
因为a≠0,所以4a2>0.
式子b2-4ac的值有以下三种情况:
1.一元二次方程ax2+bx+c=0(a≠0)的判别式与其根的情况
的关系
(1)____________?方程有两个不等的实数根;
(2)b2-4ac=0?方程有____________实数根;
(3)__________?方程无实数根.
归纳总结
b2-4ac>0
两个相等的
b2-4ac<0
2.一元二次方程ax2+bx+c=0(a≠0)的求根公式
当b2-4ac_______0时,x=______________.
归纳总结
≥
目标二 会用公式法解一元二次方程
例1
[教材P11例2]用公式法解下列方程:
(1)x2-4x-7=0;
[解析]
用公式法解一元二次方程时,一定要先写对a,b,c的值,再判断Δ的正负.
解:a=1,b=-4,c=-7.
Δ=b2-4ac=(-4)2-4×1×(-7)=44>0.
方程有两个相等的实数根
(3)5x2-3x=x+1;
解:方程化为5x2-4x-1=0.
a=5,b=-4,c=-1.
Δ=b2-4ac=(-4)2-4×5×(-1)=36>0.
方程有两个不等的实数根
(4)x2+17=8x.
解:方程化为x2-8x+17=0.
a=1,b=-8,c=17.
Δ=b2-4ac=(-8)2-4×1×17=-4<0.
方程无实数根.
归纳
用公式法解一元二次方程的“四步法”
把方程化成一般形式:
ax2+bx+c=0(a≠0)
确定a,b,
c的值
求b2-4ac的值
b2-4ac≧0
b2-4ac<0
将a,b,c的值代入求根
公式,求出方程的根
原方程没有实数根
目标三 理解一元二次方程根的判别式,能运用根的判别
式进行相关的计算或推理
例2
不解方程,判别下列方程的根的情况:
(1)x2-5x=-7;
解:方程变形为一元二次方程的一般形式为x2-5x+7=0.
∵a=1,b=-5,c=7,∴Δ=b2-4ac=(-5)2-4×1×7=-3<0,
故方程无实数根.
故方程有两个相等的实数根.
(3)(x-1)(2x+3)=x.
解:方程变形为一元二次方程的一般形式为2x2-3=0.
∵a=2,b=0,c=-3,
∴Δ=b2-4ac=02-4×2×(-3)=24>0,
故方程有两个不等的实数根.
拓展
已知关于x的一元二次方程(m-1)x2-(2m+1)x+m=0,求当m取何值时:
(1)方程有两个不相等的实数根;
(2)方程有两个相等的实数根,并求出根;
(3)方程没有实数根.
解:(1)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个不相等的实数根,
∴Δ=[-(2m+1)]2-4(m-1)m>0,且m-1≠0,
(2)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个相等的实数根,
(3)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0没有实数根,
∴Δ=[-(2m+1)]2-4(m-1)m<0,
1.方程2x2-5x+3=0中,a=________,b=________,c=________.判别式Δ=b2-4ac=________.因为Δ________0,所以此方程有两个________的实数根.
2
-5
3
1
>
不等
D
3.解方程:3x2+10x-5=3.
解:将原方程化为一元二次方程的一般形式,得______________.
这里a=________,b=________,c=________.
判别式Δ=b2-4ac=________-4×________×________=________>0,
3x2+10x-8=0
3
10
-8
102
3
(-8)
196
3
7
-4
10
4.用公式法解下列方程:
(1)2x(x-3)=-3x+5;
解:原方程可化为2x2-3x-5=0.
Δ=b2-4ac=(-3)2-4×2×(-5)=49>0.
(2)3y2+5(2y+3)=0.
解:原方程可化为3y2+10y+15=0.
Δ=b2-4ac=102-4×3×15=-80<0,
所以此方程无实数根.
https://www.21cnjy.com/help/help_extract.php
21.2 解一元二次方程
第二十一章
一元二次方程
21.2.2 公式法
预学浅梳理
探究与应用
随堂小检测
第二十一章 一元二次方程
1.一元二次方程ax2+bx+c=0(a≠0)根的判别式Δ=
________.
2.当Δ>0时,方程ax2+bx+c=0(a≠0)有两个________的实数
根;当Δ=0时,方程ax2+bx+c=0(a≠0)有两个________的
实数根;当Δ<0时,方程ax2+bx+c=0(a≠0)_______实数根.
b2-4ac
不等
相等
无
当Δ________时,方程ax2+bx+c=0(a≠0)有实数根,其根可
写为x=_______________的形式,这个式子叫做一元二次方
程ax2+bx+c=0(a≠0)的求根公式.用求根公式解一元二次
的方法叫做________.
≥0
公式法
目标一 探究一元二次方程的求根公式
问题
用配方法解一元二次方程ax2+bx+c=0(a≠0).
(1)如何将方程ax2+bx+c=0的左边配成完全平方的形式?请写出配方过程.
解:移项,得ax2+bx=-c.
(2)配方后用直接开平方法求根,方程根的情况与什么有关?请继续写出根的求解过程.
解:方程根的情况与b2-4ac的值有关.
因为a≠0,所以4a2>0.
式子b2-4ac的值有以下三种情况:
1.一元二次方程ax2+bx+c=0(a≠0)的判别式与其根的情况
的关系
(1)____________?方程有两个不等的实数根;
(2)b2-4ac=0?方程有____________实数根;
(3)__________?方程无实数根.
归纳总结
b2-4ac>0
两个相等的
b2-4ac<0
2.一元二次方程ax2+bx+c=0(a≠0)的求根公式
当b2-4ac_______0时,x=______________.
归纳总结
≥
目标二 会用公式法解一元二次方程
例1
[教材P11例2]用公式法解下列方程:
(1)x2-4x-7=0;
[解析]
用公式法解一元二次方程时,一定要先写对a,b,c的值,再判断Δ的正负.
解:a=1,b=-4,c=-7.
Δ=b2-4ac=(-4)2-4×1×(-7)=44>0.
方程有两个相等的实数根
(3)5x2-3x=x+1;
解:方程化为5x2-4x-1=0.
a=5,b=-4,c=-1.
Δ=b2-4ac=(-4)2-4×5×(-1)=36>0.
方程有两个不等的实数根
(4)x2+17=8x.
解:方程化为x2-8x+17=0.
a=1,b=-8,c=17.
Δ=b2-4ac=(-8)2-4×1×17=-4<0.
方程无实数根.
归纳
用公式法解一元二次方程的“四步法”
把方程化成一般形式:
ax2+bx+c=0(a≠0)
确定a,b,
c的值
求b2-4ac的值
b2-4ac≧0
b2-4ac<0
将a,b,c的值代入求根
公式,求出方程的根
原方程没有实数根
目标三 理解一元二次方程根的判别式,能运用根的判别
式进行相关的计算或推理
例2
不解方程,判别下列方程的根的情况:
(1)x2-5x=-7;
解:方程变形为一元二次方程的一般形式为x2-5x+7=0.
∵a=1,b=-5,c=7,∴Δ=b2-4ac=(-5)2-4×1×7=-3<0,
故方程无实数根.
故方程有两个相等的实数根.
(3)(x-1)(2x+3)=x.
解:方程变形为一元二次方程的一般形式为2x2-3=0.
∵a=2,b=0,c=-3,
∴Δ=b2-4ac=02-4×2×(-3)=24>0,
故方程有两个不等的实数根.
拓展
已知关于x的一元二次方程(m-1)x2-(2m+1)x+m=0,求当m取何值时:
(1)方程有两个不相等的实数根;
(2)方程有两个相等的实数根,并求出根;
(3)方程没有实数根.
解:(1)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个不相等的实数根,
∴Δ=[-(2m+1)]2-4(m-1)m>0,且m-1≠0,
(2)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0有两个相等的实数根,
(3)∵关于x的一元二次方程(m-1)x2-(2m+1)x+m=0没有实数根,
∴Δ=[-(2m+1)]2-4(m-1)m<0,
1.方程2x2-5x+3=0中,a=________,b=________,c=________.判别式Δ=b2-4ac=________.因为Δ________0,所以此方程有两个________的实数根.
2
-5
3
1
>
不等
D
3.解方程:3x2+10x-5=3.
解:将原方程化为一元二次方程的一般形式,得______________.
这里a=________,b=________,c=________.
判别式Δ=b2-4ac=________-4×________×________=________>0,
3x2+10x-8=0
3
10
-8
102
3
(-8)
196
3
7
-4
10
4.用公式法解下列方程:
(1)2x(x-3)=-3x+5;
解:原方程可化为2x2-3x-5=0.
Δ=b2-4ac=(-3)2-4×2×(-5)=49>0.
(2)3y2+5(2y+3)=0.
解:原方程可化为3y2+10y+15=0.
Δ=b2-4ac=102-4×3×15=-80<0,
所以此方程无实数根.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
