24.2.2直线和圆的位置关系 切线长定理 学案 2021--2022学年人教版九年级数学上册
文档属性
| 名称 | 24.2.2直线和圆的位置关系 切线长定理 学案 2021--2022学年人教版九年级数学上册 |

|
|
| 格式 | zip | ||
| 文件大小 | 98.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 00:00:00 | ||
图片预览

文档简介
24.2.2 直线和圆的位置关系
第3课时 切线长定理
学习目标
1.掌握切线长定理,初步学会运用切线长定理进行计算与证明.
2.了解有关三角形的内切圆和三角形的内心的概念.
3.学会利用方程思想解决几何问题,体验数形结合思想.
自主探究
探究点一:切线长定理
例1、如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上.若PA长为2,则△PEF的周长是________.
探究点二:三角形的内切圆
例2、如图,⊙O是边长为2的等边△ABC的内切圆,则⊙O的半径为________.
尝试应用
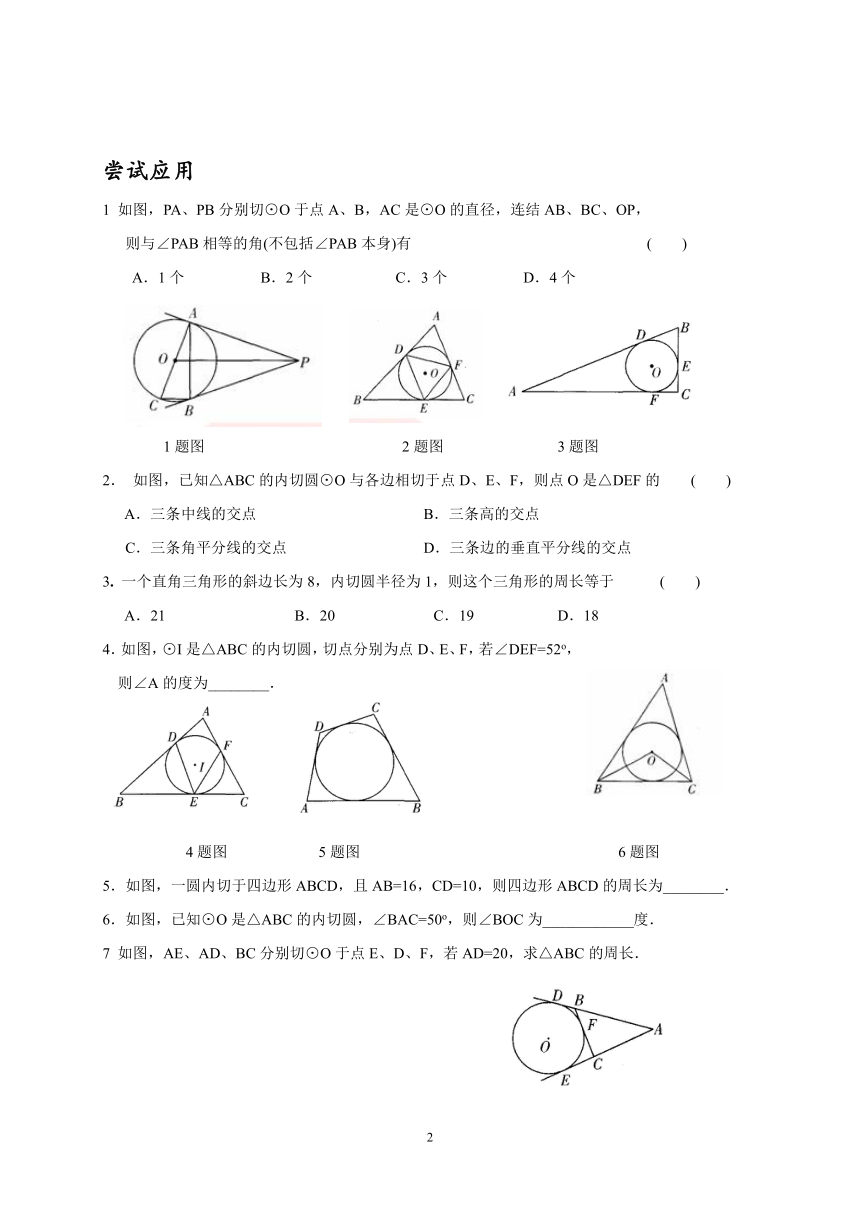
1
如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,
则与∠PAB相等的角(不包括∠PAB本身)有
(
)
A.1个
B.2个
C.3个
D.4个
1题图
2题图
3题图
2.
如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的
(
)
A.三条中线的交点
B.三条高的交点
C.三条角平分线的交点
D.三条边的垂直平分线的交点
3.
一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于
(
)
A.21
B.20
C.19
D.18
4.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,
则∠A的度为________.
4题图
5题图
6题图
5.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
6.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.
7
如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
8
如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC=
12,∠P=60o,求弦AB的长.
9.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
10.已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.
11.已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.
12.如图所示,PA、PB是⊙O的两条切线,A、B为切点,求证:∠ABO=∠APB。
13.如图,EB、EC是⊙O的两条切线,B、C是切点,
A、D是⊙O上两点,如果∠E=46°,
∠DCF=32°,求∠A的度数。
课堂小结
通过今天的学习,你有什么收获?
课后作业
PAGE
1
第3课时 切线长定理
学习目标
1.掌握切线长定理,初步学会运用切线长定理进行计算与证明.
2.了解有关三角形的内切圆和三角形的内心的概念.
3.学会利用方程思想解决几何问题,体验数形结合思想.
自主探究
探究点一:切线长定理
例1、如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上.若PA长为2,则△PEF的周长是________.
探究点二:三角形的内切圆
例2、如图,⊙O是边长为2的等边△ABC的内切圆,则⊙O的半径为________.
尝试应用
1
如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,
则与∠PAB相等的角(不包括∠PAB本身)有
(
)
A.1个
B.2个
C.3个
D.4个
1题图
2题图
3题图
2.
如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的
(
)
A.三条中线的交点
B.三条高的交点
C.三条角平分线的交点
D.三条边的垂直平分线的交点
3.
一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于
(
)
A.21
B.20
C.19
D.18
4.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,
则∠A的度为________.
4题图
5题图
6题图
5.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
6.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.
7
如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
8
如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC=
12,∠P=60o,求弦AB的长.
9.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
10.已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.
11.已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.
12.如图所示,PA、PB是⊙O的两条切线,A、B为切点,求证:∠ABO=∠APB。
13.如图,EB、EC是⊙O的两条切线,B、C是切点,
A、D是⊙O上两点,如果∠E=46°,
∠DCF=32°,求∠A的度数。
课堂小结
通过今天的学习,你有什么收获?
课后作业
PAGE
1
同课章节目录
