2020-2021学年 人教九年级数学上册24.2.2直线与圆的位置关系教案
文档属性
| 名称 | 2020-2021学年 人教九年级数学上册24.2.2直线与圆的位置关系教案 |  | |
| 格式 | zip | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 05:57:23 | ||
图片预览

文档简介
24.2.2
直线与圆的位置关系(适用于平行班)
教学目标:经历直线与圆不同位置关系的探索过程,掌握直线与圆的位置关系,以及利用圆心到直线距离进行判断。
教学重点:从图像里抽象出几何图案,展开对直线与圆位置关系的探究.
教学难点:直线与圆的三种位置关系及其判断方式
教学过程:
环节
内容
素养培养
教师导学
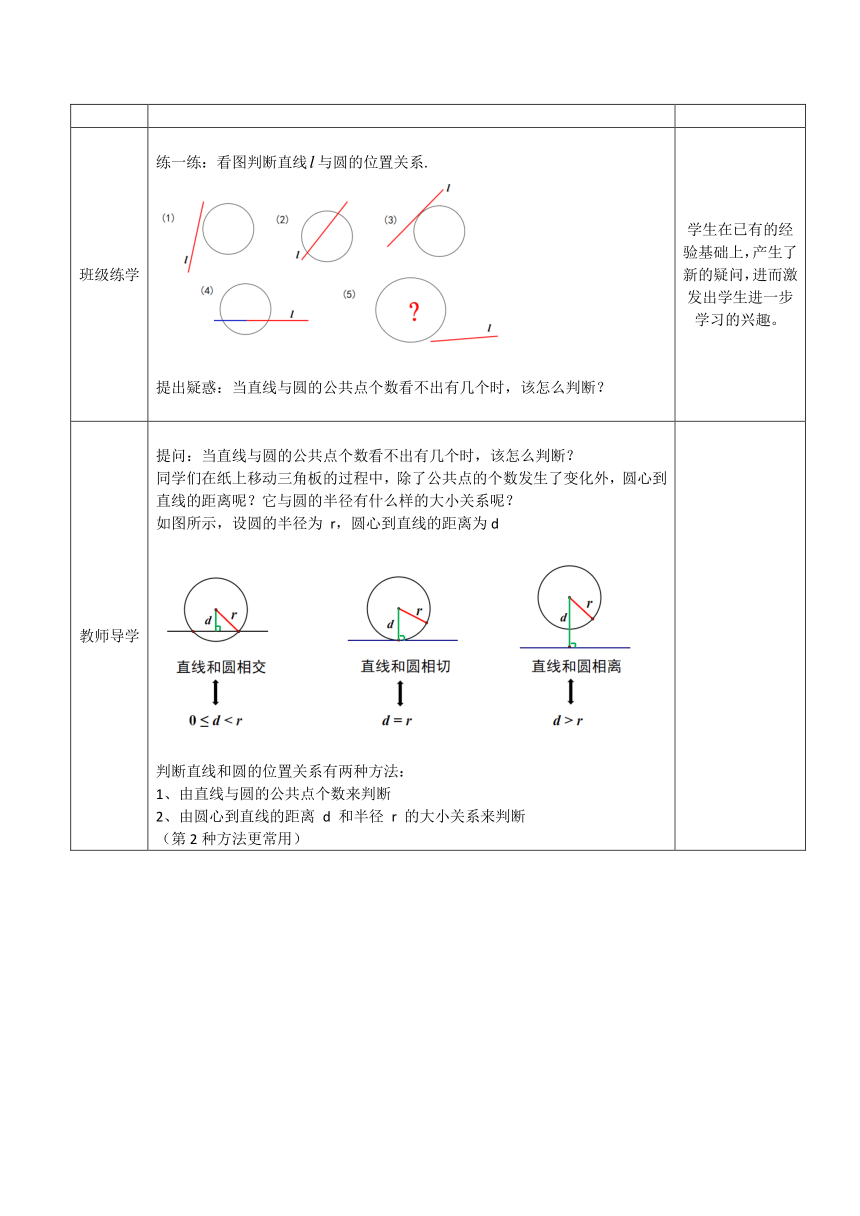
1、“大漠孤烟直,长河落日圆”是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?2、请同学在纸上画一个圆,移动三角板,观察三角板一条直角边所在直线和圆的公共点情况。公共点个数最少时有几个?最多时有几个?
通过古诗和实际情境引出课题,既丰富了学生的语文知识,又培养了学生直观想象的数学核心素养。
教师总学
总结归纳上述结果,并将其填入表中:要点归纳:直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图直线),这个唯一的公共点叫做切点(如图点A).
班级练学
练一练:看图判断直线与圆的位置关系.提出疑惑:当直线与圆的公共点个数看不出有几个时,该怎么判断?
学生在已有的经验基础上,产生了新的疑问,进而激发出学生进一步学习的兴趣。
教师导学
提问:当直线与圆的公共点个数看不出有几个时,该怎么判断?同学们在纸上移动三角板的过程中,除了公共点的个数发生了变化外,圆心到直线的距离呢?它与圆的半径有什么样的大小关系呢?如图所示,设圆的半径为
r,圆心到直线的距离为d判断直线和圆的位置关系有两种方法:1、由直线与圆的公共点个数来判断2、由圆心到直线的距离
d
和半径
r
的大小关系来判断(第2种方法更常用)
班级练学
练一练:1.已知圆的半径为6cm,设直线和圆心的距离为d
:(1)若d=4cm
,则直线与圆____,
直线与圆有____个公共点.
(2)若d=6m
,则直线与圆____,
直线与圆有____个公共点.
(3)若d=8cm
,则直线与圆____,
直线与圆有____个公共点.
2.已知⊙O的半径为5cm,
圆心O与直线AB的距离为dcm,
根据条件填写d的范围:
(1)若AB和⊙O相离,
则
_______________
;
(2)若AB和⊙O相切,
则
_______________
;(3)若AB和⊙O相交,
则
_______________
.
由学生以“快问快答”的方式迅速说出答案,巩固以上知识。
精选练学
例1、如图,在Rt△AOC中,∠ACB
=
90°,AC=6cm,BC=8cm,以C为圆心,r为半径的圆,与直线AB有何位置关系?为什么?(1)
r=8cm;(2)
r=4.8cm;
(3)
r=6cm.例2、
如图,∠AOB
=
30°,P为OB上一点,OP=5,以P为圆心,r为半径作圆,分别在下列条件下判断直线OA与⊙P的位置关系。(1)
r=2;(2)
r=2.5;
(3)
r=3.分析:要了解OA与⊙P的位置关系,只要知道圆心P到OA的距离d与r的关系.所以需求出P到OA的距离d.
在基础知识上稍加变化,注重知识的综合运用。
小组展学
拓展1、已知⊙A的直径为6,点A的坐标为(-3,-4),(1)
则轴与⊙A的位置关系是_________,
轴与⊙A的位置关系是________.(2)
若⊙A要与轴相切,则⊙A该向上移动________
个单位.(3)
若⊙A要与轴相交,设⊙A向上平移个单位,
则的取值范围是
.拓展2、Rt△ABC,∠C=90°AC=3,BC=4,以C为圆心画圆,
(1)当半径r为何范围时,圆C与线段AB没有公共点?(2)当半径r为何范围时,圆C与线段AB有一个公共点?
(3)当半径r为何范围时,圆C与线段AB有两个公共点?拓展3、以坐标原点O为圆心,作半径为3的圆,若直线与⊙O相交,则的取值范围是
.
运用动画和几何画板的形式,直观和清晰的展示出动点问题以及范围问题的图形,加深学生对此类题目的理解和思考。
教师总学
1、直线与圆的位置关系
2、用圆心O到直线的距离d与圆的半径r的大小关系来判断:
作业布置
练习册67页、68页
板书设计
拓展3
直线与圆没有公共点
相离
直线与圆有一个公共点
相切
直线与圆有两个公共点
相交
相离
相切
相交
d>r
d=r
d24.2.2
直线与圆的位置关系
例1
直线与圆的位置关系(适用于平行班)
教学目标:经历直线与圆不同位置关系的探索过程,掌握直线与圆的位置关系,以及利用圆心到直线距离进行判断。
教学重点:从图像里抽象出几何图案,展开对直线与圆位置关系的探究.
教学难点:直线与圆的三种位置关系及其判断方式
教学过程:
环节
内容
素养培养
教师导学
1、“大漠孤烟直,长河落日圆”是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?2、请同学在纸上画一个圆,移动三角板,观察三角板一条直角边所在直线和圆的公共点情况。公共点个数最少时有几个?最多时有几个?
通过古诗和实际情境引出课题,既丰富了学生的语文知识,又培养了学生直观想象的数学核心素养。
教师总学
总结归纳上述结果,并将其填入表中:要点归纳:直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图直线),这个唯一的公共点叫做切点(如图点A).
班级练学
练一练:看图判断直线与圆的位置关系.提出疑惑:当直线与圆的公共点个数看不出有几个时,该怎么判断?
学生在已有的经验基础上,产生了新的疑问,进而激发出学生进一步学习的兴趣。
教师导学
提问:当直线与圆的公共点个数看不出有几个时,该怎么判断?同学们在纸上移动三角板的过程中,除了公共点的个数发生了变化外,圆心到直线的距离呢?它与圆的半径有什么样的大小关系呢?如图所示,设圆的半径为
r,圆心到直线的距离为d判断直线和圆的位置关系有两种方法:1、由直线与圆的公共点个数来判断2、由圆心到直线的距离
d
和半径
r
的大小关系来判断(第2种方法更常用)
班级练学
练一练:1.已知圆的半径为6cm,设直线和圆心的距离为d
:(1)若d=4cm
,则直线与圆____,
直线与圆有____个公共点.
(2)若d=6m
,则直线与圆____,
直线与圆有____个公共点.
(3)若d=8cm
,则直线与圆____,
直线与圆有____个公共点.
2.已知⊙O的半径为5cm,
圆心O与直线AB的距离为dcm,
根据条件填写d的范围:
(1)若AB和⊙O相离,
则
_______________
;
(2)若AB和⊙O相切,
则
_______________
;(3)若AB和⊙O相交,
则
_______________
.
由学生以“快问快答”的方式迅速说出答案,巩固以上知识。
精选练学
例1、如图,在Rt△AOC中,∠ACB
=
90°,AC=6cm,BC=8cm,以C为圆心,r为半径的圆,与直线AB有何位置关系?为什么?(1)
r=8cm;(2)
r=4.8cm;
(3)
r=6cm.例2、
如图,∠AOB
=
30°,P为OB上一点,OP=5,以P为圆心,r为半径作圆,分别在下列条件下判断直线OA与⊙P的位置关系。(1)
r=2;(2)
r=2.5;
(3)
r=3.分析:要了解OA与⊙P的位置关系,只要知道圆心P到OA的距离d与r的关系.所以需求出P到OA的距离d.
在基础知识上稍加变化,注重知识的综合运用。
小组展学
拓展1、已知⊙A的直径为6,点A的坐标为(-3,-4),(1)
则轴与⊙A的位置关系是_________,
轴与⊙A的位置关系是________.(2)
若⊙A要与轴相切,则⊙A该向上移动________
个单位.(3)
若⊙A要与轴相交,设⊙A向上平移个单位,
则的取值范围是
.拓展2、Rt△ABC,∠C=90°AC=3,BC=4,以C为圆心画圆,
(1)当半径r为何范围时,圆C与线段AB没有公共点?(2)当半径r为何范围时,圆C与线段AB有一个公共点?
(3)当半径r为何范围时,圆C与线段AB有两个公共点?拓展3、以坐标原点O为圆心,作半径为3的圆,若直线与⊙O相交,则的取值范围是
.
运用动画和几何画板的形式,直观和清晰的展示出动点问题以及范围问题的图形,加深学生对此类题目的理解和思考。
教师总学
1、直线与圆的位置关系
2、用圆心O到直线的距离d与圆的半径r的大小关系来判断:
作业布置
练习册67页、68页
板书设计
拓展3
直线与圆没有公共点
相离
直线与圆有一个公共点
相切
直线与圆有两个公共点
相交
相离
相切
相交
d>r
d=r
d
直线与圆的位置关系
例1
同课章节目录
