人教版九年级上册24.3正多方形与圆【教案】
文档属性
| 名称 | 人教版九年级上册24.3正多方形与圆【教案】 |

|
|
| 格式 | zip | ||
| 文件大小 | 148.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 00:00:00 | ||
图片预览


文档简介
教案
教
师:
初(高)
学生:
上课时间
年
月
日
阶
段:
基础(
)
提高(
)
强化(
)
课时计划
共
次课
第
次课
教学课题:
正多边形和圆
教学目标:
1、了解正多边形和圆的有关概念;理解并掌握正多边形半径和边长、边心距、中心角之间的关系2、使学生知道正多边形的对称性,对称轴。了解用量角器等分圆心角来等分圆,从而可以作出圆内接或圆外切正多边形.使学生会用尺规作圆内接正方形和正六边形,在这个基础上能作圆内接正八边形、正三角形、正十二边形
教学重难点:
重点:用量角器等分圆心角来等分圆,然后作出圆内接或圆外切正多边形;用尺规作圆内接正方形和正六边形.难点:准确作图
教学过程
一、预习并完成下列习题重要概念:(1)各边
,各角也
的多边形是正多边形.(2)一个正多边形的
叫做这个多边形的中心.(3)
的半径叫做正多边形的半径.(4)
正多边形每一边所对的
角叫做正多边形的中心角.(5)中心到正多边形的一边的距离叫做正多边形的
.(6)正多边形内切圆的半径就是正多边形的
,外接圆的半径就是正多边形的
.练习:(1)判断题:①各边相等的圆外切多边形一定是正多边形.(
)②各角相等的圆内接多边形一定是正多边形.(
)③正多边形的中心角等于它的每一个外角.(
)④若一个正多边形的每一个内角是150°,则这个正多边形是正十二边形.(
)⑤各角相等的圆外切多边形是正多边形.(
)(2)
填空题:①一个外角等于它的一个内角的正多边形是正____边形.②正八边形的中心角的度数为____,每一个内角度数为____,每一个外角度数为____.③边长为6cm的正三角形的半径是____cm,边心距是____cm,面积是____cm.
④半径是2cm的正六边形的边长是____,边心距是
,周长是
。
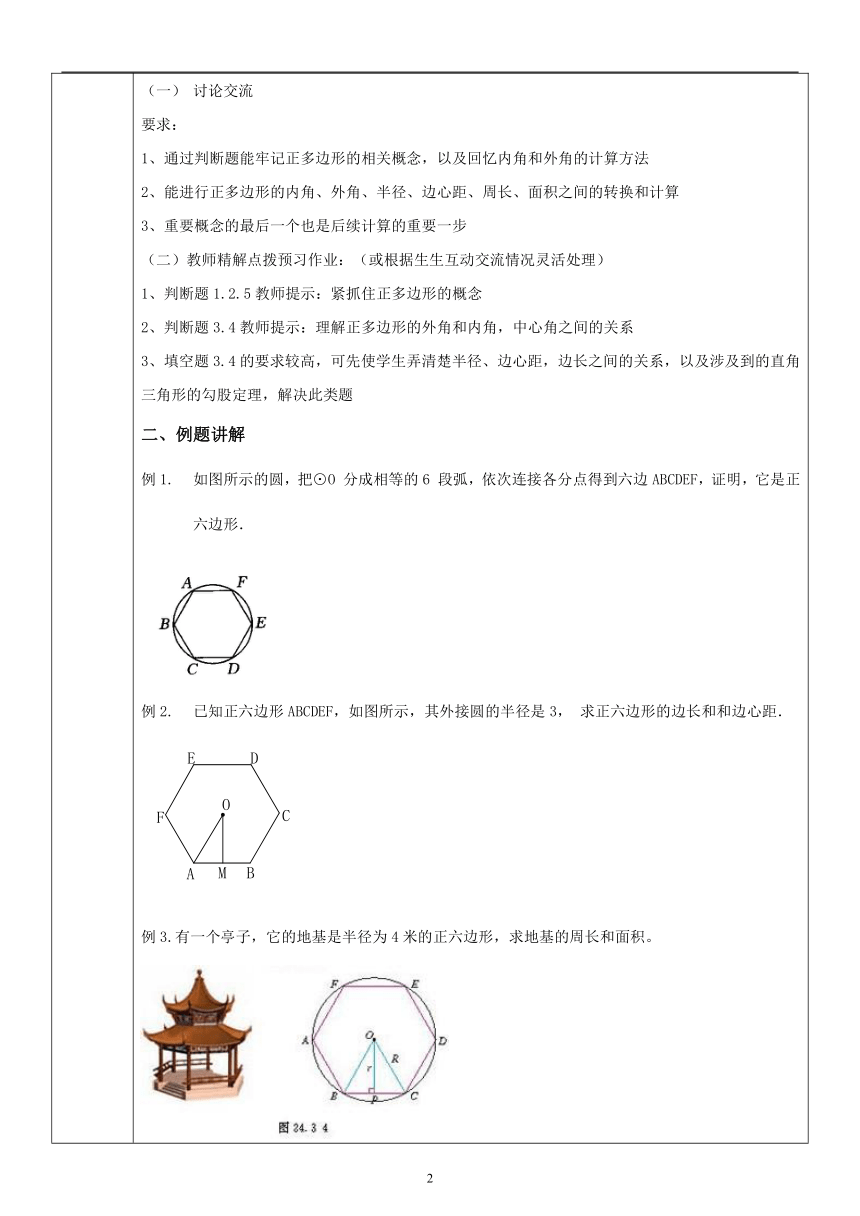
讨论交流要求:1、通过判断题能牢记正多边形的相关概念,以及回忆内角和外角的计算方法2、能进行正多边形的内角、外角、半径、边心距、周长、面积之间的转换和计算3、重要概念的最后一个也是后续计算的重要一步(二)教师精解点拨预习作业:(或根据生生互动交流情况灵活处理)1、判断题1.2.5教师提示:紧抓住正多边形的概念2、判断题3.4教师提示:理解正多边形的外角和内角,中心角之间的关系3、填空题3.4的要求较高,可先使学生弄清楚半径、边心距,边长之间的关系,以及涉及到的直角三角形的勾股定理,解决此类题二、例题讲解如图所示的圆,把⊙O分成相等的6段弧,依次连接各分点得到六边ABCDEF,证明,它是正六边形.已知正六边形ABCDEF,如图所示,其外接圆的半径是3,求正六边形的边长和和边心距.例3.有一个亭子,它的地基是半径为4米的正六边形,求地基的周长和面积。预习在正三角形、正方形、正五边形、正六边形、正七边形、正八边形中,哪些正多边形是轴对称图形,哪些是中心对称图形?哪些正多边形既是轴对称图形,又是中心对称图形?有何规律?分别说出其对称轴或对称中心。画圆的内接正多边形方法指导:(1)由于同圆中相等的圆心角所对的
相等,因此做相等的
就可以等分圆,从而得到相应的正多边形例如:画一个边长为2cm的正六边形时,我们可以以
为半径做一个⊙O,用量角器画一个等于=
圆心角,它对着一段弧,然后在圆上依次截取
,就得到圆的
个等分点,
连接各分点,即可得出正六边形。(仿照下图,自己画一遍。)(2)对于一些特殊的正多边形,还可以用
和
来作。
例如:我们可以这样作正六边形,由于正六边形的边长等于半径,所以在半径为R的圆上依次截取等于
的弦,就可以将圆
等分,顺次连接各分点即可得到半径为R的正六边形。再如,用直尺和圆规做两条互相垂直的直径,就可以把圆
等分,从而作出
。例1、
用量角器画出半径为2cm的圆内接正九边形例2.
用尺规作图画出边心距为2的圆的内接正六边形,并在此图中再画出边心距为2的正三角形例3、已知⊙O和⊙O上的一点A,如图所示.(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;(2)在(1)题的作图中,如果点E在上,求证:DE是⊙O内接正十二边形的一边.当堂检测题:1.(1)利用你手中的工具画半径为2cm的圆内接正十二边形(2)做出边心距为cm的圆内接正六边形
课后作业
选择题:、1、下列命题中,假命题的是(
)
A.各边相等的圆内接多边形是正多边形.
B.正多边形的任意两个角的平分线如果相交,则交点为正多边形的中心.
C.正多边形的任意两条边的中垂线如果相交,则交点是正多边形的中心.
D.一个外角小于一个内角的正多边形一定是正五边形.2、正六边形的两条平行边间距离是1,则边长是(
)
A.
B.
C.
D.3、半径相等的圆内接正三角形、正方形、正六边形的边长之比为(
)A、1::
B、
::1
C、3:2:1
D、1:2:34、周长相等的正方形与正六边形的面积为S1
、S2,则S1
和
S2
的关系为(
)A、S1
<
S2
B、S1
=
S2
C、
S1
>
S2
D、无法确定5.如要想把边长12的等边三角形纸板剪去三个全等的小等边三角形,得到正六边形,则这个正六边形的边长是(??)
A.6????B.4????C.8?????D.9二、填空题1、正方形
正多边形;正三角形
正多边形;菱形
正多边形。(填“是”或“不是”)2、)一个正五边形要绕它的中心至少转
度,才能和原来的正五边形重合,在不超过360度的范围内有
个。3、有一个边长为3cm的正六边形,若要剪一张圆形纸片完全盖住这个正六边形,则这个圆形纸片的最小半径为
。4.
正方形ABCD内接于⊙O,点E在AD弧上,则∠BEC=
解答题1.
观察圆内接正五边形ABCDE(如图),解答下列问题:(1)图中以AB为底,且顶角为36°的等腰三角形有多少个?以AB为腰,且顶角为36°的等腰三角形有多少个?请分别将它们表示出来。(2)图中以AB为底,且底角为36°的等腰三角形有多少个?以AB为腰,且底角为36°的等腰三角形有多少个?请分别将它们表示出来。2.如图⑴⑵⑶⑷,M,N分别为⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,…正n边形ABCDE…的边AB,BC上的点,且BM=CN,连结OM,ON,⑴
求图⑴中∠MON的度数⑵
图⑵中∠MON的度数是
。
⑶
请探究∠MON的度数与正n边形边数n的关系为
。3.
如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走。按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是多少度4.
在半径为4的⊙O
中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积
2
教
师:
初(高)
学生:
上课时间
年
月
日
阶
段:
基础(
)
提高(
)
强化(
)
课时计划
共
次课
第
次课
教学课题:
正多边形和圆
教学目标:
1、了解正多边形和圆的有关概念;理解并掌握正多边形半径和边长、边心距、中心角之间的关系2、使学生知道正多边形的对称性,对称轴。了解用量角器等分圆心角来等分圆,从而可以作出圆内接或圆外切正多边形.使学生会用尺规作圆内接正方形和正六边形,在这个基础上能作圆内接正八边形、正三角形、正十二边形
教学重难点:
重点:用量角器等分圆心角来等分圆,然后作出圆内接或圆外切正多边形;用尺规作圆内接正方形和正六边形.难点:准确作图
教学过程
一、预习并完成下列习题重要概念:(1)各边
,各角也
的多边形是正多边形.(2)一个正多边形的
叫做这个多边形的中心.(3)
的半径叫做正多边形的半径.(4)
正多边形每一边所对的
角叫做正多边形的中心角.(5)中心到正多边形的一边的距离叫做正多边形的
.(6)正多边形内切圆的半径就是正多边形的
,外接圆的半径就是正多边形的
.练习:(1)判断题:①各边相等的圆外切多边形一定是正多边形.(
)②各角相等的圆内接多边形一定是正多边形.(
)③正多边形的中心角等于它的每一个外角.(
)④若一个正多边形的每一个内角是150°,则这个正多边形是正十二边形.(
)⑤各角相等的圆外切多边形是正多边形.(
)(2)
填空题:①一个外角等于它的一个内角的正多边形是正____边形.②正八边形的中心角的度数为____,每一个内角度数为____,每一个外角度数为____.③边长为6cm的正三角形的半径是____cm,边心距是____cm,面积是____cm.
④半径是2cm的正六边形的边长是____,边心距是
,周长是
。
讨论交流要求:1、通过判断题能牢记正多边形的相关概念,以及回忆内角和外角的计算方法2、能进行正多边形的内角、外角、半径、边心距、周长、面积之间的转换和计算3、重要概念的最后一个也是后续计算的重要一步(二)教师精解点拨预习作业:(或根据生生互动交流情况灵活处理)1、判断题1.2.5教师提示:紧抓住正多边形的概念2、判断题3.4教师提示:理解正多边形的外角和内角,中心角之间的关系3、填空题3.4的要求较高,可先使学生弄清楚半径、边心距,边长之间的关系,以及涉及到的直角三角形的勾股定理,解决此类题二、例题讲解如图所示的圆,把⊙O分成相等的6段弧,依次连接各分点得到六边ABCDEF,证明,它是正六边形.已知正六边形ABCDEF,如图所示,其外接圆的半径是3,求正六边形的边长和和边心距.例3.有一个亭子,它的地基是半径为4米的正六边形,求地基的周长和面积。预习在正三角形、正方形、正五边形、正六边形、正七边形、正八边形中,哪些正多边形是轴对称图形,哪些是中心对称图形?哪些正多边形既是轴对称图形,又是中心对称图形?有何规律?分别说出其对称轴或对称中心。画圆的内接正多边形方法指导:(1)由于同圆中相等的圆心角所对的
相等,因此做相等的
就可以等分圆,从而得到相应的正多边形例如:画一个边长为2cm的正六边形时,我们可以以
为半径做一个⊙O,用量角器画一个等于=
圆心角,它对着一段弧,然后在圆上依次截取
,就得到圆的
个等分点,
连接各分点,即可得出正六边形。(仿照下图,自己画一遍。)(2)对于一些特殊的正多边形,还可以用
和
来作。
例如:我们可以这样作正六边形,由于正六边形的边长等于半径,所以在半径为R的圆上依次截取等于
的弦,就可以将圆
等分,顺次连接各分点即可得到半径为R的正六边形。再如,用直尺和圆规做两条互相垂直的直径,就可以把圆
等分,从而作出
。例1、
用量角器画出半径为2cm的圆内接正九边形例2.
用尺规作图画出边心距为2的圆的内接正六边形,并在此图中再画出边心距为2的正三角形例3、已知⊙O和⊙O上的一点A,如图所示.(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;(2)在(1)题的作图中,如果点E在上,求证:DE是⊙O内接正十二边形的一边.当堂检测题:1.(1)利用你手中的工具画半径为2cm的圆内接正十二边形(2)做出边心距为cm的圆内接正六边形
课后作业
选择题:、1、下列命题中,假命题的是(
)
A.各边相等的圆内接多边形是正多边形.
B.正多边形的任意两个角的平分线如果相交,则交点为正多边形的中心.
C.正多边形的任意两条边的中垂线如果相交,则交点是正多边形的中心.
D.一个外角小于一个内角的正多边形一定是正五边形.2、正六边形的两条平行边间距离是1,则边长是(
)
A.
B.
C.
D.3、半径相等的圆内接正三角形、正方形、正六边形的边长之比为(
)A、1::
B、
::1
C、3:2:1
D、1:2:34、周长相等的正方形与正六边形的面积为S1
、S2,则S1
和
S2
的关系为(
)A、S1
<
S2
B、S1
=
S2
C、
S1
>
S2
D、无法确定5.如要想把边长12的等边三角形纸板剪去三个全等的小等边三角形,得到正六边形,则这个正六边形的边长是(??)
A.6????B.4????C.8?????D.9二、填空题1、正方形
正多边形;正三角形
正多边形;菱形
正多边形。(填“是”或“不是”)2、)一个正五边形要绕它的中心至少转
度,才能和原来的正五边形重合,在不超过360度的范围内有
个。3、有一个边长为3cm的正六边形,若要剪一张圆形纸片完全盖住这个正六边形,则这个圆形纸片的最小半径为
。4.
正方形ABCD内接于⊙O,点E在AD弧上,则∠BEC=
解答题1.
观察圆内接正五边形ABCDE(如图),解答下列问题:(1)图中以AB为底,且顶角为36°的等腰三角形有多少个?以AB为腰,且顶角为36°的等腰三角形有多少个?请分别将它们表示出来。(2)图中以AB为底,且底角为36°的等腰三角形有多少个?以AB为腰,且底角为36°的等腰三角形有多少个?请分别将它们表示出来。2.如图⑴⑵⑶⑷,M,N分别为⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,…正n边形ABCDE…的边AB,BC上的点,且BM=CN,连结OM,ON,⑴
求图⑴中∠MON的度数⑵
图⑵中∠MON的度数是
。
⑶
请探究∠MON的度数与正n边形边数n的关系为
。3.
如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走。按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是多少度4.
在半径为4的⊙O
中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积
2
同课章节目录
