人教版九年级数学上册:23.1 图形的旋转(习题课)【教案】
文档属性
| 名称 | 人教版九年级数学上册:23.1 图形的旋转(习题课)【教案】 |  | |
| 格式 | zip | ||
| 文件大小 | 91.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 08:01:29 | ||
图片预览

文档简介
九年级数学上册教学设计
课题
23.1
图形的旋转(习题课)
教学
目标
复习旋转的性质,能利用性质求角的度数或线段的长度。
教学
重点
旋转的性质
教学
难点
求角的度数或线段的长度
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
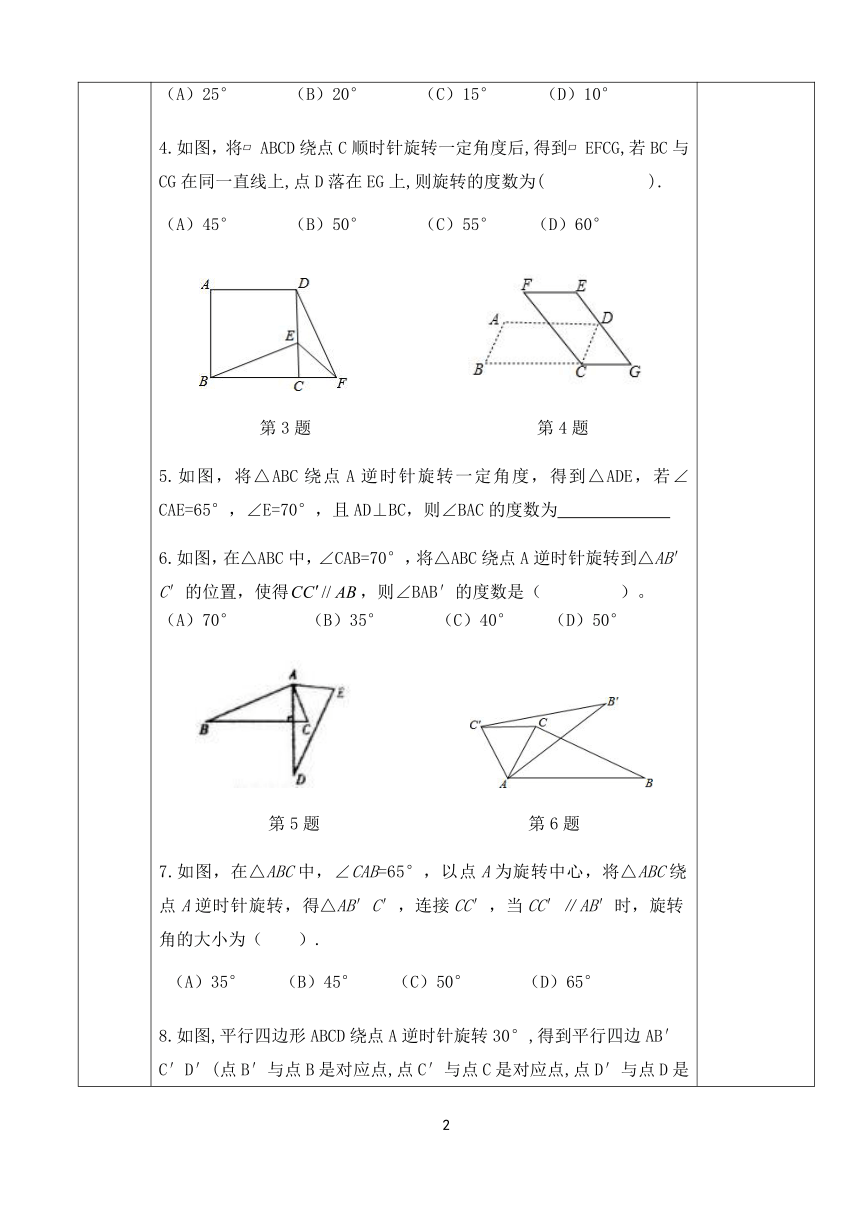
1.如图,△ABC和△ADE都是等腰直角三角形,其中;若△ADE经过旋转后能与△ABC重合,则旋转中心是A,旋转的角度是
度.
2.如图,已知点O是正△ABC三条高的交点,现将△AOB绕点O至少要旋转__________度后,与△BOC重合.
第1题
第2题
3.如图,在正方形ABCD中,E是DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF.若∠BEC=60°,则∠EFD的度数为(
).
(A)25°
(B)20°
(C)15°
(D)10°
4.如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为(?
???).
(A)45°
(B)50°
(C)55°
(D)60°
第3题
第4题
5.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为
6.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得,则∠BAB′的度数是(?
?)。
(A)70°
(B)35°
(C)40°
(D)50°
第5题
第6题
7.如图,在△ABC中,∠CAB=65°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB′C′,连接CC′,当CC′∥AB′时,旋转角的大小为( ).
(A)35°
(B)45°
(C)50°
(D)65°
8.如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C?的度数等于(??
??)
(A)100°
(B)105°
(C)115°
(D)120°
第7题
第8题
9.如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是(
)
(A)40°
(B)50°
(C)60°
(D)70°
10.如图,将Rt△ABC绕O点旋转90°,得Rt△BDE,其中∠ACB=∠BED=90°,AC=6,AB=10,则点C与其旋转中心点O的距离OC的长是(???
?)
(A)
(B)
(C)14
(D)12
第9题
第10题
11.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点P是△ABC内一点,AP=3,将△ABP绕点A逆时针旋转到△ACP′位置,求PP′的长是__________.
12.如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为?,1,?,?△ABP绕点B旋转至?△CBP′,连结PP′,并延长BP与DC相交于点Q,则?∠CPQ的大小为?_________(度)。
第11题
第12题
激趣导入,引入主题。
板
书
设
计
图形的旋转(习题课)
教
学
反
思
1
课题
23.1
图形的旋转(习题课)
教学
目标
复习旋转的性质,能利用性质求角的度数或线段的长度。
教学
重点
旋转的性质
教学
难点
求角的度数或线段的长度
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
1.如图,△ABC和△ADE都是等腰直角三角形,其中;若△ADE经过旋转后能与△ABC重合,则旋转中心是A,旋转的角度是
度.
2.如图,已知点O是正△ABC三条高的交点,现将△AOB绕点O至少要旋转__________度后,与△BOC重合.
第1题
第2题
3.如图,在正方形ABCD中,E是DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF.若∠BEC=60°,则∠EFD的度数为(
).
(A)25°
(B)20°
(C)15°
(D)10°
4.如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为(?
???).
(A)45°
(B)50°
(C)55°
(D)60°
第3题
第4题
5.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为
6.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得,则∠BAB′的度数是(?
?)。
(A)70°
(B)35°
(C)40°
(D)50°
第5题
第6题
7.如图,在△ABC中,∠CAB=65°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB′C′,连接CC′,当CC′∥AB′时,旋转角的大小为( ).
(A)35°
(B)45°
(C)50°
(D)65°
8.如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C?的度数等于(??
??)
(A)100°
(B)105°
(C)115°
(D)120°
第7题
第8题
9.如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是(
)
(A)40°
(B)50°
(C)60°
(D)70°
10.如图,将Rt△ABC绕O点旋转90°,得Rt△BDE,其中∠ACB=∠BED=90°,AC=6,AB=10,则点C与其旋转中心点O的距离OC的长是(???
?)
(A)
(B)
(C)14
(D)12
第9题
第10题
11.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点P是△ABC内一点,AP=3,将△ABP绕点A逆时针旋转到△ACP′位置,求PP′的长是__________.
12.如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为?,1,?,?△ABP绕点B旋转至?△CBP′,连结PP′,并延长BP与DC相交于点Q,则?∠CPQ的大小为?_________(度)。
第11题
第12题
激趣导入,引入主题。
板
书
设
计
图形的旋转(习题课)
教
学
反
思
1
同课章节目录
