《2.4圆周角》自主学习同步能力提升训练2021-2022学年苏科版九年级数学上册 (Word版 含答案)
文档属性
| 名称 | 《2.4圆周角》自主学习同步能力提升训练2021-2022学年苏科版九年级数学上册 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 532.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 21:12:33 | ||
图片预览



文档简介
2021年苏科版九年级数学上册《2.4圆周角》自主学习同步能力提升训练(附答案)
一.选择题(共6小题)
1.如图,AB是⊙O的直径,点C在⊙O上,∠OCA=40°,则∠BOC的度数为( )
A.80°
B.90°
C.100°
D.50°
2.如图,AB是⊙O的直径,点C,D在⊙O上,若∠D=110°,则∠BAC的度数为( )
A.20°
B.35°
C.55°
D.90°
3.如图,AB是半圆的直径,C、D是半圆上的两点,若∠ADC=125°,则∠BAC的度数是( )
A.25°
B.35°
C.45°
D.55°
4.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AB=3,则AD的值为( )
A.6
B.
C.5
D.
5.如图,点A、B、C、D在⊙O上,OB∥CD,∠A=25°,则∠BOD等于( )
A.100°
B.120°
C.130°
D.150°
6.如图,四边形ABCD内接于⊙O,DA=DC,若∠CBE=55°,则∠DAC的度数为( )
A.70°
B.67.5°
C.62.5°
D.65°
二.填空题(共6小题)
7.如图,在平面直角坐标系中,⊙M经过原点,且与x轴交于点A(﹣4,0),与y轴交于点B(0,2),点C在第二象限⊙M上,且∠AOC=60°,则OC=
.
8.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=72°,则∠BAE=
°.
9.如图,A、D是⊙O上的两点,BC是直径,若∠D=32°,则∠OAC=
度.
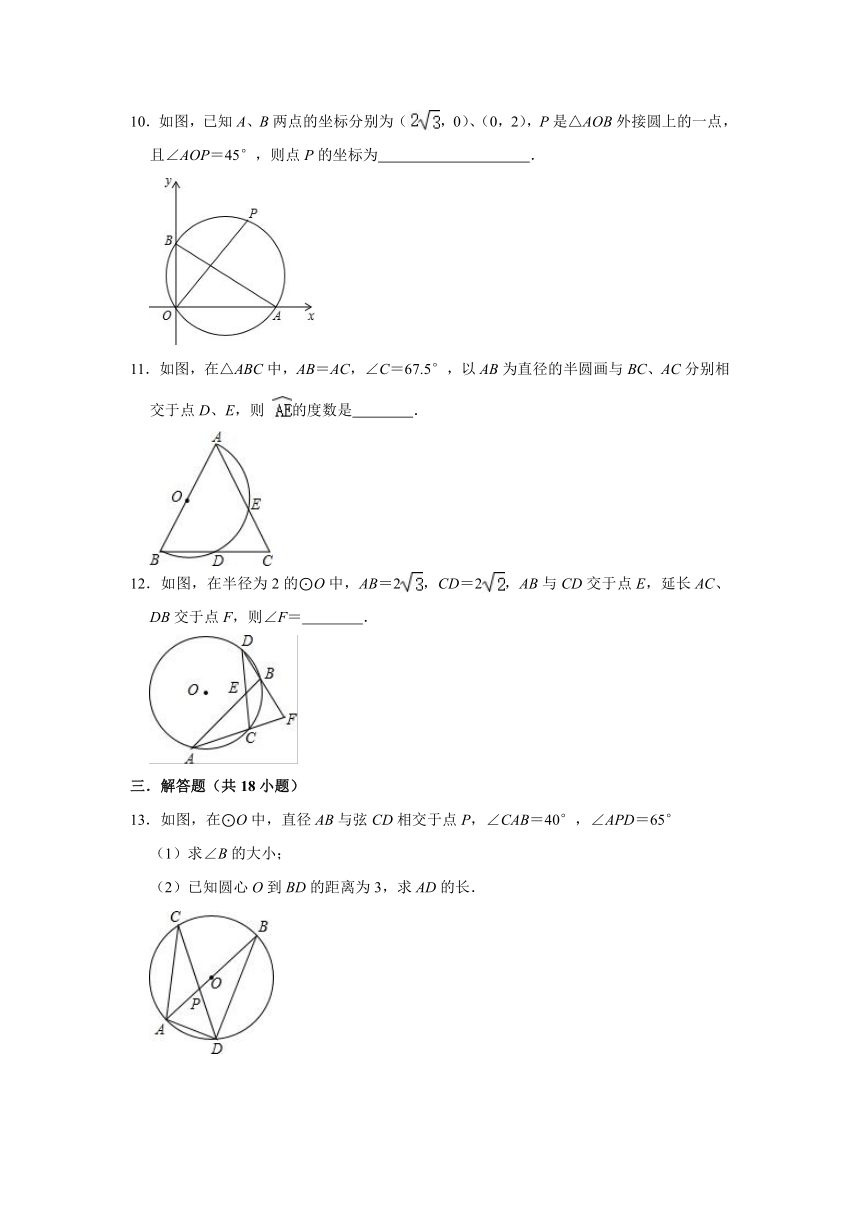
10.如图,已知A、B两点的坐标分别为(,0)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为
.
11.如图,在△ABC中,AB=AC,∠C=67.5°,以AB为直径的半圆画与BC、AC分别相交于点D、E,则
的度数是
.
12.如图,在半径为2的⊙O中,AB=2,CD=2,AB与CD交于点E,延长AC、DB交于点F,则∠F=
.
三.解答题(共18小题)
13.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°
(1)求∠B的大小;
(2)已知圆心O到BD的距离为3,求AD的长.
14.如图,AB是⊙O的直径,点C,D在⊙O上,且=,连接CD,交AB于点E,连接BC,BD.
(1)若∠AOD=130°,求∠BEC的度数;
(2)∠ABD的平分线交CD于点F,求证:BC=CF.
15.如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F.
(1)求证:=;
(2)若CE=1,EB=3,求⊙O的半径;
(3)若BD=6,AB=10,求DE的长.
16.如图,AB是⊙O的直径,P、C是圆周上的点,=,弦PC交AB于点D.
(1)求证:∠A=∠C;
(2)若OD=DC,求∠A的度数.
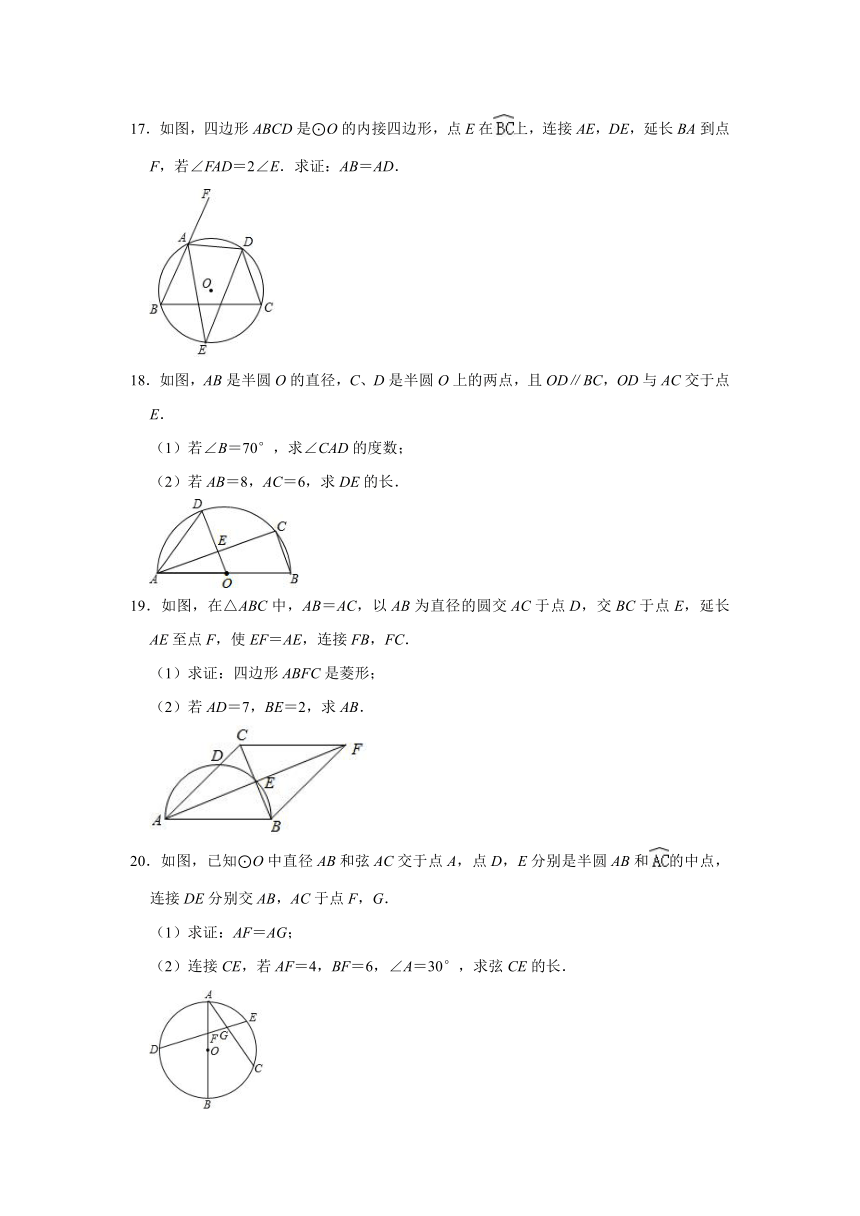
17.如图,四边形ABCD是⊙O的内接四边形,点E在上,连接AE,DE,延长BA到点F,若∠FAD=2∠E.求证:AB=AD.
18.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=8,AC=6,求DE的长.
19.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求AB.
20.如图,已知⊙O中直径AB和弦AC交于点A,点D,E分别是半圆AB和的中点,连接DE分别交AB,AC于点F,G.
(1)求证:AF=AG;
(2)连接CE,若AF=4,BF=6,∠A=30°,求弦CE的长.
21.已知:如图,BC是半⊙O的直径,点D在半圆O上,点A是弧BD的中点.AE⊥BC,垂足为E,BD分别交AE,AC于点F,G.
(1)求证:AF=BF;
(2)点D在何处时,有AG=FG?指出点D的位置并加以证明.
22.如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,AF⊥BC,垂足为D.
(1)求证:∠BAE=∠CAD.
(2)若⊙O的半径为4,AC=5,CD=2,求CF.
23.如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.
(1)求证:AB是⊙O的直径;
(2)延长CB交⊙O于点E,连接DE,求证:DC=DE.
24.如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD的反向延长线与△ABC的外接圆交于点F,连接FB、FC,且FC与AB交于E.
(1)判断△FBC的形状,并说明理由;
(2)请探索线段AB、AC与AF之间满足条件的关系式并说明理由.
25.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC=
°;
(2)求证:∠BAC=2∠DAC;
(3)若AB=10,CD=5,求BC的值.
26.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(1)当∠E=∠F时,则∠ADC=
°;
(2)当∠A=55°,∠E=30°时,求∠F的度数;
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
27.如图,弦AB与CD相交于⊙O内一点P,PC>PD.
(1)试说明:△PAC∽△PDB;
(2)设PA=4,PB=3,CD=8,求PC、PD的长.
28.如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB为⊙O上关于点A、B的滑动角.已知∠APB是⊙O上关于点A、B的滑动角,
(1)若AB为⊙O的直径,则∠APB=
;
(2)若⊙O半径为1,AB=,求∠APB的度数;
(3)若⊙O半径为1,AB=,AC=,求∠BAC的度数.
29.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A,C,D三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)求△ABC外接圆的半径.
30.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
参考答案
一.选择题(共6小题)
1.解:∵OC=OA,
∴∠A=∠OCA=40°,
∴∠BOC=2∠A=80°.
故选:A.
2.解:∵∠ADC+∠B=180°,∠ADC=110°,
∴∠ABC=70°,
∵AB是直径,
∴∠ACB=90°,
∴∠CAB=20°.
故选:A.
3.解:连接OC,如下图所示:
∵∠ADC=125°对应优弧,
∴∠AOC=360°﹣2×125°=110°,
而△AOC为等腰三角形,
∴∠BAC+∠OCA=180°﹣110°=70°,
∴∠BAC=35°,
故A、C、D错误,
故选:B.
4.解:∵∠BAC=120°,AB=AC,
∴∠ACB=30°,
∴∠ACB=∠ADB=30°,
∵BD是⊙O的直径,
∴∠BAD=90°,
∵AB=3,
∴AD=3.
故选:D.
5.解:连接OC,如图所示:
∵OD=OC,
∴∠D=∠OCD,
∵OB∥CD,
∴∠BOC=∠OCD
∴∠BOC=∠D,
∵∠BOC=2∠A,∠A=25°,
∴∠D=2∠A=50°,
∵OB∥CD,
∴∠BOD+∠D=180°,
∴∠BOD=180°﹣50°=130°;
故选:C.
6.解:∵四边形ABCD内接于⊙O,∠CBE=55°,
∴∠ABC=180°﹣∠CBE=180°﹣55°=125°,
∴∠ADC=180°﹣∠ABC=180°﹣125°=55°,
∵AD=DC,
∴∠DAC=∠DCA=(180°﹣∠DAC)=(180°﹣55°)=62.5°,
故选:C.
二.填空题(共6小题)
7.解:连接AC,CM,AB,过点C作CH⊥OA于H,设OC=a.
∵∠AOB=90°,
∴AB是直径,
∵A(﹣4,0),B(0,2),
∴AB===2,
∵∠AMC=2∠AOC=120°,
∴AC=AM=,
在Rt△COH中,OH=OC?cos60°=a,CH=OH=a,
∴AH=4﹣a,
在Rt△ACH中,AC2=AH2+CH2,
∴15=(4﹣a)2+(a)2,
∴a=2+或2﹣(舍弃),
∴OC=2+.
故答案为:2+.
8.解:∵四边形ABCD是平行四边形,∠D=72°,
∴∠DCB=(180°﹣∠D)=108°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=72°,∠B=180°﹣∠BCD=72°
∴∠BAE=180°﹣72°﹣72°=36°,
故答案为:36
9.解:∵∠D=32°,∠D=∠ABC,
∴∠ABC=32°,
∵BC是直径,
∴∠BAC=90°,
∴∠BCA=90°﹣∠ABC=58°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OAC=58°,
故答案为:58.
10.解:∵OB=2,OA=2,
∴AB==4,
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(,1),
可得P点在圆上,P点到圆心的距离为圆的半径2,
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a﹣1,CF=a﹣,PC=2,
∴在Rt△PCF中,利用勾股定理得:(a﹣)2+(a﹣1)2=22,
舍去不合适的根,可得:a=1+,
则P点坐标为(+1,+1).
∵P与P′关于圆心(,1)对称,
∴P′(﹣1,1﹣).
故答案为:(+1,+1)或(﹣1,1﹣)
11.解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
即AD⊥BC,
∵∠C=67.5°,
∴∠ABC=67.5°,
∴∠BAD=22.5°,
∴的度数为45°,
∵AB=AC,AD⊥BC,
∴∠BAD=∠EAD,
∴=,
∴的度数为45°,
∴的度数为180°﹣45°﹣45°=90°.
故答案为:90°.
12.解:作直径CG、AH,交⊙O于G、H,连接AG、DG、BH,
∴∠CDG=∠ABH=90°,
∵AB=2,CD=2,CG=AH=4,
由勾股定理得:DG===2,
BH===2,
∴DG=CD,BH=AH,
∴∠CGD=45°,∠HAB=30°,
∴∠AHB=60°,
∵A、C、D、G四点共圆,
∴∠DCF=∠DGA=∠AGC+∠CGD=∠AGC+45°,
∵∠AHB=∠AGC+∠CDF,∠CDF=∠FAB,
∴∠AHB=∠AGC+∠FAB=60°,
在△DCF中,∠F=180°﹣∠DCF﹣∠CDF,
=180°﹣∠AGC﹣45°﹣∠FAB,
=180°﹣45°﹣60°,
=75°,
故答案为:75°.
三.解答题(共18小题)
13.解:(1)∵∠CAB=∠CDB(同弧所对的圆周角相等),∠CAB=40°,
∴∠CDB=40°,
又∵∠APD=65°,
∴∠BPD=115°,
∴在△BPD中,
∴∠B=180°﹣∠CDB﹣∠BPD=25°;
(2)过点O作OE⊥BD于点E,则OE=3.
∵AB是直径,
∴AD⊥BD(直径所对的圆周角是直角),
∴OE∥AD,
又∵O是AB的中点,
∴OE是△ABD的中位线,
∴AD=2OE=6.
14.解:(1)连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵=,
∴∠A=∠ABC=45°,
∵∠AOD=130°,
∴∠ACD=65°,
∵∠BEC是△ACE的外角,
∴∠BEC=∠A+∠ACD=110°.
(2)证明:∵BF平分∠ABD,
∴∠EBF=∠DBF,
∵,
∴∠ABC=∠CDB,
又∵∠CFB=∠FBD+∠FDB,∠CBF=∠ABC+∠EBF,
∴∠CBF=∠CFB,
∴CF=BC.
15.(1)证明:∵AB是圆的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AFO=∠ADB=90°,
∴OC⊥AD
∴=;
(2)解:连接AC,如图,
∵=,
∴∠CAD=∠ABC,
∵∠ECA=∠ACB,
∴△ACE∽△BCA,
∴AC:CE=CB:AC,
∴AC2=CE?CB,即AC2=1×(1+3),
∴AC=2,
∵AB是圆的直径,
∴∠ACB=90°,
∴AB==2,
∴⊙O的半径为;
(3)解:在Rt△DAB中,AD==8,
∵OC⊥AD,
∴AF=DF=4,
∵OF==3,
∴CF=2,
∵CF∥BD,
∴DE=×4=3.
16.(1)证明:如图,连接OP.
∵=,
∴PA=PC.
在△POA与△POC中,
.
∴△POA≌△POC(SSS).
∴∠A=∠C;
(2)设∠A=∠C=x°,则∠POB=2∠A=2x°.
∵OD=DC,
∴∠DOC=∠C=x°.
在△POC中,x+3x+x=180°
x=36.
∴∠A=36°.
17.证明:连接CA,如图,
∵∠FAD+∠BAD=180°,∠BAD+∠BCD=180°,
∴∠FAD=∠BCD,
∵∠FAD=2∠E,
∴∠BCD=2∠E,
而∠ACD=∠E,
∴∠ACB=∠ACD=∠E,
∴=,
∴AB=AD.
18.解:(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AOD=∠B=70°,
∴∠CAB=90°﹣∠B=90°﹣70°=20°,
∵OA=OD,
∴∠DAO=∠ADO===55°,
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC===2,
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE=BC=.
又∵OD=AB=4,
∴DE=OD﹣OE=4﹣.
19.(1)证明:∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC.
∵AB=AC,
∴BE=CE.
∵AE=EF,
∴四边形ABFC是平行四边形.
又∵AC=AB,
∴四边形ABFC是菱形.
(2)解:设CD=x.连接BD,如图所示.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,
解得:x1=1,x2=﹣8(不合题意,舍去),
∴AB=AC=AD+CD=1+7=8.
20.(1)证明:连接OD,OE,OE交AC于H,如图,
∵点D,E分别是半圆AB和的中点,
∴OD⊥AB,OE⊥AC,
∴∠ODF+∠OFD=90°,∠HEG+∠HGE=90°,
∵∠ODF=∠HEG,
∴∠OFD=∠EGH,
∵∠OFD=∠AFG,∠EGH=∠AGF,
∴∠AFG=∠AGF,
∴AF=AG;
(2)解:方法一:∵AB为直径,AF=4,BF=6,
∴⊙O的半径为5,
在Rt△AOH中,∵∠A=30°,
∴OH=OA=,AH=,
∴HE=5﹣=,
∵OH⊥AC,
∴AH=CH=,
在Rt△CEH中,CE==5.
方法二:连接OC,
∵OA=OC,
∴∠ACO=∠A=30°,
∵∠COH=60°,
∴△OCE为等边三角形,
∴CE=OE=5.
21.(1)证明:连接AB,
∵BC是半⊙O的直径,
∴∠BAC=90°,
∴∠C+∠ABC=90°,
∵AE⊥BC,
∴∠BAE+∠ABE=90°,
∴∠BAE=∠C,
∵点A是弧BD的中点,
∴=,
∴∠ABD=∠C,
∴∠ABD=∠BAE,
∴AF=BF;
(2)解:当=时,有AG=FG,
∴∠C=∠EBF,
∵∠BAC=∠AEC=90°,
∴∠GAF+∠BAE=∠EAC+∠C=90°,
∴∠BAE=∠C,
∴∠EBF=∠BAE,
∵∠AFG=∠BFE,
∴∠AFG+∠FBE=∠BAF+∠FAG=90°,
∴∠AFG=∠GAF,
∴AG=FG.
22.(1)证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠BEA=90°,
∵AF⊥BC,
∴∠ADC=90°,
∴∠ACD+∠CAD=90°,
又∵∠BEA=∠ACD,
∴∠BAE=∠CAD;
(2)解:∵∠ABE=∠ADC=90°,∠BEA=∠ACD,
∴BE=,
由(1)得:∠BAE=∠CAD,
∴,
∴CF=BE=.
23.(1)证明:连接BD,
∵BA=BC,AD=DC,
∴BD⊥AC,
∴∠ADB=90°,
∴AB是⊙O的直径;
(2)证明:∵BA=BC,
∴∠A=∠C,
由圆周角定理得,∠A=∠E,
∴∠C=∠E,
∴DC=DE.
24.解:(1)△FBC为等边三角形.理由如下:
∵∠CAM=120°,AD是∠CAM的平分线,
∴∠CAD=∠MAD=60°;
∴∠FBC=∠CAD=60°,∠FAB=∠MAD=60°;
∴∠FCB=∠FAB=60°,
∴△FBC是等边三角形.
(2)在线段AB上截取AG,使AG=AC,连接CG;
∵∠GAC=∠BFC=60°,
∴△AGC为等边三角形,AC=GC;∠ACG=60°;
∵∠BCF=60°,
∴∠ACF=∠GCB;在△ACF与△GCB中,
,
∴△ACF≌△GCB(SAS),
∴AF=BG,
∴AB=AC+AF.
25.(1)解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠ACB=70°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC=180°﹣∠BAC=110°,
故答案为:110;
(2)证明:∵BD⊥AC,
∴∠AEB=∠BEC=90°,
∴∠ACB=90°﹣∠CBD,
∵AB=AC,
∴∠ABC=∠ACB=90°﹣∠CBD,
∴∠BAC=180°﹣2∠ABC=2∠CBD,
∵∠DAC=∠CBD,
∴∠BAC=2∠DAC;
(3)解:过A作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH=CAB,CH=BH,
∵∠BAC=2∠DAC,
∴∠CAG=∠CAH,
过C作CG⊥AD交AD的延长线于G,
∴∠G=∠AHC=90°,
∵AC=AC,
∴△AGC≌△AHC(AAS),
∴AG=AH,CG=CH,
∵∠CDG=∠ABC,
设BH=k,AH=2k,
∴AB==k=10,
∴k=2,
∴BC=2k=4.
26.解:(1)∵∠E=∠F,∠DCE=∠BCF,∠ADC=∠E+∠DCE,∠ABC=∠BCF+∠F,
∴∠ADC=∠ABC,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ADC=90°.
故答案为:90°;
(2)∵在△ABE中,∠A=55°,∠E=30°,
∴∠ABE=180°﹣∠A﹣∠E=95°,
∴∠ADF=180°﹣∠ABE=85°,
∴在△ADF中,∠F=180°﹣∠ADF﹣∠A=40°;
(3)∵∠ADC=180°﹣∠A﹣∠F,∠ABC=180°﹣∠A﹣∠E,
∵∠ADC+∠ABC=180°,
∴180°﹣∠A﹣∠F+180°﹣∠A﹣∠E=180°,
∴2∠A+∠E+∠F=180°,
∴∠A=90°﹣=90°﹣.
27.(1)证明:由圆周角定理得,∠A=∠D,∠C=∠B,
∴△PAC∽△PDB;
(2)解:由相交弦定理得到,PA?PB=PC?PD,即3×4=PC×(8﹣PC),
解得,PC=2或6,
则PD=6或2,
∵PC>PD,
∴PC=6,PD=2.
28.解:(1)∵AB为⊙O的直径,
∴∠APB=90°.
故答案为:90°;
(2)连接OA,OB,AB,
∵⊙O半径为1,AB=,
∴OA=OB=1,AB=,
∴OA2+OB2=AB2,
∴∠AOB=90°,
∴当点P在优弧AB上时,∠APB=∠AOB=45°,
当点P在劣弧AB上时,∠APB=180°﹣45°=135°,
∴∠APB的度数为:45°或135°;
(3)解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE=AC=,AD=AB=,
∴∠AOE=60°,∠AOD=45°,
∴∠BAO=45°,∠CAO=90°﹣60°=30°,
∴∠BAC=45°+30°=75°,或∠BAC′=45°﹣30°=15°.
∴∠BAC=15°或75°.
29.(1)证明:∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),
∴AD为圆O的直径(90°的圆周角所对的弦为圆的直径),
∴∠AED=90°(直径所对的圆周角为直角),
又∵AD是△ABC的∠BAC的平分线(已知),
∴∠CAD=∠EAD(角平分线定义),
∴CD=DE(在同圆或等圆中,相等的圆周角所对的弦相等),
在Rt△ACD和Rt△AED中,,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE(全等三角形的对应边相等);
(2)解:∵在Rt△ABC中,∠ACB=90°,AC=5,CB=12,
∴AB===13,
∴△ABC外接圆的半径=AB=×13=.
30.(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,
在Rt△ABC中,AC2+BC2=AB2,
∴(x﹣2)2+x2=42,
解得:x1=1+,x2=1﹣(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=1+.
一.选择题(共6小题)
1.如图,AB是⊙O的直径,点C在⊙O上,∠OCA=40°,则∠BOC的度数为( )
A.80°
B.90°
C.100°
D.50°
2.如图,AB是⊙O的直径,点C,D在⊙O上,若∠D=110°,则∠BAC的度数为( )
A.20°
B.35°
C.55°
D.90°
3.如图,AB是半圆的直径,C、D是半圆上的两点,若∠ADC=125°,则∠BAC的度数是( )
A.25°
B.35°
C.45°
D.55°
4.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AB=3,则AD的值为( )
A.6
B.
C.5
D.
5.如图,点A、B、C、D在⊙O上,OB∥CD,∠A=25°,则∠BOD等于( )
A.100°
B.120°
C.130°
D.150°
6.如图,四边形ABCD内接于⊙O,DA=DC,若∠CBE=55°,则∠DAC的度数为( )
A.70°
B.67.5°
C.62.5°
D.65°
二.填空题(共6小题)
7.如图,在平面直角坐标系中,⊙M经过原点,且与x轴交于点A(﹣4,0),与y轴交于点B(0,2),点C在第二象限⊙M上,且∠AOC=60°,则OC=
.
8.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=72°,则∠BAE=
°.
9.如图,A、D是⊙O上的两点,BC是直径,若∠D=32°,则∠OAC=
度.
10.如图,已知A、B两点的坐标分别为(,0)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为
.
11.如图,在△ABC中,AB=AC,∠C=67.5°,以AB为直径的半圆画与BC、AC分别相交于点D、E,则
的度数是
.
12.如图,在半径为2的⊙O中,AB=2,CD=2,AB与CD交于点E,延长AC、DB交于点F,则∠F=
.
三.解答题(共18小题)
13.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°
(1)求∠B的大小;
(2)已知圆心O到BD的距离为3,求AD的长.
14.如图,AB是⊙O的直径,点C,D在⊙O上,且=,连接CD,交AB于点E,连接BC,BD.
(1)若∠AOD=130°,求∠BEC的度数;
(2)∠ABD的平分线交CD于点F,求证:BC=CF.
15.如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F.
(1)求证:=;
(2)若CE=1,EB=3,求⊙O的半径;
(3)若BD=6,AB=10,求DE的长.
16.如图,AB是⊙O的直径,P、C是圆周上的点,=,弦PC交AB于点D.
(1)求证:∠A=∠C;
(2)若OD=DC,求∠A的度数.
17.如图,四边形ABCD是⊙O的内接四边形,点E在上,连接AE,DE,延长BA到点F,若∠FAD=2∠E.求证:AB=AD.
18.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=8,AC=6,求DE的长.
19.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求AB.
20.如图,已知⊙O中直径AB和弦AC交于点A,点D,E分别是半圆AB和的中点,连接DE分别交AB,AC于点F,G.
(1)求证:AF=AG;
(2)连接CE,若AF=4,BF=6,∠A=30°,求弦CE的长.
21.已知:如图,BC是半⊙O的直径,点D在半圆O上,点A是弧BD的中点.AE⊥BC,垂足为E,BD分别交AE,AC于点F,G.
(1)求证:AF=BF;
(2)点D在何处时,有AG=FG?指出点D的位置并加以证明.
22.如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,AF⊥BC,垂足为D.
(1)求证:∠BAE=∠CAD.
(2)若⊙O的半径为4,AC=5,CD=2,求CF.
23.如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.
(1)求证:AB是⊙O的直径;
(2)延长CB交⊙O于点E,连接DE,求证:DC=DE.
24.如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD的反向延长线与△ABC的外接圆交于点F,连接FB、FC,且FC与AB交于E.
(1)判断△FBC的形状,并说明理由;
(2)请探索线段AB、AC与AF之间满足条件的关系式并说明理由.
25.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC=
°;
(2)求证:∠BAC=2∠DAC;
(3)若AB=10,CD=5,求BC的值.
26.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(1)当∠E=∠F时,则∠ADC=
°;
(2)当∠A=55°,∠E=30°时,求∠F的度数;
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
27.如图,弦AB与CD相交于⊙O内一点P,PC>PD.
(1)试说明:△PAC∽△PDB;
(2)设PA=4,PB=3,CD=8,求PC、PD的长.
28.如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB为⊙O上关于点A、B的滑动角.已知∠APB是⊙O上关于点A、B的滑动角,
(1)若AB为⊙O的直径,则∠APB=
;
(2)若⊙O半径为1,AB=,求∠APB的度数;
(3)若⊙O半径为1,AB=,AC=,求∠BAC的度数.
29.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A,C,D三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)求△ABC外接圆的半径.
30.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
参考答案
一.选择题(共6小题)
1.解:∵OC=OA,
∴∠A=∠OCA=40°,
∴∠BOC=2∠A=80°.
故选:A.
2.解:∵∠ADC+∠B=180°,∠ADC=110°,
∴∠ABC=70°,
∵AB是直径,
∴∠ACB=90°,
∴∠CAB=20°.
故选:A.
3.解:连接OC,如下图所示:
∵∠ADC=125°对应优弧,
∴∠AOC=360°﹣2×125°=110°,
而△AOC为等腰三角形,
∴∠BAC+∠OCA=180°﹣110°=70°,
∴∠BAC=35°,
故A、C、D错误,
故选:B.
4.解:∵∠BAC=120°,AB=AC,
∴∠ACB=30°,
∴∠ACB=∠ADB=30°,
∵BD是⊙O的直径,
∴∠BAD=90°,
∵AB=3,
∴AD=3.
故选:D.
5.解:连接OC,如图所示:
∵OD=OC,
∴∠D=∠OCD,
∵OB∥CD,
∴∠BOC=∠OCD
∴∠BOC=∠D,
∵∠BOC=2∠A,∠A=25°,
∴∠D=2∠A=50°,
∵OB∥CD,
∴∠BOD+∠D=180°,
∴∠BOD=180°﹣50°=130°;
故选:C.
6.解:∵四边形ABCD内接于⊙O,∠CBE=55°,
∴∠ABC=180°﹣∠CBE=180°﹣55°=125°,
∴∠ADC=180°﹣∠ABC=180°﹣125°=55°,
∵AD=DC,
∴∠DAC=∠DCA=(180°﹣∠DAC)=(180°﹣55°)=62.5°,
故选:C.
二.填空题(共6小题)
7.解:连接AC,CM,AB,过点C作CH⊥OA于H,设OC=a.
∵∠AOB=90°,
∴AB是直径,
∵A(﹣4,0),B(0,2),
∴AB===2,
∵∠AMC=2∠AOC=120°,
∴AC=AM=,
在Rt△COH中,OH=OC?cos60°=a,CH=OH=a,
∴AH=4﹣a,
在Rt△ACH中,AC2=AH2+CH2,
∴15=(4﹣a)2+(a)2,
∴a=2+或2﹣(舍弃),
∴OC=2+.
故答案为:2+.
8.解:∵四边形ABCD是平行四边形,∠D=72°,
∴∠DCB=(180°﹣∠D)=108°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=72°,∠B=180°﹣∠BCD=72°
∴∠BAE=180°﹣72°﹣72°=36°,
故答案为:36
9.解:∵∠D=32°,∠D=∠ABC,
∴∠ABC=32°,
∵BC是直径,
∴∠BAC=90°,
∴∠BCA=90°﹣∠ABC=58°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OAC=58°,
故答案为:58.
10.解:∵OB=2,OA=2,
∴AB==4,
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(,1),
可得P点在圆上,P点到圆心的距离为圆的半径2,
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a﹣1,CF=a﹣,PC=2,
∴在Rt△PCF中,利用勾股定理得:(a﹣)2+(a﹣1)2=22,
舍去不合适的根,可得:a=1+,
则P点坐标为(+1,+1).
∵P与P′关于圆心(,1)对称,
∴P′(﹣1,1﹣).
故答案为:(+1,+1)或(﹣1,1﹣)
11.解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
即AD⊥BC,
∵∠C=67.5°,
∴∠ABC=67.5°,
∴∠BAD=22.5°,
∴的度数为45°,
∵AB=AC,AD⊥BC,
∴∠BAD=∠EAD,
∴=,
∴的度数为45°,
∴的度数为180°﹣45°﹣45°=90°.
故答案为:90°.
12.解:作直径CG、AH,交⊙O于G、H,连接AG、DG、BH,
∴∠CDG=∠ABH=90°,
∵AB=2,CD=2,CG=AH=4,
由勾股定理得:DG===2,
BH===2,
∴DG=CD,BH=AH,
∴∠CGD=45°,∠HAB=30°,
∴∠AHB=60°,
∵A、C、D、G四点共圆,
∴∠DCF=∠DGA=∠AGC+∠CGD=∠AGC+45°,
∵∠AHB=∠AGC+∠CDF,∠CDF=∠FAB,
∴∠AHB=∠AGC+∠FAB=60°,
在△DCF中,∠F=180°﹣∠DCF﹣∠CDF,
=180°﹣∠AGC﹣45°﹣∠FAB,
=180°﹣45°﹣60°,
=75°,
故答案为:75°.
三.解答题(共18小题)
13.解:(1)∵∠CAB=∠CDB(同弧所对的圆周角相等),∠CAB=40°,
∴∠CDB=40°,
又∵∠APD=65°,
∴∠BPD=115°,
∴在△BPD中,
∴∠B=180°﹣∠CDB﹣∠BPD=25°;
(2)过点O作OE⊥BD于点E,则OE=3.
∵AB是直径,
∴AD⊥BD(直径所对的圆周角是直角),
∴OE∥AD,
又∵O是AB的中点,
∴OE是△ABD的中位线,
∴AD=2OE=6.
14.解:(1)连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵=,
∴∠A=∠ABC=45°,
∵∠AOD=130°,
∴∠ACD=65°,
∵∠BEC是△ACE的外角,
∴∠BEC=∠A+∠ACD=110°.
(2)证明:∵BF平分∠ABD,
∴∠EBF=∠DBF,
∵,
∴∠ABC=∠CDB,
又∵∠CFB=∠FBD+∠FDB,∠CBF=∠ABC+∠EBF,
∴∠CBF=∠CFB,
∴CF=BC.
15.(1)证明:∵AB是圆的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AFO=∠ADB=90°,
∴OC⊥AD
∴=;
(2)解:连接AC,如图,
∵=,
∴∠CAD=∠ABC,
∵∠ECA=∠ACB,
∴△ACE∽△BCA,
∴AC:CE=CB:AC,
∴AC2=CE?CB,即AC2=1×(1+3),
∴AC=2,
∵AB是圆的直径,
∴∠ACB=90°,
∴AB==2,
∴⊙O的半径为;
(3)解:在Rt△DAB中,AD==8,
∵OC⊥AD,
∴AF=DF=4,
∵OF==3,
∴CF=2,
∵CF∥BD,
∴DE=×4=3.
16.(1)证明:如图,连接OP.
∵=,
∴PA=PC.
在△POA与△POC中,
.
∴△POA≌△POC(SSS).
∴∠A=∠C;
(2)设∠A=∠C=x°,则∠POB=2∠A=2x°.
∵OD=DC,
∴∠DOC=∠C=x°.
在△POC中,x+3x+x=180°
x=36.
∴∠A=36°.
17.证明:连接CA,如图,
∵∠FAD+∠BAD=180°,∠BAD+∠BCD=180°,
∴∠FAD=∠BCD,
∵∠FAD=2∠E,
∴∠BCD=2∠E,
而∠ACD=∠E,
∴∠ACB=∠ACD=∠E,
∴=,
∴AB=AD.
18.解:(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AOD=∠B=70°,
∴∠CAB=90°﹣∠B=90°﹣70°=20°,
∵OA=OD,
∴∠DAO=∠ADO===55°,
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC===2,
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE=BC=.
又∵OD=AB=4,
∴DE=OD﹣OE=4﹣.
19.(1)证明:∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC.
∵AB=AC,
∴BE=CE.
∵AE=EF,
∴四边形ABFC是平行四边形.
又∵AC=AB,
∴四边形ABFC是菱形.
(2)解:设CD=x.连接BD,如图所示.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,
解得:x1=1,x2=﹣8(不合题意,舍去),
∴AB=AC=AD+CD=1+7=8.
20.(1)证明:连接OD,OE,OE交AC于H,如图,
∵点D,E分别是半圆AB和的中点,
∴OD⊥AB,OE⊥AC,
∴∠ODF+∠OFD=90°,∠HEG+∠HGE=90°,
∵∠ODF=∠HEG,
∴∠OFD=∠EGH,
∵∠OFD=∠AFG,∠EGH=∠AGF,
∴∠AFG=∠AGF,
∴AF=AG;
(2)解:方法一:∵AB为直径,AF=4,BF=6,
∴⊙O的半径为5,
在Rt△AOH中,∵∠A=30°,
∴OH=OA=,AH=,
∴HE=5﹣=,
∵OH⊥AC,
∴AH=CH=,
在Rt△CEH中,CE==5.
方法二:连接OC,
∵OA=OC,
∴∠ACO=∠A=30°,
∵∠COH=60°,
∴△OCE为等边三角形,
∴CE=OE=5.
21.(1)证明:连接AB,
∵BC是半⊙O的直径,
∴∠BAC=90°,
∴∠C+∠ABC=90°,
∵AE⊥BC,
∴∠BAE+∠ABE=90°,
∴∠BAE=∠C,
∵点A是弧BD的中点,
∴=,
∴∠ABD=∠C,
∴∠ABD=∠BAE,
∴AF=BF;
(2)解:当=时,有AG=FG,
∴∠C=∠EBF,
∵∠BAC=∠AEC=90°,
∴∠GAF+∠BAE=∠EAC+∠C=90°,
∴∠BAE=∠C,
∴∠EBF=∠BAE,
∵∠AFG=∠BFE,
∴∠AFG+∠FBE=∠BAF+∠FAG=90°,
∴∠AFG=∠GAF,
∴AG=FG.
22.(1)证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠BEA=90°,
∵AF⊥BC,
∴∠ADC=90°,
∴∠ACD+∠CAD=90°,
又∵∠BEA=∠ACD,
∴∠BAE=∠CAD;
(2)解:∵∠ABE=∠ADC=90°,∠BEA=∠ACD,
∴BE=,
由(1)得:∠BAE=∠CAD,
∴,
∴CF=BE=.
23.(1)证明:连接BD,
∵BA=BC,AD=DC,
∴BD⊥AC,
∴∠ADB=90°,
∴AB是⊙O的直径;
(2)证明:∵BA=BC,
∴∠A=∠C,
由圆周角定理得,∠A=∠E,
∴∠C=∠E,
∴DC=DE.
24.解:(1)△FBC为等边三角形.理由如下:
∵∠CAM=120°,AD是∠CAM的平分线,
∴∠CAD=∠MAD=60°;
∴∠FBC=∠CAD=60°,∠FAB=∠MAD=60°;
∴∠FCB=∠FAB=60°,
∴△FBC是等边三角形.
(2)在线段AB上截取AG,使AG=AC,连接CG;
∵∠GAC=∠BFC=60°,
∴△AGC为等边三角形,AC=GC;∠ACG=60°;
∵∠BCF=60°,
∴∠ACF=∠GCB;在△ACF与△GCB中,
,
∴△ACF≌△GCB(SAS),
∴AF=BG,
∴AB=AC+AF.
25.(1)解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠ACB=70°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC=180°﹣∠BAC=110°,
故答案为:110;
(2)证明:∵BD⊥AC,
∴∠AEB=∠BEC=90°,
∴∠ACB=90°﹣∠CBD,
∵AB=AC,
∴∠ABC=∠ACB=90°﹣∠CBD,
∴∠BAC=180°﹣2∠ABC=2∠CBD,
∵∠DAC=∠CBD,
∴∠BAC=2∠DAC;
(3)解:过A作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH=CAB,CH=BH,
∵∠BAC=2∠DAC,
∴∠CAG=∠CAH,
过C作CG⊥AD交AD的延长线于G,
∴∠G=∠AHC=90°,
∵AC=AC,
∴△AGC≌△AHC(AAS),
∴AG=AH,CG=CH,
∵∠CDG=∠ABC,
设BH=k,AH=2k,
∴AB==k=10,
∴k=2,
∴BC=2k=4.
26.解:(1)∵∠E=∠F,∠DCE=∠BCF,∠ADC=∠E+∠DCE,∠ABC=∠BCF+∠F,
∴∠ADC=∠ABC,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ADC=90°.
故答案为:90°;
(2)∵在△ABE中,∠A=55°,∠E=30°,
∴∠ABE=180°﹣∠A﹣∠E=95°,
∴∠ADF=180°﹣∠ABE=85°,
∴在△ADF中,∠F=180°﹣∠ADF﹣∠A=40°;
(3)∵∠ADC=180°﹣∠A﹣∠F,∠ABC=180°﹣∠A﹣∠E,
∵∠ADC+∠ABC=180°,
∴180°﹣∠A﹣∠F+180°﹣∠A﹣∠E=180°,
∴2∠A+∠E+∠F=180°,
∴∠A=90°﹣=90°﹣.
27.(1)证明:由圆周角定理得,∠A=∠D,∠C=∠B,
∴△PAC∽△PDB;
(2)解:由相交弦定理得到,PA?PB=PC?PD,即3×4=PC×(8﹣PC),
解得,PC=2或6,
则PD=6或2,
∵PC>PD,
∴PC=6,PD=2.
28.解:(1)∵AB为⊙O的直径,
∴∠APB=90°.
故答案为:90°;
(2)连接OA,OB,AB,
∵⊙O半径为1,AB=,
∴OA=OB=1,AB=,
∴OA2+OB2=AB2,
∴∠AOB=90°,
∴当点P在优弧AB上时,∠APB=∠AOB=45°,
当点P在劣弧AB上时,∠APB=180°﹣45°=135°,
∴∠APB的度数为:45°或135°;
(3)解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE=AC=,AD=AB=,
∴∠AOE=60°,∠AOD=45°,
∴∠BAO=45°,∠CAO=90°﹣60°=30°,
∴∠BAC=45°+30°=75°,或∠BAC′=45°﹣30°=15°.
∴∠BAC=15°或75°.
29.(1)证明:∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),
∴AD为圆O的直径(90°的圆周角所对的弦为圆的直径),
∴∠AED=90°(直径所对的圆周角为直角),
又∵AD是△ABC的∠BAC的平分线(已知),
∴∠CAD=∠EAD(角平分线定义),
∴CD=DE(在同圆或等圆中,相等的圆周角所对的弦相等),
在Rt△ACD和Rt△AED中,,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE(全等三角形的对应边相等);
(2)解:∵在Rt△ABC中,∠ACB=90°,AC=5,CB=12,
∴AB===13,
∴△ABC外接圆的半径=AB=×13=.
30.(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,
在Rt△ABC中,AC2+BC2=AB2,
∴(x﹣2)2+x2=42,
解得:x1=1+,x2=1﹣(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=1+.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
