《2.5直线与圆的位置关系》同步能力提升训练2021-2022学年苏科版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 《2.5直线与圆的位置关系》同步能力提升训练2021-2022学年苏科版九年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 356.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 21:14:46 | ||
图片预览




文档简介
2021年苏科版九年级数学上册《2.5直线与圆的位置关系》同步能力提升训练(附答案)
一、选择题
1.如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4
B.8
C.4或6
D.4或8
2.如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是( )
A.50°
B.55°
C.60°
D.65°
3.如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )
A.
B.
C.
D.
4.如图,两同心圆间的圆环的面积为16π,过小圆上任意一点P作大圆的弦AB,则PA?PB的值是( )
A.16
B.16π
C.4
D.4π
5.如图,⊙I为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE与⊙I相切,DE∥BC,则DE的长( )
A.3.6
B.
C.3
D.
6.已知三角形的周长为12,面积为6,则该三角形内切圆的半径为( )
A.4
B.3
C.2
D.1
7.如图,点A的坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
A.(﹣4,0)
B.(﹣2,0)
C.(﹣4,0)或(﹣2,0)
D.(﹣3,0)
8.如图,AB是⊙O的直径,点C为⊙O上一点,过点C作⊙O的切线,交直径AB的延长于点D,若∠ABC=65°,则∠D的度数是( )
A.25°
B.30°
C.40°
D.50°
9.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD=6,则CB长( )
A.4
B.5
C.6
D.无法确定
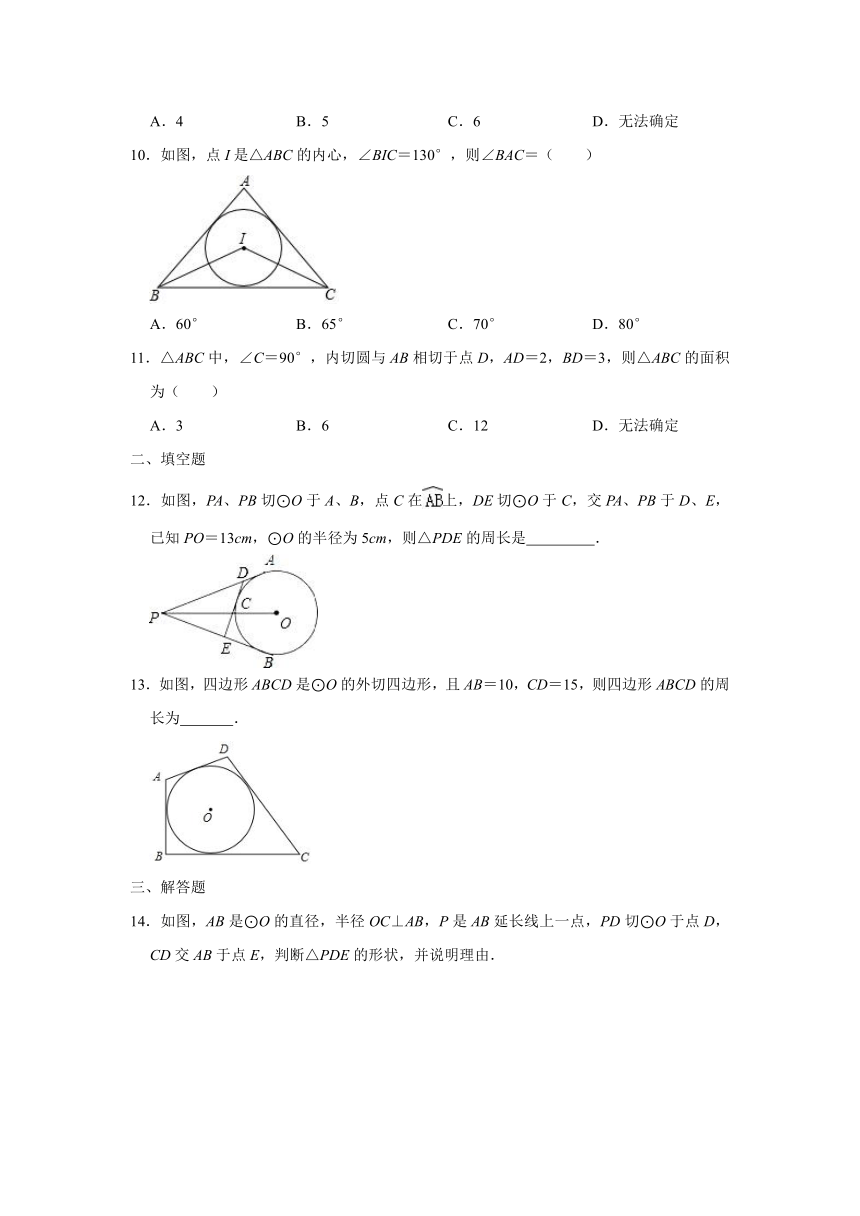
10.如图,点I是△ABC的内心,∠BIC=130°,则∠BAC=( )
A.60°
B.65°
C.70°
D.80°
11.△ABC中,∠C=90°,内切圆与AB相切于点D,AD=2,BD=3,则△ABC的面积为( )
A.3
B.6
C.12
D.无法确定
二、填空题
12.如图,PA、PB切⊙O于A、B,点C在上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是
.
13.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为
.
三、解答题
14.如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.
15.已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,
(1)求证:DE是⊙O的切线.
(2)当BC=10,AD=4时,求⊙O的半径.
16.如图,已知△ABC内接于⊙O,过点B作直线EF∥AC,又知∠ACB=∠BDC=60°,AC=cm.
(1)请探究EF与⊙O的位置关系,并说明理由;
(2)求⊙O的周长.
17.如图,已知AB是⊙O的直径,∠DAC=∠B,判断AD与⊙O的位置关系,并说明理由.
18.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)如图1,证明:OD∥BC;
(2)如图2,若AD是⊙O的切线,连接BD交于⊙O于点F,连接EF,且OA=,求EF的长.
19.如图,⊙O的直径BE为4,∠BAE的平分线AD交⊙O于点D,交BE于点F,C是BE延长线上一点,且FC=AC.
(1)求BD的长;
(2)求证:AC是⊙O的切线.
20.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB
(1)求证:DC为⊙O的切线;
(2)若∠DAB=60°,⊙O的半径为3,求线段AC的长
21.如图,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC中点,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)设CD与OE的交点为F,若AB=10,BC=6,求OF的长.
参考答案
1.解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒)
∴⊙P与直线CD相切时,时间为4秒,
当点P在点O的右侧时,同法可得t=8秒
故选:D.
2.
解:连接BC,
∵DB、DE分别切⊙O于点B、C,
∴BD=DC,
∵∠ACE=25°,
∴∠ABC=25°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠DBC=∠DCB=90°﹣25°=65°,
∴∠D=50°.
故选:A.
3.解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,
∴AC=EC,DE=DB,PA=PB
∵△PCD的周长等于3,
∴PA+PB=3,
∴PA=.
故选:A.
4.解:过P点作大圆的直径CD,如图,设大圆半径为R,小圆半径为r,
∵PA?PB=PC?PD,
∴PA?PB=(OC﹣OP)?(OP+OD)
=(R﹣r)(R+r)
=R2﹣r2,
∵两同心圆间的圆环(即图中阴影部分)的面积为16π,
∴πR2﹣πr2=16π,
∴R2﹣r2=16,
∴PA?PB=16.
故选:A.
5.解:如图,⊙I与AB、AC、DE的切点为M、N、G,设DG=DM=x,EG=EN=y.
∵AM=AN==,
∴AD=﹣x,AE=﹣y,
∵DE∥BC,
∴x=,y=,
∴DE=x+y=+=.故选:B.
6.解:设这个三角形的内切圆半径是r,
∵三角形周长为12,面积为6,
∴×12r=6,
解得r=1.
故选:D.
7.解:连接AQ,AP.
根据切线的性质定理,得AQ⊥PQ;
要使PQ最小,只需AP最小,
根据垂线段最短,可知当AP⊥x轴时,AP最短,
∴P点的坐标是(﹣3,0).
故选:D.
8.解:连接OC,如图,
∵CD为切线,
∴OC⊥CD,
∴∠OCD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=90°﹣∠ABC=90°﹣65°=25°,
∴∠BCD=∠A=25°,
∵∠OBC=∠BCD+∠D
∴∠D=65°﹣25°=40°.
故选:C.
9.解:方法1、
设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH.
设CD=y,CB=x.
设S梯形ABCD=S
则S=(CD+AB)R=(y+10)R
S=S△BOC+S△COD+S△DOA
=xR+yR+×6R
联立(1)(2)得x=4;
方法2、连接OD.OC
∵AD,CD是⊙O的切线,
∴∠ADO=∠ODC,
∵CD∥AB,
∴∠ODC=∠AOD,
∴∠ADO=∠AOD
∴AD=OA
∵AD=6,
∴OA=6,
∵AB=10,
∴OB=4,
同理可得
OB=BC=4,
故选:A.
10.解:∵点I是△ABC的内心,
∴∠ABC=2∠IBC,∠ACB=2∠ICB,
∵∠BIC=130°,
∴∠IBC+∠ICB=180°﹣∠CIB=50°,
∴∠ABC+∠ACB=2×50°=100°,
∴∠BAC=180°﹣(∠ACB+∠ABC)=80°.
故选:D.
11.解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.
根据切线长定理,得AE=AD=2,BF=BD=3,CF=CE=x.
根据勾股定理,得(x+2)2+(x+3)2=(2+3)2.
整理,得x2+5x=6.
所以S△ABC=AC?BC
=(x+2)(x+3)
=(x2+5x+6)
=×(6+6)
=6.
故选:B.
12.解:连接OA、OB,如下图所示:
∵PA、PB为圆的两条切线,
∴由切线长定理可得:PA=PB,
同理可知:DA=DC,EC=EB;
∵OA⊥PA,OA=5,PO=13,
∴由勾股定理得:PA=12,
∴PA=PB=12;
∵△PDE的周长=PD+DC+CE+PE,DA=DC,EC=EB;
∴△PDE的周长=PD+DA+PE+EB=PA+PB=24,
故此题应该填24cm.
13.解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=25,
∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50,
故答案为:50.
14.解:△PDE是等腰三角形.
理由是:连接OD,
∵OC⊥AB,
∴∠CEO+∠OCE=90°,
∵OC=OD,
∴∠OCE=∠ODE,
∵PD切⊙O,
∴∠ODE+∠PDE=90°,
∵∠OEC=∠PED,
∴∠PDE=∠PED,
∴PD=PE,
∴△PDE是等腰三角形.
15.(1)证明:连接OE、OD,
在△AOD和△EOD中,
,
∴△AOD≌△EOD(SSS),
∴∠OED=∠BAC=90°,
∴DE是⊙O的切线;
(2)解:∵△AOD≌△EOD,
∴∠AOD=∠EOD,
∵OB=OE,
∴∠B=∠OEB,
∵∠AOE=∠B+∠OEB,
∴∠BEO=∠EOD,
∴OD∥BC,又AO=BO,
∴OD=BC=5,
由勾股定理得,AO==3,
则⊙O的半径为3.
16.解:(1)EF与⊙O相切.理由如下:
延长BO交AC于H,如图,
∵∠BAC=∠BDC=60°,
而∠ACB=60°,
∴△ABC为等边三角形,
∵点O为△ABC的外心,
∴BH⊥AC,
∵AC∥EF,
∴BH⊥EF,
∴EF为⊙O的切线;
(2)连接OA,如图,
∵△ABC为等边三角形,
∴OA平分∠ABC,
∴∠OAH=30°,
∵OH⊥AC,
∴AH=CH=AC=,
∴OA=1,
∴⊙O的周长=2π×1=2π(cm).
17.解:直线AD是⊙O的切线
∵AB是⊙O的直径
∴∠ACB=90°
∴∠B+∠BAC=90°
∵∠DAC=∠B,
∴∠DAC+∠BAC=90°
∴AB⊥AD,且AB是直径
∴AD是⊙O的切线
18.解:(1)连接OC,
在△OAD和△OCD中,
,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∴OD∥BC;
(2)连接AF,过F作FM⊥EF交OD于M,
∵AB=AD,AD是圆的切线,
∴△ABD为等腰直角三角形,
∵AB为直径,
∴∠AFB=90°,∠DAF=45°,
∵∠AED=∠AFD=90°,
∴∠DAF=∠ADF=45°,∠EAF=∠FDM,
∴AF=DF,
∵∠EFM=∠AFD=90°,
∴∠AFE=∠DFM,
∴△AEF≌△DMF(ASA),
∴AE=DM,
∵,OA=,
∴OD==5,
∴AE=DM==2,DE=4,
∴EM=4﹣2=2,
∴EF=.
19.(1)解:如图1,连接OD.
∵BE为⊙O的直径,
∴∠BAE=90°.
∵AD平分∠BAE,∠BAD=∠EAD=45°.
∴∠BOD=2∠BAD=90°.
∴Rt△BOD中,.
(2)证明:如图,连接OA.
∵AC=FC,
∴∠FAC=∠CFA.
∵∠DFO=∠CFA,
∴∠DFO=∠FAC.
∵OA=OD,
∴∠OAF=∠ODF.
由(1)知∠BOD=90°,
∴∠DFO+∠ODF=∠CAF+∠OAF=90°.
∴OA⊥AC于A,
∴AC是⊙O的切线.
20.(1)证明:连接CO,
∵AO=CO,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠OAC=∠DAC,
∴∠DAC=∠OCA,
∴CO∥AD,AD⊥CD,
∴CO⊥CD,
∴DC为⊙O的切线;
(2)连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠DAB=60°,AC平分∠DAB,
∴∠BAC=∠DAB=30°,
∵⊙O的半径为3,
∴AB=6,
∴AC=AB=3.
21.解:(1)DE与⊙O相切.
理由如下:连接CD、OD,如图,
∵BC为直径,
∴∠BDC=90°,
∵E为Rt△ADC的斜边AC的中点,
∴EA=ED,
∴∠1=∠A,
∵OB=OD,
∴∠B=∠2,
而∠B+∠A=90°
∴∠1+∠2=90°,
∴∠EDO=90°,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)∵∠DBC=∠CBA,∠BDC=∠BCA,
∴BD=,
∵OB=OC,EC=EA,
∴OE为△CAB的中位线,
∴OF∥BD,
∴OF:BD=OC:CB,
∴OF=BD=.
一、选择题
1.如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4
B.8
C.4或6
D.4或8
2.如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是( )
A.50°
B.55°
C.60°
D.65°
3.如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )
A.
B.
C.
D.
4.如图,两同心圆间的圆环的面积为16π,过小圆上任意一点P作大圆的弦AB,则PA?PB的值是( )
A.16
B.16π
C.4
D.4π
5.如图,⊙I为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE与⊙I相切,DE∥BC,则DE的长( )
A.3.6
B.
C.3
D.
6.已知三角形的周长为12,面积为6,则该三角形内切圆的半径为( )
A.4
B.3
C.2
D.1
7.如图,点A的坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
A.(﹣4,0)
B.(﹣2,0)
C.(﹣4,0)或(﹣2,0)
D.(﹣3,0)
8.如图,AB是⊙O的直径,点C为⊙O上一点,过点C作⊙O的切线,交直径AB的延长于点D,若∠ABC=65°,则∠D的度数是( )
A.25°
B.30°
C.40°
D.50°
9.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD=6,则CB长( )
A.4
B.5
C.6
D.无法确定
10.如图,点I是△ABC的内心,∠BIC=130°,则∠BAC=( )
A.60°
B.65°
C.70°
D.80°
11.△ABC中,∠C=90°,内切圆与AB相切于点D,AD=2,BD=3,则△ABC的面积为( )
A.3
B.6
C.12
D.无法确定
二、填空题
12.如图,PA、PB切⊙O于A、B,点C在上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是
.
13.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为
.
三、解答题
14.如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.
15.已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,
(1)求证:DE是⊙O的切线.
(2)当BC=10,AD=4时,求⊙O的半径.
16.如图,已知△ABC内接于⊙O,过点B作直线EF∥AC,又知∠ACB=∠BDC=60°,AC=cm.
(1)请探究EF与⊙O的位置关系,并说明理由;
(2)求⊙O的周长.
17.如图,已知AB是⊙O的直径,∠DAC=∠B,判断AD与⊙O的位置关系,并说明理由.
18.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)如图1,证明:OD∥BC;
(2)如图2,若AD是⊙O的切线,连接BD交于⊙O于点F,连接EF,且OA=,求EF的长.
19.如图,⊙O的直径BE为4,∠BAE的平分线AD交⊙O于点D,交BE于点F,C是BE延长线上一点,且FC=AC.
(1)求BD的长;
(2)求证:AC是⊙O的切线.
20.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB
(1)求证:DC为⊙O的切线;
(2)若∠DAB=60°,⊙O的半径为3,求线段AC的长
21.如图,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC中点,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)设CD与OE的交点为F,若AB=10,BC=6,求OF的长.
参考答案
1.解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒)
∴⊙P与直线CD相切时,时间为4秒,
当点P在点O的右侧时,同法可得t=8秒
故选:D.
2.
解:连接BC,
∵DB、DE分别切⊙O于点B、C,
∴BD=DC,
∵∠ACE=25°,
∴∠ABC=25°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠DBC=∠DCB=90°﹣25°=65°,
∴∠D=50°.
故选:A.
3.解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,
∴AC=EC,DE=DB,PA=PB
∵△PCD的周长等于3,
∴PA+PB=3,
∴PA=.
故选:A.
4.解:过P点作大圆的直径CD,如图,设大圆半径为R,小圆半径为r,
∵PA?PB=PC?PD,
∴PA?PB=(OC﹣OP)?(OP+OD)
=(R﹣r)(R+r)
=R2﹣r2,
∵两同心圆间的圆环(即图中阴影部分)的面积为16π,
∴πR2﹣πr2=16π,
∴R2﹣r2=16,
∴PA?PB=16.
故选:A.
5.解:如图,⊙I与AB、AC、DE的切点为M、N、G,设DG=DM=x,EG=EN=y.
∵AM=AN==,
∴AD=﹣x,AE=﹣y,
∵DE∥BC,
∴x=,y=,
∴DE=x+y=+=.故选:B.
6.解:设这个三角形的内切圆半径是r,
∵三角形周长为12,面积为6,
∴×12r=6,
解得r=1.
故选:D.
7.解:连接AQ,AP.
根据切线的性质定理,得AQ⊥PQ;
要使PQ最小,只需AP最小,
根据垂线段最短,可知当AP⊥x轴时,AP最短,
∴P点的坐标是(﹣3,0).
故选:D.
8.解:连接OC,如图,
∵CD为切线,
∴OC⊥CD,
∴∠OCD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=90°﹣∠ABC=90°﹣65°=25°,
∴∠BCD=∠A=25°,
∵∠OBC=∠BCD+∠D
∴∠D=65°﹣25°=40°.
故选:C.
9.解:方法1、
设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH.
设CD=y,CB=x.
设S梯形ABCD=S
则S=(CD+AB)R=(y+10)R
S=S△BOC+S△COD+S△DOA
=xR+yR+×6R
联立(1)(2)得x=4;
方法2、连接OD.OC
∵AD,CD是⊙O的切线,
∴∠ADO=∠ODC,
∵CD∥AB,
∴∠ODC=∠AOD,
∴∠ADO=∠AOD
∴AD=OA
∵AD=6,
∴OA=6,
∵AB=10,
∴OB=4,
同理可得
OB=BC=4,
故选:A.
10.解:∵点I是△ABC的内心,
∴∠ABC=2∠IBC,∠ACB=2∠ICB,
∵∠BIC=130°,
∴∠IBC+∠ICB=180°﹣∠CIB=50°,
∴∠ABC+∠ACB=2×50°=100°,
∴∠BAC=180°﹣(∠ACB+∠ABC)=80°.
故选:D.
11.解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.
根据切线长定理,得AE=AD=2,BF=BD=3,CF=CE=x.
根据勾股定理,得(x+2)2+(x+3)2=(2+3)2.
整理,得x2+5x=6.
所以S△ABC=AC?BC
=(x+2)(x+3)
=(x2+5x+6)
=×(6+6)
=6.
故选:B.
12.解:连接OA、OB,如下图所示:
∵PA、PB为圆的两条切线,
∴由切线长定理可得:PA=PB,
同理可知:DA=DC,EC=EB;
∵OA⊥PA,OA=5,PO=13,
∴由勾股定理得:PA=12,
∴PA=PB=12;
∵△PDE的周长=PD+DC+CE+PE,DA=DC,EC=EB;
∴△PDE的周长=PD+DA+PE+EB=PA+PB=24,
故此题应该填24cm.
13.解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=25,
∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50,
故答案为:50.
14.解:△PDE是等腰三角形.
理由是:连接OD,
∵OC⊥AB,
∴∠CEO+∠OCE=90°,
∵OC=OD,
∴∠OCE=∠ODE,
∵PD切⊙O,
∴∠ODE+∠PDE=90°,
∵∠OEC=∠PED,
∴∠PDE=∠PED,
∴PD=PE,
∴△PDE是等腰三角形.
15.(1)证明:连接OE、OD,
在△AOD和△EOD中,
,
∴△AOD≌△EOD(SSS),
∴∠OED=∠BAC=90°,
∴DE是⊙O的切线;
(2)解:∵△AOD≌△EOD,
∴∠AOD=∠EOD,
∵OB=OE,
∴∠B=∠OEB,
∵∠AOE=∠B+∠OEB,
∴∠BEO=∠EOD,
∴OD∥BC,又AO=BO,
∴OD=BC=5,
由勾股定理得,AO==3,
则⊙O的半径为3.
16.解:(1)EF与⊙O相切.理由如下:
延长BO交AC于H,如图,
∵∠BAC=∠BDC=60°,
而∠ACB=60°,
∴△ABC为等边三角形,
∵点O为△ABC的外心,
∴BH⊥AC,
∵AC∥EF,
∴BH⊥EF,
∴EF为⊙O的切线;
(2)连接OA,如图,
∵△ABC为等边三角形,
∴OA平分∠ABC,
∴∠OAH=30°,
∵OH⊥AC,
∴AH=CH=AC=,
∴OA=1,
∴⊙O的周长=2π×1=2π(cm).
17.解:直线AD是⊙O的切线
∵AB是⊙O的直径
∴∠ACB=90°
∴∠B+∠BAC=90°
∵∠DAC=∠B,
∴∠DAC+∠BAC=90°
∴AB⊥AD,且AB是直径
∴AD是⊙O的切线
18.解:(1)连接OC,
在△OAD和△OCD中,
,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∴OD∥BC;
(2)连接AF,过F作FM⊥EF交OD于M,
∵AB=AD,AD是圆的切线,
∴△ABD为等腰直角三角形,
∵AB为直径,
∴∠AFB=90°,∠DAF=45°,
∵∠AED=∠AFD=90°,
∴∠DAF=∠ADF=45°,∠EAF=∠FDM,
∴AF=DF,
∵∠EFM=∠AFD=90°,
∴∠AFE=∠DFM,
∴△AEF≌△DMF(ASA),
∴AE=DM,
∵,OA=,
∴OD==5,
∴AE=DM==2,DE=4,
∴EM=4﹣2=2,
∴EF=.
19.(1)解:如图1,连接OD.
∵BE为⊙O的直径,
∴∠BAE=90°.
∵AD平分∠BAE,∠BAD=∠EAD=45°.
∴∠BOD=2∠BAD=90°.
∴Rt△BOD中,.
(2)证明:如图,连接OA.
∵AC=FC,
∴∠FAC=∠CFA.
∵∠DFO=∠CFA,
∴∠DFO=∠FAC.
∵OA=OD,
∴∠OAF=∠ODF.
由(1)知∠BOD=90°,
∴∠DFO+∠ODF=∠CAF+∠OAF=90°.
∴OA⊥AC于A,
∴AC是⊙O的切线.
20.(1)证明:连接CO,
∵AO=CO,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠OAC=∠DAC,
∴∠DAC=∠OCA,
∴CO∥AD,AD⊥CD,
∴CO⊥CD,
∴DC为⊙O的切线;
(2)连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠DAB=60°,AC平分∠DAB,
∴∠BAC=∠DAB=30°,
∵⊙O的半径为3,
∴AB=6,
∴AC=AB=3.
21.解:(1)DE与⊙O相切.
理由如下:连接CD、OD,如图,
∵BC为直径,
∴∠BDC=90°,
∵E为Rt△ADC的斜边AC的中点,
∴EA=ED,
∴∠1=∠A,
∵OB=OD,
∴∠B=∠2,
而∠B+∠A=90°
∴∠1+∠2=90°,
∴∠EDO=90°,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)∵∠DBC=∠CBA,∠BDC=∠BCA,
∴BD=,
∵OB=OC,EC=EA,
∴OE为△CAB的中位线,
∴OF∥BD,
∴OF:BD=OC:CB,
∴OF=BD=.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
