第6单元一次函数—一次函数解答题专题复习练习(拓展) 2021-2022学年苏科版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 第6单元一次函数—一次函数解答题专题复习练习(拓展) 2021-2022学年苏科版数学八年级上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 408.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 21:21:50 | ||
图片预览



文档简介
一次函数解答题专题复习练习(拓展)
一次函数的解析式与图象性质
1.已知直线l:y=kx+b与直线y=2x平行,且直线l过点(2,8).
(1)求直线l的解析式;
(2)求直线l与x轴的交点坐标.
2.在平面直角坐标系中,直线l1:y=kx+b(k、b为常数,且k≠0)经过A、B两点,点A在y轴上.
(1)若B点坐标为(﹣1,2).
①b=
(用含有字母k的代数式表示)
②当△OAB的面积为2时,求直线l1的表达式;
(2)若B点坐标为(k﹣2b,b﹣b2),点C(﹣1,s)也在直线l1上,
①求s的值;
②如果直线l1:y=kx+b(k≠0)与直线l2:y=x交于点(x1,y1),且0<x1<2,求k的取值范围.
一次函数与三角形
3.已知,正比例函数y=kx(k≠0)的经过点A(5,9)和点B(m,﹣3),点C(10,0)在x轴上,求这条直线的解析式和△ABC的面积.
4.已知:如图,在△AOB中,点E在线段AB上,A(3,2),B(5,0),E(4,m),求:
(1)直线AB的解析式;
(2)△AOE的面积.
5.已知正比例函数y=﹣x和一次函数y=kx+b的图象交于点A(a,2),一次函数的图象与y轴交于点B(0,4),与x轴交于点C.
(1)求a的值和一次函数表达式;
(2)求△AOC的面积.
6.已知一次函数的图象经过点(2,1)和点(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数与x轴、y轴的交点坐标,以及该函数图象与两坐标轴所围成的三角形的面积;
(3)若一条直线与此一次函数图象相交于(﹣1,a)点,且与y轴交点的纵坐标是5,求这条直线的解析式;
(4)求这两条直线与x轴所围成的三角形面积.
7.一次函数y=kx+b的图象经过点(3,﹣2)和点(﹣1,6).
(1)求出该一次函数的解析式;
(2)求该图象与x轴的交点A的坐标,与y轴的交点B的坐标,并画出函数的图象;
(3)该一次函数与正比例函数y=﹣x的图象交于点C,求△OAC的面积.
8.已知一次函数y=kx+b的图象经过点A(﹣4,0),B(2,6)两点.
(1)求一次函数y=kx+b的表达式.
(2)在直角坐标系中,画出这个函数的图象.
(3)求这个一次函数与坐标轴围成的三角形面积.
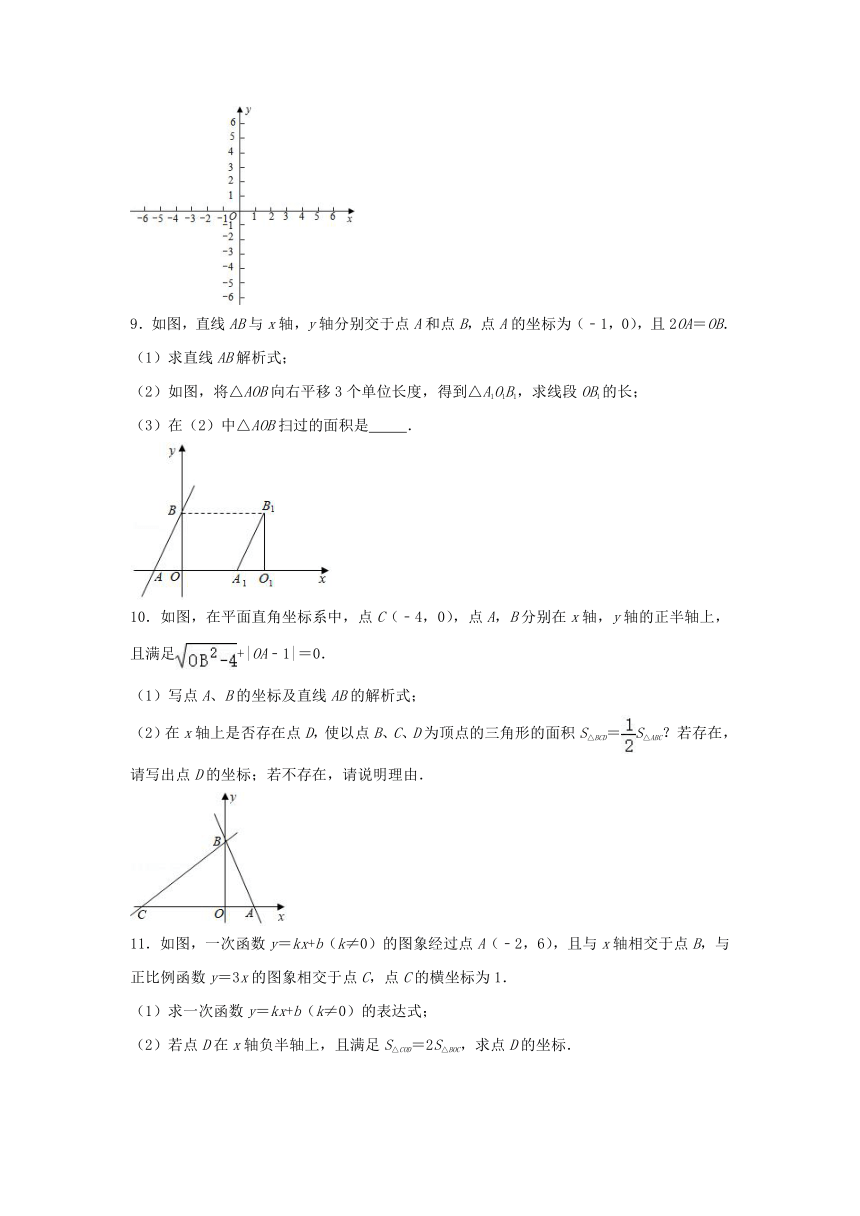
9.如图,直线AB与x轴,y轴分别交于点A和点B,点A的坐标为(﹣1,0),且2OA=OB.
(1)求直线AB解析式;
(2)如图,将△AOB向右平移3个单位长度,得到△A1O1B1,求线段OB1的长;
(3)在(2)中△AOB扫过的面积是
.
10.如图,在平面直角坐标系中,点C(﹣4,0),点A,B分别在x轴,y轴的正半轴上,且满足+|OA﹣1|=0.
(1)写点A、B的坐标及直线AB的解析式;
(2)在x轴上是否存在点D,使以点B、C、D为顶点的三角形的面积S△BCD=S△ABC?若存在,请写出点D的坐标;若不存在,请说明理由.
11.如图,一次函数y=kx+b(k≠0)的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求一次函数y=kx+b(k≠0)的表达式;
(2)若点D在x轴负半轴上,且满足S△COD=2S△BOC,求点D的坐标.
一次函数与三角形的存在性问题
12.如图,一次函数y=﹣x+4的图象与x轴和y轴分别交于点A和点B,以线段AB为边在第一象限内作等腰直角△ABC,使∠BAC=90°
(1)直接写出点A和点B的坐标:A(
,
);B(
,
);
(2)求O点到直线AB的距离;
(3)求出点C的坐标.
13.在平面直角坐标系xOy中,一次函数的解析式为y=mx﹣m+4(m为常数,且m≠0).
(1)若一次函数y=mx﹣m+4(m为常数,且m≠0)的图象经过点A(3,0),求一次函数的解析式;
(2)无论m取何值,一次函数y=mx﹣m+4(m为常数,且m≠0)的图象必经过一个固定的点B.
①求点B的坐标;
②在x轴上是否存在一点P,使得△PAB是等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
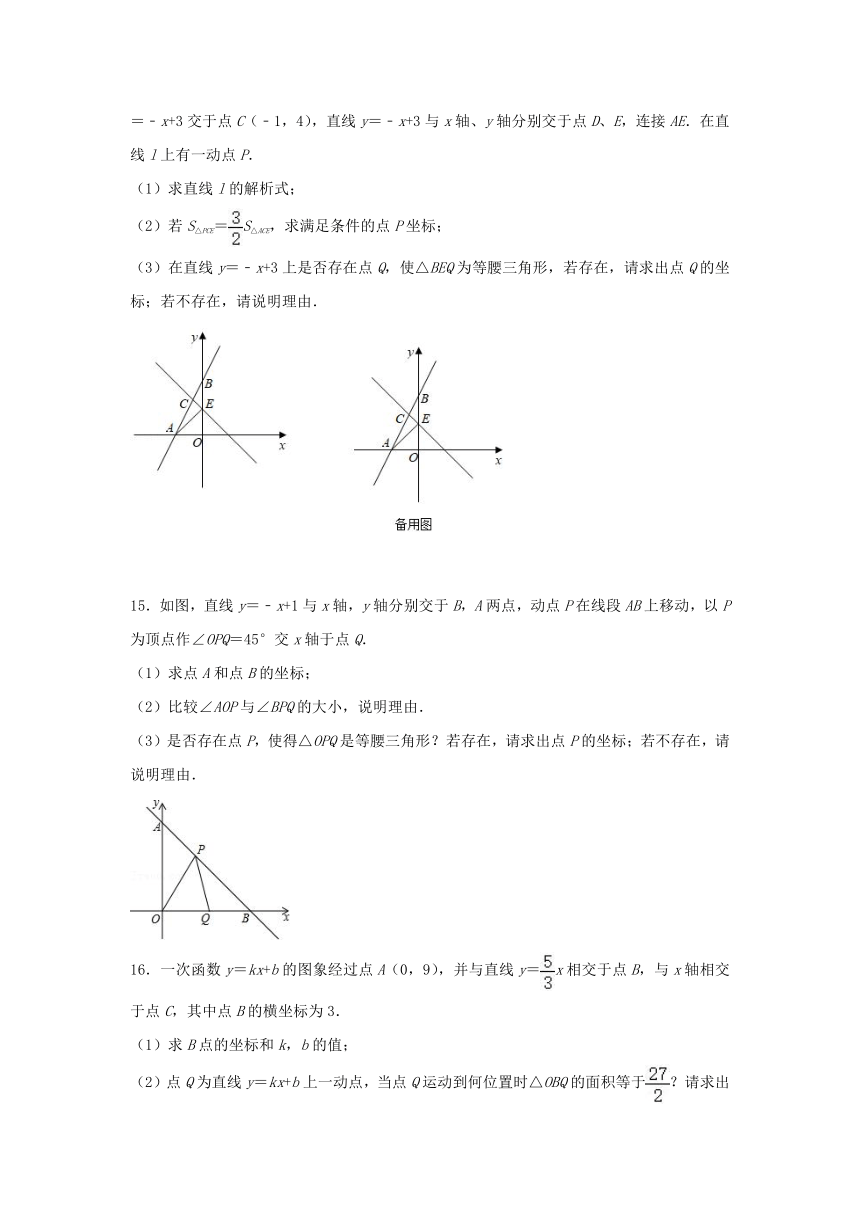
14.如图,在平面直角坐标系中,直线l与x轴、y轴分别交于点A,B(0,6),与直线y=﹣x+3交于点C(﹣1,4),直线y=﹣x+3与x轴、y轴分别交于点D、E,连接AE.在直线l上有一动点P.
(1)求直线l的解析式;
(2)若S△PCE=S△ACE,求满足条件的点P坐标;
(3)在直线y=﹣x+3上是否存在点Q,使△BEQ为等腰三角形,若存在,请求出点Q的坐标;若不存在,请说明理由.
15.如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.
(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
16.一次函数y=kx+b的图象经过点A(0,9),并与直线y=x相交于点B,与x轴相交于点C,其中点B的横坐标为3.
(1)求B点的坐标和k,b的值;
(2)点Q为直线y=kx+b上一动点,当点Q运动到何位置时△OBQ的面积等于?请求出点Q的坐标;
(3)在y轴上是否存在点P使△PAB是等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由.
一次函数与四边形
17.如图:直线y=﹣x+5分别与x轴,y轴交于A、B两点,
(1)求出A、B两点的坐标,计算AB的长度;
(2)若点C在x轴上,当△ABC为等腰三角形时,直接写出点C的坐标;(不写解答过程)
(3)已知两点E(1,0),F(3,0),若点G在边AB上,点H在边OB上,画图并求出四边形EFGH周长的最小值.
18.如图,直线l1:y=kx+b分别交x轴、y轴于点B(4,0)、N,直线l2:y=2x﹣1分别交x轴、y轴于点M、A,l1,l2交点P的坐标(m,2),请根据图象所提供的信息解答下列问题:
(1)当x=
时,kx+b≥2x﹣1;
(2)不等式kx+b<0的解集是
;
(3)在平面内是否存在一点H,使得以A,B,P,H四点组成的四边形是平行四边形.若存在,直接写出点H的坐标,若不存在,说明理由.
参考答案
1.解:(1)∵直线y=kx+b和直线y=2x平行,∴k=2,
把(2,8)代入y=2x+b得8=4+b,解得b=4,
∴直线解析式为y=2x+4,
(2)当y=0时,2x+4=0,解得x=﹣2,
∴直线l与x轴的交点坐标为(﹣2,0).
2.解:(1)①把B(﹣1,2)代入y=kx+b,
得b=2+k.故答案为2+k;
②∵点A在y轴上,∴A(0,b),
当b>0时,S△OAB=×b×1=2解得b=4,
∵b=2+k,∴k=2∴直线l1的表达式为:y=2x+4,
当b<0时,S△OAB=×(﹣b)×1=2解得b=﹣4,
∵b=2+k,∴k=﹣6∴直线l1的表达式为:y=﹣6x﹣4,
综上,直线l1的表达式为:y=2x+4或y=﹣6x﹣4;
(2)①∵直线l1:y=kx+b经过点B(k﹣2b,b﹣b2)和点C(﹣1,s).
∴k(k﹣2b)+b=b﹣b2,﹣k+b=s
整理得,(b﹣k)2=0,所以s=b﹣k=0.
②∵直线l1:y=kx+b(k≠0)与直线l2:y=x交于点(x1,y1),
∴kx1+b=x1
(1﹣k)x1=b,
∵b﹣k=0
∴b=k
∴x1=
∵0<x1<2,
∴>0或<2
解得0<k<.
答:k的取值范围是0<k<.
3.解:∵正比例函数y=kx(k≠0)的经过点A(5,9)和点B(m,﹣3),
∴9=5k,得k=1.8,
∴y=1.8x,
当y=﹣3时,﹣3=1.8x,得x=,
当y=0时,x=0,
∴点B(﹣,﹣3),函数y=1.8x与x轴的交点为(0,0),
∵点A(5,9),点B(﹣,﹣3),点C(10,0),
∴△ABC的面积是:=60,
即这条直线的解析式是y=1.8x,△ABC的面积是60.
4.解:(1)设直线AB的解析式为y=kx+b,
把A(3,2),B(5,0)代入得,
解得,,
∴直线AB的解析式为y=﹣x+5;
(2)把E(4,m)代入y=﹣x+5得,m=﹣4+5=1,
∴E(4,1),
∴,,
∴.
5.解:(1)将A(a,2)代入y=﹣x,
得:2=﹣a,
则a=﹣2,
∴A(﹣2,2),
将A(﹣2,2)和B(0,4)代入
y=kx+b中,
得:,
解得:,
则一次函数表达式为y=x+4;
(2)把y=0代入y=x+4,得x=﹣4,
∴C(﹣4,0),
∴S△AOC==4.
6.解:(1)设一次函数解析式为y=kx+b,
把(2,1),(﹣1,﹣3)代入得得,
所以一次函数解析式为y=x﹣;
(2)当x=0时,y=x﹣=﹣;则一次函数与y轴的交点坐标为(0,﹣);
当y=0时,x﹣=0,解得x=,则一次函数与x轴的交点坐标为(,0);
所以该函数图象与两坐标轴所围成的三角形的面积=××=;
(3)把(﹣1,a)代入y=x﹣得a=?(﹣1)﹣=﹣3,则直线与此一次函数的图象交点坐标为(﹣1,﹣3),
设这条直线的解析式为y=mx+n,
把(﹣1,﹣3)、(0,5)代入得,解得,
所以这条直线的表达式为y=8x+5;
(4)当x=0时,y=8x+5=5;当y=0时,8x+5=0,解得x=﹣,
所以直线y=3x+5与坐标轴的交点坐标为(0,5)、(﹣,0),
所以这两条直线与x轴所围成的三角形的面积=×3×(+)=.
7.解:(1)设一次函数的解析式为y=kx+b,则有,解得,
∴一次函数的解析式为y=﹣2x+4.
(2)对于直线y=﹣2x+4,令x=0,得到y=4,令y=0得到x=2,
∴A(2,0),B(0,4),
画出函数的图象如图所示;
(3)由,解得,
∴C(4,﹣4),
∴S△AOC=×2×4=4.
8.解:(1)∵一次函数y=kx+b的图象经过两点A(﹣4,0)、B(2,6),
∴,∴函数解析式为:y=x+4;
(2)函数图象如图
;
(3)一次函数y=x+4与y轴的交点为C(0,4),
∴△AOC的面积=4×4÷2=8.
9.解:(1)∵点A的坐标为(﹣1,0),
∴OA=1,
∵OB=2OA=2,
∴B(0,2),
把A(﹣1,0)和B(0,2)代入y=kx+b中得:,解得,
∴直线AB解析式为:y=2x+2;
(2)∵∠AOB=90°,
∴∠AO1B1=90°,
由平移得:OO1=3,O1B1=OB=2,
由勾股定理得:OB1==,
即线段OB1的长是;
(3)△ABC扫过的面积等于长方形OBB1O1与△AOB的面积的和,
即△AOB扫过的面积=3×2+×1×2=7,
故答案为7.
10.(1)依题意得OB2﹣4=0,OA﹣1=0,
∴OB=2,OA=1,
∴A的坐标为(1,0),B的坐标为(0,2),
设AB的解析式为y=kx+2
将A坐标代入得0=k+2,
∴k=﹣2
∴y=﹣2x+2;
(2)存在,
设D的坐标为(x,0),
∵A的坐标为(1,0),B的坐标为(0,2),点C(﹣4,0),
∴AC=5,
∴S△ABC==5,
∵S△BCD=S△ABC,
∴S△BCD==,即|x﹣(﹣4)|×2=,
∴|x+4|=,
∴x=﹣或x=﹣,
∴D的坐标为(﹣,0)或(﹣,0).
11.解:(1)∵点C是y=3x的一个点,且横坐标为1,
∴C(1,3),
把点A(﹣2,6)、C(1,3)代入y=kx+b得,解得,
∴一次函数的表达式为y=﹣x+4;
(2)由y=﹣x+4得B(4,0),
∵△COD和△BOC同高,且S△COD=2S△BOC,
∴OD=2OB,
∴D(﹣8,0)
12.解:(1)对于一次函数y=﹣x+4,
令x=0,得到y=4,即B(0,4);令y=0,得到y=3,即A(3,0);
故答案为:3,0;0,4;
(2)由(1)得到OA=3,OB=4,
在Rt△AOB中,根据勾股定理得:AB=5,
过O作OE⊥AB,
∴OA?OB=AB?OE,即OE==,
则点O到直线AB的距离为;
(3)过C作CD⊥x轴,可得∠BOA=∠ADC=90°,
∴∠ABO+∠BAO=90°,
∵△BAC为等腰直角三角形,
∴AB=AC,且∠BAC=90°,
∴∠BAO+∠CAD=90°,
∴∠ABO=∠CAD,
在△ABO和△CAD中,
,
∴△ABO≌△CAD(AAS),
∴AO=CD=3,BO=AD=4,
∴OD=OA+AD=3+4=7,
则C(7,3).
13.解:(1)将A(3,0)代入y=mx﹣m+4,
∴3m﹣m+4=0,
∴m=﹣2,
∴一次函数的解析式为y=﹣2x+6;
(2)①∵y=mx﹣m+4,
∴y=(x﹣1)m+4,
根据题意得x﹣1=0,
∴x=1,
则当x=1时,y=4,
所以B(1,4);
②设点P(x,0),
∵点A(3,0),点B(1,4),点P(x,0),
∴AB==2,AP=|3﹣x|,BP=,
当AB=AP时,
∴|3﹣x|=2,
∴x1=3+2,x2=3﹣2,
∴点P坐标为(3+2,0)或(3﹣2,0);
若AB=BP时,
∴=2,
∴x3=﹣1,x4=3(不合题意舍去),
∴点P坐标为(﹣1,0);
若AP=BP时,
∴=|3﹣x|,
∴x=﹣2,
∴点P坐标为(﹣2,0);
综上所述:点P的坐标为(3+2,0)或(3﹣2,0)或(﹣1,0)或(﹣2,0).
14.解:(1)直线l过点B,则设直线l的表达式为y=kx+6,
将点C的坐标代入上式得:4=﹣k+6,解得k=2,
故直线l的表达式为y=2x+6①;
(2)对于y=2x+6,令y=2x+6=0,解得x=﹣3,故点A(﹣3,0),
对于y=﹣x+3,令x=0,则y=3,故点E(0,3),
①当点P在直线CD的上方时,
过点A作直线k∥CD交y轴于点H,作直线m∥CD交y轴于点M,
∵S△PCE=S△ACE,则直线m与直线CD之间的距离和直线k与直线CD之间的距离为3:2,
则ME=EH,
∵直线k∥CD,设直线k的表达式为y=﹣x+b,将点A的坐标代入上式得:0=3+b,解得b=﹣3,
故点H(0,﹣3),
∵ME=EH=×(3+3)=9,
故点M的坐标为(0,12),
同理可得,直线m的表达式为y=﹣x+12②,
联立①②并解得,
故点P(2,10);
②当点P在直线CD的下方时,
同理可得,点P(﹣4,﹣2);
综上,点P的坐标为(2,10)或(﹣4,﹣2);
(3)存在,理由:
设点Q(m,3﹣m),
由点B、E、Q的坐标得:BQ2=m2+(3﹣m﹣6)2,BE2=9,QE2=2m2,
当BQ=BE时,即m2+(3﹣m﹣6)2=9,解得m=0(舍去)﹣3;
当BQ=EQ时,同理可得:m=﹣;
当BE=QE时,同理可得:m=±;
综上,点Q的坐标为(,3﹣)或(﹣,3+)或(﹣,)或(﹣3,6).
15.解:(1)∵直线y=﹣x+1与x轴,y轴分别交于B,A两点,
令x=0,则y=0+1=1,∴A(0,1),
令y=0,则0=﹣x+1,解得:x=1.∴B(1,0).
(2)∠AOP=∠BPQ.
理由如下:
过P点作PE⊥OA交OA于点E,
∵A(0,1),B(1,0).
∴OA=OB=1,
∴∠OAB=∠OBA=45°,
∵PE⊥OA,
∴∠APE=45°,
∵∠OPQ=45°,
∴∠OPE+∠BPQ=90°,
∵∠AOP+∠OPE=90°,
∴∠AOP=∠BPQ.
(3)△OPQ可以是等腰三角形.
理由如下:
如图,过P点PE⊥OA交OA于点E,
(ⅰ)若OP=OQ,
则∠OPQ=∠OQP,
∴∠POQ=90°,
∴点P与点A重合,
∴点P坐标为(0,1),
(ⅱ)若QP=QO,
则∠OPQ=∠QOP=45°,
所以PQ⊥QO,
可设P(x,x)代入y=﹣x+1得x=,
∴点P坐标为(,),
(ⅲ)
若PO=PQ
∵∠OPQ+∠1=∠2+∠3,
而∠OPQ=∠3=45°,
∴∠1=∠2,
又∵∠3=∠4=45°,
∴△AOP≌△BPQ(AAS),
PB=OA=1,
∴AP=﹣1
由勾股定理求得PE=AE=1﹣,
∴EO=,
∴点P坐标为(1﹣,),
∴点P坐标为(0,1),(,)或(1﹣,)时,△OPQ是等腰三角形.
16.解:(1)y=x相交于点B,则点B(3,5),
将点A、B的坐标代入一次函数表达式并解得:k=﹣,b=9;
(2)设点Q(m,﹣m+9),
则△OBQ的面积=×OA×|xQ﹣xB|=9×|m﹣3|=,
解得:m=0或6,
故点Q(0,9)或(6,1);
(3)设点P(0,m),而点A、B的坐标分别为:(0,9)、(3,5),
则AB2=25,AP2=(m﹣9)2,BP2=9+(m﹣5)2,
当AB=AP时,25=(m﹣9)2,解得:m=14或4;
当AB=BP时,同理可得:m=9(舍去)或1;
当AP=BP时,同理可得:m=;
综上点P的坐标为:(0,4)或(0,14)或(0,1)或(0,)
17.解:(1)对于y=﹣x+5,令x=0,则y=5,令y=﹣x+5=0,解得x=5,
故点A、B的坐标分别为(5,0)、(0,5),则AB==5;
(2)设点C(x,0),
则AB2=50,AC2=(x﹣5)2,BC2=x2+25,
当AB=AC时,50=(x﹣5)2,解得x=5±5;
当AB=BC时,同理可得x=5(舍去)或﹣5;
当AC=BC时,同理可得x=0;
故点C的坐标为(0,0)或(﹣5,0)或(5+5,0)或(5﹣5,0);
(3)作点F关于直线AB的对称点M,作点E关于y轴的对称点N(﹣1,0),
连接MN交y轴于点H,交AB于点G,则点H、G为所求点,
∴GF=GM,HN=HE,
则四边形EFGH周长=EF+GF+HG+EH=EF+GM+HN+GH=EF+MN为最小,
从作图看,点M(5,2),
则MN==2,
故四边形EFGH周长最小值=EF+MN=2+2.
18.解:(1)将点P的坐标代入y=2x﹣1得,2=2m﹣1,解得m=1.5,故点P(1.5,2),
从图象看,当x≤1.5时,kx+b≥2x﹣1,故答案为:≤1.5;
(2)从图象看,不等式kx+b<0的解集是x>4,故答案为x>
(3)∵直线l2:y=2x﹣1交y轴于点A,故点A(0,﹣1),
设点H(s,t),
①当AB是边时,
点A向右平移4个单位向上平移1个单位得到点B,同样点P(H)向右平移4个单位向上平移1个单位得到H(P),
则1.5±4=s且2±1=t,解得,
故点H的坐标为(5.5,3)或(﹣2.5,1);
②当AB是对角线时,
由中点公式得:(0+4)=(s+1.5)且(﹣1+0)=(t+2),解得,
故点H的坐标为(2.5,﹣3).
综上,点H的坐标为(5.5,3)或(﹣2.5,1)或(2.5,﹣3).
一次函数的解析式与图象性质
1.已知直线l:y=kx+b与直线y=2x平行,且直线l过点(2,8).
(1)求直线l的解析式;
(2)求直线l与x轴的交点坐标.
2.在平面直角坐标系中,直线l1:y=kx+b(k、b为常数,且k≠0)经过A、B两点,点A在y轴上.
(1)若B点坐标为(﹣1,2).
①b=
(用含有字母k的代数式表示)
②当△OAB的面积为2时,求直线l1的表达式;
(2)若B点坐标为(k﹣2b,b﹣b2),点C(﹣1,s)也在直线l1上,
①求s的值;
②如果直线l1:y=kx+b(k≠0)与直线l2:y=x交于点(x1,y1),且0<x1<2,求k的取值范围.
一次函数与三角形
3.已知,正比例函数y=kx(k≠0)的经过点A(5,9)和点B(m,﹣3),点C(10,0)在x轴上,求这条直线的解析式和△ABC的面积.
4.已知:如图,在△AOB中,点E在线段AB上,A(3,2),B(5,0),E(4,m),求:
(1)直线AB的解析式;
(2)△AOE的面积.
5.已知正比例函数y=﹣x和一次函数y=kx+b的图象交于点A(a,2),一次函数的图象与y轴交于点B(0,4),与x轴交于点C.
(1)求a的值和一次函数表达式;
(2)求△AOC的面积.
6.已知一次函数的图象经过点(2,1)和点(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数与x轴、y轴的交点坐标,以及该函数图象与两坐标轴所围成的三角形的面积;
(3)若一条直线与此一次函数图象相交于(﹣1,a)点,且与y轴交点的纵坐标是5,求这条直线的解析式;
(4)求这两条直线与x轴所围成的三角形面积.
7.一次函数y=kx+b的图象经过点(3,﹣2)和点(﹣1,6).
(1)求出该一次函数的解析式;
(2)求该图象与x轴的交点A的坐标,与y轴的交点B的坐标,并画出函数的图象;
(3)该一次函数与正比例函数y=﹣x的图象交于点C,求△OAC的面积.
8.已知一次函数y=kx+b的图象经过点A(﹣4,0),B(2,6)两点.
(1)求一次函数y=kx+b的表达式.
(2)在直角坐标系中,画出这个函数的图象.
(3)求这个一次函数与坐标轴围成的三角形面积.
9.如图,直线AB与x轴,y轴分别交于点A和点B,点A的坐标为(﹣1,0),且2OA=OB.
(1)求直线AB解析式;
(2)如图,将△AOB向右平移3个单位长度,得到△A1O1B1,求线段OB1的长;
(3)在(2)中△AOB扫过的面积是
.
10.如图,在平面直角坐标系中,点C(﹣4,0),点A,B分别在x轴,y轴的正半轴上,且满足+|OA﹣1|=0.
(1)写点A、B的坐标及直线AB的解析式;
(2)在x轴上是否存在点D,使以点B、C、D为顶点的三角形的面积S△BCD=S△ABC?若存在,请写出点D的坐标;若不存在,请说明理由.
11.如图,一次函数y=kx+b(k≠0)的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求一次函数y=kx+b(k≠0)的表达式;
(2)若点D在x轴负半轴上,且满足S△COD=2S△BOC,求点D的坐标.
一次函数与三角形的存在性问题
12.如图,一次函数y=﹣x+4的图象与x轴和y轴分别交于点A和点B,以线段AB为边在第一象限内作等腰直角△ABC,使∠BAC=90°
(1)直接写出点A和点B的坐标:A(
,
);B(
,
);
(2)求O点到直线AB的距离;
(3)求出点C的坐标.
13.在平面直角坐标系xOy中,一次函数的解析式为y=mx﹣m+4(m为常数,且m≠0).
(1)若一次函数y=mx﹣m+4(m为常数,且m≠0)的图象经过点A(3,0),求一次函数的解析式;
(2)无论m取何值,一次函数y=mx﹣m+4(m为常数,且m≠0)的图象必经过一个固定的点B.
①求点B的坐标;
②在x轴上是否存在一点P,使得△PAB是等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
14.如图,在平面直角坐标系中,直线l与x轴、y轴分别交于点A,B(0,6),与直线y=﹣x+3交于点C(﹣1,4),直线y=﹣x+3与x轴、y轴分别交于点D、E,连接AE.在直线l上有一动点P.
(1)求直线l的解析式;
(2)若S△PCE=S△ACE,求满足条件的点P坐标;
(3)在直线y=﹣x+3上是否存在点Q,使△BEQ为等腰三角形,若存在,请求出点Q的坐标;若不存在,请说明理由.
15.如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.
(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
16.一次函数y=kx+b的图象经过点A(0,9),并与直线y=x相交于点B,与x轴相交于点C,其中点B的横坐标为3.
(1)求B点的坐标和k,b的值;
(2)点Q为直线y=kx+b上一动点,当点Q运动到何位置时△OBQ的面积等于?请求出点Q的坐标;
(3)在y轴上是否存在点P使△PAB是等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由.
一次函数与四边形
17.如图:直线y=﹣x+5分别与x轴,y轴交于A、B两点,
(1)求出A、B两点的坐标,计算AB的长度;
(2)若点C在x轴上,当△ABC为等腰三角形时,直接写出点C的坐标;(不写解答过程)
(3)已知两点E(1,0),F(3,0),若点G在边AB上,点H在边OB上,画图并求出四边形EFGH周长的最小值.
18.如图,直线l1:y=kx+b分别交x轴、y轴于点B(4,0)、N,直线l2:y=2x﹣1分别交x轴、y轴于点M、A,l1,l2交点P的坐标(m,2),请根据图象所提供的信息解答下列问题:
(1)当x=
时,kx+b≥2x﹣1;
(2)不等式kx+b<0的解集是
;
(3)在平面内是否存在一点H,使得以A,B,P,H四点组成的四边形是平行四边形.若存在,直接写出点H的坐标,若不存在,说明理由.
参考答案
1.解:(1)∵直线y=kx+b和直线y=2x平行,∴k=2,
把(2,8)代入y=2x+b得8=4+b,解得b=4,
∴直线解析式为y=2x+4,
(2)当y=0时,2x+4=0,解得x=﹣2,
∴直线l与x轴的交点坐标为(﹣2,0).
2.解:(1)①把B(﹣1,2)代入y=kx+b,
得b=2+k.故答案为2+k;
②∵点A在y轴上,∴A(0,b),
当b>0时,S△OAB=×b×1=2解得b=4,
∵b=2+k,∴k=2∴直线l1的表达式为:y=2x+4,
当b<0时,S△OAB=×(﹣b)×1=2解得b=﹣4,
∵b=2+k,∴k=﹣6∴直线l1的表达式为:y=﹣6x﹣4,
综上,直线l1的表达式为:y=2x+4或y=﹣6x﹣4;
(2)①∵直线l1:y=kx+b经过点B(k﹣2b,b﹣b2)和点C(﹣1,s).
∴k(k﹣2b)+b=b﹣b2,﹣k+b=s
整理得,(b﹣k)2=0,所以s=b﹣k=0.
②∵直线l1:y=kx+b(k≠0)与直线l2:y=x交于点(x1,y1),
∴kx1+b=x1
(1﹣k)x1=b,
∵b﹣k=0
∴b=k
∴x1=
∵0<x1<2,
∴>0或<2
解得0<k<.
答:k的取值范围是0<k<.
3.解:∵正比例函数y=kx(k≠0)的经过点A(5,9)和点B(m,﹣3),
∴9=5k,得k=1.8,
∴y=1.8x,
当y=﹣3时,﹣3=1.8x,得x=,
当y=0时,x=0,
∴点B(﹣,﹣3),函数y=1.8x与x轴的交点为(0,0),
∵点A(5,9),点B(﹣,﹣3),点C(10,0),
∴△ABC的面积是:=60,
即这条直线的解析式是y=1.8x,△ABC的面积是60.
4.解:(1)设直线AB的解析式为y=kx+b,
把A(3,2),B(5,0)代入得,
解得,,
∴直线AB的解析式为y=﹣x+5;
(2)把E(4,m)代入y=﹣x+5得,m=﹣4+5=1,
∴E(4,1),
∴,,
∴.
5.解:(1)将A(a,2)代入y=﹣x,
得:2=﹣a,
则a=﹣2,
∴A(﹣2,2),
将A(﹣2,2)和B(0,4)代入
y=kx+b中,
得:,
解得:,
则一次函数表达式为y=x+4;
(2)把y=0代入y=x+4,得x=﹣4,
∴C(﹣4,0),
∴S△AOC==4.
6.解:(1)设一次函数解析式为y=kx+b,
把(2,1),(﹣1,﹣3)代入得得,
所以一次函数解析式为y=x﹣;
(2)当x=0时,y=x﹣=﹣;则一次函数与y轴的交点坐标为(0,﹣);
当y=0时,x﹣=0,解得x=,则一次函数与x轴的交点坐标为(,0);
所以该函数图象与两坐标轴所围成的三角形的面积=××=;
(3)把(﹣1,a)代入y=x﹣得a=?(﹣1)﹣=﹣3,则直线与此一次函数的图象交点坐标为(﹣1,﹣3),
设这条直线的解析式为y=mx+n,
把(﹣1,﹣3)、(0,5)代入得,解得,
所以这条直线的表达式为y=8x+5;
(4)当x=0时,y=8x+5=5;当y=0时,8x+5=0,解得x=﹣,
所以直线y=3x+5与坐标轴的交点坐标为(0,5)、(﹣,0),
所以这两条直线与x轴所围成的三角形的面积=×3×(+)=.
7.解:(1)设一次函数的解析式为y=kx+b,则有,解得,
∴一次函数的解析式为y=﹣2x+4.
(2)对于直线y=﹣2x+4,令x=0,得到y=4,令y=0得到x=2,
∴A(2,0),B(0,4),
画出函数的图象如图所示;
(3)由,解得,
∴C(4,﹣4),
∴S△AOC=×2×4=4.
8.解:(1)∵一次函数y=kx+b的图象经过两点A(﹣4,0)、B(2,6),
∴,∴函数解析式为:y=x+4;
(2)函数图象如图
;
(3)一次函数y=x+4与y轴的交点为C(0,4),
∴△AOC的面积=4×4÷2=8.
9.解:(1)∵点A的坐标为(﹣1,0),
∴OA=1,
∵OB=2OA=2,
∴B(0,2),
把A(﹣1,0)和B(0,2)代入y=kx+b中得:,解得,
∴直线AB解析式为:y=2x+2;
(2)∵∠AOB=90°,
∴∠AO1B1=90°,
由平移得:OO1=3,O1B1=OB=2,
由勾股定理得:OB1==,
即线段OB1的长是;
(3)△ABC扫过的面积等于长方形OBB1O1与△AOB的面积的和,
即△AOB扫过的面积=3×2+×1×2=7,
故答案为7.
10.(1)依题意得OB2﹣4=0,OA﹣1=0,
∴OB=2,OA=1,
∴A的坐标为(1,0),B的坐标为(0,2),
设AB的解析式为y=kx+2
将A坐标代入得0=k+2,
∴k=﹣2
∴y=﹣2x+2;
(2)存在,
设D的坐标为(x,0),
∵A的坐标为(1,0),B的坐标为(0,2),点C(﹣4,0),
∴AC=5,
∴S△ABC==5,
∵S△BCD=S△ABC,
∴S△BCD==,即|x﹣(﹣4)|×2=,
∴|x+4|=,
∴x=﹣或x=﹣,
∴D的坐标为(﹣,0)或(﹣,0).
11.解:(1)∵点C是y=3x的一个点,且横坐标为1,
∴C(1,3),
把点A(﹣2,6)、C(1,3)代入y=kx+b得,解得,
∴一次函数的表达式为y=﹣x+4;
(2)由y=﹣x+4得B(4,0),
∵△COD和△BOC同高,且S△COD=2S△BOC,
∴OD=2OB,
∴D(﹣8,0)
12.解:(1)对于一次函数y=﹣x+4,
令x=0,得到y=4,即B(0,4);令y=0,得到y=3,即A(3,0);
故答案为:3,0;0,4;
(2)由(1)得到OA=3,OB=4,
在Rt△AOB中,根据勾股定理得:AB=5,
过O作OE⊥AB,
∴OA?OB=AB?OE,即OE==,
则点O到直线AB的距离为;
(3)过C作CD⊥x轴,可得∠BOA=∠ADC=90°,
∴∠ABO+∠BAO=90°,
∵△BAC为等腰直角三角形,
∴AB=AC,且∠BAC=90°,
∴∠BAO+∠CAD=90°,
∴∠ABO=∠CAD,
在△ABO和△CAD中,
,
∴△ABO≌△CAD(AAS),
∴AO=CD=3,BO=AD=4,
∴OD=OA+AD=3+4=7,
则C(7,3).
13.解:(1)将A(3,0)代入y=mx﹣m+4,
∴3m﹣m+4=0,
∴m=﹣2,
∴一次函数的解析式为y=﹣2x+6;
(2)①∵y=mx﹣m+4,
∴y=(x﹣1)m+4,
根据题意得x﹣1=0,
∴x=1,
则当x=1时,y=4,
所以B(1,4);
②设点P(x,0),
∵点A(3,0),点B(1,4),点P(x,0),
∴AB==2,AP=|3﹣x|,BP=,
当AB=AP时,
∴|3﹣x|=2,
∴x1=3+2,x2=3﹣2,
∴点P坐标为(3+2,0)或(3﹣2,0);
若AB=BP时,
∴=2,
∴x3=﹣1,x4=3(不合题意舍去),
∴点P坐标为(﹣1,0);
若AP=BP时,
∴=|3﹣x|,
∴x=﹣2,
∴点P坐标为(﹣2,0);
综上所述:点P的坐标为(3+2,0)或(3﹣2,0)或(﹣1,0)或(﹣2,0).
14.解:(1)直线l过点B,则设直线l的表达式为y=kx+6,
将点C的坐标代入上式得:4=﹣k+6,解得k=2,
故直线l的表达式为y=2x+6①;
(2)对于y=2x+6,令y=2x+6=0,解得x=﹣3,故点A(﹣3,0),
对于y=﹣x+3,令x=0,则y=3,故点E(0,3),
①当点P在直线CD的上方时,
过点A作直线k∥CD交y轴于点H,作直线m∥CD交y轴于点M,
∵S△PCE=S△ACE,则直线m与直线CD之间的距离和直线k与直线CD之间的距离为3:2,
则ME=EH,
∵直线k∥CD,设直线k的表达式为y=﹣x+b,将点A的坐标代入上式得:0=3+b,解得b=﹣3,
故点H(0,﹣3),
∵ME=EH=×(3+3)=9,
故点M的坐标为(0,12),
同理可得,直线m的表达式为y=﹣x+12②,
联立①②并解得,
故点P(2,10);
②当点P在直线CD的下方时,
同理可得,点P(﹣4,﹣2);
综上,点P的坐标为(2,10)或(﹣4,﹣2);
(3)存在,理由:
设点Q(m,3﹣m),
由点B、E、Q的坐标得:BQ2=m2+(3﹣m﹣6)2,BE2=9,QE2=2m2,
当BQ=BE时,即m2+(3﹣m﹣6)2=9,解得m=0(舍去)﹣3;
当BQ=EQ时,同理可得:m=﹣;
当BE=QE时,同理可得:m=±;
综上,点Q的坐标为(,3﹣)或(﹣,3+)或(﹣,)或(﹣3,6).
15.解:(1)∵直线y=﹣x+1与x轴,y轴分别交于B,A两点,
令x=0,则y=0+1=1,∴A(0,1),
令y=0,则0=﹣x+1,解得:x=1.∴B(1,0).
(2)∠AOP=∠BPQ.
理由如下:
过P点作PE⊥OA交OA于点E,
∵A(0,1),B(1,0).
∴OA=OB=1,
∴∠OAB=∠OBA=45°,
∵PE⊥OA,
∴∠APE=45°,
∵∠OPQ=45°,
∴∠OPE+∠BPQ=90°,
∵∠AOP+∠OPE=90°,
∴∠AOP=∠BPQ.
(3)△OPQ可以是等腰三角形.
理由如下:
如图,过P点PE⊥OA交OA于点E,
(ⅰ)若OP=OQ,
则∠OPQ=∠OQP,
∴∠POQ=90°,
∴点P与点A重合,
∴点P坐标为(0,1),
(ⅱ)若QP=QO,
则∠OPQ=∠QOP=45°,
所以PQ⊥QO,
可设P(x,x)代入y=﹣x+1得x=,
∴点P坐标为(,),
(ⅲ)
若PO=PQ
∵∠OPQ+∠1=∠2+∠3,
而∠OPQ=∠3=45°,
∴∠1=∠2,
又∵∠3=∠4=45°,
∴△AOP≌△BPQ(AAS),
PB=OA=1,
∴AP=﹣1
由勾股定理求得PE=AE=1﹣,
∴EO=,
∴点P坐标为(1﹣,),
∴点P坐标为(0,1),(,)或(1﹣,)时,△OPQ是等腰三角形.
16.解:(1)y=x相交于点B,则点B(3,5),
将点A、B的坐标代入一次函数表达式并解得:k=﹣,b=9;
(2)设点Q(m,﹣m+9),
则△OBQ的面积=×OA×|xQ﹣xB|=9×|m﹣3|=,
解得:m=0或6,
故点Q(0,9)或(6,1);
(3)设点P(0,m),而点A、B的坐标分别为:(0,9)、(3,5),
则AB2=25,AP2=(m﹣9)2,BP2=9+(m﹣5)2,
当AB=AP时,25=(m﹣9)2,解得:m=14或4;
当AB=BP时,同理可得:m=9(舍去)或1;
当AP=BP时,同理可得:m=;
综上点P的坐标为:(0,4)或(0,14)或(0,1)或(0,)
17.解:(1)对于y=﹣x+5,令x=0,则y=5,令y=﹣x+5=0,解得x=5,
故点A、B的坐标分别为(5,0)、(0,5),则AB==5;
(2)设点C(x,0),
则AB2=50,AC2=(x﹣5)2,BC2=x2+25,
当AB=AC时,50=(x﹣5)2,解得x=5±5;
当AB=BC时,同理可得x=5(舍去)或﹣5;
当AC=BC时,同理可得x=0;
故点C的坐标为(0,0)或(﹣5,0)或(5+5,0)或(5﹣5,0);
(3)作点F关于直线AB的对称点M,作点E关于y轴的对称点N(﹣1,0),
连接MN交y轴于点H,交AB于点G,则点H、G为所求点,
∴GF=GM,HN=HE,
则四边形EFGH周长=EF+GF+HG+EH=EF+GM+HN+GH=EF+MN为最小,
从作图看,点M(5,2),
则MN==2,
故四边形EFGH周长最小值=EF+MN=2+2.
18.解:(1)将点P的坐标代入y=2x﹣1得,2=2m﹣1,解得m=1.5,故点P(1.5,2),
从图象看,当x≤1.5时,kx+b≥2x﹣1,故答案为:≤1.5;
(2)从图象看,不等式kx+b<0的解集是x>4,故答案为x>
(3)∵直线l2:y=2x﹣1交y轴于点A,故点A(0,﹣1),
设点H(s,t),
①当AB是边时,
点A向右平移4个单位向上平移1个单位得到点B,同样点P(H)向右平移4个单位向上平移1个单位得到H(P),
则1.5±4=s且2±1=t,解得,
故点H的坐标为(5.5,3)或(﹣2.5,1);
②当AB是对角线时,
由中点公式得:(0+4)=(s+1.5)且(﹣1+0)=(t+2),解得,
故点H的坐标为(2.5,﹣3).
综上,点H的坐标为(5.5,3)或(﹣2.5,1)或(2.5,﹣3).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
