华东师大版七上数学2.9.2有理数乘法的运算律课件(共17张PPT)
文档属性
| 名称 | 华东师大版七上数学2.9.2有理数乘法的运算律课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 973.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
2、计算:
1、有理数的乘法法则:
两数相乘,同号______,异号_______,
并把___________。任何数与0相乘,积________.
(1)(-2.5)
×4
(2)(-2005)
×0
(3)(-2.25)×(-3)
(4)3.5×
=
-
10
=
0
=
6.75
=
1
一、复习
得正
得负
绝对值相乘
仍为0
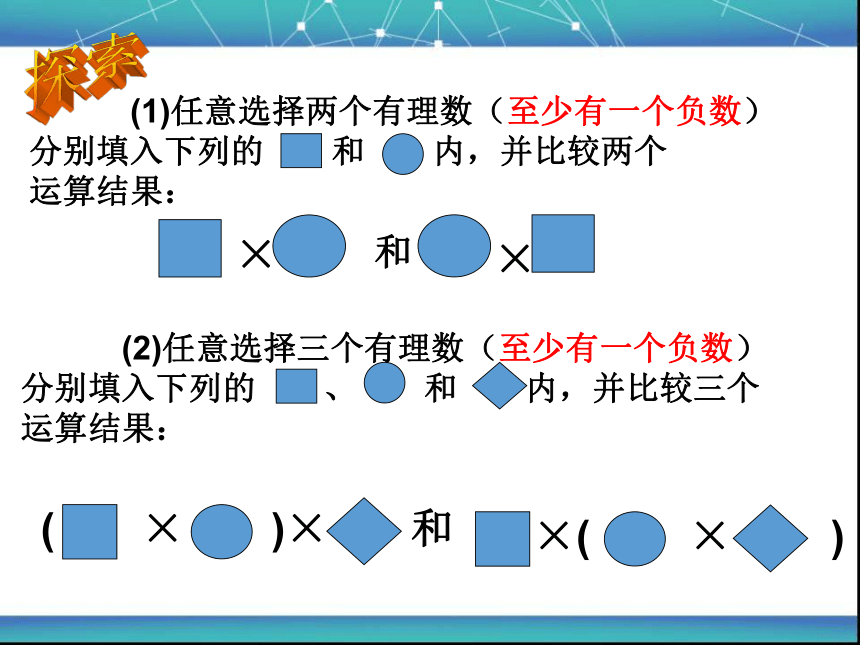
(1)任意选择两个有理数(至少有一个负数)
分别填入下列的 和 内,并比较两个
运算结果:
×
×
和
( × )×
×(
×
)
和
(2)任意选择三个有理数(至少有一个负数)
分别填入下列的 、 和 内,并比较三个
运算结果:
两个数相乘,交换两个因数的位置,积不变.
乘法交换律:ab
=
ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变.
乘法结合律:(ab)c
=
a(bc).
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,
也可先把其中的几个数相乘.
有理数乘法运算律:
[(-2)×5]
×(-
3
)
(-2)
×[5×(-3)]
=(-10)×(-3)
=
30
=
(-2)×(-15)
=
30
[(-2)×(
-3)]
×5
=
30
=
6×5
计算(-2)×5
×(-3)
例1.计算
解:
例题示范,初步运用
从上面的计算
得到什么结论?
试直接写出下列各式的结果:
2
-2
2
几个不是0的数相乘,负因数的个数是________时,积是负数;负因数的个数是________时,积是正数.
偶数
奇数
奇负偶正
例2.计算
解:
例题示范,初步运用
多个不是0的数相乘,,先做哪一步,再做哪一步?
多个不是0的数相乘,
先确定积的符号,再把各个因数的绝对值相乘。
几个数相乘,有一个因数为0,积就为0.
算一算,想一想
1.有一个因数为0,积就为0.
2.多个不是0的数相乘,
先确定积的符号,再把各个因数的绝对值相乘。
多个有理数相乘:
练习1、用“>”、“<”或“=”填空。
(1)(-3)×(-5)
×(-7)
×(-9) 0
(2)(+8.36)
×(+2.9)
×(-7.89) 0
(3)50
×(-2)
×(-3)
×(-2)
×(-5) 0
(4)(-3)
×(-2)
×(-1) 0
(5)739
×(-123)
×(-329)
×0 0
>
<
>
=
<
解(1)(1)1)
例2:计算
第二步:确定积的符号:奇负偶正;
第三步:绝对值相乘。结果记得检查符号
多个有理数相乘,
先做哪一步,再做哪一步?
第一步:乘数中是否有0。
1.乘法的交换律
2.乘法的结合律
3.几个不等于零的有理数相乘积的符号与负因数个数的关系(奇负偶正)
4.几个数和零相乘结果仍得零
本节课里我的收获是……
1.用“<”或“>”号填空
(1)如果a<0
b>0那么
ab
_
0
(2)如果a<0
b<0那么
ab
_
0
<
>
2.判断下列方程的解是正数、负数还是0:
(1)
4X=
-16
(2)-3X=18
(3)-9X=-36
(4)-5X=0
3.思考题:
(1)当a
>0时,a与
2a哪个大?
(2)当a
<
0时,a与2a哪个大?
2、计算:
1、有理数的乘法法则:
两数相乘,同号______,异号_______,
并把___________。任何数与0相乘,积________.
(1)(-2.5)
×4
(2)(-2005)
×0
(3)(-2.25)×(-3)
(4)3.5×
=
-
10
=
0
=
6.75
=
1
一、复习
得正
得负
绝对值相乘
仍为0
(1)任意选择两个有理数(至少有一个负数)
分别填入下列的 和 内,并比较两个
运算结果:
×
×
和
( × )×
×(
×
)
和
(2)任意选择三个有理数(至少有一个负数)
分别填入下列的 、 和 内,并比较三个
运算结果:
两个数相乘,交换两个因数的位置,积不变.
乘法交换律:ab
=
ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变.
乘法结合律:(ab)c
=
a(bc).
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,
也可先把其中的几个数相乘.
有理数乘法运算律:
[(-2)×5]
×(-
3
)
(-2)
×[5×(-3)]
=(-10)×(-3)
=
30
=
(-2)×(-15)
=
30
[(-2)×(
-3)]
×5
=
30
=
6×5
计算(-2)×5
×(-3)
例1.计算
解:
例题示范,初步运用
从上面的计算
得到什么结论?
试直接写出下列各式的结果:
2
-2
2
几个不是0的数相乘,负因数的个数是________时,积是负数;负因数的个数是________时,积是正数.
偶数
奇数
奇负偶正
例2.计算
解:
例题示范,初步运用
多个不是0的数相乘,,先做哪一步,再做哪一步?
多个不是0的数相乘,
先确定积的符号,再把各个因数的绝对值相乘。
几个数相乘,有一个因数为0,积就为0.
算一算,想一想
1.有一个因数为0,积就为0.
2.多个不是0的数相乘,
先确定积的符号,再把各个因数的绝对值相乘。
多个有理数相乘:
练习1、用“>”、“<”或“=”填空。
(1)(-3)×(-5)
×(-7)
×(-9) 0
(2)(+8.36)
×(+2.9)
×(-7.89) 0
(3)50
×(-2)
×(-3)
×(-2)
×(-5) 0
(4)(-3)
×(-2)
×(-1) 0
(5)739
×(-123)
×(-329)
×0 0
>
<
>
=
<
解(1)(1)1)
例2:计算
第二步:确定积的符号:奇负偶正;
第三步:绝对值相乘。结果记得检查符号
多个有理数相乘,
先做哪一步,再做哪一步?
第一步:乘数中是否有0。
1.乘法的交换律
2.乘法的结合律
3.几个不等于零的有理数相乘积的符号与负因数个数的关系(奇负偶正)
4.几个数和零相乘结果仍得零
本节课里我的收获是……
1.用“<”或“>”号填空
(1)如果a<0
b>0那么
ab
_
0
(2)如果a<0
b<0那么
ab
_
0
<
>
2.判断下列方程的解是正数、负数还是0:
(1)
4X=
-16
(2)-3X=18
(3)-9X=-36
(4)-5X=0
3.思考题:
(1)当a
>0时,a与
2a哪个大?
(2)当a
<
0时,a与2a哪个大?
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
