人教版数学九年级上册24.3正多边形的有关计算教案(表格式)
文档属性
| 名称 | 人教版数学九年级上册24.3正多边形的有关计算教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 168.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 23:15:13 | ||
图片预览

文档简介
课题
正多边形的有关计算
课时
1课时
课型
新授课
授课人
目标确定依据
课标要求
理解正多边形的有关概念及正多边形和圆的关系;掌握正多边形的有关计算方法。
教材分析
正多边形是和圆是在学生学习了三角形、四边形、多边形以及圆的相关知识后的内容,是前一阶段知识的运用和提高。正多边形是一种特殊的多边形,它有一些类似于圆的特性;研究正多边形和圆的关系,掌握有关正多边形的计算是进一步学习数学及其它学科的重要基础。
学情分析
学生已经学习了多边形的有关概念,圆的有关概念等等,有了一定的知识储备和方法准备,但处理正多边形与圆的有关计算时,要用到构造直角三角形的重要辅助线,对一些学生可能会有一定的思维障碍,在教学中应该充分认识到这一点并加以突破。
学习目标
1.理解正多边形的中心、半径、边心距、中心角等概念。2.能运用正多边形的知识解决与圆的有关计算问题。
重点难点
重点:了解正多边形的有关概念;理解正多边形和圆的关系;掌握有关正多边形的计算方法。难点:对正多边形和圆的关系的理解及正多边形相关概念计算的准确性。
学习过程学习过程
【知识链接】1.各边
,各角也
的多边形叫做正多边形.2.
如果一个多边形的
顶点都在
圆上,这个多边形叫做圆的内接多边形,这个圆叫做这个多边形的
。
.【自主学习】1.
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的______正多边形,这个圆就是这个正多边形的______圆.将一个圆五等分,依次连接各分点得到一个五边形,这五边形一定是正五边形吗?如果是请你证明这个结论.2.
正多边形的有关概念:一个正多边形的______________叫做这个正多边形的中心;______________叫正多边形的半径;正多边形每一边所对的______
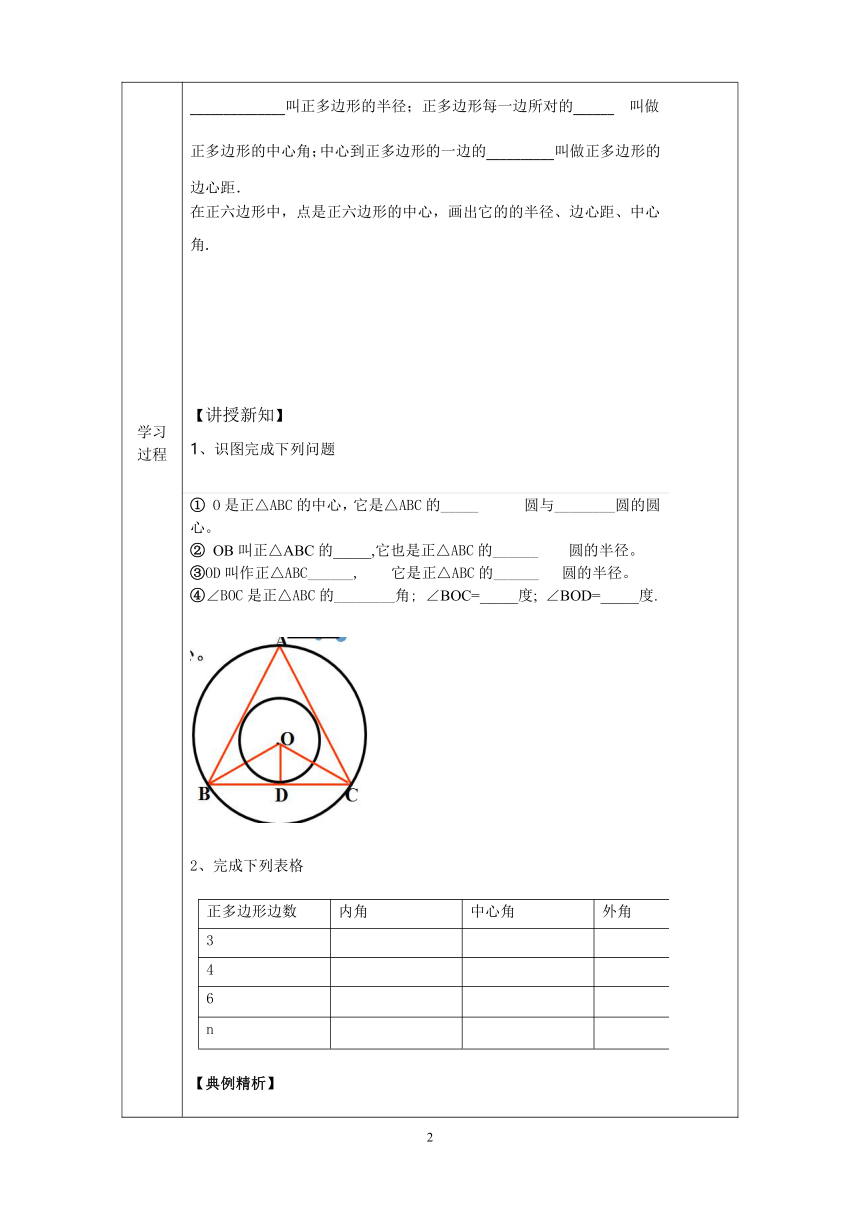
叫做正多边形的中心角;中心到正多边形的一边的__________叫做正多边形的边心距.在正六边形中,点是正六边形的中心,画出它的的半径、边心距、中心角.【讲授新知】1、识图完成下列问题①
O是正△ABC的中心,它是△ABC的_____
圆与________圆的圆心。②
OB叫正△ABC的_____,它也是正△ABC的______
圆的半径。③OD叫作正△ABC______,
它是正△ABC的______
圆的半径。④∠BOC是正△ABC的________角;
∠BOC=_____度;
∠BOD=_____度.2、完成下列表格正多边形边数内角中心角外角346n【典例精析】例1:有一个亭子,它的地基是半径为4
m的正六边形,求地基的周长和面积
(精确到0.1
m2).【巩固练习】1、如图所示,正五边形ABCDE内接于⊙O,则∠ADE的度数是(
)A.60°
B.45°
C.
36°
D.
30°
2.分别求出半径为R的圆内接正三角形,正方形的边长,边心距(内切圆的半径)和面积.
课堂小结
通过本节课的学习,你有那些收获?
测评反馈
1、如图,已知半径为4的圆内接正六边形ABCDEF:
①它的中心角等于
度
;
②
OC
BC
(填>、<或=);
③△OBC是
三角形;
④圆内接正六边形的面积是△OBC面积的
倍.
⑤圆内接正n边形面积公式:_______________________.2、若正多边形的边心距与半径的比为1:2,则这个多边形的边数是
.
3.
要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
4.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
课后反思
正多边形的有关计算
课时
1课时
课型
新授课
授课人
目标确定依据
课标要求
理解正多边形的有关概念及正多边形和圆的关系;掌握正多边形的有关计算方法。
教材分析
正多边形是和圆是在学生学习了三角形、四边形、多边形以及圆的相关知识后的内容,是前一阶段知识的运用和提高。正多边形是一种特殊的多边形,它有一些类似于圆的特性;研究正多边形和圆的关系,掌握有关正多边形的计算是进一步学习数学及其它学科的重要基础。
学情分析
学生已经学习了多边形的有关概念,圆的有关概念等等,有了一定的知识储备和方法准备,但处理正多边形与圆的有关计算时,要用到构造直角三角形的重要辅助线,对一些学生可能会有一定的思维障碍,在教学中应该充分认识到这一点并加以突破。
学习目标
1.理解正多边形的中心、半径、边心距、中心角等概念。2.能运用正多边形的知识解决与圆的有关计算问题。
重点难点
重点:了解正多边形的有关概念;理解正多边形和圆的关系;掌握有关正多边形的计算方法。难点:对正多边形和圆的关系的理解及正多边形相关概念计算的准确性。
学习过程学习过程
【知识链接】1.各边
,各角也
的多边形叫做正多边形.2.
如果一个多边形的
顶点都在
圆上,这个多边形叫做圆的内接多边形,这个圆叫做这个多边形的
。
.【自主学习】1.
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的______正多边形,这个圆就是这个正多边形的______圆.将一个圆五等分,依次连接各分点得到一个五边形,这五边形一定是正五边形吗?如果是请你证明这个结论.2.
正多边形的有关概念:一个正多边形的______________叫做这个正多边形的中心;______________叫正多边形的半径;正多边形每一边所对的______
叫做正多边形的中心角;中心到正多边形的一边的__________叫做正多边形的边心距.在正六边形中,点是正六边形的中心,画出它的的半径、边心距、中心角.【讲授新知】1、识图完成下列问题①
O是正△ABC的中心,它是△ABC的_____
圆与________圆的圆心。②
OB叫正△ABC的_____,它也是正△ABC的______
圆的半径。③OD叫作正△ABC______,
它是正△ABC的______
圆的半径。④∠BOC是正△ABC的________角;
∠BOC=_____度;
∠BOD=_____度.2、完成下列表格正多边形边数内角中心角外角346n【典例精析】例1:有一个亭子,它的地基是半径为4
m的正六边形,求地基的周长和面积
(精确到0.1
m2).【巩固练习】1、如图所示,正五边形ABCDE内接于⊙O,则∠ADE的度数是(
)A.60°
B.45°
C.
36°
D.
30°
2.分别求出半径为R的圆内接正三角形,正方形的边长,边心距(内切圆的半径)和面积.
课堂小结
通过本节课的学习,你有那些收获?
测评反馈
1、如图,已知半径为4的圆内接正六边形ABCDEF:
①它的中心角等于
度
;
②
OC
BC
(填>、<或=);
③△OBC是
三角形;
④圆内接正六边形的面积是△OBC面积的
倍.
⑤圆内接正n边形面积公式:_______________________.2、若正多边形的边心距与半径的比为1:2,则这个多边形的边数是
.
3.
要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
4.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
课后反思
同课章节目录
