22.2.1 平行线与相似三角形 沪科版九年级数学上册课时作业(含答案)
文档属性
| 名称 | 22.2.1 平行线与相似三角形 沪科版九年级数学上册课时作业(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 371.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
沪科版九年级数学上册课时作业
第22章 相似形
22.2 相似三角形的判定
第1课时 平行线与相似三角形
1.
下列说法正确的是
(
)
A.
相似三角形一定全等
B.
不相似的三角形不一定全等
C.
全等三角形不一定是相似三角形
D.
全等三角形一定是相似三角形
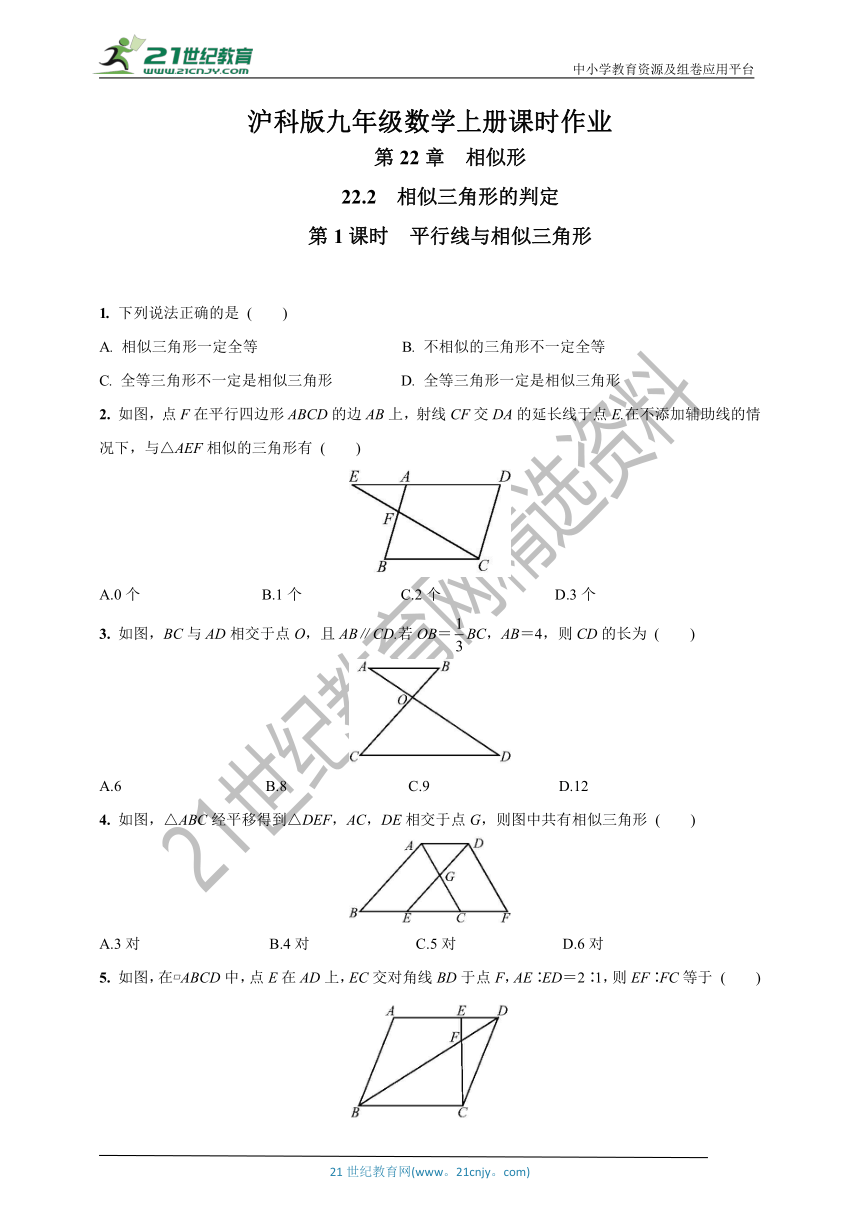
2.
如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E.在不添加辅助线的情况下,与△AEF相似的三角形有
(
)
A.0个
B.1个
C.2个
D.3个
3.
如图,BC与AD相交于点O,且AB∥CD.若OB=BC,AB=4,则CD的长为
(
)
A.6
B.8
C.9
D.12
4.
如图,△ABC经平移得到△DEF,AC,DE相交于点G,则图中共有相似三角形
(
)
A.3对
B.4对
C.5对
D.6对
5.
如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE∶ED=2∶1,则EF∶FC等于
(
)
A.1∶1
B.1∶2
C.1∶3
D.2∶3
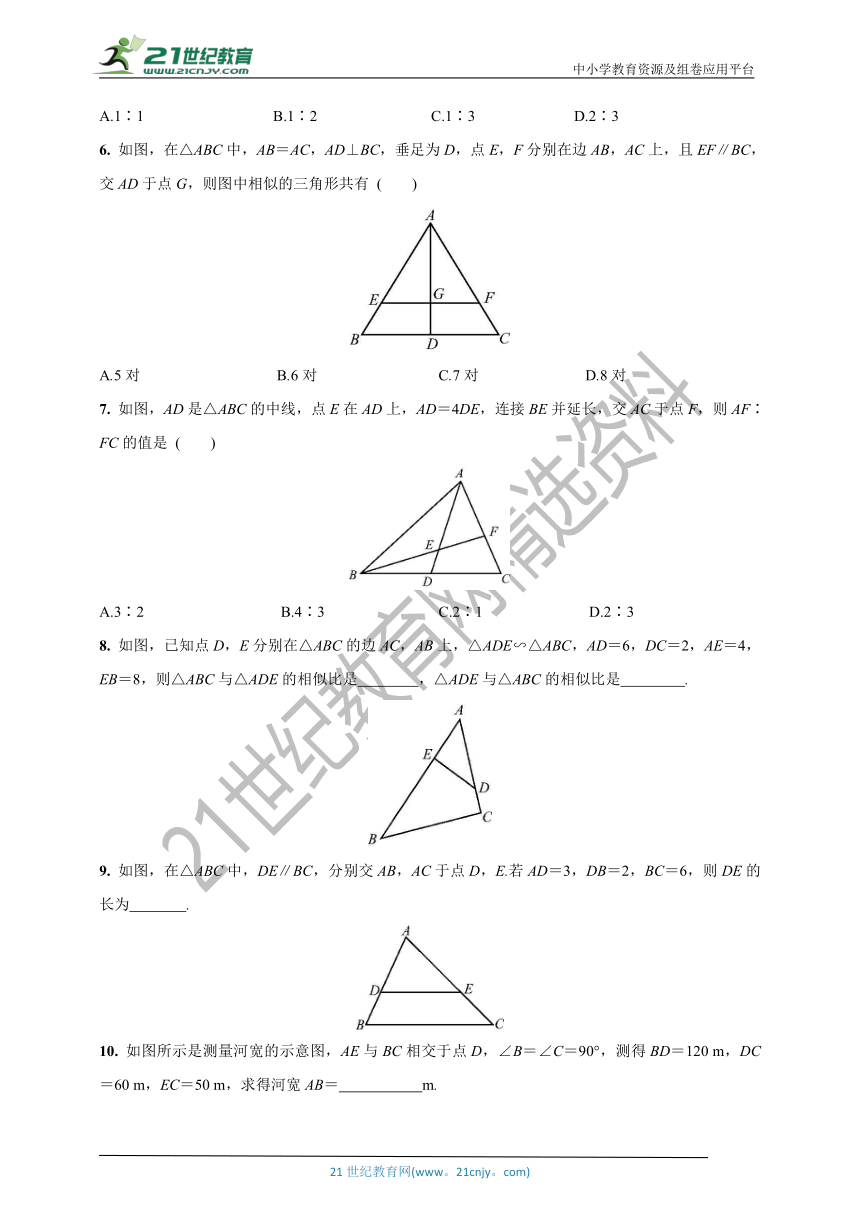
6.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E,F分别在边AB,AC上,且EF∥BC,交AD于点G,则图中相似的三角形共有
(
)
A.5对
B.6对
C.7对
D.8对
7.
如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长,交AC于点F,则AF∶FC的值是
(
)
A.3∶2
B.4∶3
C.2∶1
D.2∶3
8.
如图,已知点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,AD=6,DC=2,AE=4,EB=8,则△ABC与△ADE的相似比是
,△ADE与△ABC的相似比是?
.?
9.
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=3,DB=2,BC=6,则DE的长为?
.?
10.
如图所示是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120
m,DC=60
m,EC=50
m,求得河宽AB=
m.?
11.
如图,已知AB∥GH∥CD,点H在BC上,AC与BD相交于点G.若AB=2,CD=3,则GH的长为?
.?
12.
如图,在△ABC中,FG∥DE∥BC,且BD=DF=FA.求证:DE+FG=BC.
13.
如图,过△ABC的边BC的中点D任作一条直线交AC于点Q,交AB的延长线于点P,作AE∥BC交DQ的延长线于点E.
求证:PD·EQ=DQ·PE.
14.
如图,点M,N分别在△ABC的边AB,AC上,MN∥BC.过顶点A作BC的平行线PQ分别交CM和BN的延长线于点P和点Q.试判断线段AP与AQ之间的数量关系,并说明理由.
参
考
答
案
1.
D
2.
C
3.
B
4.
D
5.
C
6.
C
7.
A
8.
2
9.
10.
100
11.
12.
证明:∵FG∥BC,∴△AFG∽△ABC,∴=.
又∵BD=DF=AF,∴=,即FG=BC.
∵DE∥BC,∴==,即DE=BC,∴DE+FG=BC+BC=BC.
13.
证明:∵AE∥BC,∴△PBD∽△PAE,△DCQ∽△EAQ,∴=,=.
∵D为BC的中点,∴BD=CD,∴=,∴PD·EQ=DQ·PE.
14.
解:AP=AQ.
理由:∵MN∥BC,PQ∥BC,∴PQ∥MN∥BC,∴=.
∵MN∥AQ,∴△BMN∽△BAQ,∴=,同理=,∴=,∴AP=AQ.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www。21cnjy。com)
沪科版九年级数学上册课时作业
第22章 相似形
22.2 相似三角形的判定
第1课时 平行线与相似三角形
1.
下列说法正确的是
(
)
A.
相似三角形一定全等
B.
不相似的三角形不一定全等
C.
全等三角形不一定是相似三角形
D.
全等三角形一定是相似三角形
2.
如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E.在不添加辅助线的情况下,与△AEF相似的三角形有
(
)
A.0个
B.1个
C.2个
D.3个
3.
如图,BC与AD相交于点O,且AB∥CD.若OB=BC,AB=4,则CD的长为
(
)
A.6
B.8
C.9
D.12
4.
如图,△ABC经平移得到△DEF,AC,DE相交于点G,则图中共有相似三角形
(
)
A.3对
B.4对
C.5对
D.6对
5.
如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE∶ED=2∶1,则EF∶FC等于
(
)
A.1∶1
B.1∶2
C.1∶3
D.2∶3
6.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E,F分别在边AB,AC上,且EF∥BC,交AD于点G,则图中相似的三角形共有
(
)
A.5对
B.6对
C.7对
D.8对
7.
如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长,交AC于点F,则AF∶FC的值是
(
)
A.3∶2
B.4∶3
C.2∶1
D.2∶3
8.
如图,已知点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,AD=6,DC=2,AE=4,EB=8,则△ABC与△ADE的相似比是
,△ADE与△ABC的相似比是?
.?
9.
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=3,DB=2,BC=6,则DE的长为?
.?
10.
如图所示是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120
m,DC=60
m,EC=50
m,求得河宽AB=
m.?
11.
如图,已知AB∥GH∥CD,点H在BC上,AC与BD相交于点G.若AB=2,CD=3,则GH的长为?
.?
12.
如图,在△ABC中,FG∥DE∥BC,且BD=DF=FA.求证:DE+FG=BC.
13.
如图,过△ABC的边BC的中点D任作一条直线交AC于点Q,交AB的延长线于点P,作AE∥BC交DQ的延长线于点E.
求证:PD·EQ=DQ·PE.
14.
如图,点M,N分别在△ABC的边AB,AC上,MN∥BC.过顶点A作BC的平行线PQ分别交CM和BN的延长线于点P和点Q.试判断线段AP与AQ之间的数量关系,并说明理由.
参
考
答
案
1.
D
2.
C
3.
B
4.
D
5.
C
6.
C
7.
A
8.
2
9.
10.
100
11.
12.
证明:∵FG∥BC,∴△AFG∽△ABC,∴=.
又∵BD=DF=AF,∴=,即FG=BC.
∵DE∥BC,∴==,即DE=BC,∴DE+FG=BC+BC=BC.
13.
证明:∵AE∥BC,∴△PBD∽△PAE,△DCQ∽△EAQ,∴=,=.
∵D为BC的中点,∴BD=CD,∴=,∴PD·EQ=DQ·PE.
14.
解:AP=AQ.
理由:∵MN∥BC,PQ∥BC,∴PQ∥MN∥BC,∴=.
∵MN∥AQ,∴△BMN∽△BAQ,∴=,同理=,∴=,∴AP=AQ.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www。21cnjy。com)
