山东省潍坊市安丘市2020-2021学年七年级下学期期末数学试卷(Word版 含解析)
文档属性
| 名称 | 山东省潍坊市安丘市2020-2021学年七年级下学期期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 229.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 00:00:00 | ||
图片预览



文档简介
2020-2021学年山东省潍坊市安丘市七年级(下)期末数学试卷
一、单项选择题(每小题3分,共24分.每小题给出的4个选项中,只有一个选项是正确的)
1.一个角的度数为51°14'36″,则这个角的余角为( )
A.38°45′24″
B.39°45'24″
C.38°46′24″
D.39°46′24″
2.下列运算正确的是( )
A.a3+a2=a5
B.2a(1﹣a)=2a﹣2a2
C.(﹣ab2)3=a3b6
D.(a+b)2=a2+b2
3.用下列一种正多边形可以拼地板的是( )
A.正五边形
B.正六边形
C.正八边形
D.正十二边形
4.点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴的坐标是( )
A.(8,0)
B.(0,﹣8)
C.(0,8)
D.(﹣8,0)
5.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为( )
A.
B.
C.
D.
6.已知x2+y2+2x﹣6y+10=0,则x+y=( )
A.2
B.﹣2
C.4
D.﹣4
7.如图是小刚的一张脸,他对妹妹说“如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
A.(1,0)
B.(﹣1,0)
C.(﹣1,1)
D.(1,﹣1)
8.计算(2+1)(22+1)(24+1)…(232+1)的结果为( )
A.235+2
B.264+1
C.264﹣1
D.232﹣1
二、多项选择题(每小题3分,共12分.每小题给出的4个选项中,有多选项是符合题目要求,全对的的3分,部分选对的的2分,有选错的的0分)
9.下面计算正确的是
.
A.(﹣0.2)0=1
B.(﹣0.1)﹣3=﹣
C.30÷3﹣1=3
D.a4÷a4=a(a≠0)
10.在自习课上,小红为了检测同学们的学习效果,提出如下四种说法,其中错误的说法是
.
A.三角形有且只有一条中线;
B.三角形的高一定在三角形内部;
C.三角形的两边之差大于第三边;
D.三角形按边分类可分为等腰三角形和不等边三角形.
11.下列从左到右的变形,是因式分解的是
.
A.x2﹣9=(x+3)(x﹣3)
B.(y+1)(y﹣3)=(3﹣y)(y+1)
C.4yz﹣2y2z+z=2y(2z﹣zy)+z
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2
12.如图,其中能判断直线l1∥l2的条件有
.
A.∠4=∠5
B.∠2+∠5=180°
C.∠1=∠3
D.∠6=∠1+∠2
三、填空题(本题共8小题,共24分,只要求填写最后结果,每小题填对得3分)
13.若一个多边形的内角和为1080°,则这个多边形
边形.
14.(x+2)(2x﹣3)=2x2+mx﹣6,则m=
.
15.学校位于小亮家北偏东35°方向,距离为300m,学校位于大刚家南偏东85°方向,距离也为300m,则大刚家相对与小亮家的位置是
.
16.计算=
.
17.如果P(m+3,2m+4)在y轴上,那么点P的坐标是
.
18.若关于x,y的二元一次方程组的解也是二元一次方程x﹣3y=6的解,则k=
.
19.若多项式x2﹣(k+1)x+9是完全平方式,则k=
.
20.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式
.
四、解答题(本大题共7小题,共计60分)
21.(12分)计算:
(1)(2a)3﹣3a5÷a2;
(2)(x2y﹣2xy+y2)?(﹣4xy).
因式分解:
(3)x3﹣6x2+9x;
(4)a2(x﹣y)﹣9(x﹣y).
22.(8分)解下列方程组:
(1);
(2);
23.(6分)如图,直线a∥b,直线AB与直线a,b分别相交于点A、B,AC交直线b于点C.
(1)若AC⊥AB,∠1=54°49′.求∠2的度数;
(2)请说明∠ABC+∠BCA+∠CAB=180°.
24.(6分)观察下面的4个等式:
22﹣12=3,32﹣22=5,42﹣32=7,52﹣42=9.
(1)请你写出第5个等式
;
(2)用含字母n的等式表示你发现的规律,并用学过的知识说明规律的正确性.
25.(8分)2020年疫情期间,山东省按“一省包一市”的方式,全力支援湖北省黄冈市,截止到2020年2月7日24时,共有确诊病例2044例,每六名轻症患者需要一名医护工作者.一名重症患者需要一名医护工作者,山东省共派去574名医护人员.请问轻症病人和重症病人各有多少名?
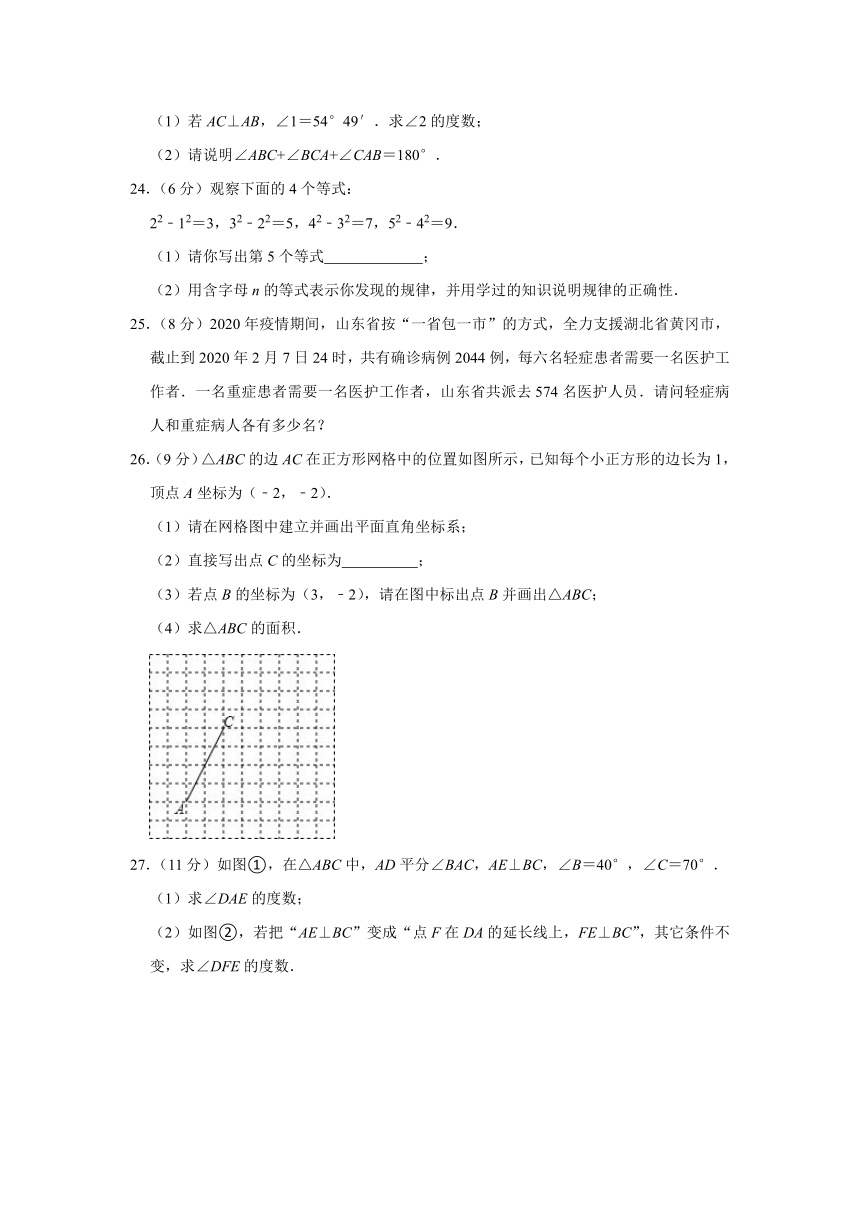
26.(9分)△ABC的边AC在正方形网格中的位置如图所示,已知每个小正方形的边长为1,顶点A坐标为(﹣2,﹣2).
(1)请在网格图中建立并画出平面直角坐标系;
(2)直接写出点C的坐标为
;
(3)若点B的坐标为(3,﹣2),请在图中标出点B并画出△ABC;
(4)求△ABC的面积.
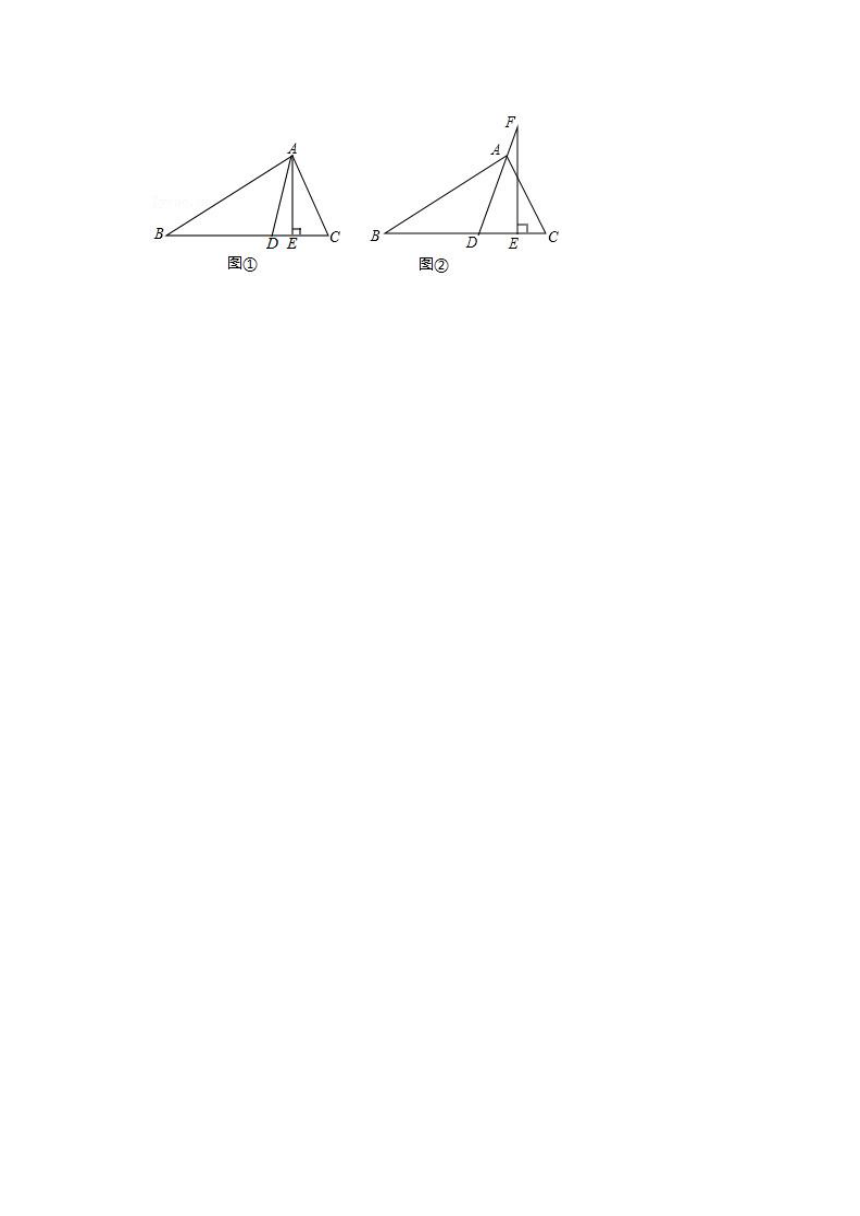
27.(11分)如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
2020-2021学年山东省潍坊市安丘市七年级(下)期末数学试卷
参考答案与试题解析
一、单项选择题(每小题3分,共24分.每小题给出的4个选项中,只有一个选项是正确的)
1.一个角的度数为51°14'36″,则这个角的余角为( )
A.38°45′24″
B.39°45'24″
C.38°46′24″
D.39°46′24″
【分析】依据余角的定义求解即可.
【解答】解:这个角的余角=90°﹣51°14'36″=89°60′﹣51°14'36″=38°45′24″.
故选:A.
2.下列运算正确的是( )
A.a3+a2=a5
B.2a(1﹣a)=2a﹣2a2
C.(﹣ab2)3=a3b6
D.(a+b)2=a2+b2
【分析】直接利用合并同类项法则、积的乘方运算法则以及单项式乘多项式运算法则、完全平方公式分别计算得出答案.
【解答】解:A.a3+a2无法计算,故此选项不合题意;
B.2a(1﹣a)=2a﹣2a2,故此选项符合题意;
C.(﹣ab2)3=﹣a3b6,故此选项不合题意;
D.(a+b)2=a2+2ab+b2,故此选项不合题意;
故选:B.
3.用下列一种正多边形可以拼地板的是( )
A.正五边形
B.正六边形
C.正八边形
D.正十二边形
【分析】先计算各正多边形每一个内角的度数,判断是否为360°的约数.
【解答】解:A、正五边形的每一个内角度数为180°﹣360°÷5=108°,108°不是360°的约数,故一种正五边形不能拼地板;
B、正六边形的每一个内角度数为180°﹣360°÷6=120°,120°是360°的约数,故一种六边形能拼地板;
C、正八边形的每一个内角度数为180°﹣360°÷8=135°,135°不是360°的约数,故一种正八边形不能拼地板;
D、正十二边形的每一个内角度数为180°﹣360°÷12=150°,150°不是360°的约数,故一种正十二边形不能拼地板;
故选:B.
4.点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴的坐标是( )
A.(8,0)
B.(0,﹣8)
C.(0,8)
D.(﹣8,0)
【分析】首先根据点A(0,﹣3),以A为圆心,5为半径画圆,可得出圆与y轴负半轴的交点,即可得出答案.
【解答】解:∵点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴,
∴A为圆心,5为半径画圆交y轴负半轴的长度是:3+5=8,
故坐标为:(0,﹣8),
故选:B.
5.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为( )
A.
B.
C.
D.
【分析】根据题意中的两种分法,分别找到等量关系:
①组数×每组7人=总人数﹣3人;②组数×每组8人=总人数+5人.
【解答】解:根据组数×每组7人=总人数﹣3人,得方程7y=x﹣3;根据组数×每组8人=总人数+5人,得方程8y=x+5.
列方程组为.
故选:C.
6.已知x2+y2+2x﹣6y+10=0,则x+y=( )
A.2
B.﹣2
C.4
D.﹣4
【分析】将原式的左边利用分组分解法分解后分别求得x和y的值后代入即可求解.
【解答】解:∵x2+y2+2x﹣6y+10=0,
∴x2+2x+1+y2﹣6y+9=0
即:(x+1)2+(y﹣3)2=0
解得:x=﹣1,y=3
∴x+y=﹣1+3=2,
故选:A.
7.如图是小刚的一张脸,他对妹妹说“如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
A.(1,0)
B.(﹣1,0)
C.(﹣1,1)
D.(1,﹣1)
【分析】由“左眼”位置点的坐标为(0,2),“右眼”点的坐标为(2,2)可以确定平面直角坐标系中x轴与y轴的位置,从而可以确定“嘴”的坐标.
【解答】解:根据题意,坐标原点是嘴所在的行和左眼所在的列的位置,所以嘴的坐标是(1,0),故选A.
8.计算(2+1)(22+1)(24+1)…(232+1)的结果为( )
A.235+2
B.264+1
C.264﹣1
D.232﹣1
【分析】把前面的1变为(2﹣1),再依次运用平方差公式进行计算即可.
【解答】解:原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1),
=(22﹣1)(22+1)(24+1)(28+1)(216+1)(232+1),
=(24﹣1)(24+1)(28+1)(216+1)(232+1),
=(28﹣1)(28+1)(216+1)(232+1),
=(216﹣1)(216+1)(232+1),
=(232﹣1)(232+1),
=264﹣1
故选:C.
二、多项选择题(每小题3分,共12分.每小题给出的4个选项中,有多选项是符合题目要求,全对的的3分,部分选对的的2分,有选错的的0分)
9.下面计算正确的是
AC .
A.(﹣0.2)0=1
B.(﹣0.1)﹣3=﹣
C.30÷3﹣1=3
D.a4÷a4=a(a≠0)
【分析】根据零指数幂对A选项进行判断;根据负整数指数幂的意义对B选项进行判断;利用零指数幂与负整数指数幂的意义对C进行判断;根据同底数幂的除法法则对D进行判断.
【解答】解:A.(﹣0.2)0=1,所以A选项符合题意;
B.(﹣0.1)﹣3==﹣1000,所以B选项不符合题意;
C.30÷3﹣1=1÷=1×3=3,所以C选项符合题意;
A.a4÷a4=a0=1(a≠0),所以D选项不符合题意.
故答案为AC.
10.在自习课上,小红为了检测同学们的学习效果,提出如下四种说法,其中错误的说法是
ABC .
A.三角形有且只有一条中线;
B.三角形的高一定在三角形内部;
C.三角形的两边之差大于第三边;
D.三角形按边分类可分为等腰三角形和不等边三角形.
【分析】根据三角形的分类、三角形的三边关系进行判断.
【解答】解:A.三角形有3条中线,原来的说法是错误的;
B.三角形的高不一定在三角形内部,原来的说法是错误的;
C.三角形的两边之差小于第三边,原来的说法是错误的;
D.三角形按边分类可分为等腰三角形和不等边三角形是正确的.
故答案为:ABC.
11.下列从左到右的变形,是因式分解的是
AD .
A.x2﹣9=(x+3)(x﹣3)
B.(y+1)(y﹣3)=(3﹣y)(y+1)
C.4yz﹣2y2z+z=2y(2z﹣zy)+z
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2
【分析】根据因式分解的定义,以及提公因式法和公式法进行判断求解.把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.
【解答】解:A.x2﹣9=(x+3)(x﹣3),把一个多项式化为几个整式的积的形式,是因式分解;
B.(y+1)(y﹣3)≠(3﹣y)(y+1);
C.4yz﹣2y2z+z=2y(2z﹣zy)+z,等式的右边不是几个整式的积的形式,不是因式分解;
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2,把一个多项式化为几个整式的积的形式,是因式分解;
故答案为:AD.
12.如图,其中能判断直线l1∥l2的条件有
ACD .
A.∠4=∠5
B.∠2+∠5=180°
C.∠1=∠3
D.∠6=∠1+∠2
【分析】平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;依此对各小题进行逐一判断即可.
【解答】解:①∵∠4=∠5,∴l1∥l2,故本条件符合题意;
②由∠2+∠5=180°不能得到l1∥l2,故本条件符合题意;
③∵∠1=∠3,∴l1∥l2,故本条件符合题意;
④∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件不合题意.
故答案为:ACD.
三、填空题(本题共8小题,共24分,只要求填写最后结果,每小题填对得3分)
13.若一个多边形的内角和为1080°,则这个多边形 8 边形.
【分析】首先设这个多边形的边数为n,由n边形的内角和等于180°(n﹣2),即可得方程180(n﹣2)=1080,解此方程即可求得答案.
【解答】解:设这个多边形的边数为n,
根据题意得:180(n﹣2)=1080,
解得:n=8,
故答案为:8.
14.(x+2)(2x﹣3)=2x2+mx﹣6,则m= 1 .
【分析】按照多项式乘以多项式把等式的左边展开,根据等式的左边等于右边,即可解答.
【解答】解:(x+2)(2x﹣3)=2x2﹣3x+4x﹣6=2x2+x﹣6=2x2+mx﹣6,
∴m=1,
故答案为:1.
15.学校位于小亮家北偏东35°方向,距离为300m,学校位于大刚家南偏东85°方向,距离也为300m,则大刚家相对与小亮家的位置是 北偏西25°方向,距离为300m .
【分析】由题意可知,小亮家、大刚家和学校构成了一个等边三角形,再根据“上北下南,左西右东“即可得出刚家相对与小亮家的位置.
【解答】解:据分析可知:小亮家、大刚家和学校构成了一个等边三角形,所以大刚家相对与小亮家的位置是北偏西25°方向,距离为300m.
故答案为北偏西25°方向,距离为300m.
16.计算= 2020 .
【分析】原式分母减数变形后,利用平方差公式计算即可求出值.
【解答】解:原式=
=
=
=2020.
故答案为:2020.
17.如果P(m+3,2m+4)在y轴上,那么点P的坐标是 (0,﹣2) .
【分析】点P在y轴上则该点横坐标为0,可解得m的值,从而得到点P的坐标.
【解答】解:∵P(m+3,2m+4)在y轴上,
∴m+3=0,得m=﹣3,
即2m+4=﹣2.即点P的坐标为(0,﹣2).
故答案为:(0,﹣2).
18.若关于x,y的二元一次方程组的解也是二元一次方程x﹣3y=6的解,则k= 1 .
【分析】把k看做已知数表示出方程组的解,代入已知方程求出k的值即可.
【解答】解:,
①+②得:2x=6k,即x=3k,
②﹣①得:2y=﹣2k,即y=﹣k,
把x=3k,y=﹣k代入x﹣3y=6中得:3k+3k=6,
解得:k=1,
故答案为:1
19.若多项式x2﹣(k+1)x+9是完全平方式,则k= 5或﹣7 .
【分析】利用完全平方公式的结构特征判断即可.
【解答】解:∵多项式x2﹣(k+1)x+9是完全平方式,
∴k+1=±6,
解得:k=5或﹣7,
故答案为:5或﹣7.
20.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式 a2﹣b2=(a+b)(a﹣b) .
【分析】左图中阴影部分的面积是a2﹣b2,右图中梯形的面积是(2a+2b)(a﹣b)=(a+b)(a﹣b),根据面积相等即可解答.
【解答】解:a2﹣b2=(a+b)(a﹣b).
四、解答题(本大题共7小题,共计60分)
21.(12分)计算:
(1)(2a)3﹣3a5÷a2;
(2)(x2y﹣2xy+y2)?(﹣4xy).
因式分解:
(3)x3﹣6x2+9x;
(4)a2(x﹣y)﹣9(x﹣y).
【分析】(1)利用积的乘方法则进行运算;
(2)利用单项式乘多项式法则进行运算;
(3)先提取公因式,再用完全平方公式进行分解;
(4)先提取公因式,再利用平方差公式因式分解.
【解答】解:(1)原式=8a3﹣3a3=5a3;
(2)原式=﹣2x3y2+8x2y2﹣4xy3;
(3)x3﹣6x2+9x
=x(x2﹣6x+9)
=x(x﹣3)2;
(4)a2(x﹣y)﹣9(x﹣y)
=(x﹣y)(a2﹣9)
=(x﹣y)(a+3)(a﹣3).
22.(8分)解下列方程组:
(1);
(2);
【分析】(1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
【解答】解:(1),
①×4+②×3得:25a=﹣25,
解得:a=﹣1,
把a=﹣1代入①得:b=0,
则方程组的解为;
(2)方程组整理得:,
①+②×3得:5x=﹣26,
解得:x=﹣5.2,
把x=﹣5.2代入②得:y=﹣4.8,
则方程组的解为.
23.(6分)如图,直线a∥b,直线AB与直线a,b分别相交于点A、B,AC交直线b于点C.
(1)若AC⊥AB,∠1=54°49′.求∠2的度数;
(2)请说明∠ABC+∠BCA+∠CAB=180°.
【分析】(1)依据直线a∥b,AC⊥AB,即可得到∠2=90°﹣∠3=35°11′;
(2)利用平行线的性质定理可得结论.
【解答】解:(1)如图,
∵直线a∥b,
∴∠3=∠1=54°49′,
又∵AC⊥AB,
∴∠2=90°﹣∠3=35°11′;
(2)∵a∥b,
∴∠ACB=∠3,
∠ABC=∠4,
∵∠4+∠3+∠BAC=180°,
∴∠ABC+∠BCA+∠CAB=180°.
24.(6分)观察下面的4个等式:
22﹣12=3,32﹣22=5,42﹣32=7,52﹣42=9.
(1)请你写出第5个等式 62﹣52=11 ;
(2)用含字母n的等式表示你发现的规律,并用学过的知识说明规律的正确性.
【分析】等式左边的底数为相邻的两个整数的平方差,右边是连续的奇数.
【解答】解:规律为:(n+1)2﹣n2=2n+1
因为,(n+1)2﹣n2=n2+2n+1﹣n2=2n+1
所以:(n+1)2﹣n2=2n+1
25.(8分)2020年疫情期间,山东省按“一省包一市”的方式,全力支援湖北省黄冈市,截止到2020年2月7日24时,共有确诊病例2044例,每六名轻症患者需要一名医护工作者.一名重症患者需要一名医护工作者,山东省共派去574名医护人员.请问轻症病人和重症病人各有多少名?
【分析】根据确诊病例数和医护人员数分别列方程,解方程即可求出轻症病人和重症病人各有多少名.
【解答】解:设轻症病人x人,重症病人y人,
根据题意得,
解得,
答:轻症病人有1764名,重症病人有280名.
26.(9分)△ABC的边AC在正方形网格中的位置如图所示,已知每个小正方形的边长为1,顶点A坐标为(﹣2,﹣2).
(1)请在网格图中建立并画出平面直角坐标系;
(2)直接写出点C的坐标为 (0,2) ;
(3)若点B的坐标为(3,﹣2),请在图中标出点B并画出△ABC;
(4)求△ABC的面积.
【分析】(1)根据点A的坐标建立平面直角坐标系;
(2)根据平面直角坐标系得到C的坐标;
(3)根据题意作出图形即可;
(4)根据A坐标为(﹣2,﹣2),C的坐标为(2,0),B的坐标为(3,﹣2),即可得到结论.
【解答】解:(1)如图所示;
(2)C的坐标为(0,2);
故答案为:(0,2);
(3)如图所示,△ABC即为所求;
(4)∵A坐标为(﹣2,﹣2),C的坐标为(2,0),B的坐标为(3,﹣2),∴S△ABC=×5×4=10.
27.(11分)如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
【分析】(1)先根据三角形内角和定理求出∠BAC的度数,再由角平分线的定义得出∠BAD的度数,再由AE⊥BC得出∠AEB=90°,进而可得出结论;
(2)同(1),可得∠ADE=75°,再由FE⊥BC可知∠FEB=90°,根据∠DFE=90°﹣∠ADE可得出结论.
【解答】解(1)∵∠B=40°,∠C=70°,
∴∠BAC=70°.
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°.
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°﹣∠ADE=15°;
(2)同(1),可得∠ADE=75°.
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°﹣∠ADE=15°.
一、单项选择题(每小题3分,共24分.每小题给出的4个选项中,只有一个选项是正确的)
1.一个角的度数为51°14'36″,则这个角的余角为( )
A.38°45′24″
B.39°45'24″
C.38°46′24″
D.39°46′24″
2.下列运算正确的是( )
A.a3+a2=a5
B.2a(1﹣a)=2a﹣2a2
C.(﹣ab2)3=a3b6
D.(a+b)2=a2+b2
3.用下列一种正多边形可以拼地板的是( )
A.正五边形
B.正六边形
C.正八边形
D.正十二边形
4.点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴的坐标是( )
A.(8,0)
B.(0,﹣8)
C.(0,8)
D.(﹣8,0)
5.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为( )
A.
B.
C.
D.
6.已知x2+y2+2x﹣6y+10=0,则x+y=( )
A.2
B.﹣2
C.4
D.﹣4
7.如图是小刚的一张脸,他对妹妹说“如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
A.(1,0)
B.(﹣1,0)
C.(﹣1,1)
D.(1,﹣1)
8.计算(2+1)(22+1)(24+1)…(232+1)的结果为( )
A.235+2
B.264+1
C.264﹣1
D.232﹣1
二、多项选择题(每小题3分,共12分.每小题给出的4个选项中,有多选项是符合题目要求,全对的的3分,部分选对的的2分,有选错的的0分)
9.下面计算正确的是
.
A.(﹣0.2)0=1
B.(﹣0.1)﹣3=﹣
C.30÷3﹣1=3
D.a4÷a4=a(a≠0)
10.在自习课上,小红为了检测同学们的学习效果,提出如下四种说法,其中错误的说法是
.
A.三角形有且只有一条中线;
B.三角形的高一定在三角形内部;
C.三角形的两边之差大于第三边;
D.三角形按边分类可分为等腰三角形和不等边三角形.
11.下列从左到右的变形,是因式分解的是
.
A.x2﹣9=(x+3)(x﹣3)
B.(y+1)(y﹣3)=(3﹣y)(y+1)
C.4yz﹣2y2z+z=2y(2z﹣zy)+z
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2
12.如图,其中能判断直线l1∥l2的条件有
.
A.∠4=∠5
B.∠2+∠5=180°
C.∠1=∠3
D.∠6=∠1+∠2
三、填空题(本题共8小题,共24分,只要求填写最后结果,每小题填对得3分)
13.若一个多边形的内角和为1080°,则这个多边形
边形.
14.(x+2)(2x﹣3)=2x2+mx﹣6,则m=
.
15.学校位于小亮家北偏东35°方向,距离为300m,学校位于大刚家南偏东85°方向,距离也为300m,则大刚家相对与小亮家的位置是
.
16.计算=
.
17.如果P(m+3,2m+4)在y轴上,那么点P的坐标是
.
18.若关于x,y的二元一次方程组的解也是二元一次方程x﹣3y=6的解,则k=
.
19.若多项式x2﹣(k+1)x+9是完全平方式,则k=
.
20.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式
.
四、解答题(本大题共7小题,共计60分)
21.(12分)计算:
(1)(2a)3﹣3a5÷a2;
(2)(x2y﹣2xy+y2)?(﹣4xy).
因式分解:
(3)x3﹣6x2+9x;
(4)a2(x﹣y)﹣9(x﹣y).
22.(8分)解下列方程组:
(1);
(2);
23.(6分)如图,直线a∥b,直线AB与直线a,b分别相交于点A、B,AC交直线b于点C.
(1)若AC⊥AB,∠1=54°49′.求∠2的度数;
(2)请说明∠ABC+∠BCA+∠CAB=180°.
24.(6分)观察下面的4个等式:
22﹣12=3,32﹣22=5,42﹣32=7,52﹣42=9.
(1)请你写出第5个等式
;
(2)用含字母n的等式表示你发现的规律,并用学过的知识说明规律的正确性.
25.(8分)2020年疫情期间,山东省按“一省包一市”的方式,全力支援湖北省黄冈市,截止到2020年2月7日24时,共有确诊病例2044例,每六名轻症患者需要一名医护工作者.一名重症患者需要一名医护工作者,山东省共派去574名医护人员.请问轻症病人和重症病人各有多少名?
26.(9分)△ABC的边AC在正方形网格中的位置如图所示,已知每个小正方形的边长为1,顶点A坐标为(﹣2,﹣2).
(1)请在网格图中建立并画出平面直角坐标系;
(2)直接写出点C的坐标为
;
(3)若点B的坐标为(3,﹣2),请在图中标出点B并画出△ABC;
(4)求△ABC的面积.
27.(11分)如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
2020-2021学年山东省潍坊市安丘市七年级(下)期末数学试卷
参考答案与试题解析
一、单项选择题(每小题3分,共24分.每小题给出的4个选项中,只有一个选项是正确的)
1.一个角的度数为51°14'36″,则这个角的余角为( )
A.38°45′24″
B.39°45'24″
C.38°46′24″
D.39°46′24″
【分析】依据余角的定义求解即可.
【解答】解:这个角的余角=90°﹣51°14'36″=89°60′﹣51°14'36″=38°45′24″.
故选:A.
2.下列运算正确的是( )
A.a3+a2=a5
B.2a(1﹣a)=2a﹣2a2
C.(﹣ab2)3=a3b6
D.(a+b)2=a2+b2
【分析】直接利用合并同类项法则、积的乘方运算法则以及单项式乘多项式运算法则、完全平方公式分别计算得出答案.
【解答】解:A.a3+a2无法计算,故此选项不合题意;
B.2a(1﹣a)=2a﹣2a2,故此选项符合题意;
C.(﹣ab2)3=﹣a3b6,故此选项不合题意;
D.(a+b)2=a2+2ab+b2,故此选项不合题意;
故选:B.
3.用下列一种正多边形可以拼地板的是( )
A.正五边形
B.正六边形
C.正八边形
D.正十二边形
【分析】先计算各正多边形每一个内角的度数,判断是否为360°的约数.
【解答】解:A、正五边形的每一个内角度数为180°﹣360°÷5=108°,108°不是360°的约数,故一种正五边形不能拼地板;
B、正六边形的每一个内角度数为180°﹣360°÷6=120°,120°是360°的约数,故一种六边形能拼地板;
C、正八边形的每一个内角度数为180°﹣360°÷8=135°,135°不是360°的约数,故一种正八边形不能拼地板;
D、正十二边形的每一个内角度数为180°﹣360°÷12=150°,150°不是360°的约数,故一种正十二边形不能拼地板;
故选:B.
4.点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴的坐标是( )
A.(8,0)
B.(0,﹣8)
C.(0,8)
D.(﹣8,0)
【分析】首先根据点A(0,﹣3),以A为圆心,5为半径画圆,可得出圆与y轴负半轴的交点,即可得出答案.
【解答】解:∵点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴,
∴A为圆心,5为半径画圆交y轴负半轴的长度是:3+5=8,
故坐标为:(0,﹣8),
故选:B.
5.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为( )
A.
B.
C.
D.
【分析】根据题意中的两种分法,分别找到等量关系:
①组数×每组7人=总人数﹣3人;②组数×每组8人=总人数+5人.
【解答】解:根据组数×每组7人=总人数﹣3人,得方程7y=x﹣3;根据组数×每组8人=总人数+5人,得方程8y=x+5.
列方程组为.
故选:C.
6.已知x2+y2+2x﹣6y+10=0,则x+y=( )
A.2
B.﹣2
C.4
D.﹣4
【分析】将原式的左边利用分组分解法分解后分别求得x和y的值后代入即可求解.
【解答】解:∵x2+y2+2x﹣6y+10=0,
∴x2+2x+1+y2﹣6y+9=0
即:(x+1)2+(y﹣3)2=0
解得:x=﹣1,y=3
∴x+y=﹣1+3=2,
故选:A.
7.如图是小刚的一张脸,他对妹妹说“如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
A.(1,0)
B.(﹣1,0)
C.(﹣1,1)
D.(1,﹣1)
【分析】由“左眼”位置点的坐标为(0,2),“右眼”点的坐标为(2,2)可以确定平面直角坐标系中x轴与y轴的位置,从而可以确定“嘴”的坐标.
【解答】解:根据题意,坐标原点是嘴所在的行和左眼所在的列的位置,所以嘴的坐标是(1,0),故选A.
8.计算(2+1)(22+1)(24+1)…(232+1)的结果为( )
A.235+2
B.264+1
C.264﹣1
D.232﹣1
【分析】把前面的1变为(2﹣1),再依次运用平方差公式进行计算即可.
【解答】解:原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1),
=(22﹣1)(22+1)(24+1)(28+1)(216+1)(232+1),
=(24﹣1)(24+1)(28+1)(216+1)(232+1),
=(28﹣1)(28+1)(216+1)(232+1),
=(216﹣1)(216+1)(232+1),
=(232﹣1)(232+1),
=264﹣1
故选:C.
二、多项选择题(每小题3分,共12分.每小题给出的4个选项中,有多选项是符合题目要求,全对的的3分,部分选对的的2分,有选错的的0分)
9.下面计算正确的是
AC .
A.(﹣0.2)0=1
B.(﹣0.1)﹣3=﹣
C.30÷3﹣1=3
D.a4÷a4=a(a≠0)
【分析】根据零指数幂对A选项进行判断;根据负整数指数幂的意义对B选项进行判断;利用零指数幂与负整数指数幂的意义对C进行判断;根据同底数幂的除法法则对D进行判断.
【解答】解:A.(﹣0.2)0=1,所以A选项符合题意;
B.(﹣0.1)﹣3==﹣1000,所以B选项不符合题意;
C.30÷3﹣1=1÷=1×3=3,所以C选项符合题意;
A.a4÷a4=a0=1(a≠0),所以D选项不符合题意.
故答案为AC.
10.在自习课上,小红为了检测同学们的学习效果,提出如下四种说法,其中错误的说法是
ABC .
A.三角形有且只有一条中线;
B.三角形的高一定在三角形内部;
C.三角形的两边之差大于第三边;
D.三角形按边分类可分为等腰三角形和不等边三角形.
【分析】根据三角形的分类、三角形的三边关系进行判断.
【解答】解:A.三角形有3条中线,原来的说法是错误的;
B.三角形的高不一定在三角形内部,原来的说法是错误的;
C.三角形的两边之差小于第三边,原来的说法是错误的;
D.三角形按边分类可分为等腰三角形和不等边三角形是正确的.
故答案为:ABC.
11.下列从左到右的变形,是因式分解的是
AD .
A.x2﹣9=(x+3)(x﹣3)
B.(y+1)(y﹣3)=(3﹣y)(y+1)
C.4yz﹣2y2z+z=2y(2z﹣zy)+z
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2
【分析】根据因式分解的定义,以及提公因式法和公式法进行判断求解.把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.
【解答】解:A.x2﹣9=(x+3)(x﹣3),把一个多项式化为几个整式的积的形式,是因式分解;
B.(y+1)(y﹣3)≠(3﹣y)(y+1);
C.4yz﹣2y2z+z=2y(2z﹣zy)+z,等式的右边不是几个整式的积的形式,不是因式分解;
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2,把一个多项式化为几个整式的积的形式,是因式分解;
故答案为:AD.
12.如图,其中能判断直线l1∥l2的条件有
ACD .
A.∠4=∠5
B.∠2+∠5=180°
C.∠1=∠3
D.∠6=∠1+∠2
【分析】平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;依此对各小题进行逐一判断即可.
【解答】解:①∵∠4=∠5,∴l1∥l2,故本条件符合题意;
②由∠2+∠5=180°不能得到l1∥l2,故本条件符合题意;
③∵∠1=∠3,∴l1∥l2,故本条件符合题意;
④∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件不合题意.
故答案为:ACD.
三、填空题(本题共8小题,共24分,只要求填写最后结果,每小题填对得3分)
13.若一个多边形的内角和为1080°,则这个多边形 8 边形.
【分析】首先设这个多边形的边数为n,由n边形的内角和等于180°(n﹣2),即可得方程180(n﹣2)=1080,解此方程即可求得答案.
【解答】解:设这个多边形的边数为n,
根据题意得:180(n﹣2)=1080,
解得:n=8,
故答案为:8.
14.(x+2)(2x﹣3)=2x2+mx﹣6,则m= 1 .
【分析】按照多项式乘以多项式把等式的左边展开,根据等式的左边等于右边,即可解答.
【解答】解:(x+2)(2x﹣3)=2x2﹣3x+4x﹣6=2x2+x﹣6=2x2+mx﹣6,
∴m=1,
故答案为:1.
15.学校位于小亮家北偏东35°方向,距离为300m,学校位于大刚家南偏东85°方向,距离也为300m,则大刚家相对与小亮家的位置是 北偏西25°方向,距离为300m .
【分析】由题意可知,小亮家、大刚家和学校构成了一个等边三角形,再根据“上北下南,左西右东“即可得出刚家相对与小亮家的位置.
【解答】解:据分析可知:小亮家、大刚家和学校构成了一个等边三角形,所以大刚家相对与小亮家的位置是北偏西25°方向,距离为300m.
故答案为北偏西25°方向,距离为300m.
16.计算= 2020 .
【分析】原式分母减数变形后,利用平方差公式计算即可求出值.
【解答】解:原式=
=
=
=2020.
故答案为:2020.
17.如果P(m+3,2m+4)在y轴上,那么点P的坐标是 (0,﹣2) .
【分析】点P在y轴上则该点横坐标为0,可解得m的值,从而得到点P的坐标.
【解答】解:∵P(m+3,2m+4)在y轴上,
∴m+3=0,得m=﹣3,
即2m+4=﹣2.即点P的坐标为(0,﹣2).
故答案为:(0,﹣2).
18.若关于x,y的二元一次方程组的解也是二元一次方程x﹣3y=6的解,则k= 1 .
【分析】把k看做已知数表示出方程组的解,代入已知方程求出k的值即可.
【解答】解:,
①+②得:2x=6k,即x=3k,
②﹣①得:2y=﹣2k,即y=﹣k,
把x=3k,y=﹣k代入x﹣3y=6中得:3k+3k=6,
解得:k=1,
故答案为:1
19.若多项式x2﹣(k+1)x+9是完全平方式,则k= 5或﹣7 .
【分析】利用完全平方公式的结构特征判断即可.
【解答】解:∵多项式x2﹣(k+1)x+9是完全平方式,
∴k+1=±6,
解得:k=5或﹣7,
故答案为:5或﹣7.
20.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式 a2﹣b2=(a+b)(a﹣b) .
【分析】左图中阴影部分的面积是a2﹣b2,右图中梯形的面积是(2a+2b)(a﹣b)=(a+b)(a﹣b),根据面积相等即可解答.
【解答】解:a2﹣b2=(a+b)(a﹣b).
四、解答题(本大题共7小题,共计60分)
21.(12分)计算:
(1)(2a)3﹣3a5÷a2;
(2)(x2y﹣2xy+y2)?(﹣4xy).
因式分解:
(3)x3﹣6x2+9x;
(4)a2(x﹣y)﹣9(x﹣y).
【分析】(1)利用积的乘方法则进行运算;
(2)利用单项式乘多项式法则进行运算;
(3)先提取公因式,再用完全平方公式进行分解;
(4)先提取公因式,再利用平方差公式因式分解.
【解答】解:(1)原式=8a3﹣3a3=5a3;
(2)原式=﹣2x3y2+8x2y2﹣4xy3;
(3)x3﹣6x2+9x
=x(x2﹣6x+9)
=x(x﹣3)2;
(4)a2(x﹣y)﹣9(x﹣y)
=(x﹣y)(a2﹣9)
=(x﹣y)(a+3)(a﹣3).
22.(8分)解下列方程组:
(1);
(2);
【分析】(1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
【解答】解:(1),
①×4+②×3得:25a=﹣25,
解得:a=﹣1,
把a=﹣1代入①得:b=0,
则方程组的解为;
(2)方程组整理得:,
①+②×3得:5x=﹣26,
解得:x=﹣5.2,
把x=﹣5.2代入②得:y=﹣4.8,
则方程组的解为.
23.(6分)如图,直线a∥b,直线AB与直线a,b分别相交于点A、B,AC交直线b于点C.
(1)若AC⊥AB,∠1=54°49′.求∠2的度数;
(2)请说明∠ABC+∠BCA+∠CAB=180°.
【分析】(1)依据直线a∥b,AC⊥AB,即可得到∠2=90°﹣∠3=35°11′;
(2)利用平行线的性质定理可得结论.
【解答】解:(1)如图,
∵直线a∥b,
∴∠3=∠1=54°49′,
又∵AC⊥AB,
∴∠2=90°﹣∠3=35°11′;
(2)∵a∥b,
∴∠ACB=∠3,
∠ABC=∠4,
∵∠4+∠3+∠BAC=180°,
∴∠ABC+∠BCA+∠CAB=180°.
24.(6分)观察下面的4个等式:
22﹣12=3,32﹣22=5,42﹣32=7,52﹣42=9.
(1)请你写出第5个等式 62﹣52=11 ;
(2)用含字母n的等式表示你发现的规律,并用学过的知识说明规律的正确性.
【分析】等式左边的底数为相邻的两个整数的平方差,右边是连续的奇数.
【解答】解:规律为:(n+1)2﹣n2=2n+1
因为,(n+1)2﹣n2=n2+2n+1﹣n2=2n+1
所以:(n+1)2﹣n2=2n+1
25.(8分)2020年疫情期间,山东省按“一省包一市”的方式,全力支援湖北省黄冈市,截止到2020年2月7日24时,共有确诊病例2044例,每六名轻症患者需要一名医护工作者.一名重症患者需要一名医护工作者,山东省共派去574名医护人员.请问轻症病人和重症病人各有多少名?
【分析】根据确诊病例数和医护人员数分别列方程,解方程即可求出轻症病人和重症病人各有多少名.
【解答】解:设轻症病人x人,重症病人y人,
根据题意得,
解得,
答:轻症病人有1764名,重症病人有280名.
26.(9分)△ABC的边AC在正方形网格中的位置如图所示,已知每个小正方形的边长为1,顶点A坐标为(﹣2,﹣2).
(1)请在网格图中建立并画出平面直角坐标系;
(2)直接写出点C的坐标为 (0,2) ;
(3)若点B的坐标为(3,﹣2),请在图中标出点B并画出△ABC;
(4)求△ABC的面积.
【分析】(1)根据点A的坐标建立平面直角坐标系;
(2)根据平面直角坐标系得到C的坐标;
(3)根据题意作出图形即可;
(4)根据A坐标为(﹣2,﹣2),C的坐标为(2,0),B的坐标为(3,﹣2),即可得到结论.
【解答】解:(1)如图所示;
(2)C的坐标为(0,2);
故答案为:(0,2);
(3)如图所示,△ABC即为所求;
(4)∵A坐标为(﹣2,﹣2),C的坐标为(2,0),B的坐标为(3,﹣2),∴S△ABC=×5×4=10.
27.(11分)如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
【分析】(1)先根据三角形内角和定理求出∠BAC的度数,再由角平分线的定义得出∠BAD的度数,再由AE⊥BC得出∠AEB=90°,进而可得出结论;
(2)同(1),可得∠ADE=75°,再由FE⊥BC可知∠FEB=90°,根据∠DFE=90°﹣∠ADE可得出结论.
【解答】解(1)∵∠B=40°,∠C=70°,
∴∠BAC=70°.
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°.
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°﹣∠ADE=15°;
(2)同(1),可得∠ADE=75°.
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°﹣∠ADE=15°.
同课章节目录
