山东省菏泽市单县2020-2021学年七年级下学期期末数学试卷(Word版 含答案)
文档属性
| 名称 | 山东省菏泽市单县2020-2021学年七年级下学期期末数学试卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 115.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 07:07:02 | ||
图片预览


文档简介
2020-2021学年山东省菏泽市单县七年级(下)期末数学试卷
一、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项A、B、C、D中,只有一个选项是正确的,请把正确的选项选出来并填涂在答题卡相应的位置上)
1.下列计算正确的是( )
A.x2+x2=2x4
B.x6÷x2=x3
C.x?x3=x4
D.(x2)3=x5
2.如图,有A,B,C三个地点,且AB⊥BC,B地在A地的北偏东43°方向,那么C地在B地的( )方向.
A.南偏东47°
B.南偏西43°
C.北偏东43°
D.北偏西47°
3.下列说法正确的是( )
A.过三角形的顶点,且过对边中点的直线是三角形的一条中线
B.六边形有九条对角线
C.直角三角形只有一条高
D.三角形任意两边之和不小于第三边
4.多项式2a2b3+8a4b2因式分解为( )
A.a2b2
(2b+8a2)
B.2ab2
(ab+4a3)
C.2a2b2
(b+4a2)
D.2a2b(b2+4a2b)
5.钟表上1时20分时,时针和分针的夹角是( )
A.80°
B.75°
C.70°
D.65°
6.若代数式M?(3x﹣y2)=y4﹣9x2,那么代数式M为( )
A.﹣3x﹣y2
B.﹣3x+y2
C.3x+y2
D.3x﹣y2
7.将一副直角三角板(∠A=30°,∠E=45°)按如图所示的位置摆放,使AB∥EF,则∠DOC的度数是( )
A.70°
B.75°
C.80°
D.85°
8.下列分解因式中正确的是( )
A.x2﹣4y=(x+2y)(x﹣2y)
B.﹣4x2﹣1=(﹣2x+1)(﹣2x﹣1)
C.x2+4x﹣4=(x﹣2)2
D.4x2﹣4x+1=(2x﹣1)2
9.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个
B.2个
C.1个
D.0个
10.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )
A.
B.
C.
D.
二、填空题(本大题共10个小题,每小题3分,共30分,只要求把结果填写在答题卡的相应区域内)
11.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是
.
12.若a=(﹣)﹣2,b=(﹣1)﹣1,c=(﹣)0,则a、b、c三个数中最大的数是
.
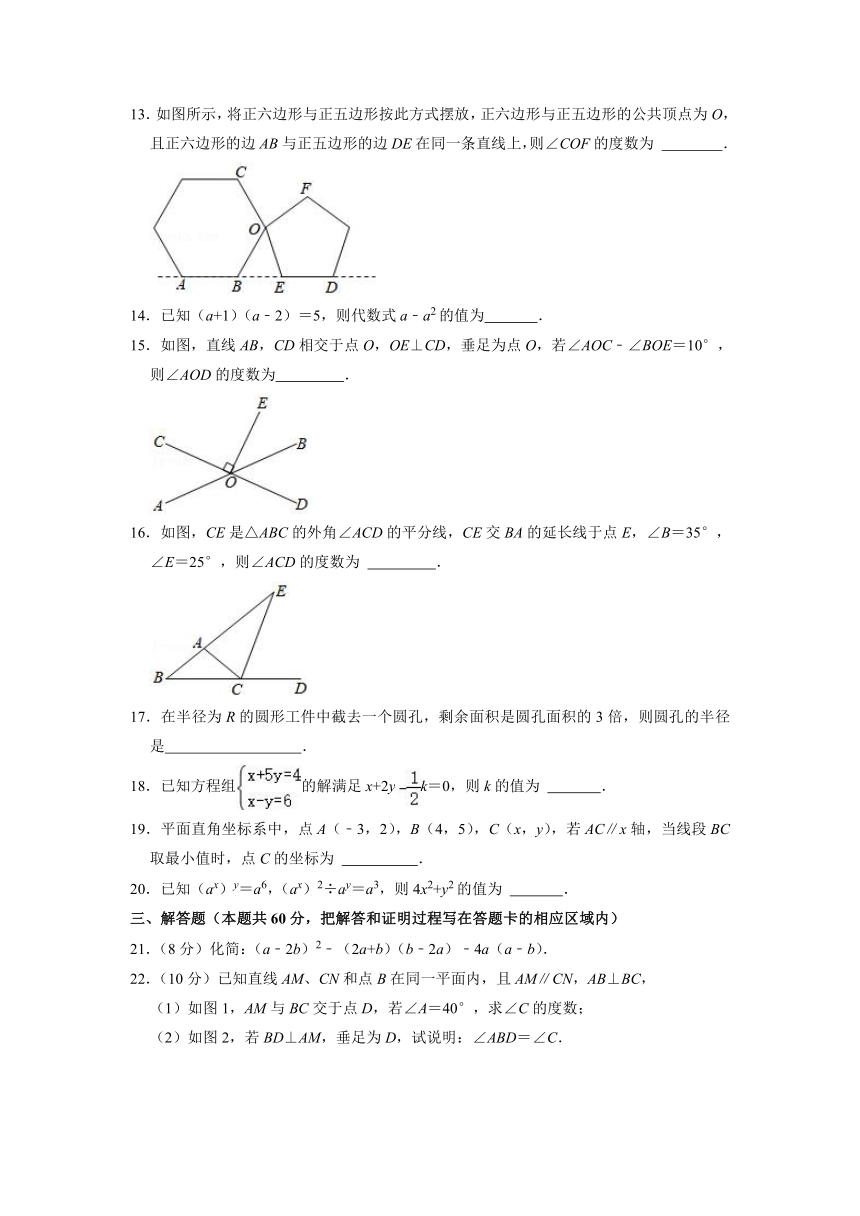
13.如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠COF的度数为
.
14.已知(a+1)(a﹣2)=5,则代数式a﹣a2的值为
.
15.如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O,若∠AOC﹣∠BOE=10°,则∠AOD的度数为
.
16.如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35°,∠E=25°,则∠ACD的度数为
.
17.在半径为R的圆形工件中截去一个圆孔,剩余面积是圆孔面积的3倍,则圆孔的半径是
.
18.已知方程组的解满足x+2yk=0,则k的值为
.
19.平面直角坐标系中,点A(﹣3,2),B(4,5),C(x,y),若AC∥x轴,当线段BC取最小值时,点C的坐标为
.
20.已知(ax)y=a6,(ax)2÷ay=a3,则4x2+y2的值为
.
三、解答题(本题共60分,把解答和证明过程写在答题卡的相应区域内)
21.(8分)化简:(a﹣2b)2﹣(2a+b)(b﹣2a)﹣4a(a﹣b).
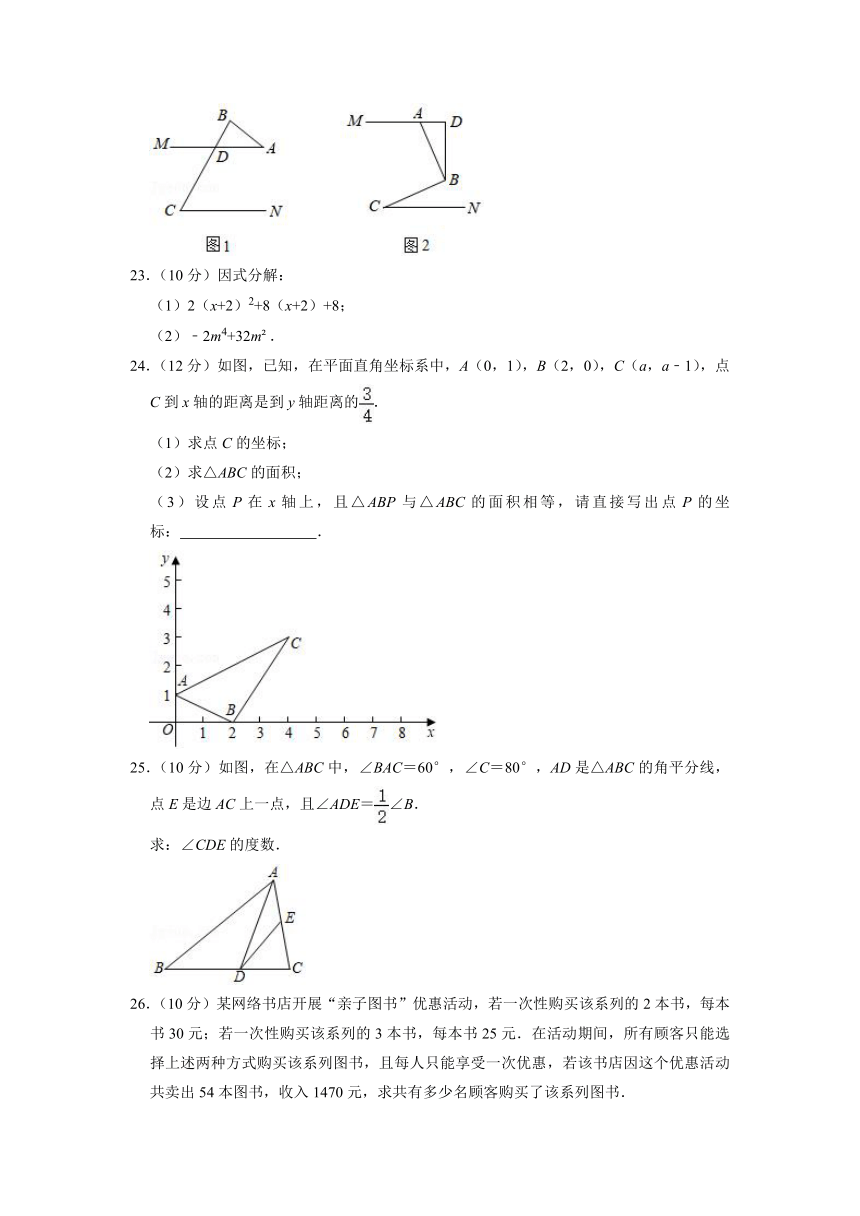
22.(10分)已知直线AM、CN和点B在同一平面内,且AM∥CN,AB⊥BC,
(1)如图1,AM与BC交于点D,若∠A=40°,求∠C的度数;
(2)如图2,若BD⊥AM,垂足为D,试说明:∠ABD=∠C.
23.(10分)因式分解:
(1)2(x+2)2+8(x+2)+8;
(2)﹣2m4+32m?.
24.(12分)如图,已知,在平面直角坐标系中,A(0,1),B(2,0),C(a,a﹣1),点C到x轴的距离是到y轴距离的.
(1)求点C的坐标;
(2)求△ABC的面积;
(3)设点P在x轴上,且△ABP与△ABC的面积相等,请直接写出点P的坐标:
.
25.(10分)如图,在△ABC中,∠BAC=60°,∠C=80°,AD是△ABC的角平分线,点E是边AC上一点,且∠ADE=∠B.
求:∠CDE的度数.
26.(10分)某网络书店开展“亲子图书”优惠活动,若一次性购买该系列的2本书,每本书30元;若一次性购买该系列的3本书,每本书25元.在活动期间,所有顾客只能选择上述两种方式购买该系列图书,且每人只能享受一次优惠,若该书店因这个优惠活动共卖出54本图书,收入1470元,求共有多少名顾客购买了该系列图书.
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项A、B、C、D中,只有一个选项是正确的,请把正确的选项选出来并填涂在答题卡相应的位置上)
1.
C.
2.
D.
3.B.
4.
C.
5.
A.
6.A.
7.
B.
8.
D.
9.A.
10.
B.
二、填空题(本大题共10个小题,每小题3分,共30分,只要求把结果填写在答题卡的相应区域内)
11.(﹣3,5).
12.
a.
13.
84°.
14.﹣7.
15.
130°.
16.
120°.
17..
18.
10.
19.(4,2).
20.
33.
三、解答题(本题共60分,把解答和证明过程写在答题卡的相应区域内)
21.
解:原式=a2﹣4ab+4b2﹣(b+2a)(b﹣2a)﹣4a2+4ab
=a2﹣4ab+4b2﹣b2+4a2﹣4a2+4ab
=a2+3b2.
22.
解:(1)∵∠A=40°,AB⊥BC,
∴∠ACB+∠A=90°,
∴∠ADB=90°﹣40°=50°,
∵AM∥CN,
∴∠C=∠ADB=50°,
两直线平行,内位角相等;
(2)延长DB交CN于点H,
∵MD∥CN,BD⊥AM,
∴BD⊥CN,
∴∠CHB=90°,
∵BD⊥AM,
∴∠DAB+∠ABD=90°,
∵AB⊥AM,
∴∠ABD+∠CBH=180°﹣∠ABC=180°﹣90°=90°,
∴∠DAB=∠CBH,
∵∠ABD=180°﹣∠D﹣∠BAD,
∠C=180°﹣∠CHB﹣∠CBH,
∴∠ABD=∠C.
23.
解:(1)2(x+2)2+8(x+2)+8
=2[(x+2)2+4(x+2)+4]
=2(x+2+2)2
=2(x+4)2;
(2)﹣2m4+32m2
=﹣2m2(m2﹣16)
=﹣2m2(m+4)(m﹣4).
24.
解:(1)∵点C到x轴的距离是到y轴距离的,C(a,a﹣1),
∴a﹣1=a,
∴a=4,
∴点C的坐标为:(4,3);
(2)过点C作CD⊥x轴于D,CE⊥y轴于E,如图所示:
则四边形DCEO为矩形,
∴S△ABC=S矩形DCEO﹣S△AEC﹣S△ABO﹣S△BCD=3×4﹣×2×4﹣×1×2﹣×2×3=12﹣4﹣1﹣3=4;
(3)设点P的坐标为(x,0),
则BP=|x﹣2|.
∵△ABP与△ABC的面积相等,
∴×1×|x﹣2|=4,
解得:x=10或x=﹣6,
∴点P的坐标为(10,0)或(﹣6,0),
故答案为:(10,0)或(﹣6,0).
25.
解:∵在△ABC中,∠BAC=60°,∠C=80°,
∴∠B=180°﹣60°﹣80°=40°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=30°,
∴∠ADC=∠B+∠BAD=70°,
∵∠ADE=∠B=20°,
∴∠CDE=∠ADC﹣∠ADE=70°﹣20°=50°.
26.
解:设用第一种方式购书的顾客有x人,用第二种方式购书的顾客有y人,由题意得:
.
解得.
∴x+y=22.
答:共有22名顾客购买了该系列图书.
一、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项A、B、C、D中,只有一个选项是正确的,请把正确的选项选出来并填涂在答题卡相应的位置上)
1.下列计算正确的是( )
A.x2+x2=2x4
B.x6÷x2=x3
C.x?x3=x4
D.(x2)3=x5
2.如图,有A,B,C三个地点,且AB⊥BC,B地在A地的北偏东43°方向,那么C地在B地的( )方向.
A.南偏东47°
B.南偏西43°
C.北偏东43°
D.北偏西47°
3.下列说法正确的是( )
A.过三角形的顶点,且过对边中点的直线是三角形的一条中线
B.六边形有九条对角线
C.直角三角形只有一条高
D.三角形任意两边之和不小于第三边
4.多项式2a2b3+8a4b2因式分解为( )
A.a2b2
(2b+8a2)
B.2ab2
(ab+4a3)
C.2a2b2
(b+4a2)
D.2a2b(b2+4a2b)
5.钟表上1时20分时,时针和分针的夹角是( )
A.80°
B.75°
C.70°
D.65°
6.若代数式M?(3x﹣y2)=y4﹣9x2,那么代数式M为( )
A.﹣3x﹣y2
B.﹣3x+y2
C.3x+y2
D.3x﹣y2
7.将一副直角三角板(∠A=30°,∠E=45°)按如图所示的位置摆放,使AB∥EF,则∠DOC的度数是( )
A.70°
B.75°
C.80°
D.85°
8.下列分解因式中正确的是( )
A.x2﹣4y=(x+2y)(x﹣2y)
B.﹣4x2﹣1=(﹣2x+1)(﹣2x﹣1)
C.x2+4x﹣4=(x﹣2)2
D.4x2﹣4x+1=(2x﹣1)2
9.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个
B.2个
C.1个
D.0个
10.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )
A.
B.
C.
D.
二、填空题(本大题共10个小题,每小题3分,共30分,只要求把结果填写在答题卡的相应区域内)
11.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是
.
12.若a=(﹣)﹣2,b=(﹣1)﹣1,c=(﹣)0,则a、b、c三个数中最大的数是
.
13.如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠COF的度数为
.
14.已知(a+1)(a﹣2)=5,则代数式a﹣a2的值为
.
15.如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O,若∠AOC﹣∠BOE=10°,则∠AOD的度数为
.
16.如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35°,∠E=25°,则∠ACD的度数为
.
17.在半径为R的圆形工件中截去一个圆孔,剩余面积是圆孔面积的3倍,则圆孔的半径是
.
18.已知方程组的解满足x+2yk=0,则k的值为
.
19.平面直角坐标系中,点A(﹣3,2),B(4,5),C(x,y),若AC∥x轴,当线段BC取最小值时,点C的坐标为
.
20.已知(ax)y=a6,(ax)2÷ay=a3,则4x2+y2的值为
.
三、解答题(本题共60分,把解答和证明过程写在答题卡的相应区域内)
21.(8分)化简:(a﹣2b)2﹣(2a+b)(b﹣2a)﹣4a(a﹣b).
22.(10分)已知直线AM、CN和点B在同一平面内,且AM∥CN,AB⊥BC,
(1)如图1,AM与BC交于点D,若∠A=40°,求∠C的度数;
(2)如图2,若BD⊥AM,垂足为D,试说明:∠ABD=∠C.
23.(10分)因式分解:
(1)2(x+2)2+8(x+2)+8;
(2)﹣2m4+32m?.
24.(12分)如图,已知,在平面直角坐标系中,A(0,1),B(2,0),C(a,a﹣1),点C到x轴的距离是到y轴距离的.
(1)求点C的坐标;
(2)求△ABC的面积;
(3)设点P在x轴上,且△ABP与△ABC的面积相等,请直接写出点P的坐标:
.
25.(10分)如图,在△ABC中,∠BAC=60°,∠C=80°,AD是△ABC的角平分线,点E是边AC上一点,且∠ADE=∠B.
求:∠CDE的度数.
26.(10分)某网络书店开展“亲子图书”优惠活动,若一次性购买该系列的2本书,每本书30元;若一次性购买该系列的3本书,每本书25元.在活动期间,所有顾客只能选择上述两种方式购买该系列图书,且每人只能享受一次优惠,若该书店因这个优惠活动共卖出54本图书,收入1470元,求共有多少名顾客购买了该系列图书.
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项A、B、C、D中,只有一个选项是正确的,请把正确的选项选出来并填涂在答题卡相应的位置上)
1.
C.
2.
D.
3.B.
4.
C.
5.
A.
6.A.
7.
B.
8.
D.
9.A.
10.
B.
二、填空题(本大题共10个小题,每小题3分,共30分,只要求把结果填写在答题卡的相应区域内)
11.(﹣3,5).
12.
a.
13.
84°.
14.﹣7.
15.
130°.
16.
120°.
17..
18.
10.
19.(4,2).
20.
33.
三、解答题(本题共60分,把解答和证明过程写在答题卡的相应区域内)
21.
解:原式=a2﹣4ab+4b2﹣(b+2a)(b﹣2a)﹣4a2+4ab
=a2﹣4ab+4b2﹣b2+4a2﹣4a2+4ab
=a2+3b2.
22.
解:(1)∵∠A=40°,AB⊥BC,
∴∠ACB+∠A=90°,
∴∠ADB=90°﹣40°=50°,
∵AM∥CN,
∴∠C=∠ADB=50°,
两直线平行,内位角相等;
(2)延长DB交CN于点H,
∵MD∥CN,BD⊥AM,
∴BD⊥CN,
∴∠CHB=90°,
∵BD⊥AM,
∴∠DAB+∠ABD=90°,
∵AB⊥AM,
∴∠ABD+∠CBH=180°﹣∠ABC=180°﹣90°=90°,
∴∠DAB=∠CBH,
∵∠ABD=180°﹣∠D﹣∠BAD,
∠C=180°﹣∠CHB﹣∠CBH,
∴∠ABD=∠C.
23.
解:(1)2(x+2)2+8(x+2)+8
=2[(x+2)2+4(x+2)+4]
=2(x+2+2)2
=2(x+4)2;
(2)﹣2m4+32m2
=﹣2m2(m2﹣16)
=﹣2m2(m+4)(m﹣4).
24.
解:(1)∵点C到x轴的距离是到y轴距离的,C(a,a﹣1),
∴a﹣1=a,
∴a=4,
∴点C的坐标为:(4,3);
(2)过点C作CD⊥x轴于D,CE⊥y轴于E,如图所示:
则四边形DCEO为矩形,
∴S△ABC=S矩形DCEO﹣S△AEC﹣S△ABO﹣S△BCD=3×4﹣×2×4﹣×1×2﹣×2×3=12﹣4﹣1﹣3=4;
(3)设点P的坐标为(x,0),
则BP=|x﹣2|.
∵△ABP与△ABC的面积相等,
∴×1×|x﹣2|=4,
解得:x=10或x=﹣6,
∴点P的坐标为(10,0)或(﹣6,0),
故答案为:(10,0)或(﹣6,0).
25.
解:∵在△ABC中,∠BAC=60°,∠C=80°,
∴∠B=180°﹣60°﹣80°=40°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=30°,
∴∠ADC=∠B+∠BAD=70°,
∵∠ADE=∠B=20°,
∴∠CDE=∠ADC﹣∠ADE=70°﹣20°=50°.
26.
解:设用第一种方式购书的顾客有x人,用第二种方式购书的顾客有y人,由题意得:
.
解得.
∴x+y=22.
答:共有22名顾客购买了该系列图书.
同课章节目录
