湖南省怀化市洪江一高2021-2022学年高一8月入学调研测评数学试题 (Word版,含解析)
文档属性
| 名称 | 湖南省怀化市洪江一高2021-2022学年高一8月入学调研测评数学试题 (Word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 757.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 13:23:26 | ||
图片预览



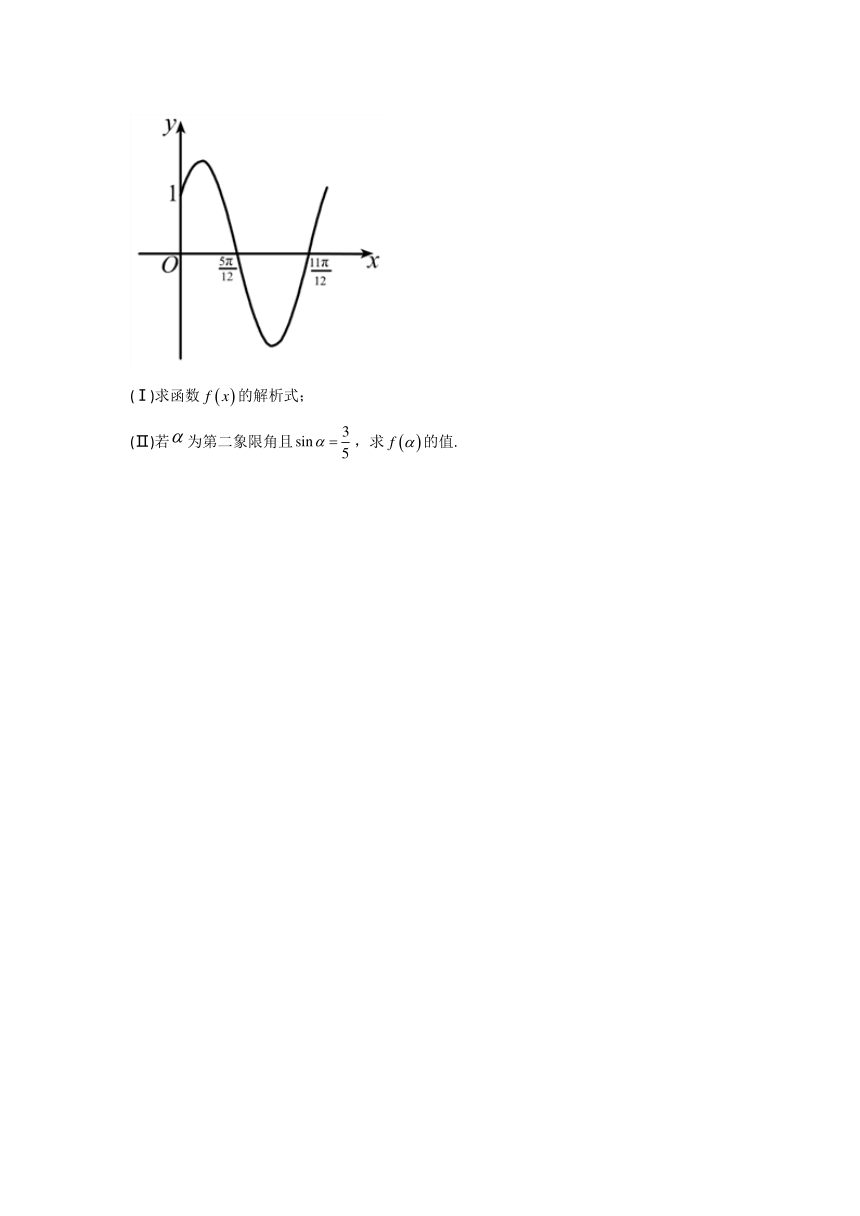

文档简介
洪江一高2021-2022学年高一8月入学调研测评
数学试卷
评卷人
得分
一、选择题
1.已知U为全集,则下列说法正确的是(
)
A.若,则
B.若,则或
C.若,则
D.若,则
2.设正数x,y,z满足,则当取得最大值时,的最大值是(
)
A.0
B.1
C.
D.3
3.函数在R上单调递减,且为奇函数.若,则满足的x的取值范围是(
)
A.
B.
C.
D.
4.将根式化简为指数式(
)
A.
B.
C.
D.
5.函数的值域为(
)
A.
B.
C.
D.
6.若过点可以作曲线的两条切线,则(
)
A.
B.
C.
D.
7.若,,则(
)
A.
B.
C.
D.
8.若(m,
),则(
)
A.
B.
C.
D.
评卷人
得分
二、填空题
9.计算:________;________.
10.函数的定义域为________,值域为________.
11.已知幂函数的图象过点,则__________.
评卷人
得分
三、多项选择题
12.若,,且,则下列不等式恒成立的是(
)
A.
B.
C.
D.
13.下列关于函数性质的描述,正确的是(
)
A.的定义域为
B.的值域为
C.在定义域上是增函数
D.的图象关于原点对称
14.对于函数定义域内的任意,当时,下述结论中正确的是(
)
A.
B.
C.
D.
15.对任意的正实数x,y,下列等式成立的是(
)
A.
B.
C.
D.
评卷人
得分
四、解答题
16.甲、乙两人解关于x的方程,甲写错了常数b,得到根,;乙写错了常数c,得到根,64.求原方程的根.
17.已知函数,(,且).
(1)求函数的定义域;
(2)判断函数的奇偶性,并予以证明.
18.某市出租车的收费标准是3千米以内(含3千米),收起步价8元;3千米至8千米(含8千米),超出3千米的部分按1.5元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
(1)计算某乘客搭乘出租车行驶7千米应付的车费;
(2)试写出车费y(元)与里程x(千米)之间的函数解析式并画出图像;
(3)小陈周末外出,行程为10千米,他设计了两种方案.
方案一:分两段乘车,乘一辆车行驶5千米,下车换乘另一辆车行驶5千米至目的地;
方案二:只乘一辆车至目的地.
试问:哪种方案更省钱?请说明理由.
19.某公司有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构进行培训.培训的总费用由两部分组成:一部分是给每位参加员工支付400元的培训材料费;另一部分是给培训机构缴纳的培训费.若参加培训的员工人数不超过30,则每人收取培训费1000元;若参加培训的员工人数超过30,则每超过1人,人均培训费减少20元.设公司参加培训的员工为x人,此次培训的总费用为y元.
(1)求出y与x之间的函数关系式;
(2)请你预算公司此次培训的总费用最多需要多少元.
20.已知函数(其中a,b为常数)的图象经过两点.
(1)判断并证明函数的奇偶性;
(2)证明函数在区间上单调递增.
21.已知函数的部分图象如图所示.
(Ⅰ)求函数的解析式;
(Ⅱ)若为第二象限角且,求的值.
参考答案
1.答案:ACD
解析:A说法正确,因为,,所以;B说法错误,若,则集合A,B不一定为空集,只需两个集合中无公共元素即可;C说法正确,因为,,所以;D说法正确,,即集合A,B中均无任何元素,可得.
2.答案:B
解析:由题意得,当且仅当时,等号成立,此时.故,当且仅当时,等号成立,故所求的最大值为1.
3.答案:D
解析:为奇函数,,
.又在R上单调递减,
,解得.故x的取值范围为.故选D.
4.答案:A
解析:
5.答案:A
解析:的定义域为,且在上是增函数,.故选A.
6.答案:D
解析:本题考查幂函数的图象与性质.因为曲线在R上单调递增,根据其图象可知要过点作曲线的两条切线,则点应在曲线与x轴之间,即.
7.答案:B
解析:,,.故选B.
8.答案:B
解析:,,即.故选B.
9.答案:8,1
解析:
10.答案:;
解析:由得,解得,函数的定义域为.
,,
,即,
函数的值域为.
11.答案:2
解析:设,,可得,,.
12.答案:AB
解析:因为,,且,
所以,即恒成立,故A正确;
由得,,所以,恒成立,故B正确,C错误;
由,,得,故D错误.故选AB.
13.答案:ABD
解析:由题意得,解得或,故函数的定义域为,故A正确.因为所以当时,;当时,,故的值域为,故B正确.由可得在定义域上不是增函数,故C不正确.当时,,且,故为上的奇函数,其图象关于原点对称,故D正确.
14.答案:CD
解析:对于A,函数的定义域为,故无意义,
A不正确;
对于B,当,时,,,B不正确;
对于C,,C正确·;
对于D,在上单调递增,则对任意的,,不妨设,都有,
,D正确.故选CD.
15.答案:ACD
解析:,中等式不成立.,,A,C,D中的等式显然成立.故选ACD.
16.答案:原方程可变形为.
甲写错了常数b,得到根,,
。
乙写错了常数c,得到根,64,
.
故原方程等价于,
即,
或,解得或.
故原方程的根为4,8.
解析:
17.答案:(1)要使函数有意义,
必须有解得.
所以函数的定义域是.
(2)函数是奇函数.证明如下:
由(1)知函数的定义域关于原点对称,
又
,
所以函数是奇函数.
解析:
18.答案:(1)由题意知,乘客搭乘出租车行驶7千米应付车费为(元).
(2)
(3)方案二更省钱.理由如下:
方案一的费用为(元).
方案二的费用为(元).
,
方案二更省钱.
解析:
19.答案:(1)当,时,;
当时,.
故
(2)当时,,所以当时,y取得最大值42000;
当时,,所以当时,y取得最大值50000.
综上所述,公司此次培训的总费用最多需要50000元.
解析:
20.答案:的图象经过两点,
解得.
(1)为奇函数.
证明:的定义域为,且为奇函数.
(2)证明:设,且,则.
.
,即,
在区间上单调递增.
解析:
21.答案:解:(1)由函数的部分图象知,
,解得;又函数图象过点,,
,,又,;
又函数图象过点,,解得,;
(2)为第二象限角且,,
,,
;
.
数学试卷
评卷人
得分
一、选择题
1.已知U为全集,则下列说法正确的是(
)
A.若,则
B.若,则或
C.若,则
D.若,则
2.设正数x,y,z满足,则当取得最大值时,的最大值是(
)
A.0
B.1
C.
D.3
3.函数在R上单调递减,且为奇函数.若,则满足的x的取值范围是(
)
A.
B.
C.
D.
4.将根式化简为指数式(
)
A.
B.
C.
D.
5.函数的值域为(
)
A.
B.
C.
D.
6.若过点可以作曲线的两条切线,则(
)
A.
B.
C.
D.
7.若,,则(
)
A.
B.
C.
D.
8.若(m,
),则(
)
A.
B.
C.
D.
评卷人
得分
二、填空题
9.计算:________;________.
10.函数的定义域为________,值域为________.
11.已知幂函数的图象过点,则__________.
评卷人
得分
三、多项选择题
12.若,,且,则下列不等式恒成立的是(
)
A.
B.
C.
D.
13.下列关于函数性质的描述,正确的是(
)
A.的定义域为
B.的值域为
C.在定义域上是增函数
D.的图象关于原点对称
14.对于函数定义域内的任意,当时,下述结论中正确的是(
)
A.
B.
C.
D.
15.对任意的正实数x,y,下列等式成立的是(
)
A.
B.
C.
D.
评卷人
得分
四、解答题
16.甲、乙两人解关于x的方程,甲写错了常数b,得到根,;乙写错了常数c,得到根,64.求原方程的根.
17.已知函数,(,且).
(1)求函数的定义域;
(2)判断函数的奇偶性,并予以证明.
18.某市出租车的收费标准是3千米以内(含3千米),收起步价8元;3千米至8千米(含8千米),超出3千米的部分按1.5元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
(1)计算某乘客搭乘出租车行驶7千米应付的车费;
(2)试写出车费y(元)与里程x(千米)之间的函数解析式并画出图像;
(3)小陈周末外出,行程为10千米,他设计了两种方案.
方案一:分两段乘车,乘一辆车行驶5千米,下车换乘另一辆车行驶5千米至目的地;
方案二:只乘一辆车至目的地.
试问:哪种方案更省钱?请说明理由.
19.某公司有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构进行培训.培训的总费用由两部分组成:一部分是给每位参加员工支付400元的培训材料费;另一部分是给培训机构缴纳的培训费.若参加培训的员工人数不超过30,则每人收取培训费1000元;若参加培训的员工人数超过30,则每超过1人,人均培训费减少20元.设公司参加培训的员工为x人,此次培训的总费用为y元.
(1)求出y与x之间的函数关系式;
(2)请你预算公司此次培训的总费用最多需要多少元.
20.已知函数(其中a,b为常数)的图象经过两点.
(1)判断并证明函数的奇偶性;
(2)证明函数在区间上单调递增.
21.已知函数的部分图象如图所示.
(Ⅰ)求函数的解析式;
(Ⅱ)若为第二象限角且,求的值.
参考答案
1.答案:ACD
解析:A说法正确,因为,,所以;B说法错误,若,则集合A,B不一定为空集,只需两个集合中无公共元素即可;C说法正确,因为,,所以;D说法正确,,即集合A,B中均无任何元素,可得.
2.答案:B
解析:由题意得,当且仅当时,等号成立,此时.故,当且仅当时,等号成立,故所求的最大值为1.
3.答案:D
解析:为奇函数,,
.又在R上单调递减,
,解得.故x的取值范围为.故选D.
4.答案:A
解析:
5.答案:A
解析:的定义域为,且在上是增函数,.故选A.
6.答案:D
解析:本题考查幂函数的图象与性质.因为曲线在R上单调递增,根据其图象可知要过点作曲线的两条切线,则点应在曲线与x轴之间,即.
7.答案:B
解析:,,.故选B.
8.答案:B
解析:,,即.故选B.
9.答案:8,1
解析:
10.答案:;
解析:由得,解得,函数的定义域为.
,,
,即,
函数的值域为.
11.答案:2
解析:设,,可得,,.
12.答案:AB
解析:因为,,且,
所以,即恒成立,故A正确;
由得,,所以,恒成立,故B正确,C错误;
由,,得,故D错误.故选AB.
13.答案:ABD
解析:由题意得,解得或,故函数的定义域为,故A正确.因为所以当时,;当时,,故的值域为,故B正确.由可得在定义域上不是增函数,故C不正确.当时,,且,故为上的奇函数,其图象关于原点对称,故D正确.
14.答案:CD
解析:对于A,函数的定义域为,故无意义,
A不正确;
对于B,当,时,,,B不正确;
对于C,,C正确·;
对于D,在上单调递增,则对任意的,,不妨设,都有,
,D正确.故选CD.
15.答案:ACD
解析:,中等式不成立.,,A,C,D中的等式显然成立.故选ACD.
16.答案:原方程可变形为.
甲写错了常数b,得到根,,
。
乙写错了常数c,得到根,64,
.
故原方程等价于,
即,
或,解得或.
故原方程的根为4,8.
解析:
17.答案:(1)要使函数有意义,
必须有解得.
所以函数的定义域是.
(2)函数是奇函数.证明如下:
由(1)知函数的定义域关于原点对称,
又
,
所以函数是奇函数.
解析:
18.答案:(1)由题意知,乘客搭乘出租车行驶7千米应付车费为(元).
(2)
(3)方案二更省钱.理由如下:
方案一的费用为(元).
方案二的费用为(元).
,
方案二更省钱.
解析:
19.答案:(1)当,时,;
当时,.
故
(2)当时,,所以当时,y取得最大值42000;
当时,,所以当时,y取得最大值50000.
综上所述,公司此次培训的总费用最多需要50000元.
解析:
20.答案:的图象经过两点,
解得.
(1)为奇函数.
证明:的定义域为,且为奇函数.
(2)证明:设,且,则.
.
,即,
在区间上单调递增.
解析:
21.答案:解:(1)由函数的部分图象知,
,解得;又函数图象过点,,
,,又,;
又函数图象过点,,解得,;
(2)为第二象限角且,,
,,
;
.
同课章节目录
