2021-2022学年华东师大新版七年级上册数学《第2章 有理数》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大新版七年级上册数学《第2章 有理数》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 174.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 07:25:46 | ||
图片预览



文档简介
2021-2022学年华东师大新版七年级上册数学《第2章
有理数》单元测试卷
一.选择题
1.中国人很早就开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入了负数.如果支出150元记作﹣150元,那么+80元表示( )
A.收入80元
B.支出80元
C.收入20元
D.支出20元
2.《九章算术》中注“今两算得失相反,要令正负以名之”,意思是:有两数若其意义相反,则分别叫做正数和负数.若气温为零上10℃记作+10℃,则﹣8℃表示气温为( )
A.零上8℃
B.零下8℃
C.零上2℃
D.零下2℃
3.冰箱冷藏室的温度为零上4℃,记作+4℃,则冷冻室的温度零下18℃,记作( )
A.18℃
B.﹣18℃
C.16℃
D.﹣16℃
4.如图,A,B,C,D是数轴上的四个点,其中最适合表示数π的点是( )
A.点A
B.点B
C.点C
D.点D
5.下列各数,﹣6,25,0,3.14,20%中,分数的个数是( )
A.1
B.2
C.3
D.4
6.下列各数中,与15互素的是( )
A.8
B.9
C.12
D.36
7.数轴上,到表示﹣3的点距离等于5个单位长度的点表示的数是( )
A.5或﹣5
B.2
C.﹣8
D.2或﹣8
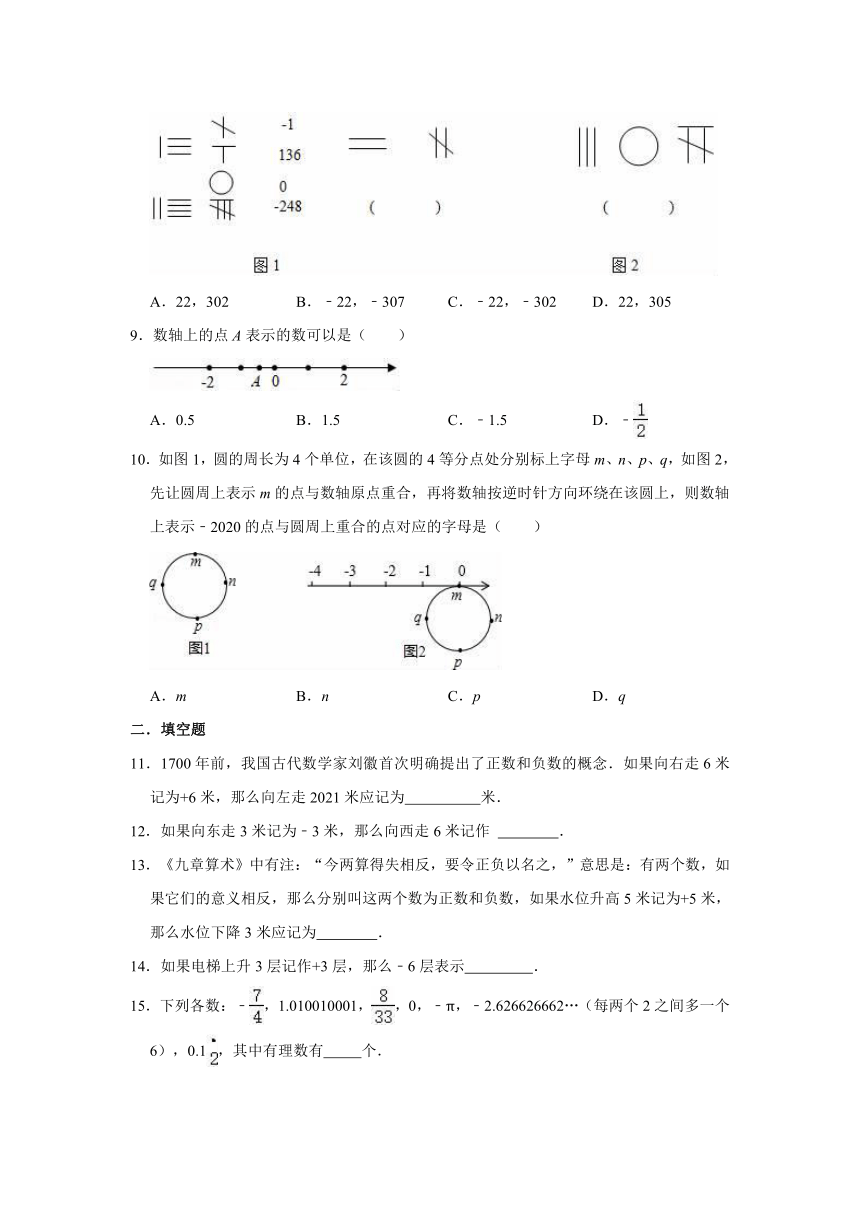
8.我国是较早认识负数的国家,南宋数学家李冶创造了在数字上划斜杠表示负数的方法(如图1所示).按照这样的规则,下面的两个数(图2)分别是( )
A.22,302
B.﹣22,﹣307
C.﹣22,﹣302
D.22,305
9.数轴上的点A表示的数可以是( )
A.0.5
B.1.5
C.﹣1.5
D.﹣
10.如图1,圆的周长为4个单位,在该圆的4等分点处分别标上字母m、n、p、q,如图2,先让圆周上表示m的点与数轴原点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示﹣2020的点与圆周上重合的点对应的字母是( )
A.m
B.n
C.p
D.q
二.填空题
11.1700年前,我国古代数学家刘徽首次明确提出了正数和负数的概念.如果向右走6米记为+6米,那么向左走2021米应记为
米.
12.如果向东走3米记为﹣3米,那么向西走6米记作
.
13.《九章算术》中有注:“今两算得失相反,要令正负以名之,”意思是:有两个数,如果它们的意义相反,那么分别叫这两个数为正数和负数,如果水位升高5米记为+5米,那么水位下降3米应记为
.
14.如果电梯上升3层记作+3层,那么﹣6层表示
.
15.下列各数:﹣,1.010010001,,0,﹣π,﹣2.626626662…(每两个2之间多一个6),0.1,其中有理数有
个.
16.在﹣2,6,0.9,0,中,非负整数有
.
17.数轴上点A表示0,那么到点A的距离是3个单位长度的点所表示的数是
.
18.在数轴上,P点对应的数为﹣4,把P点向左移动3个单位后再向右移1个单位长度,那么此时P点表示的数是
.
19.将数轴上表示数0的点记为点O,点A、点B分别从表示﹣4、12的点出发,同时向数轴负方向运动,速度分别为每秒2个单位长度和每秒6个单位长度,则经过
秒,OB=2OA.
20.如图:点A表示的数为
.
三.解答题
21.2017年国庆节期间,南宁动物园在7天假期中每天接待游客的人数与前一天相比的变化情况(正数表示比前一天多的人数,负数表示比前一天少的人数)如表:
日期
1日
2日
3日
4日
5日
6日
7日
人数变化/万人
+1.7
+0.6
+0.3
﹣0.3
﹣0.6
+0.2
﹣1.1
(1)请判断七天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(2)若9月30日的游客人数为3万人,求这7天的游客总人数是多少万人?
22.某大学图书馆上周借书记录(超过100册的部分记为正,少于100册的部分记为负)如下表:
星期一
星期二
星期三
星期四
星期五
星期六
﹣16
+28
+35
﹣14
0
﹣7
(1)该图书馆上星期五借出多少册书?
(2)该图书馆上个星期借书最多的一天比借书最少的一天多多少?
(3)该图书馆上星期借出多少册书?
23.一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭A出发,晚上停留在B处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):+5,﹣8,+10,﹣12,+6,﹣18,+5,﹣2.
(1)B处在岗亭A的什么方向?距离岗亭A多远?
(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
24.七年级一班第一学习小组共有8名同学.一次数学测验后,组长以90分为标准记录组员成绩,超过的分数记为正数,不足的分数记为负数,记录如下(单位:分):﹣7,﹣10,+9,+2,﹣1,+5,﹣8,+10.
(1)本次数学测验中第一组最高成绩为
分,最低成绩为
分;
(2)求第一小组此次数学测验的平均成绩.
25.随着我国经济的发展,股市得到迅速的发展,某支股票上个周五的收盘价为20元,下表是这支股票本周星期一至星期五的变化情况.(注:股市星期一至星期五开市,星期六、星期日休市)
星期
一
二
三
四
五
收盘价的变化(与前一天收盘价比较)
+1
﹣0.8
﹣0.6
0
+1.4
问(1)这支股票本周星期一的收盘价是
(2)这支股票本周星期三的收盘价是
(3)上周,股民李华以周五的收盘价20元/股买入这支股票1000股,本周,李华以周五的收盘价全部卖出这支股票1000股.按照国家规定,买(或卖)股票都要缴纳印花税、佣金等的股票交易费用,若规定,股票交易费用为买(或卖)股票的总成交金额的0.45%,那么,李华在这次买卖中,盈利还是亏损了多少?
26.定义:若有理数a,b满足等式a+b=ab+2,则称a,b是“雉水有理数对”,记作(a,b).如:数对(2,0),(,3)都是“雉水有理数对”.
(1)数对(4,)
(填“是”或“不是”)“雉水有理数对”;
(2)若(m,5)是“雉水有理数对”,求m的值;
(3)请写出一个符合条件的“锥水有理数对”
(注意:不能与题目中已有的“雉水有理数对”重复)
27.将下列各数填相应的集合圈内:20,﹣0.08,﹣2,4.5,3.14,﹣1,+,+5.
探索:这四个集合合并在一起是不是全体有理数集合?若不是,缺少的是哪一个数?
参考答案与试题解析
一.选择题
1.解:如果支出150元记作﹣150元,那么+80元表示收入80元.
故选:A.
2.解:若气温为零上10℃记作+10℃,则﹣8℃表示气温为零下8℃.
故选:B.
3.解:冰箱冷藏室的温度为零上4℃,记作+4℃,则冷冻室的温度零下18℃,记作﹣18℃
故选:B.
4.解:因为无理数π大于3,在数轴上表示大于3的点为点D;
故选:D.
5.解:由题意可知,分数有:,3.14,20%,共3个.
故选:C.
6.解:在8,9,12,36中,与15互素的数是8,
故选:A.
7.解:当点在表示﹣3的点的左边时,此时数为:﹣3+(﹣5)=﹣8,
当点在表示﹣3的点的右边时,此时数为:﹣3+(+5)=2,
所以数轴上,到表示﹣3的点距离等于5个单位长度的点表示的数是2或﹣8,
故选:D.
8.解:在算筹的个位数上用斜画一杠表示负数,“﹣22”写成:
“﹣307”写成:
故选:B.
9.解:由图可知,A点小于0,A点到原点的距离比A点到﹣2的距离小,
则A点可以是﹣,
故选:D.
10.解:由题意可得,
﹣1与q对应,﹣2与p对应,﹣3与n对应,﹣4与m对应,
﹣2020÷4=﹣505,
∴数轴上表示﹣2020的点与圆周上重合的点对应的字母是m,
故选:A.
二.填空题
11.解:如果向右走6米记为+6米,那么向左走2021米应记为﹣2021米,
故答案为:﹣2021.
12.解:根据题意,向西走6米记作﹣6米.
故答案为:﹣6米.
13.解:水位升高5米记为+5米,那么水位下降3米应记为﹣3米.
故答案为:﹣3米.
14.解:如果电梯上升3层记作+3层,那么﹣6层表示下降6层.
故答案为:下降6层.
15.解:有理数有﹣,1.010010001,,0,0.1,共5个;
﹣π,﹣2.626626662…(每两个2之间多一个6),是无理数;
故答案为:5.
16.解:在﹣2,6,0.9,0,中,非负整数有6,0,一共2个.
故答案为:6,0.
17.解:若该点在点A的左边,则0﹣3=﹣3,
若该点在点A的右边,则0+3=3.
故与点A的距离是3个单位长度的点表示的数是﹣3或3.
故答案为:﹣3或3.
18.解:根据题意,得
﹣4﹣3+1=﹣6,
则此时P点表示的数是﹣6;
故答案为:﹣6.
19.设点A,B运动的时间为ts,根据题意,得
ts后点A表示的数为﹣4﹣2t,点B表示的数为12﹣6t.
当OB=2OA时,需要以下几种情况讨论:
①当点B在原点的右侧时,12﹣6t=﹣2(﹣4﹣2t).解得t=0.4.符合题意;
②当点B在原点的左侧时,﹣(12﹣6t)=﹣2(﹣4﹣2t).解得t=10.符合题意.
综上知,经过0.4秒或10秒时,OB=2OA.
故答案为0.4或10.
20.解:根据勾股定理,得=,=,
∴点A表示的数为:﹣﹣1.
故答案为:﹣﹣1.
三.解答题
21.(10分)解:(1)10月1日至7日每天游客与9月30日相比的变化情况是:
1日:+1.7(万人)
2日:1.7+0.6=2.3(万人)
3日:2.3+0.3=2.6(万人)
4日:2.6﹣0.3=2.3(万人)
5日:2.3﹣0.6=1.7(万人)
6日:1.7+0.2=1.9(万人)
7日:1.9﹣1.1=0.8(万人)
所以游客人数最多的为3日,最少的为7日,这两天的游客人数相差2.6﹣0.8=1.8(万人)(5分)
(2)解法1:这七天的游客人数分别为:
1日:3+1.7=4.7(万人)
2日:4.7+0.6=5.3(万人)
3日:5.3+0.3=5.6(万人)
4日:5.6﹣0.3=5.3(万人)
5日:5.3﹣0.6=4.7(万人)
6日:4.7+0.2=4.9(万人)
7日:4.9﹣1.1=3.8(万人)
总人数:4.7+5.3+5.6+5.3+4.7+4.9+3.8=34.3(万人)
答:这7天的游客总人数是34.3万人(5分)
解法2:3×7+(1.7+2.3+.2.6+2.3+1.7+1.9+0.8)=21+13.3=34.3(万人)
答:这7天的游客总人数是34.3万人.
22.解:(1)根据题意得:100+0=100(册),
则星期五借出100册书;
(2)解法一:每天借出的册数分别为:84;128;135;86;100;93,
最多的比最少的多135﹣84=51(册);
解法二:35﹣(﹣16)=51(册)
该图书馆上个星期借书最多的一天比借书最少的一天多51册;
(3)根据题意得:84+128+135+86+100+93=626(册).
故该图书馆上星期共借出626册书.
23.解:(1)由题意得:
+5﹣8+10﹣12+6﹣18+5﹣2
=26﹣40
=﹣14
答:B处在岗亭A的西边,距离岗亭A有14km.
(2)设巡逻车总的行驶路程为S,则S=|+5|+|﹣8|+|+10|+|﹣12|+|+6|+|﹣18|+|+5|+|﹣2|
=5+8+10+12+6+18+5+2
=66
∵巡逻车每行驶1千米耗油0.1升,
∴耗油量为66×0.1=6.6
答:巡逻车这一天共耗油6.6升.
24.解:(1)90+10=100,90﹣10=80,
答:第一组最高成绩为100分,最低成绩为80分;
(2)(﹣7)+(﹣10)+9+2+(﹣1)+5+(﹣8)+10
=(﹣7﹣10﹣1﹣8)+(9+2+5+10)
=﹣26+26
=0,
90+×0=90(分).
答:第一小组此次数学测试的平均成绩为90分.
故答案为:100,80;
25.解:(1)20+1=21元.
故这支股票本周星期一的收盘价是21元;
故答案为:21元;
(2)20+1﹣0.8﹣0.6=19.6元.
故这支股票本周星期三的收盘价是19.6元;
故答案为:19.6元;
(3)20+1﹣0.8﹣0.6+0+1.4=21元,
21×1000×(1﹣0.45%)﹣20×1000×(1+0.45%),
=20905.5﹣20090,
=815.5元.
故李华在这次买卖中,盈利了815.5元.
26.解:(1)∵4+=,4×+2=,
∴4+=4×+2,
∴数对(4,)
是“雉水有理数对”;
故答案为:是;
(2)∵(m,5)是“雉水有理数对”,
∴m+5=5m+2,
m=,
(3)符合条件的“锥水有理数对”:(3,).
故答案为:(3,).
27.解:分类如下:
,
这四个集合合并在一起不是全体有理数集合,缺少的是0.
有理数》单元测试卷
一.选择题
1.中国人很早就开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入了负数.如果支出150元记作﹣150元,那么+80元表示( )
A.收入80元
B.支出80元
C.收入20元
D.支出20元
2.《九章算术》中注“今两算得失相反,要令正负以名之”,意思是:有两数若其意义相反,则分别叫做正数和负数.若气温为零上10℃记作+10℃,则﹣8℃表示气温为( )
A.零上8℃
B.零下8℃
C.零上2℃
D.零下2℃
3.冰箱冷藏室的温度为零上4℃,记作+4℃,则冷冻室的温度零下18℃,记作( )
A.18℃
B.﹣18℃
C.16℃
D.﹣16℃
4.如图,A,B,C,D是数轴上的四个点,其中最适合表示数π的点是( )
A.点A
B.点B
C.点C
D.点D
5.下列各数,﹣6,25,0,3.14,20%中,分数的个数是( )
A.1
B.2
C.3
D.4
6.下列各数中,与15互素的是( )
A.8
B.9
C.12
D.36
7.数轴上,到表示﹣3的点距离等于5个单位长度的点表示的数是( )
A.5或﹣5
B.2
C.﹣8
D.2或﹣8
8.我国是较早认识负数的国家,南宋数学家李冶创造了在数字上划斜杠表示负数的方法(如图1所示).按照这样的规则,下面的两个数(图2)分别是( )
A.22,302
B.﹣22,﹣307
C.﹣22,﹣302
D.22,305
9.数轴上的点A表示的数可以是( )
A.0.5
B.1.5
C.﹣1.5
D.﹣
10.如图1,圆的周长为4个单位,在该圆的4等分点处分别标上字母m、n、p、q,如图2,先让圆周上表示m的点与数轴原点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示﹣2020的点与圆周上重合的点对应的字母是( )
A.m
B.n
C.p
D.q
二.填空题
11.1700年前,我国古代数学家刘徽首次明确提出了正数和负数的概念.如果向右走6米记为+6米,那么向左走2021米应记为
米.
12.如果向东走3米记为﹣3米,那么向西走6米记作
.
13.《九章算术》中有注:“今两算得失相反,要令正负以名之,”意思是:有两个数,如果它们的意义相反,那么分别叫这两个数为正数和负数,如果水位升高5米记为+5米,那么水位下降3米应记为
.
14.如果电梯上升3层记作+3层,那么﹣6层表示
.
15.下列各数:﹣,1.010010001,,0,﹣π,﹣2.626626662…(每两个2之间多一个6),0.1,其中有理数有
个.
16.在﹣2,6,0.9,0,中,非负整数有
.
17.数轴上点A表示0,那么到点A的距离是3个单位长度的点所表示的数是
.
18.在数轴上,P点对应的数为﹣4,把P点向左移动3个单位后再向右移1个单位长度,那么此时P点表示的数是
.
19.将数轴上表示数0的点记为点O,点A、点B分别从表示﹣4、12的点出发,同时向数轴负方向运动,速度分别为每秒2个单位长度和每秒6个单位长度,则经过
秒,OB=2OA.
20.如图:点A表示的数为
.
三.解答题
21.2017年国庆节期间,南宁动物园在7天假期中每天接待游客的人数与前一天相比的变化情况(正数表示比前一天多的人数,负数表示比前一天少的人数)如表:
日期
1日
2日
3日
4日
5日
6日
7日
人数变化/万人
+1.7
+0.6
+0.3
﹣0.3
﹣0.6
+0.2
﹣1.1
(1)请判断七天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(2)若9月30日的游客人数为3万人,求这7天的游客总人数是多少万人?
22.某大学图书馆上周借书记录(超过100册的部分记为正,少于100册的部分记为负)如下表:
星期一
星期二
星期三
星期四
星期五
星期六
﹣16
+28
+35
﹣14
0
﹣7
(1)该图书馆上星期五借出多少册书?
(2)该图书馆上个星期借书最多的一天比借书最少的一天多多少?
(3)该图书馆上星期借出多少册书?
23.一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭A出发,晚上停留在B处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):+5,﹣8,+10,﹣12,+6,﹣18,+5,﹣2.
(1)B处在岗亭A的什么方向?距离岗亭A多远?
(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
24.七年级一班第一学习小组共有8名同学.一次数学测验后,组长以90分为标准记录组员成绩,超过的分数记为正数,不足的分数记为负数,记录如下(单位:分):﹣7,﹣10,+9,+2,﹣1,+5,﹣8,+10.
(1)本次数学测验中第一组最高成绩为
分,最低成绩为
分;
(2)求第一小组此次数学测验的平均成绩.
25.随着我国经济的发展,股市得到迅速的发展,某支股票上个周五的收盘价为20元,下表是这支股票本周星期一至星期五的变化情况.(注:股市星期一至星期五开市,星期六、星期日休市)
星期
一
二
三
四
五
收盘价的变化(与前一天收盘价比较)
+1
﹣0.8
﹣0.6
0
+1.4
问(1)这支股票本周星期一的收盘价是
(2)这支股票本周星期三的收盘价是
(3)上周,股民李华以周五的收盘价20元/股买入这支股票1000股,本周,李华以周五的收盘价全部卖出这支股票1000股.按照国家规定,买(或卖)股票都要缴纳印花税、佣金等的股票交易费用,若规定,股票交易费用为买(或卖)股票的总成交金额的0.45%,那么,李华在这次买卖中,盈利还是亏损了多少?
26.定义:若有理数a,b满足等式a+b=ab+2,则称a,b是“雉水有理数对”,记作(a,b).如:数对(2,0),(,3)都是“雉水有理数对”.
(1)数对(4,)
(填“是”或“不是”)“雉水有理数对”;
(2)若(m,5)是“雉水有理数对”,求m的值;
(3)请写出一个符合条件的“锥水有理数对”
(注意:不能与题目中已有的“雉水有理数对”重复)
27.将下列各数填相应的集合圈内:20,﹣0.08,﹣2,4.5,3.14,﹣1,+,+5.
探索:这四个集合合并在一起是不是全体有理数集合?若不是,缺少的是哪一个数?
参考答案与试题解析
一.选择题
1.解:如果支出150元记作﹣150元,那么+80元表示收入80元.
故选:A.
2.解:若气温为零上10℃记作+10℃,则﹣8℃表示气温为零下8℃.
故选:B.
3.解:冰箱冷藏室的温度为零上4℃,记作+4℃,则冷冻室的温度零下18℃,记作﹣18℃
故选:B.
4.解:因为无理数π大于3,在数轴上表示大于3的点为点D;
故选:D.
5.解:由题意可知,分数有:,3.14,20%,共3个.
故选:C.
6.解:在8,9,12,36中,与15互素的数是8,
故选:A.
7.解:当点在表示﹣3的点的左边时,此时数为:﹣3+(﹣5)=﹣8,
当点在表示﹣3的点的右边时,此时数为:﹣3+(+5)=2,
所以数轴上,到表示﹣3的点距离等于5个单位长度的点表示的数是2或﹣8,
故选:D.
8.解:在算筹的个位数上用斜画一杠表示负数,“﹣22”写成:
“﹣307”写成:
故选:B.
9.解:由图可知,A点小于0,A点到原点的距离比A点到﹣2的距离小,
则A点可以是﹣,
故选:D.
10.解:由题意可得,
﹣1与q对应,﹣2与p对应,﹣3与n对应,﹣4与m对应,
﹣2020÷4=﹣505,
∴数轴上表示﹣2020的点与圆周上重合的点对应的字母是m,
故选:A.
二.填空题
11.解:如果向右走6米记为+6米,那么向左走2021米应记为﹣2021米,
故答案为:﹣2021.
12.解:根据题意,向西走6米记作﹣6米.
故答案为:﹣6米.
13.解:水位升高5米记为+5米,那么水位下降3米应记为﹣3米.
故答案为:﹣3米.
14.解:如果电梯上升3层记作+3层,那么﹣6层表示下降6层.
故答案为:下降6层.
15.解:有理数有﹣,1.010010001,,0,0.1,共5个;
﹣π,﹣2.626626662…(每两个2之间多一个6),是无理数;
故答案为:5.
16.解:在﹣2,6,0.9,0,中,非负整数有6,0,一共2个.
故答案为:6,0.
17.解:若该点在点A的左边,则0﹣3=﹣3,
若该点在点A的右边,则0+3=3.
故与点A的距离是3个单位长度的点表示的数是﹣3或3.
故答案为:﹣3或3.
18.解:根据题意,得
﹣4﹣3+1=﹣6,
则此时P点表示的数是﹣6;
故答案为:﹣6.
19.设点A,B运动的时间为ts,根据题意,得
ts后点A表示的数为﹣4﹣2t,点B表示的数为12﹣6t.
当OB=2OA时,需要以下几种情况讨论:
①当点B在原点的右侧时,12﹣6t=﹣2(﹣4﹣2t).解得t=0.4.符合题意;
②当点B在原点的左侧时,﹣(12﹣6t)=﹣2(﹣4﹣2t).解得t=10.符合题意.
综上知,经过0.4秒或10秒时,OB=2OA.
故答案为0.4或10.
20.解:根据勾股定理,得=,=,
∴点A表示的数为:﹣﹣1.
故答案为:﹣﹣1.
三.解答题
21.(10分)解:(1)10月1日至7日每天游客与9月30日相比的变化情况是:
1日:+1.7(万人)
2日:1.7+0.6=2.3(万人)
3日:2.3+0.3=2.6(万人)
4日:2.6﹣0.3=2.3(万人)
5日:2.3﹣0.6=1.7(万人)
6日:1.7+0.2=1.9(万人)
7日:1.9﹣1.1=0.8(万人)
所以游客人数最多的为3日,最少的为7日,这两天的游客人数相差2.6﹣0.8=1.8(万人)(5分)
(2)解法1:这七天的游客人数分别为:
1日:3+1.7=4.7(万人)
2日:4.7+0.6=5.3(万人)
3日:5.3+0.3=5.6(万人)
4日:5.6﹣0.3=5.3(万人)
5日:5.3﹣0.6=4.7(万人)
6日:4.7+0.2=4.9(万人)
7日:4.9﹣1.1=3.8(万人)
总人数:4.7+5.3+5.6+5.3+4.7+4.9+3.8=34.3(万人)
答:这7天的游客总人数是34.3万人(5分)
解法2:3×7+(1.7+2.3+.2.6+2.3+1.7+1.9+0.8)=21+13.3=34.3(万人)
答:这7天的游客总人数是34.3万人.
22.解:(1)根据题意得:100+0=100(册),
则星期五借出100册书;
(2)解法一:每天借出的册数分别为:84;128;135;86;100;93,
最多的比最少的多135﹣84=51(册);
解法二:35﹣(﹣16)=51(册)
该图书馆上个星期借书最多的一天比借书最少的一天多51册;
(3)根据题意得:84+128+135+86+100+93=626(册).
故该图书馆上星期共借出626册书.
23.解:(1)由题意得:
+5﹣8+10﹣12+6﹣18+5﹣2
=26﹣40
=﹣14
答:B处在岗亭A的西边,距离岗亭A有14km.
(2)设巡逻车总的行驶路程为S,则S=|+5|+|﹣8|+|+10|+|﹣12|+|+6|+|﹣18|+|+5|+|﹣2|
=5+8+10+12+6+18+5+2
=66
∵巡逻车每行驶1千米耗油0.1升,
∴耗油量为66×0.1=6.6
答:巡逻车这一天共耗油6.6升.
24.解:(1)90+10=100,90﹣10=80,
答:第一组最高成绩为100分,最低成绩为80分;
(2)(﹣7)+(﹣10)+9+2+(﹣1)+5+(﹣8)+10
=(﹣7﹣10﹣1﹣8)+(9+2+5+10)
=﹣26+26
=0,
90+×0=90(分).
答:第一小组此次数学测试的平均成绩为90分.
故答案为:100,80;
25.解:(1)20+1=21元.
故这支股票本周星期一的收盘价是21元;
故答案为:21元;
(2)20+1﹣0.8﹣0.6=19.6元.
故这支股票本周星期三的收盘价是19.6元;
故答案为:19.6元;
(3)20+1﹣0.8﹣0.6+0+1.4=21元,
21×1000×(1﹣0.45%)﹣20×1000×(1+0.45%),
=20905.5﹣20090,
=815.5元.
故李华在这次买卖中,盈利了815.5元.
26.解:(1)∵4+=,4×+2=,
∴4+=4×+2,
∴数对(4,)
是“雉水有理数对”;
故答案为:是;
(2)∵(m,5)是“雉水有理数对”,
∴m+5=5m+2,
m=,
(3)符合条件的“锥水有理数对”:(3,).
故答案为:(3,).
27.解:分类如下:
,
这四个集合合并在一起不是全体有理数集合,缺少的是0.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
