华师大版数学九年级上册 第22章一元二次方程复习课件(16张PPT)
文档属性
| 名称 | 华师大版数学九年级上册 第22章一元二次方程复习课件(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 624.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 09:56:03 | ||
图片预览






文档简介
(共16张PPT)
复习课:
第22章
一元二次方程
1.
了解一元二次方程的有关概念,掌握一元二次方程的一般形式;
2.
掌握一元二次方程的解法;
3.
掌握一元二次方程根的判别式,了解一元二次方程根与系数的关系;
4.
会建立一元二次方程模型解决实际问题。
复习目标:
一、一元二次方程的定义及一般形式:
1.
判定一元二次方程的三个条件:
①只有一个未知数;
②未知数的最高次数是2;
③方程两边都是整式。
2.一元二次方程的一般形式是
练一练:
1.下列方程,是一元二次方程的是(
)
A.
B.
C.
D.
C
2.
当m
时,方程mx2-3x=2x2-mx+2
是一元二次方程.
当m
时,方程(m2-4)x2-(m+2)x-3=0是一元一次方程.
≠2
=2
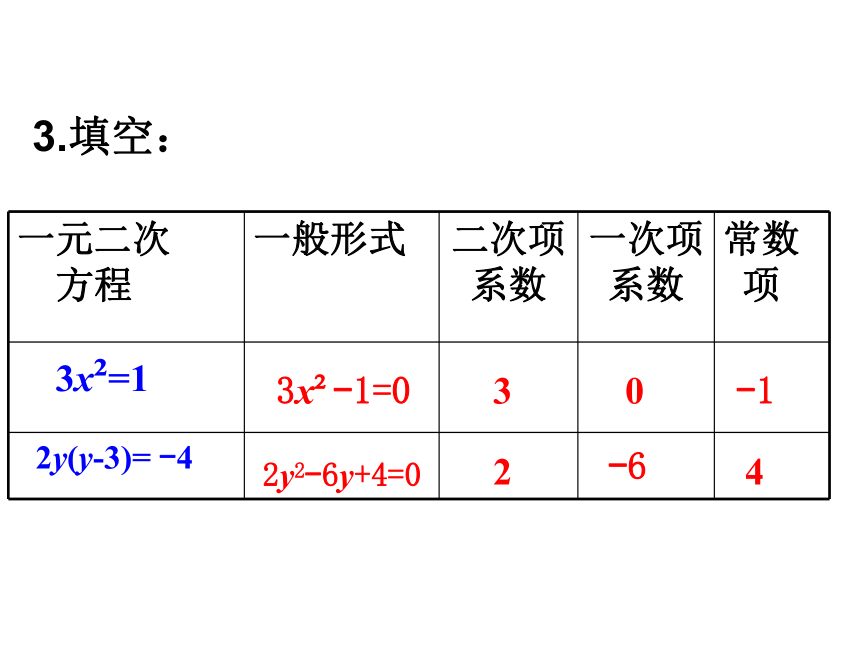
一元二次
方程
一般形式
二次项系数
一次项系数
常数
项
3x?=1
2y(y-3)=
-4
3x?-1=0
3
2
-6
-1
4
0
2y2-6y+4=0
3.填空:
二、一元二次方程的解法
1.直接开平方法:
2.因式分解法:
3.配方法:
4.公式法:
(ax+b)2=n
(a≠0,n≥0)
1.提取公因式法
2.平方差公式
3.十字相乘法
当b-4ac≥0时,x=
当二次项系数为1的时候,
方程两边同时加上一次项
系数一半的平方
用适当的方法解下列方程:
练习:
(1)x2-3x=0
(2)(2x-1)2=9
(3)x2-4x=1
(4)x2-3x+1=0
x1=0,x2=3
x1=2,x2=-1
三、一元二次方程ax2+bx+c=0(a≠0)根的
判别式:
?=b2-4ac
当?
>0
当?
=0
当?
<0
方程有两个不相等的实数根
方程有两个相等的实数根
方程没有实数根
练习:
方程x2-4x+4=0根的情况是(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
B
例1:
书P30例3:已知关于x的方程
(m-2)x2-2(m-1)x+m+1=0,当m为何非负整数时,
(1)方程只有一个实数根?
(2)方程有两个相等的实数根?
(3)方程有两个不相等的实数根?
四、一元二次方程根与系数的关系
方程ax2+bx+c=0(a≠0)的两根为x1,x2
,则有x1+x2=
,x1.x2=
练习:
1.
已知方程
的一个根为2,
则k=
,另一个根为
。
-7
2.设一元二次方程
的两个根
为x1,x2,则
=________
;
=
________;
=__________,
x12-3x2+5=_________.
11
3
-11
15
例2:P31例4.已知关于x的一元二次方程x2-2x+a=0的两个实数根x1,x2
满足x1x2+x1+x2>0,求a的取值范围。
(1)
审
(2)
设
(3)
列
(4)
解
(5)
验
(6)
答
五、列一元二次方程解应用题的一般步骤:
例3:P31例5.某公司今年1月份的生产成本中是400万元,由于改进生产技术,生产成本逐月下降,3月份的生产成本是361万元。假设该公司2、3、4月每个月生产成本的下降率都相同。
(1)求每个月生产成本的下降率;
(2)请你预测4月份该公司的生产成本。
(1)400(1-x)2=361
例4:某商场销售一批名牌衬衫,平均每天可售出20件,每件售价60元,每件成本20元,为了扩大销售量,增加盈利,减少库存,商场决定采取适当的降价措施,经调查发现每降价1元,商场每天可以多售2件。若每天实现盈利1200元,衬衫应降价多少元?
(20+2x)(60-20-x)=1200
x1=10,x2=20
经检验x1=10不合题意,舍去
作业:
1.记忆相关知识点;
2.完成点击中考上相应练习。
复习课:
第22章
一元二次方程
1.
了解一元二次方程的有关概念,掌握一元二次方程的一般形式;
2.
掌握一元二次方程的解法;
3.
掌握一元二次方程根的判别式,了解一元二次方程根与系数的关系;
4.
会建立一元二次方程模型解决实际问题。
复习目标:
一、一元二次方程的定义及一般形式:
1.
判定一元二次方程的三个条件:
①只有一个未知数;
②未知数的最高次数是2;
③方程两边都是整式。
2.一元二次方程的一般形式是
练一练:
1.下列方程,是一元二次方程的是(
)
A.
B.
C.
D.
C
2.
当m
时,方程mx2-3x=2x2-mx+2
是一元二次方程.
当m
时,方程(m2-4)x2-(m+2)x-3=0是一元一次方程.
≠2
=2
一元二次
方程
一般形式
二次项系数
一次项系数
常数
项
3x?=1
2y(y-3)=
-4
3x?-1=0
3
2
-6
-1
4
0
2y2-6y+4=0
3.填空:
二、一元二次方程的解法
1.直接开平方法:
2.因式分解法:
3.配方法:
4.公式法:
(ax+b)2=n
(a≠0,n≥0)
1.提取公因式法
2.平方差公式
3.十字相乘法
当b-4ac≥0时,x=
当二次项系数为1的时候,
方程两边同时加上一次项
系数一半的平方
用适当的方法解下列方程:
练习:
(1)x2-3x=0
(2)(2x-1)2=9
(3)x2-4x=1
(4)x2-3x+1=0
x1=0,x2=3
x1=2,x2=-1
三、一元二次方程ax2+bx+c=0(a≠0)根的
判别式:
?=b2-4ac
当?
>0
当?
=0
当?
<0
方程有两个不相等的实数根
方程有两个相等的实数根
方程没有实数根
练习:
方程x2-4x+4=0根的情况是(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
B
例1:
书P30例3:已知关于x的方程
(m-2)x2-2(m-1)x+m+1=0,当m为何非负整数时,
(1)方程只有一个实数根?
(2)方程有两个相等的实数根?
(3)方程有两个不相等的实数根?
四、一元二次方程根与系数的关系
方程ax2+bx+c=0(a≠0)的两根为x1,x2
,则有x1+x2=
,x1.x2=
练习:
1.
已知方程
的一个根为2,
则k=
,另一个根为
。
-7
2.设一元二次方程
的两个根
为x1,x2,则
=________
;
=
________;
=__________,
x12-3x2+5=_________.
11
3
-11
15
例2:P31例4.已知关于x的一元二次方程x2-2x+a=0的两个实数根x1,x2
满足x1x2+x1+x2>0,求a的取值范围。
(1)
审
(2)
设
(3)
列
(4)
解
(5)
验
(6)
答
五、列一元二次方程解应用题的一般步骤:
例3:P31例5.某公司今年1月份的生产成本中是400万元,由于改进生产技术,生产成本逐月下降,3月份的生产成本是361万元。假设该公司2、3、4月每个月生产成本的下降率都相同。
(1)求每个月生产成本的下降率;
(2)请你预测4月份该公司的生产成本。
(1)400(1-x)2=361
例4:某商场销售一批名牌衬衫,平均每天可售出20件,每件售价60元,每件成本20元,为了扩大销售量,增加盈利,减少库存,商场决定采取适当的降价措施,经调查发现每降价1元,商场每天可以多售2件。若每天实现盈利1200元,衬衫应降价多少元?
(20+2x)(60-20-x)=1200
x1=10,x2=20
经检验x1=10不合题意,舍去
作业:
1.记忆相关知识点;
2.完成点击中考上相应练习。
