11.3.2多边形的内角和与外角和 课件(共21张PPT)
文档属性
| 名称 | 11.3.2多边形的内角和与外角和 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 15:02:47 | ||
图片预览







文档简介
(共23张PPT)
人教版
八年级上
多边形的内角和与外角和
1.了解并掌握多边形内角和与外角和公式.
2.理解多边形内角和与外角和公式的推导过程(重点)
3.灵活运用多边形的内角和与外角和定理解决实际问题.(难点)
学习目标
问题1:你能说出三角形的内角和是多少度吗?
三角形的内角和是180°
问题2:你知道长方形和正方形的内角和是多少度吗?
长方形和正方形的内角和都是360°
问题3:你能猜测任意一个四边形的内角和是多少度吗?
任意一个四边形的内角是360°
复习导入
请大家任意画一个四边形,用量角器量出四个内角的大小,并计算出四个内角的和是多少?
经过测量发现四边形的四个内角和为360°.
复习导入
A
B
D
C
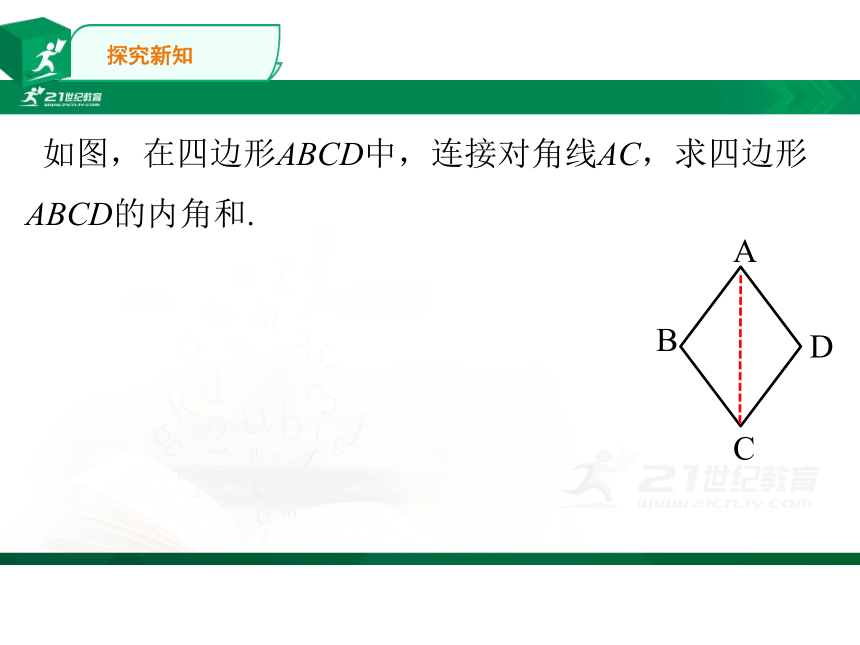
如图,在四边形ABCD中,连接对角线AC,求四边形ABCD的内角和.
探究新知
解:∵对角线AC将四边形分为△ACD和△ACB,
∴在△ACD中,∠D+∠DAC+∠DCA=180°,
在△ACB中,∠B+∠BAC+∠BCA=180°.
∵∠D+∠DAC+∠DCA+∠B+∠BAC+∠BCA=360°,
∴∠D+∠DAB+∠B+∠BCD=360°.
∴四边形ABCD的内角和为360°..
探究新知
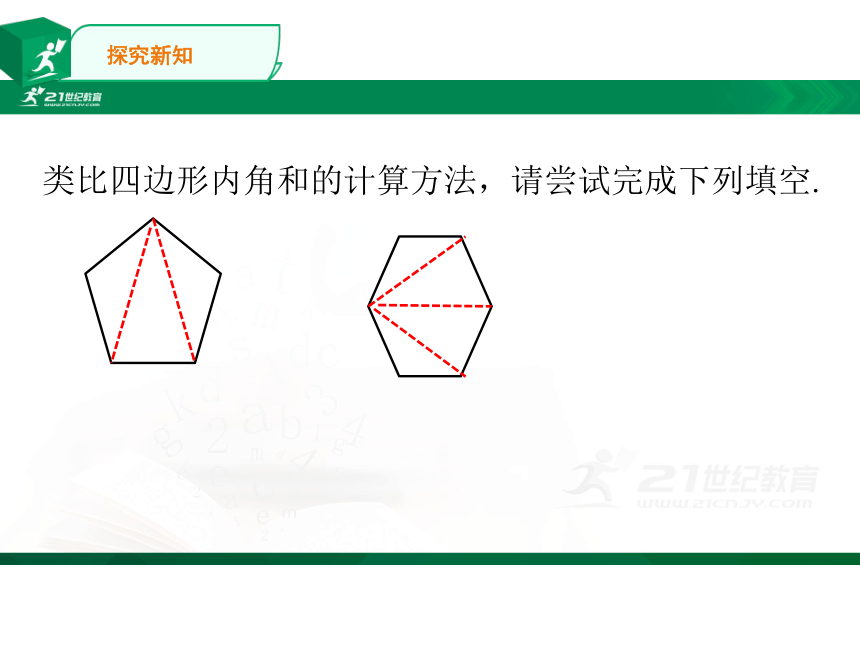
类比四边形内角和的计算方法,请尝试完成下列填空.
探究新知
从五边形的一个顶点出发,可以作出(
)条对角线,它们将五边形分成了(
)个三角形,五边形的内角和等于180°×(
).
从六边形的一个顶点出发,可以作出(
)条对角线,它们将六边形分成了(
)个三角形,六边形的内角和等于180°×(
).
2
3
3
4
4
3
探究新知
通过以上的探究,多边形的内角和与边数之间有密切的关系:
从n边形的一个顶点出发,
可以作出(n-3)条对角线,
它们将n边形分成了(n-2)个三角形,
n边形的内角和等于180°×(n-2).
多边形的内角和公式:n边形的内角和等于(n-2)×180°
探究新知
如果一个四边形的一组对角互补,那么另外一组对角有什么关系?
A
C
D
解:若在四边形ABCD中,∠A和∠C互补,
则∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=360°,
∴∠B+∠D=360
°-(∠A+∠C)=180°.
则∠B与∠D互为补角.
B
探究新知
n个外角加上与它们相邻的内角等于180°×n,
n边形的内角和为180°×(n-2),
n边形的外角和为180°×n-180°×(n-2)=360°.
性质:多边形的外角和等于360°。
探究新知
如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
A
B
C
D
E
F
1
2
3
5
4
6
分析:
1、六边形的每一个外角和相邻的内角有什么关系?
2、六边形的6个外角加上与它们相邻的内角,所得总和是多少?
3、上述总和与六边形的内角和、外角和有什么关系?
探究新知
A
B
C
D
E
F
1
2
3
5
4
6
3、上述总和与六边形的内角和、外角和有什么关系?
六个外角加上与它们相邻的内角等于180°×6=1080°,
六边形的内角和为180°×4=720°,
六边形的外角和为180°×6-180°×4=360°.
如果是n边形,会得出什么结论呢
探究新知
求出下列图形中x的值.
分析:(1)四边形的内角和为360°则x°+x°+140°+90°=360°
解得x=65.
(2)四边形的内角和为360°则1+75°+120°+80°=360°
解得∠1=85°因∠1+x°=180°所以x=95.
巩固练习
一个多边形的各内角都等于120°,它是几边形?
解:设这个多边形的边数为n,
因为各内角都等于120°,所以内角和120°×n.
由内角和公式得:120°
×n=(n-2)×
180°
解得n=6.
所以它是六边形.
巩固练习
一个多边形的内角和与外角和相等,它是几边形?
解:设这个多边形的边数为n,
由内角和公式得:(n-2)×180°
由外角和性质得:(n-2)×180°=360°
则360°
=(n-2)×180°
解得n=4.
所以它是四边形.
巩固练习
多边形的内角和
(n-2)×180°(n为≥3的整数)
外角和
多边形的外角和等于360°(与边数无关)
正多边形
内角=
外角=
课堂小结
(1)一个多边形的内角和是外角和的一半,则它是几边形?
解:因为多边形的外角和是360°,所以这个多边形的内角和为180°.内角和为180°的多边形是三角形.
或
内角和为(n-2)×180°,则(n-2)×180°=180°
解得n=3.
所以它是三角形.
课堂练习
(2)一个多边形的内角和是外角和的2倍,则它是几边形?
解:因为多边形的外角和是360°,所以这个多边形的内角和为720°.
内角和为(n-2)×180°,则(n-2)×
180°
=
720°
解得n=6.
所以它是六边形.
课堂练习
(3)已知一个多边形的每一个内角与其相邻外角的比都是7:2,则这个多边形是(
)边形,共有(
)条对角线.
九
27
课堂练习
解:设这个多边形的一个内角为7x°,则与其相邻的外角为2x°,
因为每一个内角与其相邻的外角之和为180°,所以7x°+2x°=
180°
,解得x=20,外角为40°.
边数为360°
÷40°
=9,则这个多边形是九边形.
对角线的条数为
课堂练习
https://www.21cnjy.com/help/help_extract.php
人教版
八年级上
多边形的内角和与外角和
1.了解并掌握多边形内角和与外角和公式.
2.理解多边形内角和与外角和公式的推导过程(重点)
3.灵活运用多边形的内角和与外角和定理解决实际问题.(难点)
学习目标
问题1:你能说出三角形的内角和是多少度吗?
三角形的内角和是180°
问题2:你知道长方形和正方形的内角和是多少度吗?
长方形和正方形的内角和都是360°
问题3:你能猜测任意一个四边形的内角和是多少度吗?
任意一个四边形的内角是360°
复习导入
请大家任意画一个四边形,用量角器量出四个内角的大小,并计算出四个内角的和是多少?
经过测量发现四边形的四个内角和为360°.
复习导入
A
B
D
C
如图,在四边形ABCD中,连接对角线AC,求四边形ABCD的内角和.
探究新知
解:∵对角线AC将四边形分为△ACD和△ACB,
∴在△ACD中,∠D+∠DAC+∠DCA=180°,
在△ACB中,∠B+∠BAC+∠BCA=180°.
∵∠D+∠DAC+∠DCA+∠B+∠BAC+∠BCA=360°,
∴∠D+∠DAB+∠B+∠BCD=360°.
∴四边形ABCD的内角和为360°..
探究新知
类比四边形内角和的计算方法,请尝试完成下列填空.
探究新知
从五边形的一个顶点出发,可以作出(
)条对角线,它们将五边形分成了(
)个三角形,五边形的内角和等于180°×(
).
从六边形的一个顶点出发,可以作出(
)条对角线,它们将六边形分成了(
)个三角形,六边形的内角和等于180°×(
).
2
3
3
4
4
3
探究新知
通过以上的探究,多边形的内角和与边数之间有密切的关系:
从n边形的一个顶点出发,
可以作出(n-3)条对角线,
它们将n边形分成了(n-2)个三角形,
n边形的内角和等于180°×(n-2).
多边形的内角和公式:n边形的内角和等于(n-2)×180°
探究新知
如果一个四边形的一组对角互补,那么另外一组对角有什么关系?
A
C
D
解:若在四边形ABCD中,∠A和∠C互补,
则∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=360°,
∴∠B+∠D=360
°-(∠A+∠C)=180°.
则∠B与∠D互为补角.
B
探究新知
n个外角加上与它们相邻的内角等于180°×n,
n边形的内角和为180°×(n-2),
n边形的外角和为180°×n-180°×(n-2)=360°.
性质:多边形的外角和等于360°。
探究新知
如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
A
B
C
D
E
F
1
2
3
5
4
6
分析:
1、六边形的每一个外角和相邻的内角有什么关系?
2、六边形的6个外角加上与它们相邻的内角,所得总和是多少?
3、上述总和与六边形的内角和、外角和有什么关系?
探究新知
A
B
C
D
E
F
1
2
3
5
4
6
3、上述总和与六边形的内角和、外角和有什么关系?
六个外角加上与它们相邻的内角等于180°×6=1080°,
六边形的内角和为180°×4=720°,
六边形的外角和为180°×6-180°×4=360°.
如果是n边形,会得出什么结论呢
探究新知
求出下列图形中x的值.
分析:(1)四边形的内角和为360°则x°+x°+140°+90°=360°
解得x=65.
(2)四边形的内角和为360°则1+75°+120°+80°=360°
解得∠1=85°因∠1+x°=180°所以x=95.
巩固练习
一个多边形的各内角都等于120°,它是几边形?
解:设这个多边形的边数为n,
因为各内角都等于120°,所以内角和120°×n.
由内角和公式得:120°
×n=(n-2)×
180°
解得n=6.
所以它是六边形.
巩固练习
一个多边形的内角和与外角和相等,它是几边形?
解:设这个多边形的边数为n,
由内角和公式得:(n-2)×180°
由外角和性质得:(n-2)×180°=360°
则360°
=(n-2)×180°
解得n=4.
所以它是四边形.
巩固练习
多边形的内角和
(n-2)×180°(n为≥3的整数)
外角和
多边形的外角和等于360°(与边数无关)
正多边形
内角=
外角=
课堂小结
(1)一个多边形的内角和是外角和的一半,则它是几边形?
解:因为多边形的外角和是360°,所以这个多边形的内角和为180°.内角和为180°的多边形是三角形.
或
内角和为(n-2)×180°,则(n-2)×180°=180°
解得n=3.
所以它是三角形.
课堂练习
(2)一个多边形的内角和是外角和的2倍,则它是几边形?
解:因为多边形的外角和是360°,所以这个多边形的内角和为720°.
内角和为(n-2)×180°,则(n-2)×
180°
=
720°
解得n=6.
所以它是六边形.
课堂练习
(3)已知一个多边形的每一个内角与其相邻外角的比都是7:2,则这个多边形是(
)边形,共有(
)条对角线.
九
27
课堂练习
解:设这个多边形的一个内角为7x°,则与其相邻的外角为2x°,
因为每一个内角与其相邻的外角之和为180°,所以7x°+2x°=
180°
,解得x=20,外角为40°.
边数为360°
÷40°
=9,则这个多边形是九边形.
对角线的条数为
课堂练习
https://www.21cnjy.com/help/help_extract.php
