人教版八年级上册第十一章 全等三角形
文档属性
| 名称 | 人教版八年级上册第十一章 全等三角形 |  | |
| 格式 | zip | ||
| 文件大小 | 317.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-13 10:12:45 | ||
图片预览






文档简介
(共22张PPT)
导航页
尾页
1. 教学目的
2. 新课导入
3. 新课讲解
全等三角形定义
全等三角形性质
全等三角形判定
6.习题巩固
7.小结
8.作业
首页
尾页
目的要求:
1、使学生理解判定两三角形全等的角边角公理,并能运用这个方法证明线段或角的相等。
2、通过画图发现公理,并用之解决问题。
重点难点:
1、重点:熟悉两三角形全等的定义、性质、判定。
2、难点:通过两个三角形全等,间接证明线段或角相等及两线平行、垂直等。
教学目的
导航页
新课导入
1、生活中有哪些能够完全重合的图形呢?
导航页
2、生活中有哪些能够完全重合的图形?
能够 重合的两个图形叫作
全等形
完全
导航页
互相重合的顶点叫作对应顶点
A D
B E
C F
互相重合的边叫作对应边
AB与DE
BC与EF
AC与DF
互相重合的角叫作对应角
∠A与∠D
∠B与∠E
∠C与∠F
能够完全重合的两个三角形叫作全等三角形
全等三角形定义
导航页
几何画板
下一页
A
B
C
E
D
F
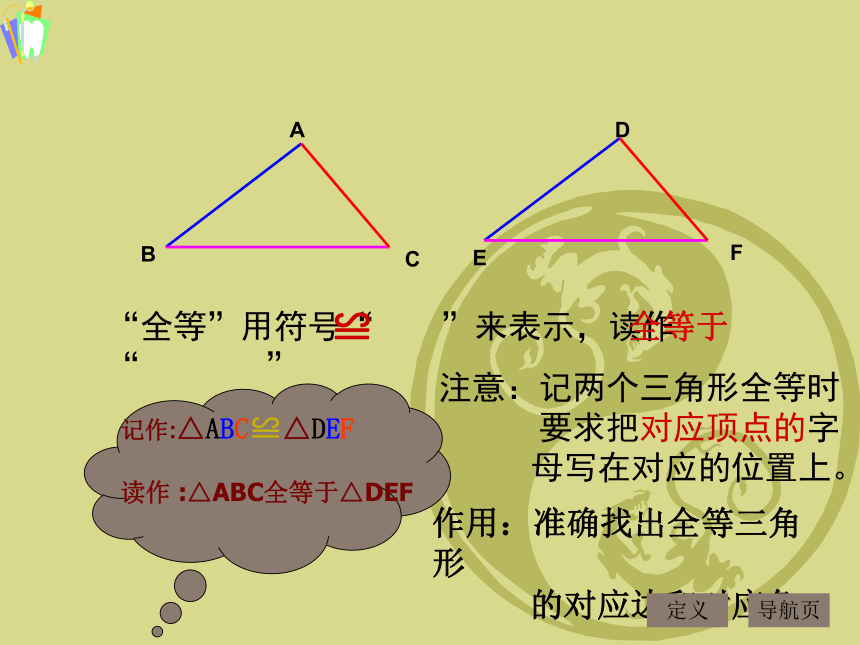
记作:△ABC≌△DEF
注意:记两个三角形全等时
要求把对应顶点的字
母写在对应的位置上。
“全等”用符号“ ”来表示,读作“ ”
≌
全等于
读作 :△ABC全等于△DEF
作用:准确找出全等三角形
的对应边和对应角。
导航页
定义
(全等三角形的对应角相等)
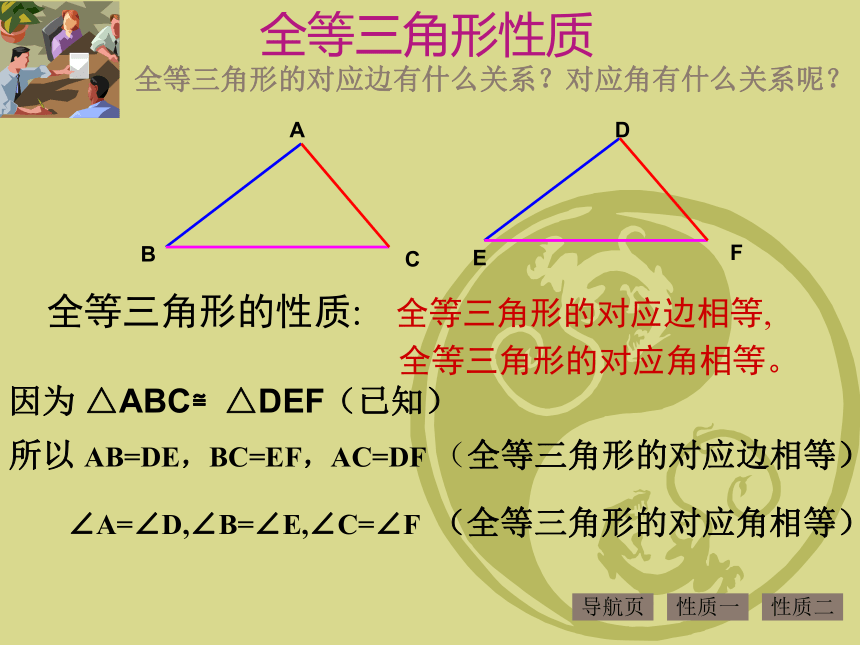
全等三角形的对应边相等,
全等三角形的对应角相等。
(已知)
(全等三角形的对应边相等)
所以 AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的性质:
因为 △ABC≌△DEF
E
D
F
A
B
C
全等三角形的对应边有什么关系?对应角有什么关系呢?
全等三角形性质
导航页
性质一
性质二
A
B
C
D
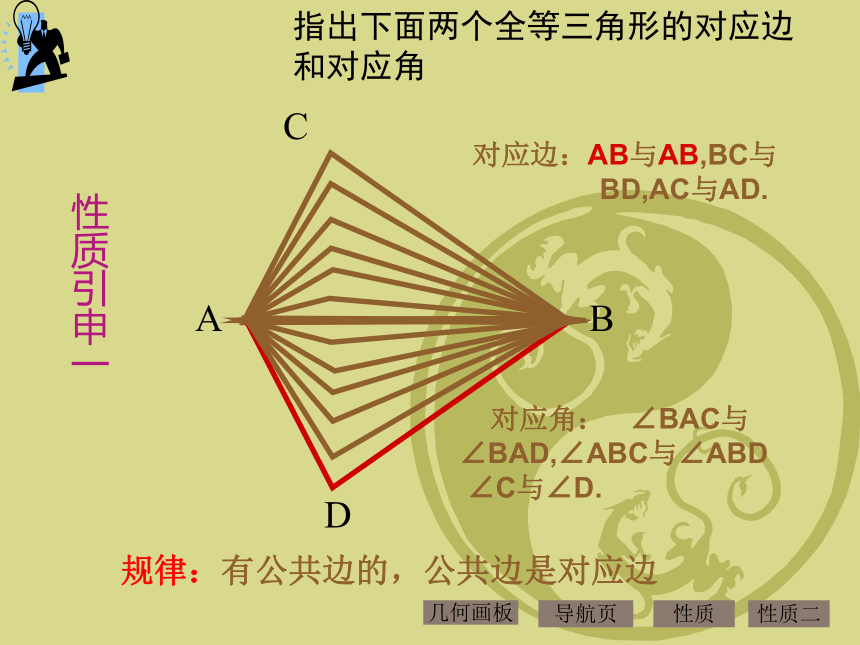
指出下面两个全等三角形的对应边
和对应角
对应边:AB与AB,BC与
BD,AC与AD.
对应角: ∠BAC与∠BAD,∠ABC与∠ABD
∠C与∠D.
规律:有公共边的,公共边是对应边
性质引申一
导航页
性质
性质二
几何画板
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;
(6)对应角所对的边是对应边,两个对应角所夹的边是对应边;
(7)对应边所对的角是对应角,两条对应边所夹的角是对应角;
(8)可根据全等式找对应边和对应角。
性质引申 二
导航页
性质
性质一
全等三角形的判定
一般三角形全等的判定:
SAS、ASA、AAS、SSS
直角三角形全等的判定:
SAS、ASA、AAS、SSS、HL
导航页
下一页
几何画板
三角形全等的识别的方法:
SSS:三条边对应相等的两个三角形全等。
SAS:有两条边和它们的夹角对应相等的两个三角形全等。
ASA: 有两个角和它们的夹边对应相等的两个三角形全等。
AAS: 有两个角和其中一个角的对边对应相等的两个
三角形全等。
(直角三角形)HL: 斜边及一条直角边对应相等的两个直角三角形
SSA:不能根据SSA判定是否全等
上一页
导航页
SSA画板
SSS
SAS
ASA
AAS
HL
2. 叫做全等三角形。
1.能够完全重合的两个图形叫做 。
全等形
4. 全等三角形的 相等; 相等
对应边
对应角
对应顶点
能够完全重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5. 在记两个三角形全等时要求把 写
在对应的位置上
全等于
≌
其中:互相重合的顶点叫做___
互相重合的边叫做___
互相重合的角叫做___
6.寻找对应元素的规律,准确找出全等三角 形的对应边和对应角。
对应顶点的字母
习题巩固
导航页
(SSS型).如图,AM=AN, BM=BN
说明△AMB≌△ANB的理由
解:在△AMB和△ANB中
∴ ≌ ( )
AN
已知
BM
AB
AB
△ABM
△ABN
SSS
SSS
导航页
小结
F
E
D
C
B
A
(SAS型).如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?
解:全等。∵BD=EC(已知)
∴BD-CD=EC-CD。即BC=ED
在△ABC与△FED中
∴△ABC≌△FED(SAS)
导航页
SAS
小结
(ASA型) 如图,∠1=∠2,∠3=∠4
求证:AC=AD
证明:∵∠ABD=180-∠3
∠ABC=180-∠4
而∠3=∠4(已知)
∴∠ABD=∠ABC
在△ABD和△ABC中
∠1=∠2(已知 )
AB=AB (公共边)
∠ABD=∠ABC (已知 )
∴△ABD ≌ △ABC(ASA )
∴AC=AD (全等三角形对应边相等)
1
2
3
4
导航页
ASA
小结
解:在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D (已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
1
2
导航页
AAS
(AAS型).已知,如图∠1=∠2, ∠C=∠D 求证:AC=AD
小结
(HL型)1. 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
解:在Rt△ACB和Rt△ADB中,有
AB=AB,
AC=AD.
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD
(全等三角形对应边相等).
导航页
小结
HL
导航页
小结归纳
作业
习题5.8:第1题
习题5.9:第1题
导航页
导航页
首页
导航页
尾页
1. 教学目的
2. 新课导入
3. 新课讲解
全等三角形定义
全等三角形性质
全等三角形判定
6.习题巩固
7.小结
8.作业
首页
尾页
目的要求:
1、使学生理解判定两三角形全等的角边角公理,并能运用这个方法证明线段或角的相等。
2、通过画图发现公理,并用之解决问题。
重点难点:
1、重点:熟悉两三角形全等的定义、性质、判定。
2、难点:通过两个三角形全等,间接证明线段或角相等及两线平行、垂直等。
教学目的
导航页
新课导入
1、生活中有哪些能够完全重合的图形呢?
导航页
2、生活中有哪些能够完全重合的图形?
能够 重合的两个图形叫作
全等形
完全
导航页
互相重合的顶点叫作对应顶点
A D
B E
C F
互相重合的边叫作对应边
AB与DE
BC与EF
AC与DF
互相重合的角叫作对应角
∠A与∠D
∠B与∠E
∠C与∠F
能够完全重合的两个三角形叫作全等三角形
全等三角形定义
导航页
几何画板
下一页
A
B
C
E
D
F
记作:△ABC≌△DEF
注意:记两个三角形全等时
要求把对应顶点的字
母写在对应的位置上。
“全等”用符号“ ”来表示,读作“ ”
≌
全等于
读作 :△ABC全等于△DEF
作用:准确找出全等三角形
的对应边和对应角。
导航页
定义
(全等三角形的对应角相等)
全等三角形的对应边相等,
全等三角形的对应角相等。
(已知)
(全等三角形的对应边相等)
所以 AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的性质:
因为 △ABC≌△DEF
E
D
F
A
B
C
全等三角形的对应边有什么关系?对应角有什么关系呢?
全等三角形性质
导航页
性质一
性质二
A
B
C
D
指出下面两个全等三角形的对应边
和对应角
对应边:AB与AB,BC与
BD,AC与AD.
对应角: ∠BAC与∠BAD,∠ABC与∠ABD
∠C与∠D.
规律:有公共边的,公共边是对应边
性质引申一
导航页
性质
性质二
几何画板
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;
(6)对应角所对的边是对应边,两个对应角所夹的边是对应边;
(7)对应边所对的角是对应角,两条对应边所夹的角是对应角;
(8)可根据全等式找对应边和对应角。
性质引申 二
导航页
性质
性质一
全等三角形的判定
一般三角形全等的判定:
SAS、ASA、AAS、SSS
直角三角形全等的判定:
SAS、ASA、AAS、SSS、HL
导航页
下一页
几何画板
三角形全等的识别的方法:
SSS:三条边对应相等的两个三角形全等。
SAS:有两条边和它们的夹角对应相等的两个三角形全等。
ASA: 有两个角和它们的夹边对应相等的两个三角形全等。
AAS: 有两个角和其中一个角的对边对应相等的两个
三角形全等。
(直角三角形)HL: 斜边及一条直角边对应相等的两个直角三角形
SSA:不能根据SSA判定是否全等
上一页
导航页
SSA画板
SSS
SAS
ASA
AAS
HL
2. 叫做全等三角形。
1.能够完全重合的两个图形叫做 。
全等形
4. 全等三角形的 相等; 相等
对应边
对应角
对应顶点
能够完全重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5. 在记两个三角形全等时要求把 写
在对应的位置上
全等于
≌
其中:互相重合的顶点叫做___
互相重合的边叫做___
互相重合的角叫做___
6.寻找对应元素的规律,准确找出全等三角 形的对应边和对应角。
对应顶点的字母
习题巩固
导航页
(SSS型).如图,AM=AN, BM=BN
说明△AMB≌△ANB的理由
解:在△AMB和△ANB中
∴ ≌ ( )
AN
已知
BM
AB
AB
△ABM
△ABN
SSS
SSS
导航页
小结
F
E
D
C
B
A
(SAS型).如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?
解:全等。∵BD=EC(已知)
∴BD-CD=EC-CD。即BC=ED
在△ABC与△FED中
∴△ABC≌△FED(SAS)
导航页
SAS
小结
(ASA型) 如图,∠1=∠2,∠3=∠4
求证:AC=AD
证明:∵∠ABD=180-∠3
∠ABC=180-∠4
而∠3=∠4(已知)
∴∠ABD=∠ABC
在△ABD和△ABC中
∠1=∠2(已知 )
AB=AB (公共边)
∠ABD=∠ABC (已知 )
∴△ABD ≌ △ABC(ASA )
∴AC=AD (全等三角形对应边相等)
1
2
3
4
导航页
ASA
小结
解:在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D (已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
1
2
导航页
AAS
(AAS型).已知,如图∠1=∠2, ∠C=∠D 求证:AC=AD
小结
(HL型)1. 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
解:在Rt△ACB和Rt△ADB中,有
AB=AB,
AC=AD.
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD
(全等三角形对应边相等).
导航页
小结
HL
导航页
小结归纳
作业
习题5.8:第1题
习题5.9:第1题
导航页
导航页
首页
