平行四边形的判定
图片预览



文档简介
(共14张PPT)
19.1平行四边形的判定(1)
九龙小学 唐渊
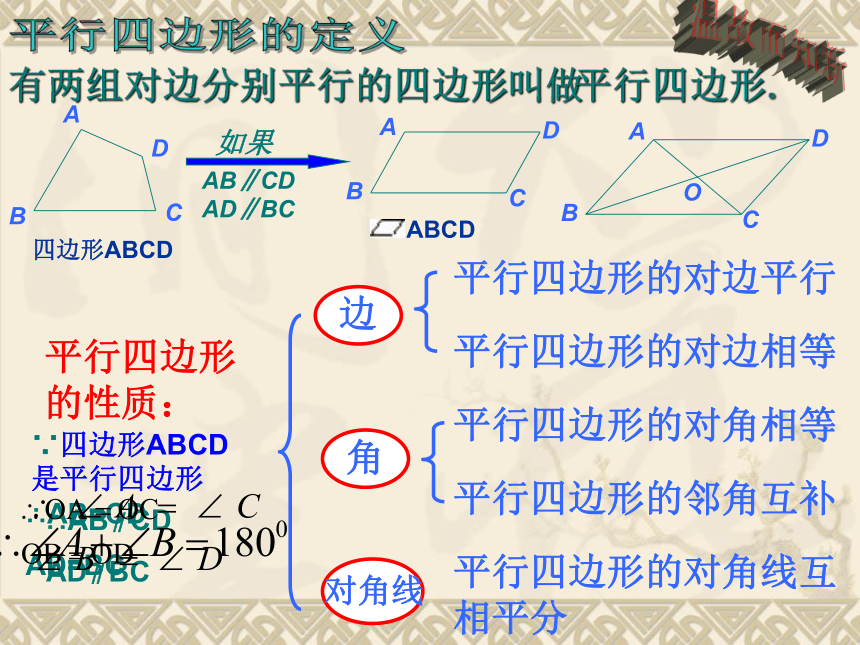
有两组对边分别平行的四边形
叫做
平行四边形。
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
如图,将两长两短的四根细竹条用小钉绞合在一起,做成一个四边形,请大家仔细观察,你得出的四边形是什么样的四边形。并说说你的理由。
大家齐动手
B
C
A
D
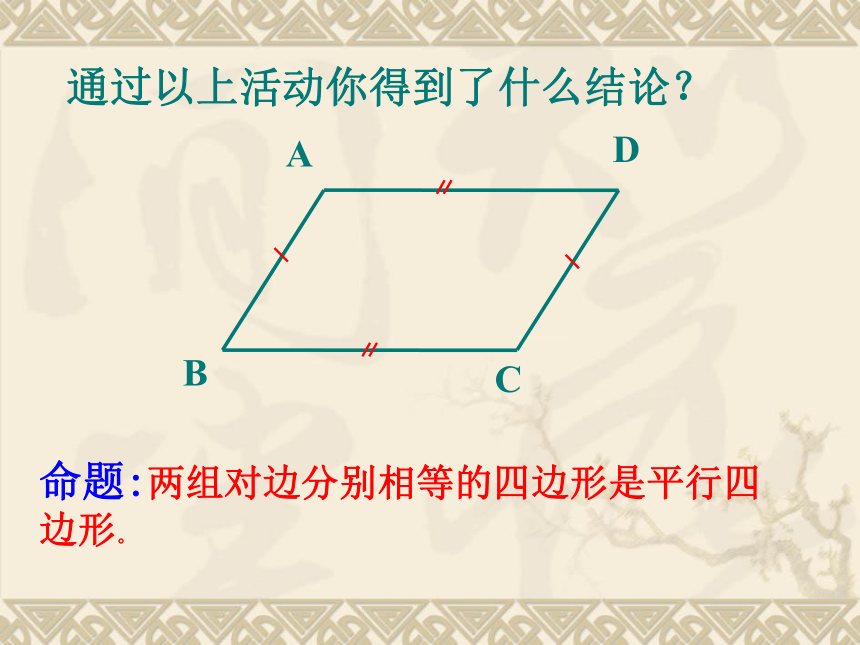
通过以上活动你得到了什么结论?
命题:两组对边分别相等的四边形是平行四边形。
探究:
已知:四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形。
分析:要证明一四边形是平行四边形,需要根据平行四边形的定义判断,即要证该四边形两组对边分别平行。
要证:四边形ABCD是平行四边形
AB∥ CD , AD∥ BC
连结AC。
AB=CD (已知)
AC=CA (公共边)
BC=DA(已知)
∴△ABC≌△CDA(SSS)
在△ABC和△CDA中,
∴ ∠1=∠3 , ∠ 2=∠4
∴AD∥ BC , AB∥ CD
∴四边形ABCD是平行四边形。
A
B
C
D
3
2
1
4
证明:
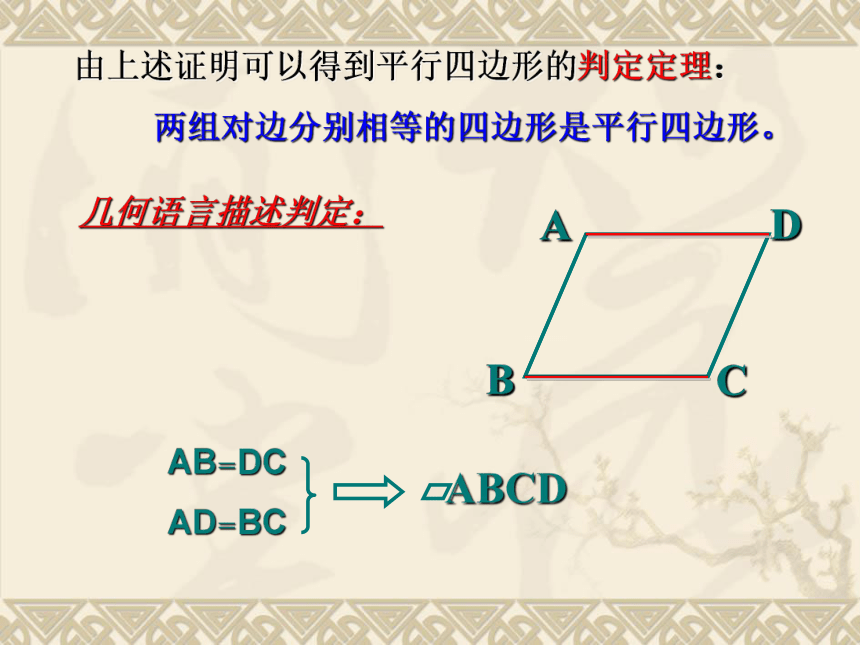
由上述证明可以得到平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形。
几何语言描述判定:
AB=DC
AD=BC
ABCD
A
B
C
D
A
B
C
D
如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
有两组对边分别平行的四边形
叫做
平行四边形。
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
对角线
A
D
C
B
求证:两组对角分别相等的四边形是平行四边形.
自主探索
已知:四边形ABCD中,∠A=∠C,∠B=∠D。
求证:四边形ABCD是平行四边形。
证明:在四边形ABCD中
∠A﹢∠B﹢∠C﹢∠D=360°
又∵∠A=∠C ∠B=∠D
∴ 2∠A﹢2∠B=360°
∴∠A﹢∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD为平行四边形。
A
D
C
B
已知:四边形ABCD中,AB∥CD,∠A=∠C。
自主探索
求证:四边形ABCD为平行四边形。
课堂小结
平行四边形的判定:
(一)两组对边分别平行的四边形是平行四边形。
(三)两组对角分别相等的四边形是平行四边形。
(二)两组对边分别相等的四边形是平行四边形。
如图,将两根细木条AC、BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,转动两根木条,它一直是一个平行四边形吗?你能证明吗?你又能得到什么结论?
动动手动动脑
谢谢大家﹗
再见﹗
19.1平行四边形的判定(1)
九龙小学 唐渊
有两组对边分别平行的四边形
叫做
平行四边形。
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
如图,将两长两短的四根细竹条用小钉绞合在一起,做成一个四边形,请大家仔细观察,你得出的四边形是什么样的四边形。并说说你的理由。
大家齐动手
B
C
A
D
通过以上活动你得到了什么结论?
命题:两组对边分别相等的四边形是平行四边形。
探究:
已知:四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形。
分析:要证明一四边形是平行四边形,需要根据平行四边形的定义判断,即要证该四边形两组对边分别平行。
要证:四边形ABCD是平行四边形
AB∥ CD , AD∥ BC
连结AC。
AB=CD (已知)
AC=CA (公共边)
BC=DA(已知)
∴△ABC≌△CDA(SSS)
在△ABC和△CDA中,
∴ ∠1=∠3 , ∠ 2=∠4
∴AD∥ BC , AB∥ CD
∴四边形ABCD是平行四边形。
A
B
C
D
3
2
1
4
证明:
由上述证明可以得到平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形。
几何语言描述判定:
AB=DC
AD=BC
ABCD
A
B
C
D
A
B
C
D
如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
有两组对边分别平行的四边形
叫做
平行四边形。
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
对角线
A
D
C
B
求证:两组对角分别相等的四边形是平行四边形.
自主探索
已知:四边形ABCD中,∠A=∠C,∠B=∠D。
求证:四边形ABCD是平行四边形。
证明:在四边形ABCD中
∠A﹢∠B﹢∠C﹢∠D=360°
又∵∠A=∠C ∠B=∠D
∴ 2∠A﹢2∠B=360°
∴∠A﹢∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD为平行四边形。
A
D
C
B
已知:四边形ABCD中,AB∥CD,∠A=∠C。
自主探索
求证:四边形ABCD为平行四边形。
课堂小结
平行四边形的判定:
(一)两组对边分别平行的四边形是平行四边形。
(三)两组对角分别相等的四边形是平行四边形。
(二)两组对边分别相等的四边形是平行四边形。
如图,将两根细木条AC、BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,转动两根木条,它一直是一个平行四边形吗?你能证明吗?你又能得到什么结论?
动动手动动脑
谢谢大家﹗
再见﹗
