北师大版四上3.4 《有趣的算式》课件(共10张PPT)
文档属性
| 名称 | 北师大版四上3.4 《有趣的算式》课件(共10张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 19:31:45 | ||
图片预览




文档简介
(共10张PPT)
在运算中,有很多有趣的算式,你们愿意同我们一起去探索吗?
同学们,让我们一起出发吧!别忘记带上你们的计算器。
111×111=
11×11=
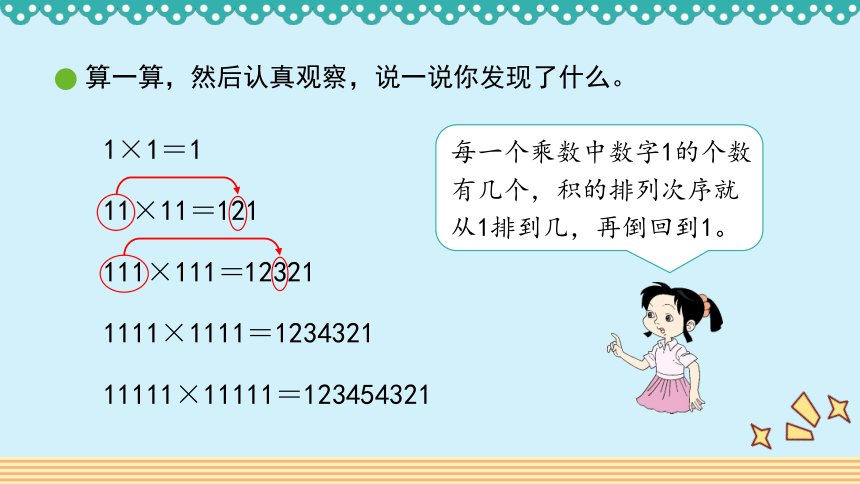
算一算,然后认真观察,说一说你发现了什么。
1×1=1
1111×1111=
1234321
11111×11111=
123454321
121
12321
每一个乘数中数字1的个数有几个,积的排列次序就从1排到几,再倒回到1。
写一写:你能继续写出两个这样的算式和结果么?
111111×111111=
1111111×1111111=
12345654321
1234567654321
不计算,你能直接写出下面算式的积吗?
99999×99999=?
999999×999999=?
从简单的算式开始,寻找规律。
快用计算器来试一试吧!
算一算:你能发现积有什么特点?
99×99=
999×999=
9999×9999=
9801
998001
99980001
如果算式中的两个乘数相同,且各数位上的数字都是9,那么积的前一部分比乘数少1,积的后一部分0的个数比乘数的位数少1,积的个位上是1。
99999×99999=
999999×999999=
9999800001
999998000001
观察下面的算式和得数分别有什么特点。
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=
12345×9+□=
123456×□+□=
11111
6
111111
9
7
1111111
在乘加算式中,如果第一个乘数是从1开始的连续自然数组成,第二个乘数是9,加上的数比第一个乘数的位数多1,则计算结果由若干个1组成,1的个数与算式中所加的数相同。
请用计算器算出这些算式的结果。
仔细观察积的特点,看看能不能发现什么?
142857×1=
142857×2=
142857×3=
142857×4=
142857
285714
428571
571428
1
4
2
8
7
5
积的首位数字是几,就是从这个数字开始,按顺时针方向将其余的数字按顺序写下来。
在0-9十个数字中,随意选出4个你喜欢的数字,将四个数字组成数字不重复的最大四位数和最小的四位数;
然后两数相减,并把得出的四位数重新组成一个最大的四位数与最小的数,再次相减……
这样不断重复的过程中,你会发现一个神秘的数,快来试一试,找一找吧!
8731
1378
-
7353
7533
3357
-
4176
7641
1467
-
6174
选择数字1、3、7、8
组数相减
得数重组
得数重组
6174
你还能举出其他的例子吗?
再见
!
在运算中,有很多有趣的算式,你们愿意同我们一起去探索吗?
同学们,让我们一起出发吧!别忘记带上你们的计算器。
111×111=
11×11=
算一算,然后认真观察,说一说你发现了什么。
1×1=1
1111×1111=
1234321
11111×11111=
123454321
121
12321
每一个乘数中数字1的个数有几个,积的排列次序就从1排到几,再倒回到1。
写一写:你能继续写出两个这样的算式和结果么?
111111×111111=
1111111×1111111=
12345654321
1234567654321
不计算,你能直接写出下面算式的积吗?
99999×99999=?
999999×999999=?
从简单的算式开始,寻找规律。
快用计算器来试一试吧!
算一算:你能发现积有什么特点?
99×99=
999×999=
9999×9999=
9801
998001
99980001
如果算式中的两个乘数相同,且各数位上的数字都是9,那么积的前一部分比乘数少1,积的后一部分0的个数比乘数的位数少1,积的个位上是1。
99999×99999=
999999×999999=
9999800001
999998000001
观察下面的算式和得数分别有什么特点。
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=
12345×9+□=
123456×□+□=
11111
6
111111
9
7
1111111
在乘加算式中,如果第一个乘数是从1开始的连续自然数组成,第二个乘数是9,加上的数比第一个乘数的位数多1,则计算结果由若干个1组成,1的个数与算式中所加的数相同。
请用计算器算出这些算式的结果。
仔细观察积的特点,看看能不能发现什么?
142857×1=
142857×2=
142857×3=
142857×4=
142857
285714
428571
571428
1
4
2
8
7
5
积的首位数字是几,就是从这个数字开始,按顺时针方向将其余的数字按顺序写下来。
在0-9十个数字中,随意选出4个你喜欢的数字,将四个数字组成数字不重复的最大四位数和最小的四位数;
然后两数相减,并把得出的四位数重新组成一个最大的四位数与最小的数,再次相减……
这样不断重复的过程中,你会发现一个神秘的数,快来试一试,找一找吧!
8731
1378
-
7353
7533
3357
-
4176
7641
1467
-
6174
选择数字1、3、7、8
组数相减
得数重组
得数重组
6174
你还能举出其他的例子吗?
再见
!
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
