苏科版七年级下第十一章图形的全等复习课件(13张)
文档属性
| 名称 | 苏科版七年级下第十一章图形的全等复习课件(13张) |  | |
| 格式 | zip | ||
| 文件大小 | 39.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-13 11:02:55 | ||
图片预览


文档简介
(共13张PPT)
你知道吗?
1、能够完全重合的图形叫做全等形。
2、两个能完全重合的三角形叫做全等三角形。
3、如果两个三角形全等,那么这两个三角形的对应边相等、对应角相等。
4、判定两个三角形全等的方法:
(1)SAS (2)ASA (3)AAS
(4)SSS (5)HL
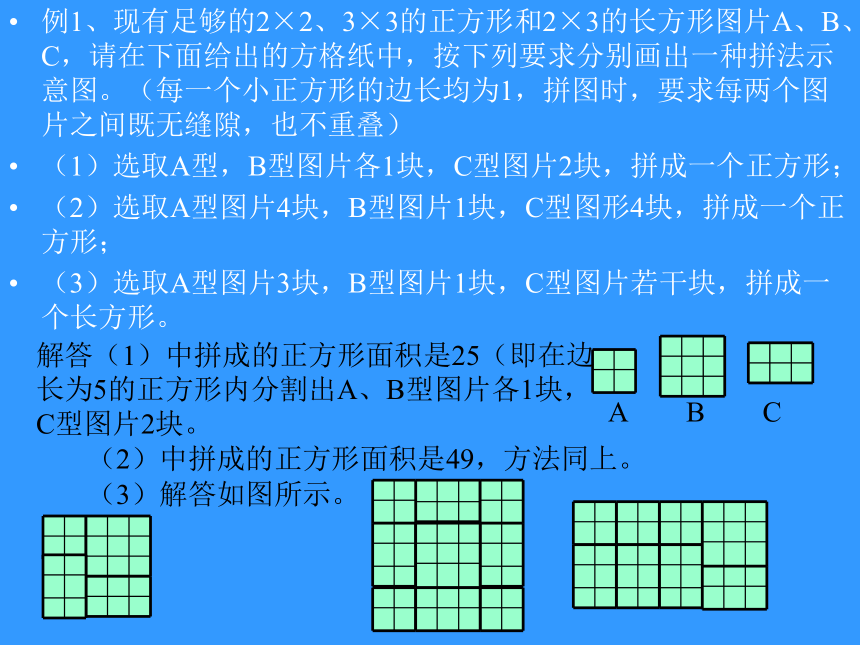
例1、现有足够的2×2、3×3的正方形和2×3的长方形图片A、B、C,请在下面给出的方格纸中,按下列要求分别画出一种拼法示意图。(每一个小正方形的边长均为1,拼图时,要求每两个图片之间既无缝隙,也不重叠)
(1)选取A型,B型图片各1块,C型图片2块,拼成一个正方形;
(2)选取A型图片4块,B型图片1块,C型图形4块,拼成一个正方形;
(3)选取A型图片3块,B型图片1块,C型图片若干块,拼成一个长方形。
解答(1)中拼成的正方形面积是25(即在边
长为5的正方形内分割出A、B型图片各1块,
C型图片2块。
A B C
(2)中拼成的正方形面积是49,方法同上。
(3)解答如图所示。
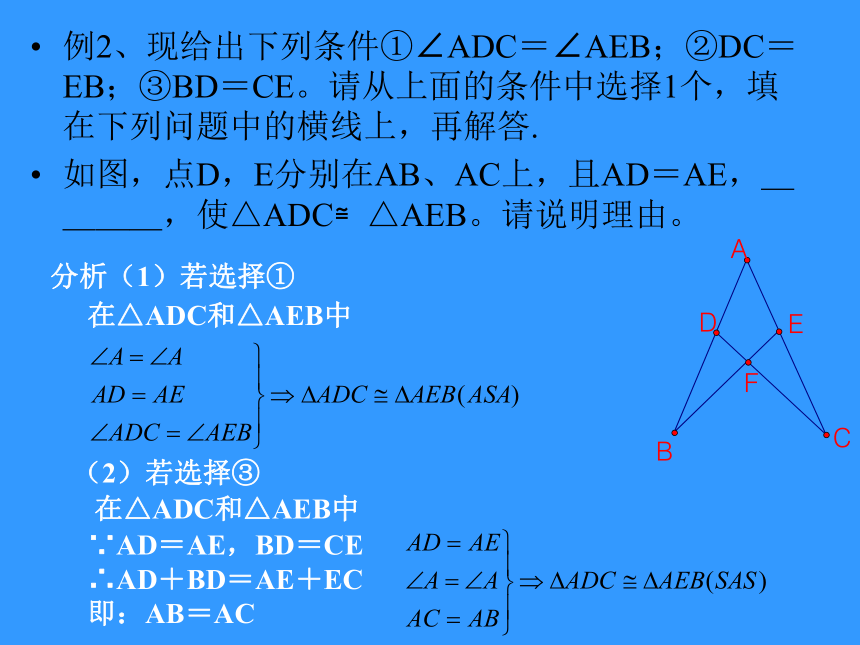
例2、现给出下列条件①∠ADC=∠AEB;②DC=EB;③BD=CE。请从上面的条件中选择1个,填在下列问题中的横线上,再解答.
如图,点D,E分别在AB、AC上,且AD=AE,____,使△ADC≌△AEB。请说明理由。
F
B
A
C
D
E
分析(1)若选择①
在△ADC和△AEB中
(2)若选择③
在△ADC和△AEB中
∵AD=AE,BD=CE
∴AD+BD=AE+EC
即:AB=AC
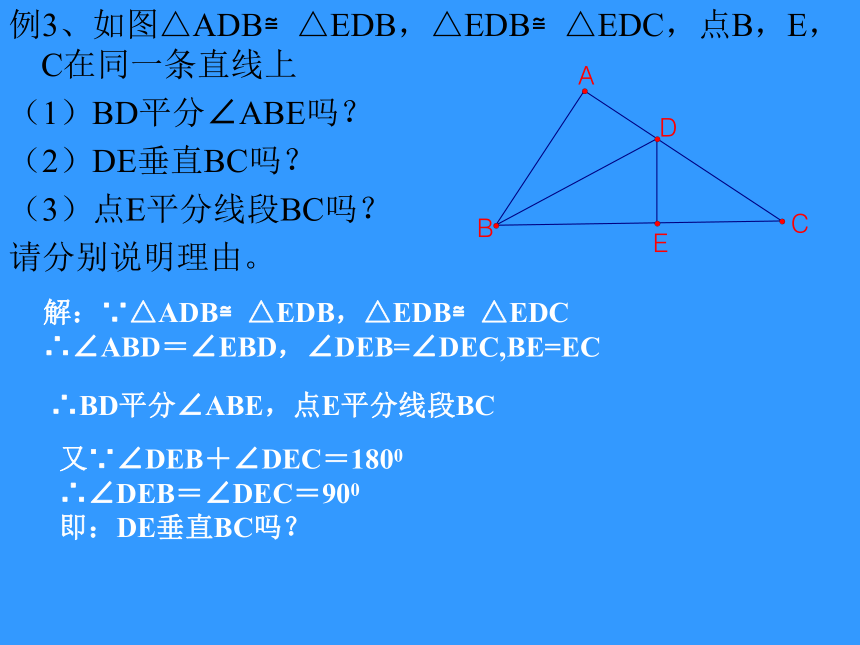
例3、如图△ADB≌△EDB,△EDB≌△EDC,点B,E,C在同一条直线上
(1)BD平分∠ABE吗?
(2)DE垂直BC吗?
(3)点E平分线段BC吗?
请分别说明理由。
解:∵△ADB≌△EDB,△EDB≌△EDC
∴∠ABD=∠EBD,∠DEB=∠DEC,BE=EC
∴BD平分∠ABE,点E平分线段BC
又∵∠DEB+∠DEC=1800
∴∠DEB=∠DEC=900
即:DE垂直BC吗?
例4、如图在6×6的方格纸中,我们把像△ABC这样顶点在网格上的三角形叫做格三角形。
(1)试在方格纸上画出与△ABC有
公共顶点,且全等的三角形;
(2)试在方格纸上画出与△ABC有
一条公共边,且全等的三角形;
(3)请计算一下与△ABC全等的格
点三角形的个数。
:
C
A
B
分析:几何图形的特征主要体现在它的形状、位置、大小。而本
题中的3个问题从点到边,再到位置层层递进,突出了分类思想,
也注重了数学学习方法的探索。
链接1
链接2
例5、如图,已知AB=AE,BC=ED,∠B=∠E,∠BAF=∠EAF,试说明AF⊥CD。
解答:连结AC、AD
在△ABC与△AED中
∵AB=AE
∠B=∠E
BC=ED
根据“SAS”
∴△ABC≌△AED
再根据“全等三角形对应边、
对应角相等”
∴AC=AD
∠BAC=∠EAD
又∵∠BAF=∠EAF
∴∠BAF-∠BAC=∠EAF-∠EAD
即:∠CAF=∠DAF
在△CAF与△DAF中
AC=AD
∠CAF=∠DAF
AF=AF(公共边)
根据“SAS”
∴△CAF≌△DAF
∴∠CFA=∠DFA
而∠CFA+∠DFA=1800
∴∠CFA=∠DFA=900
即:AF⊥CD
例6、全等三角形又叫合同三角形(如图),平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是合同三角形,且点A、B、C分别与点A1、B1、C1对应,当沿周界A→B→C →A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图1);若运动方向相反,则称它们是镜面合同三角形(如图2)。
两个真正合同三角形都可以要平面内通过平移或旋转使它们重合,而两个镜面合同三角形要重合,则必须将其中的一个翻转1800。下面各组合同三角形中,是镜面合同三角形的是( )
A B C D
B
例7、如图,在△ABC中,AD为BC边上的中线,试说明AB+AC与2AD之间的大小关系。
E
解:延长AD至E,使DE=AD
在△ABD与△ECD中
∵BD=DC(中线的定义)
∠ADB=∠EDC(对顶角相等)
AD=DE
∴△ABD≌△ECD(SAS)
根据全等三角形对应边相等
∴AB=EC
在△AEC中:AC+EC>AE
又∵AE=2AD
∴AB+AC>2AD
小结:对于三角形的中线,
我们可以通过延长中线的1
倍,来构造全等三角形。
联想:对于三角形的角平分
线,有时我们也可进行翻折
构造全等三角形。
例8、已知在△ABC中,AD是角平分线,且AC=AB+BD
试说明:∠B=2∠C
E
解:在AC上截取AE=AB,连结DE
在△AED与△ABD中
∵AE=AB
∠EAD=∠BAD(角平分线的定义)
AD=AD(公共边)
∴△AED≌△ABD(SAS)
根据全等三角形对应边、对应角相等
∴ED=BD,∠AED=∠B
又∵AC=AB+BD
∴CE=DE
根据等腰三角形的两个底角相等
∴∠C=∠EDC
又∵∠AED=∠C+∠EDC
∴∠AED=2∠C
∴∠B=2∠C
例9、传说在19世纪初,一位将军率领部队在一河边与敌军激战。为了使炮弹准确落到敌军阵地,将军面向敌军阵地的方向在河这岸站好,将帽子压低,使视线沿着帽沿恰好落在河对岸的边线上(如图)。然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上,接着,他用步测的方法量出自己与那个点的距离。将军说这个距离就是河的宽度。你能理解其中的道理吗?
解:在△ACD与△ABD中
∵∠CDA=∠BDA=900
AD=AD
∠CAD=∠BAD
∴△ACD≌△ABD(ASA)
根据全等三角形对应边相等
∴CD=BD
例10、如图,在四边形ABCD中,AD∥BC,∠ABC= ∠ DCB,AB=DC,AE=DF
(1)BF与CE相等吗?为什么?
(2)当E、F相向运动,形成图2时,BF与CE还相等吗?请说明理由。
(3)你认为当E、F运动时,还有几种与上述不同的图形?分别对BF与CE和关系加以说明。
解:∵AD∥BC
∴∠DAB+∠ABC=1800
∠ADC+∠DCB=1800
又∵∠ABC=∠DCB
∴∠DAB=∠ADC
又∵AE=DF
∴AE+AD=DF+AD
即ED=AF
在△EDC与△FAB中
∵ED=AF
∠EDC=∠FDB
DC=AB
∴△EDC≌△FAB(SAS)
∴BF=CE(全等三角形对应边相等)
同学们,这节课快结束了,通过学习你知道了什么呢?
你知道吗?
1、能够完全重合的图形叫做全等形。
2、两个能完全重合的三角形叫做全等三角形。
3、如果两个三角形全等,那么这两个三角形的对应边相等、对应角相等。
4、判定两个三角形全等的方法:
(1)SAS (2)ASA (3)AAS
(4)SSS (5)HL
例1、现有足够的2×2、3×3的正方形和2×3的长方形图片A、B、C,请在下面给出的方格纸中,按下列要求分别画出一种拼法示意图。(每一个小正方形的边长均为1,拼图时,要求每两个图片之间既无缝隙,也不重叠)
(1)选取A型,B型图片各1块,C型图片2块,拼成一个正方形;
(2)选取A型图片4块,B型图片1块,C型图形4块,拼成一个正方形;
(3)选取A型图片3块,B型图片1块,C型图片若干块,拼成一个长方形。
解答(1)中拼成的正方形面积是25(即在边
长为5的正方形内分割出A、B型图片各1块,
C型图片2块。
A B C
(2)中拼成的正方形面积是49,方法同上。
(3)解答如图所示。
例2、现给出下列条件①∠ADC=∠AEB;②DC=EB;③BD=CE。请从上面的条件中选择1个,填在下列问题中的横线上,再解答.
如图,点D,E分别在AB、AC上,且AD=AE,____,使△ADC≌△AEB。请说明理由。
F
B
A
C
D
E
分析(1)若选择①
在△ADC和△AEB中
(2)若选择③
在△ADC和△AEB中
∵AD=AE,BD=CE
∴AD+BD=AE+EC
即:AB=AC
例3、如图△ADB≌△EDB,△EDB≌△EDC,点B,E,C在同一条直线上
(1)BD平分∠ABE吗?
(2)DE垂直BC吗?
(3)点E平分线段BC吗?
请分别说明理由。
解:∵△ADB≌△EDB,△EDB≌△EDC
∴∠ABD=∠EBD,∠DEB=∠DEC,BE=EC
∴BD平分∠ABE,点E平分线段BC
又∵∠DEB+∠DEC=1800
∴∠DEB=∠DEC=900
即:DE垂直BC吗?
例4、如图在6×6的方格纸中,我们把像△ABC这样顶点在网格上的三角形叫做格三角形。
(1)试在方格纸上画出与△ABC有
公共顶点,且全等的三角形;
(2)试在方格纸上画出与△ABC有
一条公共边,且全等的三角形;
(3)请计算一下与△ABC全等的格
点三角形的个数。
:
C
A
B
分析:几何图形的特征主要体现在它的形状、位置、大小。而本
题中的3个问题从点到边,再到位置层层递进,突出了分类思想,
也注重了数学学习方法的探索。
链接1
链接2
例5、如图,已知AB=AE,BC=ED,∠B=∠E,∠BAF=∠EAF,试说明AF⊥CD。
解答:连结AC、AD
在△ABC与△AED中
∵AB=AE
∠B=∠E
BC=ED
根据“SAS”
∴△ABC≌△AED
再根据“全等三角形对应边、
对应角相等”
∴AC=AD
∠BAC=∠EAD
又∵∠BAF=∠EAF
∴∠BAF-∠BAC=∠EAF-∠EAD
即:∠CAF=∠DAF
在△CAF与△DAF中
AC=AD
∠CAF=∠DAF
AF=AF(公共边)
根据“SAS”
∴△CAF≌△DAF
∴∠CFA=∠DFA
而∠CFA+∠DFA=1800
∴∠CFA=∠DFA=900
即:AF⊥CD
例6、全等三角形又叫合同三角形(如图),平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是合同三角形,且点A、B、C分别与点A1、B1、C1对应,当沿周界A→B→C →A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图1);若运动方向相反,则称它们是镜面合同三角形(如图2)。
两个真正合同三角形都可以要平面内通过平移或旋转使它们重合,而两个镜面合同三角形要重合,则必须将其中的一个翻转1800。下面各组合同三角形中,是镜面合同三角形的是( )
A B C D
B
例7、如图,在△ABC中,AD为BC边上的中线,试说明AB+AC与2AD之间的大小关系。
E
解:延长AD至E,使DE=AD
在△ABD与△ECD中
∵BD=DC(中线的定义)
∠ADB=∠EDC(对顶角相等)
AD=DE
∴△ABD≌△ECD(SAS)
根据全等三角形对应边相等
∴AB=EC
在△AEC中:AC+EC>AE
又∵AE=2AD
∴AB+AC>2AD
小结:对于三角形的中线,
我们可以通过延长中线的1
倍,来构造全等三角形。
联想:对于三角形的角平分
线,有时我们也可进行翻折
构造全等三角形。
例8、已知在△ABC中,AD是角平分线,且AC=AB+BD
试说明:∠B=2∠C
E
解:在AC上截取AE=AB,连结DE
在△AED与△ABD中
∵AE=AB
∠EAD=∠BAD(角平分线的定义)
AD=AD(公共边)
∴△AED≌△ABD(SAS)
根据全等三角形对应边、对应角相等
∴ED=BD,∠AED=∠B
又∵AC=AB+BD
∴CE=DE
根据等腰三角形的两个底角相等
∴∠C=∠EDC
又∵∠AED=∠C+∠EDC
∴∠AED=2∠C
∴∠B=2∠C
例9、传说在19世纪初,一位将军率领部队在一河边与敌军激战。为了使炮弹准确落到敌军阵地,将军面向敌军阵地的方向在河这岸站好,将帽子压低,使视线沿着帽沿恰好落在河对岸的边线上(如图)。然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上,接着,他用步测的方法量出自己与那个点的距离。将军说这个距离就是河的宽度。你能理解其中的道理吗?
解:在△ACD与△ABD中
∵∠CDA=∠BDA=900
AD=AD
∠CAD=∠BAD
∴△ACD≌△ABD(ASA)
根据全等三角形对应边相等
∴CD=BD
例10、如图,在四边形ABCD中,AD∥BC,∠ABC= ∠ DCB,AB=DC,AE=DF
(1)BF与CE相等吗?为什么?
(2)当E、F相向运动,形成图2时,BF与CE还相等吗?请说明理由。
(3)你认为当E、F运动时,还有几种与上述不同的图形?分别对BF与CE和关系加以说明。
解:∵AD∥BC
∴∠DAB+∠ABC=1800
∠ADC+∠DCB=1800
又∵∠ABC=∠DCB
∴∠DAB=∠ADC
又∵AE=DF
∴AE+AD=DF+AD
即ED=AF
在△EDC与△FAB中
∵ED=AF
∠EDC=∠FDB
DC=AB
∴△EDC≌△FAB(SAS)
∴BF=CE(全等三角形对应边相等)
同学们,这节课快结束了,通过学习你知道了什么呢?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
