江西省智学联盟体2022届高三上学期8月第一次联考数学(文)试题 (Word版缺答案)
文档属性
| 名称 | 江西省智学联盟体2022届高三上学期8月第一次联考数学(文)试题 (Word版缺答案) |  | |
| 格式 | docx | ||
| 文件大小 | 199.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 17:32:29 | ||
图片预览

文档简介
2022届高三年级江西智学联盟体第一次联考
文科数学
试卷满分:150分
考试时长:120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
回答选择题时,选出每小题答案后,用2B铅笔把答題卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答橤标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结東后,将答题卡交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符题目要求的.
1.已知集合,则(
)
A.
B.
C.
D.
2.欧拉公式(为虚数单位)是由瑞士著名数学家欧拉发现的,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,在复变函数论里占有非常重要的地位.根据此公式,表示的复数在复平面内位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.已知命题
,则命题p的真假以及命题p的否定分别为(
)
A.假,
B.假,
C.真,
D.真,
5.白马寨是丰城市闻名遐迩的江西省历史文化名村,始建于南宋成淳九年,即公元1273年,是有名的江南望族.村子建筑布局讲究风水,全村六十四条巷道依据八卦图的演变程序而精心设计,没有一条直巷,隐含八卦图中六十四卦象,又为“聚财”之意.白马察至今完好地保存着125幢明清古建筑,成为吸引四方游客的一个旅游景区,我校高一年级周末准备用系统抽样的方法从1200名学生中抽取40人前往景区开展研学活动,现将1200名学生随机地从1~1200编号,按编号顺序平均分成40组(1~30号,31~60号,…,1171~1200号),若第4组与第6组抽出的号码之和为274,则第10组抽到的号码是(
)
A.272
B.274
C.287
D.296
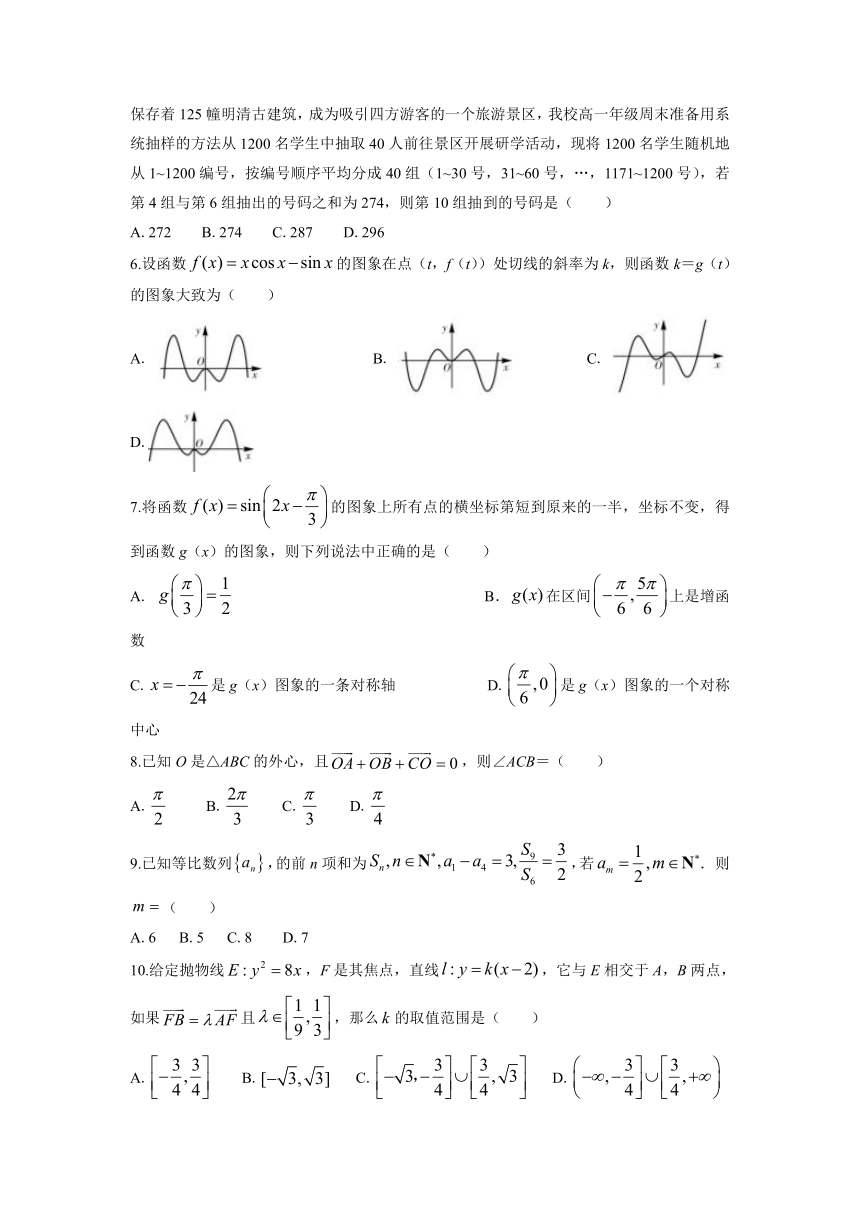
6.设函数的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的图象大致为(
)
A.
B.
C.
D.
7.将函数的图象上所有点的横坐标第短到原来的一半,坐标不变,得到函数g(x)的图象,则下列说法中正确的是(
)
A.
B.在区间上是增函数
C.是g(x)图象的一条对称轴 D.是g(x)图象的一个对称中心
8.已知O是△ABC的外心,且,则∠ACB=(
)
A.
B.
C.
D.
9.已知等比数列,的前n项和为,若
则(
)
A.6
B.5
C.8
D.7
10.给定抛物线,F是其焦点,直线,它与E相交于A,B两点,如果且,那么的取值范围是(
)
A.
B.
C.
D.
11.如图,三棱台ABC-A1B1C1中,AB⊥AC,BC=6,A1B1=A1C1=4,AA1=5,平面BCC1B1⊥平面ABC,则该三棱台外接球的体积为(
)
A.
B.
C.
D.
12.若关于x的不等式恒成立,则正数m的取值范围是(
)
A.
B.
C.
D.
二、填空題:本题共4小题,每小題5分,共20分.
13.若正项数列满足,则数列的通项公式是
.
14.祖冲之是我国南北朝时期杰出的数学家、天文学家.他一生钻研自然科学,其主要贡献在数学、天文历法和机械制造三方面,特别是在探索圆周率的精确度上,首次将“”精确到小数点后第七位,即=3,1415926…,在此基础上,我们从”圆周率”第三到第八位有效数字中随机取两个数字a,b,则事件“”的概率为
.
15.设f(x)是R上的可导函数,且,则f(2)的值为
.
16.已知双曲线
(a>0,b>0)的上、下焦点分别为F1,F2,过F1的直线交双曲线上支于A,B两点,且满足,则双曲线的离心率为
.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23題为选考題,考生根据要求作答.
(一)必考題:共60分.
17.(12分)已知△ABC中,角A,B,C的对边分别为a,b,c,且.
(1)求角A的大小;
(2)若a=3,求△ABC面积的最大值.
18.(12分)如图,直三棱柱ABC-A1B1C1中,D是AB的中点,AC=BC=3,AB=3,AA1=6.
(1)求证:AC1∥平面CDB1;
(2)求点C1到平面CDB1的距离.
19.(12分)根据世卫组织新冠肺炎疫情在线平台的数据,截至2021年6月18日,新冠肺炎全球确诊数已经超过17710万,新冠肺炎是一个传染性很强的疾病,其病毒在潜伏期内就具备了传染性.某医疗研究机构收集了1000名患者的病毒潜伏期的信息,将数据统计如下表所示:
潜伏期(单位:天)
人数
30
60
130
280
260
160
60
20
(1)求1000名患者潜伏期的样本平均数(同一组中的数据用该组区间的中点值作代表);
(2)潜伏期不高于平均数的患者,称为”短潜伏者”;潜伏期高于平均数的患者,称为”长潜伏者”.为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准分为两类进行分层抽样,从上述1000名患者中抽取400人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有99.9%的把握认为潜伏期长短与患者年龄有关.
短潜伏者
长潜伏者
合计
60岁及以上
100
60岁以下
150
合计
400
附表及公式:
0.10
0.05
0.010
0.001
2.706
3.841
6.635
10.828
20.(12分)已知函数有两个极值点x1,x2.
(1)求实数m的取值范围;
(2)证明:x1x2<4.
21.(12分)已知椭圆的离心率为,右焦点为F,且E上一点P到F的最大距离3.
(1)求椭圆E的方程;
(2)若A,B为椭圆E上的两点,线段AB过点F,且其垂直平分线交x轴于H点,,求.
(二)选考题:共10分.请考生在第2、23题中任选一题作答.如果多做,则按所作的第一题计分.
22.【选修4-4:坐标系与参数方程】(10分)
在直角坐标系中,直线的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求曲线C的直角坐标方程与直线的普通方程;
(2)直线与曲线C交于A,B两点,点P(4,-3),求
.
23.【选修4-5:不等式选讲】(10分)
设函数.
(1)当m=-1时,求不等式f(x)>9的解集;
(2)若,求m的取值范围.
文科数学
试卷满分:150分
考试时长:120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
回答选择题时,选出每小题答案后,用2B铅笔把答題卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答橤标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结東后,将答题卡交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符题目要求的.
1.已知集合,则(
)
A.
B.
C.
D.
2.欧拉公式(为虚数单位)是由瑞士著名数学家欧拉发现的,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,在复变函数论里占有非常重要的地位.根据此公式,表示的复数在复平面内位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.已知命题
,则命题p的真假以及命题p的否定分别为(
)
A.假,
B.假,
C.真,
D.真,
5.白马寨是丰城市闻名遐迩的江西省历史文化名村,始建于南宋成淳九年,即公元1273年,是有名的江南望族.村子建筑布局讲究风水,全村六十四条巷道依据八卦图的演变程序而精心设计,没有一条直巷,隐含八卦图中六十四卦象,又为“聚财”之意.白马察至今完好地保存着125幢明清古建筑,成为吸引四方游客的一个旅游景区,我校高一年级周末准备用系统抽样的方法从1200名学生中抽取40人前往景区开展研学活动,现将1200名学生随机地从1~1200编号,按编号顺序平均分成40组(1~30号,31~60号,…,1171~1200号),若第4组与第6组抽出的号码之和为274,则第10组抽到的号码是(
)
A.272
B.274
C.287
D.296
6.设函数的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的图象大致为(
)
A.
B.
C.
D.
7.将函数的图象上所有点的横坐标第短到原来的一半,坐标不变,得到函数g(x)的图象,则下列说法中正确的是(
)
A.
B.在区间上是增函数
C.是g(x)图象的一条对称轴 D.是g(x)图象的一个对称中心
8.已知O是△ABC的外心,且,则∠ACB=(
)
A.
B.
C.
D.
9.已知等比数列,的前n项和为,若
则(
)
A.6
B.5
C.8
D.7
10.给定抛物线,F是其焦点,直线,它与E相交于A,B两点,如果且,那么的取值范围是(
)
A.
B.
C.
D.
11.如图,三棱台ABC-A1B1C1中,AB⊥AC,BC=6,A1B1=A1C1=4,AA1=5,平面BCC1B1⊥平面ABC,则该三棱台外接球的体积为(
)
A.
B.
C.
D.
12.若关于x的不等式恒成立,则正数m的取值范围是(
)
A.
B.
C.
D.
二、填空題:本题共4小题,每小題5分,共20分.
13.若正项数列满足,则数列的通项公式是
.
14.祖冲之是我国南北朝时期杰出的数学家、天文学家.他一生钻研自然科学,其主要贡献在数学、天文历法和机械制造三方面,特别是在探索圆周率的精确度上,首次将“”精确到小数点后第七位,即=3,1415926…,在此基础上,我们从”圆周率”第三到第八位有效数字中随机取两个数字a,b,则事件“”的概率为
.
15.设f(x)是R上的可导函数,且,则f(2)的值为
.
16.已知双曲线
(a>0,b>0)的上、下焦点分别为F1,F2,过F1的直线交双曲线上支于A,B两点,且满足,则双曲线的离心率为
.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23題为选考題,考生根据要求作答.
(一)必考題:共60分.
17.(12分)已知△ABC中,角A,B,C的对边分别为a,b,c,且.
(1)求角A的大小;
(2)若a=3,求△ABC面积的最大值.
18.(12分)如图,直三棱柱ABC-A1B1C1中,D是AB的中点,AC=BC=3,AB=3,AA1=6.
(1)求证:AC1∥平面CDB1;
(2)求点C1到平面CDB1的距离.
19.(12分)根据世卫组织新冠肺炎疫情在线平台的数据,截至2021年6月18日,新冠肺炎全球确诊数已经超过17710万,新冠肺炎是一个传染性很强的疾病,其病毒在潜伏期内就具备了传染性.某医疗研究机构收集了1000名患者的病毒潜伏期的信息,将数据统计如下表所示:
潜伏期(单位:天)
人数
30
60
130
280
260
160
60
20
(1)求1000名患者潜伏期的样本平均数(同一组中的数据用该组区间的中点值作代表);
(2)潜伏期不高于平均数的患者,称为”短潜伏者”;潜伏期高于平均数的患者,称为”长潜伏者”.为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准分为两类进行分层抽样,从上述1000名患者中抽取400人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有99.9%的把握认为潜伏期长短与患者年龄有关.
短潜伏者
长潜伏者
合计
60岁及以上
100
60岁以下
150
合计
400
附表及公式:
0.10
0.05
0.010
0.001
2.706
3.841
6.635
10.828
20.(12分)已知函数有两个极值点x1,x2.
(1)求实数m的取值范围;
(2)证明:x1x2<4.
21.(12分)已知椭圆的离心率为,右焦点为F,且E上一点P到F的最大距离3.
(1)求椭圆E的方程;
(2)若A,B为椭圆E上的两点,线段AB过点F,且其垂直平分线交x轴于H点,,求.
(二)选考题:共10分.请考生在第2、23题中任选一题作答.如果多做,则按所作的第一题计分.
22.【选修4-4:坐标系与参数方程】(10分)
在直角坐标系中,直线的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求曲线C的直角坐标方程与直线的普通方程;
(2)直线与曲线C交于A,B两点,点P(4,-3),求
.
23.【选修4-5:不等式选讲】(10分)
设函数.
(1)当m=-1时,求不等式f(x)>9的解集;
(2)若,求m的取值范围.
同课章节目录
