2.1.1平面的基本性质
图片预览




文档简介
(共16张PPT)
一、复习:
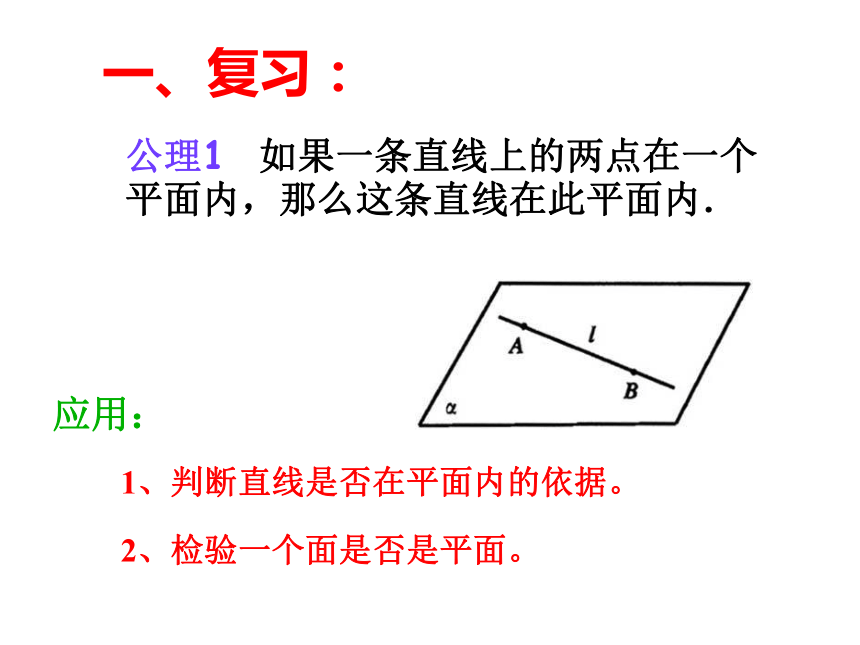
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
1、判断直线是否在平面内的依据。
应用:
2、检验一个面是否是平面。
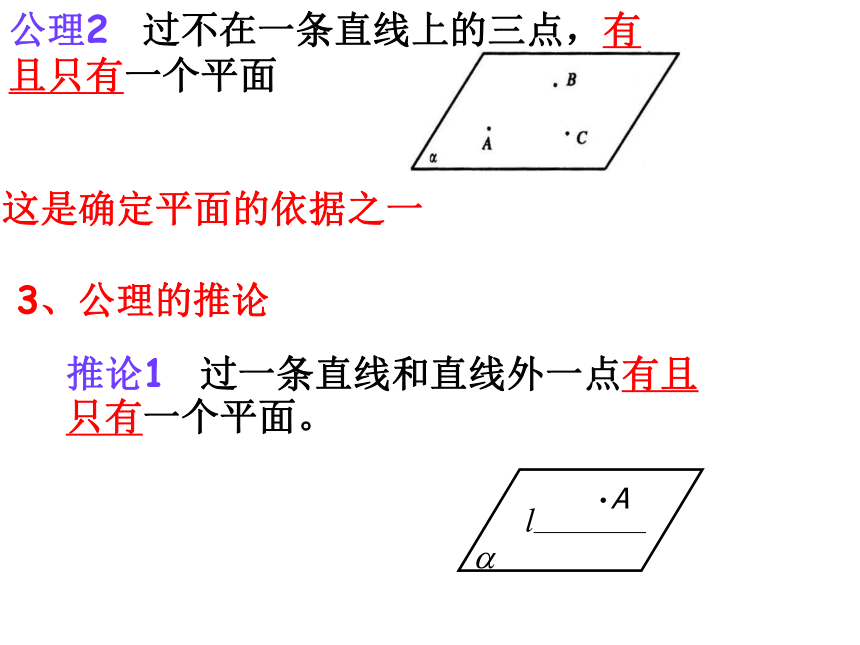
推论1 过一条直线和直线外一点有且只有一个平面。
公理2 过不在一条直线上的三点,有且只有一个平面
A
3、公理的推论
这是确定平面的依据之一
推论2 过两条相交直线有且只有一个平面。
推论3 过两条平行线有且只有一个平面 。
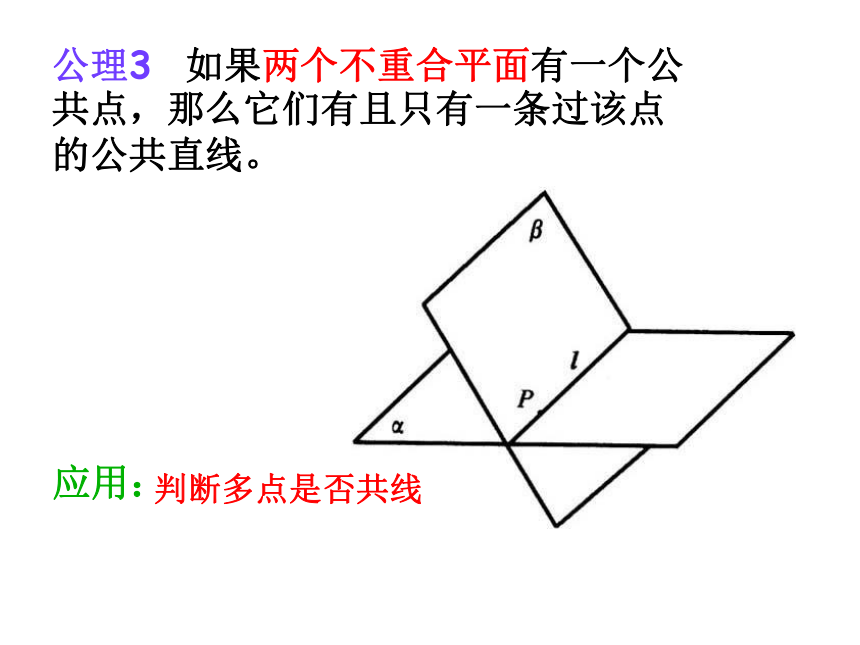
公理3 如果两个不重合平面有一个公共点,那么它们有且只有一条过该点的公共直线。
判断多点是否共线
应用:
几个概念:
平面图形
立体图形
空间图形
1.两个平面重合的条件是( )
A.有两个公共点 B.有无数个公共点
C.存在不共线的三个公共点 D.有一条公共直线
二、巩固练习:
2.下列命题中,正确的是( )
A.空间不同三点确定一个平面
B.空间两两相交的三条直线确定一个平面
C.两组对边相等的四边形是平行四边形
D.和同一直线都相交的三条平行线在同一平面内
3.空间有四个点,其中无三点共线,可确__________个平面.
4.一直线和直线外不在同一直线上的三点,最多可以确定几个平面?
1)直线AC1在平面CC1A1A内
2)由点A,O,C可以确定一个平面
由点A,C1,B1可以确定平面ADC1B1
三、例题:
例1、如图,已知三角形ABC在平面 外,
求证:PQR三点共线
A
B
P
R
Q
C
例2、正方体ABCD—A1B1C1D1中,AC1∩平面A1BD=M,求作点M。
本题体现了转化的思想,将在空间难以把握的线面交点转化为同一平面内的线线交点,确定了交点的位置。
A
D
C
B
C1
B1
A1
D1
例3.(1)正方体ABCD—A1B1C1D1中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状。
2如图,P,Q是正方体ABCD-A1B1C1D1的
棱AB,BC的中点,过P,Q,D1作一个平面,画
出此平面截正方体的截面.
A
B
C
D
A1
B1
C1
D1
P
Q
练习:求作下列截面:
A
D
C
B
C1
B1
A1
D1
A
D
C
B
C1
B1
A1
D1
练习:
一、复习:
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
1、判断直线是否在平面内的依据。
应用:
2、检验一个面是否是平面。
推论1 过一条直线和直线外一点有且只有一个平面。
公理2 过不在一条直线上的三点,有且只有一个平面
A
3、公理的推论
这是确定平面的依据之一
推论2 过两条相交直线有且只有一个平面。
推论3 过两条平行线有且只有一个平面 。
公理3 如果两个不重合平面有一个公共点,那么它们有且只有一条过该点的公共直线。
判断多点是否共线
应用:
几个概念:
平面图形
立体图形
空间图形
1.两个平面重合的条件是( )
A.有两个公共点 B.有无数个公共点
C.存在不共线的三个公共点 D.有一条公共直线
二、巩固练习:
2.下列命题中,正确的是( )
A.空间不同三点确定一个平面
B.空间两两相交的三条直线确定一个平面
C.两组对边相等的四边形是平行四边形
D.和同一直线都相交的三条平行线在同一平面内
3.空间有四个点,其中无三点共线,可确__________个平面.
4.一直线和直线外不在同一直线上的三点,最多可以确定几个平面?
1)直线AC1在平面CC1A1A内
2)由点A,O,C可以确定一个平面
由点A,C1,B1可以确定平面ADC1B1
三、例题:
例1、如图,已知三角形ABC在平面 外,
求证:PQR三点共线
A
B
P
R
Q
C
例2、正方体ABCD—A1B1C1D1中,AC1∩平面A1BD=M,求作点M。
本题体现了转化的思想,将在空间难以把握的线面交点转化为同一平面内的线线交点,确定了交点的位置。
A
D
C
B
C1
B1
A1
D1
例3.(1)正方体ABCD—A1B1C1D1中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状。
2如图,P,Q是正方体ABCD-A1B1C1D1的
棱AB,BC的中点,过P,Q,D1作一个平面,画
出此平面截正方体的截面.
A
B
C
D
A1
B1
C1
D1
P
Q
练习:求作下列截面:
A
D
C
B
C1
B1
A1
D1
A
D
C
B
C1
B1
A1
D1
练习:
