11.2全等三角形

11.2全等三角形
学习目标
1．知道全等三角形的意义，能正确找出全等三角形的对应顶点、对应角和对应边；
2．会用符号“≌”表示两个三角形全等；
3．经历平移、翻折、旋转等全等变换的过程，了解用图形变换识别全等三角形的方法；
4．让学生在探究性学习中体验学习的快乐，在合作交流中提高分析问题、解决问题能力，在小组竞争中培养团队精神．
学习难点
本节重点是三角形的性质， 难点是确认全等三角形的对应元素
教学过程
教材创设了一张明信片上盖有两个植树节纪念邮截的情景，使学生感受到数学和生活的联系．这一情景自然、贴切，有助于思维的展开，有助于兴趣的激发．
结合教学实际，我们还可以设计身边的其它情景．
情景1：为了组织春季体育节，现需制作形状和大小完全一样的三角形卡纸片若干张．七⑵班“翔宇”学习小组的8名同学每人制作了一张，其中只有一位同学制成的卡纸片不符合要求，如何把这张不符合要求的卡纸片区分开来 （该情景的好处是以学生感兴趣的问题为切入点，激发学生的学习兴趣，活跃课堂的气氛，培养学生的动手能力，让学生在做中轻松地学习数学知识，感受数学在生活中的应用）
情景2：①同底版等大的相片；②资料复印视频；③学生素质报告书上的印章……
说明:从我们身边的事、我们熟悉的情景出发，引出全等三角形的概念，自然、和谐，有利于学生学习兴趣的激发．
情景3：剪全等三角形。
剪两个能够完全重合的三角形并不困难，教师在活动中不要急于提示，更不要示范，以代替学生的活动．但在活动中教师要处理好以下几个方面的问题：
⑴要求学生课前准备好材料和工具；
⑵关注学生的不同剪法，但剪出的两个三角形必须重合；
⑶介绍全等三角形的一般记法，并学会如何在两个全等三角形上标注相等的角、边，理解对应的含义．
⑷全等三角形的意义：两个能重合的三角形是全等三角形．（这一过程完全由学生归纳，不一定一字不差．）
注:有条件的学校可以由几何画板演示，介绍对应顶点、对应角、对应边的概念．（让学生在理解对应元素的同时，形成全等变换的感受．）
问题1 由全等三角形的意义，你能发现哪些结论？
⑴学生容易想到的结论：①全等三角形的对应边相等；②全等三角形的对应角相等；
⑵学生可能想到的结论：（学生若未想到，可作简要说明）③全等三角形的面积相等；④全等三角形的周长相等；
⑶学生难归纳的结论：（抓住本质特征）⑤两个全等三角形，它们只是位置不同而已，其它特征（形状、大小）完全相同．
因此，我们用“△ABC≌△A′B′C′”表示△ABC和△A′B′C′全等．（为了突出顶点的对应，在表示全等时，我们总是把对应顶点的字母写在对应的位置上．）
这里，要求学生会模仿下列简单的说理过程:因为△ABC≌△A′B′C′，根据全等三角形的对应边相等，可以知道AB=A′B′，∠C＝∠C′.
问题2：先剪两个全等三角形纸片，再仔细体会全等三角形的意义：
⑴怎样表示这两个三角形全等？
⑵表示两个三角形全等时应该注意哪些问题？
⑶指出两个全等三角形的对应元素．
⑷若改变其中一张纸片的位置，比较上述问题，解答有无变化？
让学生探索可能出现的全等变换．
情景4： 图11.2-1， “做一做”把你做的两个三角形摆放成如下图的位置。
这个活动是为了帮助学生正确认识全等三角形而设计，教学中让学生按要求去做，认真观察两个三角形的位置变化，正确寻找全等三角形的对应顶点、对应边和对应角，在活动中理解旋转、平移、翻折的本质，活动按“操作—观察—作答”的顺序进行．根据学生的实际情况，让学生探索还有其它的摆法吗？
例题设计
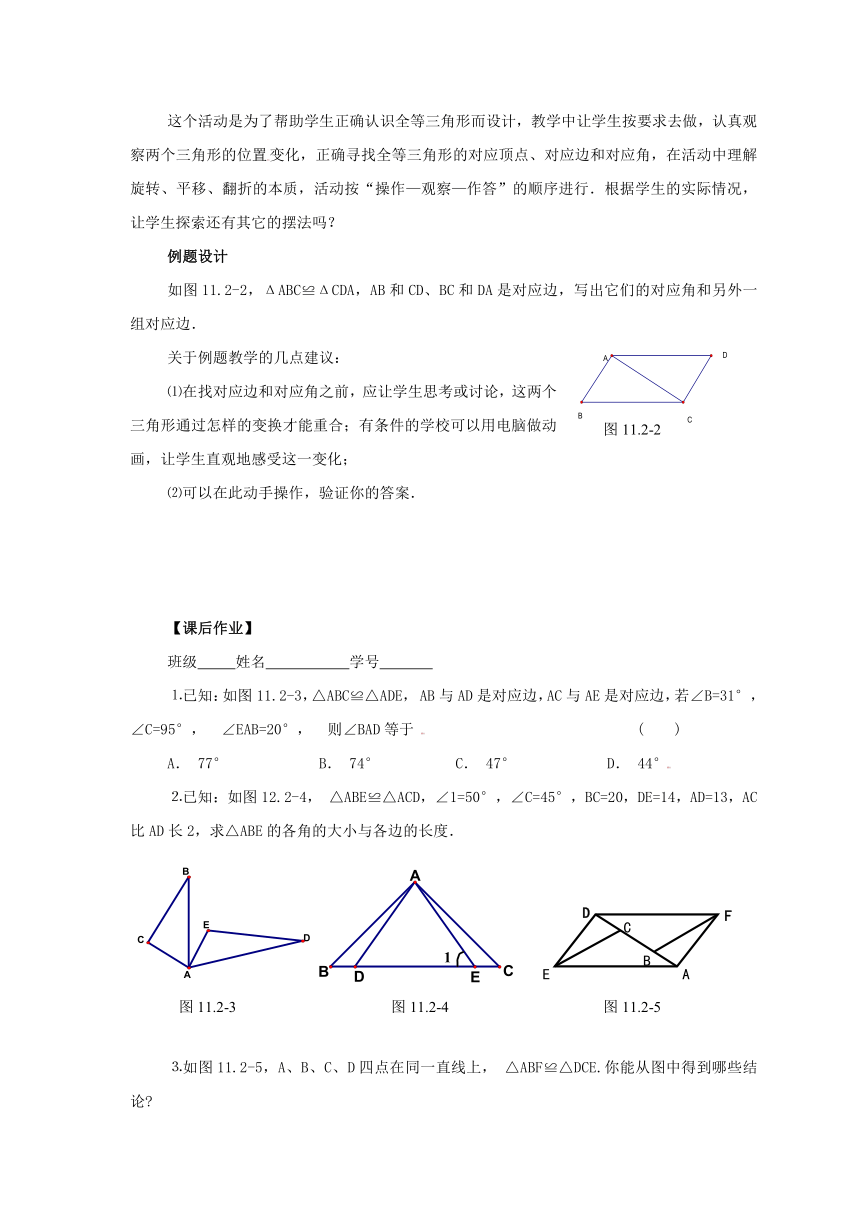
如图11.2-2，ΔABC≌ΔCDA，AB和CD、BC和DA是对应边，写出它们的对应角和另外一组对应边．
关于例题教学的几点建议：
⑴在找对应边和对应角之前，应让学生思考或讨论，这两个三角形通过怎样的变换才能重合；有条件的学校可以用电脑做动画，让学生直观地感受这一变化；
⑵可以在此动手操作，验证你的答案．
【课后作业】
班级 姓名 学号
⒈已知：如图11.2-3，△ABC≌△ADE， AB与AD是对应边，AC与AE是对应边，若∠B=31°， ∠C=95°， ∠EAB=20°， 则∠BAD等于 ( )
A． 77° B． 74° C． 47° D． 44°
⒉已知：如图12.2-4， △ABE≌△ACD，∠1=50°，∠C=45°，BC=20，DE=14，AD=13，AC比AD长2，求△ABE的各角的大小与各边的长度．
⒊如图11.2-5，A、B、C、D四点在同一直线上， △ABF≌△DCE.你能从图中得到哪些结论
说明：这几道练习的设置，一方面训练学生对几种全等变换的认识，正确识别全等图形，另一方面让学生学会寻找间接条件，用较为规范的几何语言进行说理.
4．已知图11.2-6中的2个三角形全等，则可记为△ABC≌△F______，其中点A的对应顶点是_______，边BC的对应边是______，∠ACB的对应角是_______．
图11.2-6 图11.2-7 图11.2-8
5．在图11.2-7中的一副七巧板中，试找出全等的三角形．
6．如图11.2-8，△ABC≌△ADE．你能否只通过一次变换（旋转、翻折、平移），使△ABC与△ADE重合？试写出对应边和对应角．
7．如图，△FCE是△ABD沿BD所在直线平移而得到的．请找出图中的全等三角形，若∠B=30°，∠BAD=90°，求△FCE各内角的度数．
8．如图，在一张长方形纸片上，作AB∥DC，并沿着AB、DC剪开，可剪出一个平行四边形ABCD，再沿着线段AC翻折，平行四边形被折痕分成了2个三角形，它们全等吗？可以沿AC剪开来检验，这时，图中有哪些相等的线段和角？
9．如图，△ABC中，AB=AC=4cm，∠B=60°，D是BC的中点，连接AD，那么△ABD与△ACD能重合吗？你能确定△ACD中哪些角的大小，哪些边的长度？
11．如图，△ABC≌△ADE，∠B=30°，∠C=60°，BC=3cm，你能确定△ADE中哪些角的大小，哪些边的长度？
12．如图，△ABC≌△DEF，B与E、C与F是对应顶点．问进行怎样的图形变换可以使这两个三角形重合？
A
B
E
C
F
D
A
B
C
D
E
A
B
C
E
F
P
M
N
F
E
A
B
C
D
F
E
（图①）
（图②）
（图③）
（图④）
（图⑤）
O
图11.2-1
图11.2-2
图11.2-3
1
D
A
B
F
E
C
图11.2-4
图11.2-5