华师大版数学九年级上册23.1.2平行线分线段成比例课件(共21张PPT)
文档属性
| 名称 | 华师大版数学九年级上册23.1.2平行线分线段成比例课件(共21张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 11:22:47 | ||
图片预览






文档简介
(共21张PPT)
l1
A
B
C
D
E
F
l2
l3
23.1.2
平行线分线段成比例
1.
什么是成比例线段?判断四条线段成比例的步骤是什么?
2.比例的基本性质是什么?
1.理解“平行线分线段成比例”的基本事实及“平行线分三角形两边成比例”的性质,并会灵活应用.
2.通过对基本事实的探究,进一步培养类比的数学思想.
探究(一)
l1
l2
l3
A
B
C
线段AB
与
线段BC的数量关系?
直线被间距相等的三条平行线截得的线段间数量关系
AB=BC
A1
B1
C1
A1B1=B1C1
m
n
探究(二)
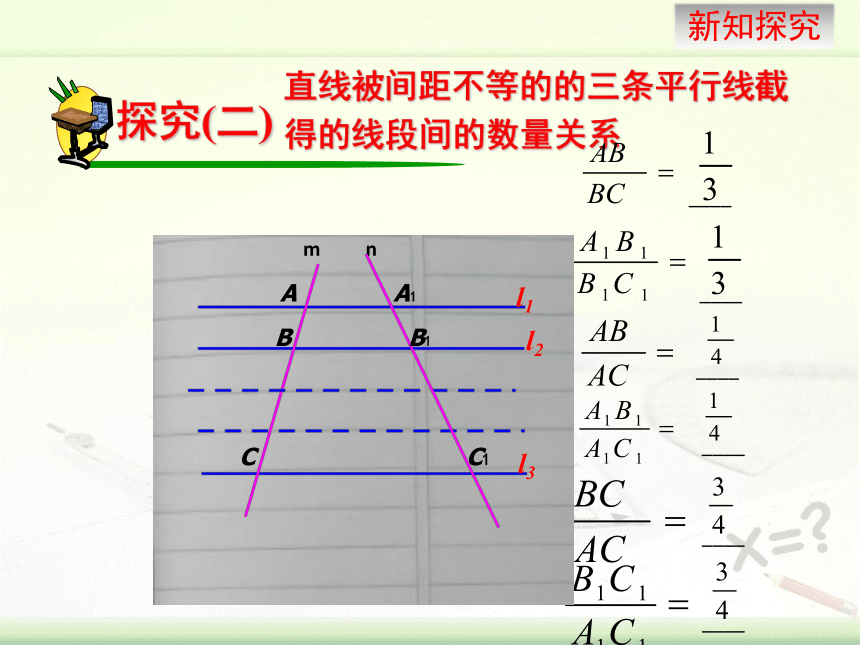
直线被间距不等的的三条平行线截得的线段间的数量关系
A
B
C
A1
B1
C1
l1
l2
l3
____
____
____
____
____
____
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
探究(二)
A
B
C
A1
B1
C1
l1
l2
l3
进而得出:
=
=
=
平行线分线段成比例基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。
几何语言
∵直线l1∥l2∥l3
∴
A
B
C
A1
B1
C1
l1
l2
l3
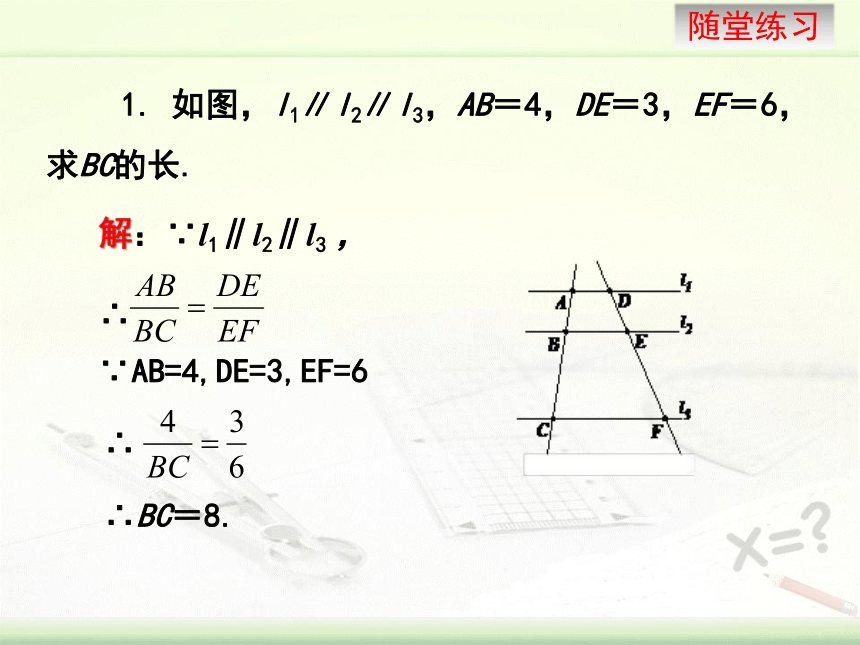
1.
如图,l1∥l2∥l3,AB=4,DE=3,EF=6,求BC的长.
解:∵l1∥l2∥l3
,
∴
∵AB=4,DE=3,EF=6
∴
∴BC=8.
l1
l2
l3
m
n
A
D
B
C
E
F
n
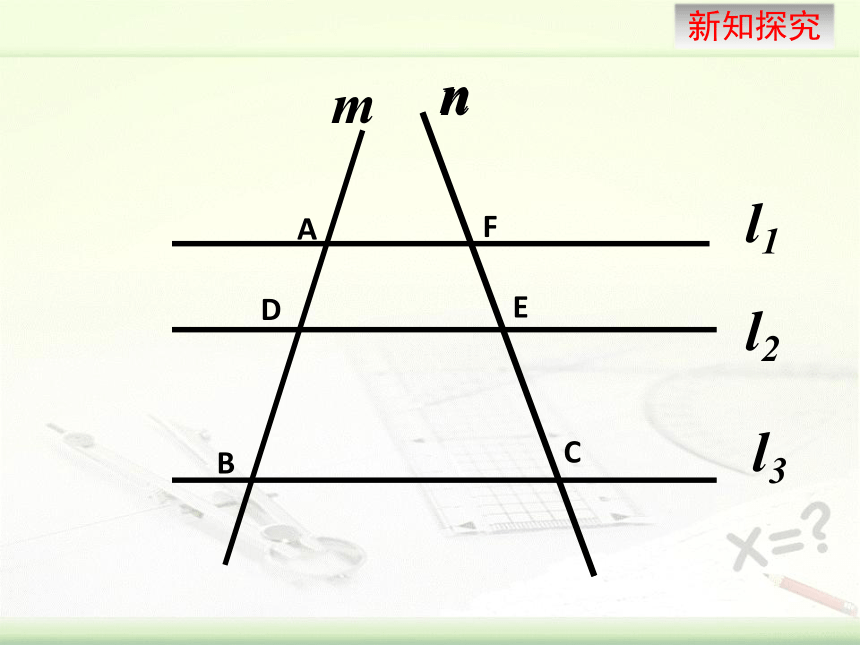
几何语言
A
B
C
D
E
∵DE∥BC,
A型图
l1
l2
l3
m
n
D
A
B
C
F
E
n
∵DE∥BC,
几何语言
A
B
C
E
D
X型图
平行线分三角形两边成比例:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
几何语言:
∵
DE∥BC,
A
B
C
D
E
A
B
C
E
D
1、判断题:
如图:DE∥BC,
下列各式是否正确:
A
B
C
D
E
2、填空题:
如图:DE∥BC,已知
则
A
B
C
E
D
做一做
教材p53
已知:DE//AF//BC,找出图中成比例的线段。
3.如图,E为□ABCD的边CD延长线上的一点,连结BE,交AC于点O,交AD于点F,求证:
一、平行线分线段成比例基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。(关键要能熟练地找出对应线段)
二、该基本事实在三角形中的应用:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
作业:
1.完成课本P54读一读;
2.课本P55练习题1,2题。
谢谢!
1、如图:
已知
DE∥BC,
AB
=
14,
AC
=
18,AE
=
10,
求:AD的长。
A
B
C
D
E
A
B
D
C
E
2、如图:
已知AB⊥BD,
ED⊥BD,垂足分别为B、D。求证
课后练习
3、如图:
已知
DE∥BC,
AB
=
5,
AC
=
7,AD=
2.
求:AE的长。
A
B
C
D
E
l1
A
B
C
D
E
F
l2
l3
23.1.2
平行线分线段成比例
1.
什么是成比例线段?判断四条线段成比例的步骤是什么?
2.比例的基本性质是什么?
1.理解“平行线分线段成比例”的基本事实及“平行线分三角形两边成比例”的性质,并会灵活应用.
2.通过对基本事实的探究,进一步培养类比的数学思想.
探究(一)
l1
l2
l3
A
B
C
线段AB
与
线段BC的数量关系?
直线被间距相等的三条平行线截得的线段间数量关系
AB=BC
A1
B1
C1
A1B1=B1C1
m
n
探究(二)
直线被间距不等的的三条平行线截得的线段间的数量关系
A
B
C
A1
B1
C1
l1
l2
l3
____
____
____
____
____
____
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
n
A
B
C
A1
B1
C1
l1
l2
l3
m
探究(二)
A
B
C
A1
B1
C1
l1
l2
l3
进而得出:
=
=
=
平行线分线段成比例基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。
几何语言
∵直线l1∥l2∥l3
∴
A
B
C
A1
B1
C1
l1
l2
l3
1.
如图,l1∥l2∥l3,AB=4,DE=3,EF=6,求BC的长.
解:∵l1∥l2∥l3
,
∴
∵AB=4,DE=3,EF=6
∴
∴BC=8.
l1
l2
l3
m
n
A
D
B
C
E
F
n
几何语言
A
B
C
D
E
∵DE∥BC,
A型图
l1
l2
l3
m
n
D
A
B
C
F
E
n
∵DE∥BC,
几何语言
A
B
C
E
D
X型图
平行线分三角形两边成比例:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
几何语言:
∵
DE∥BC,
A
B
C
D
E
A
B
C
E
D
1、判断题:
如图:DE∥BC,
下列各式是否正确:
A
B
C
D
E
2、填空题:
如图:DE∥BC,已知
则
A
B
C
E
D
做一做
教材p53
已知:DE//AF//BC,找出图中成比例的线段。
3.如图,E为□ABCD的边CD延长线上的一点,连结BE,交AC于点O,交AD于点F,求证:
一、平行线分线段成比例基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。(关键要能熟练地找出对应线段)
二、该基本事实在三角形中的应用:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
作业:
1.完成课本P54读一读;
2.课本P55练习题1,2题。
谢谢!
1、如图:
已知
DE∥BC,
AB
=
14,
AC
=
18,AE
=
10,
求:AD的长。
A
B
C
D
E
A
B
D
C
E
2、如图:
已知AB⊥BD,
ED⊥BD,垂足分别为B、D。求证
课后练习
3、如图:
已知
DE∥BC,
AB
=
5,
AC
=
7,AD=
2.
求:AE的长。
A
B
C
D
E
