23.1.2平行线分线段成比例 华师大版数学九年级上册 课件(共17张PPT)
文档属性
| 名称 | 23.1.2平行线分线段成比例 华师大版数学九年级上册 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 00:00:00 | ||
图片预览






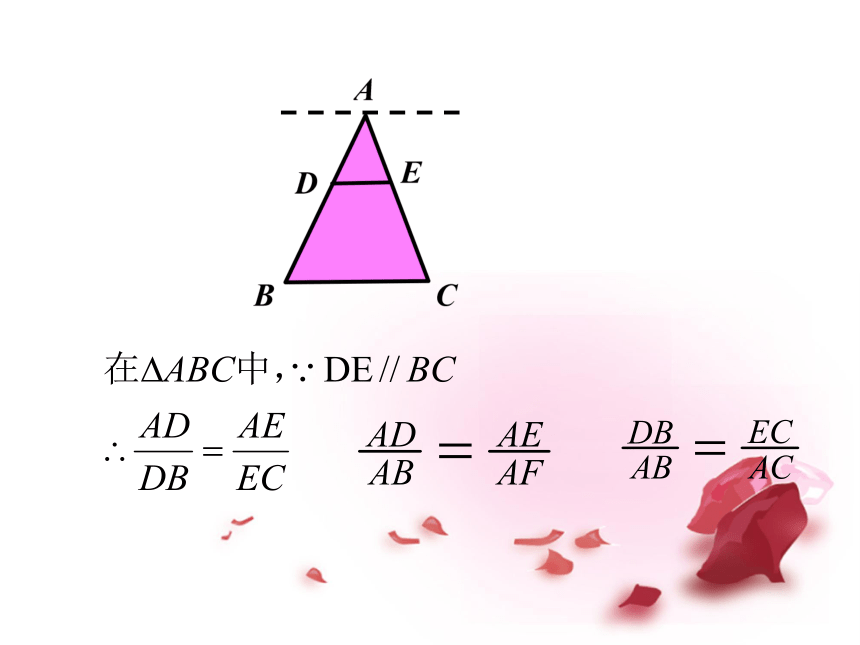
文档简介
(共17张PPT)
华东师大版九年数学上册
作业本里的小秘密?
A
B
C
测量线段AB和线段BC的长度,你们发现什么?
小组合作探究:
在作业本上任意画一条直线m,与相邻的三条平行线交于A、B、C三点,得到两条线段AB、BC.
m
AB=BC
n
D
E
F
DE
EF
=
所以我们
可以得到
=
=
做一做
选择作业本上不相邻的三条平行线
A
D
B
F
E
C
m
n
指出
AD、DB、FE、EC这四条线段的长度有什么关系?
我们发现:
思考:我们还可以发现哪些线段成比例?
两条直线被一组平行线所截,所得的对应线段
成比例(简称平行线分线段成比例)
F
E
C
A
D
B
几何语言:
想一想,从图中你还能得出哪些线段成比例线段?
思考1:当A点与F点重合时,就成了一个三角形的特殊情形,此时AD、DB、AE、EC这四条线段之间会有怎样的关系呢?
A
D
B
F
E
C
A
D
B
(F)
E
C
结论:
A
F
D
A
F
思考2:如图当直线m、n相交于第二条平行线上某点时,是否也有类似的成比例线段呢?
我们发现结论:
m
B
A
D
n
E
C
几何符号语言
推论:
平行于三角形一边的直线
截其他两边(或两边的延长
线),所得的对应线段成
比例。
推论的几何符号语言:
∵
DE∥BC
AD
AE
AB
AC
∴
——
——
=
(推论)
A
B
C
D
E
——
——
练习一:
1、判断题:
如图:DE∥BC,
下列各式是否正确
D:
——
——
=
AD
AE
AB
AC
(
)
C:
——
——
=
AD
AC
AE
AB
(
)
B:
——
——
=
AD
BD
AE
CE
(
)
A:
AD
AB
=
AE
AC
(
)
A
B
C
E
D
2、填空题:
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
求:
——
2
—
5
A
B
C
D
E
已知:DE//BC,
AB=15,AC=9,
BD=4
.
求:AE=?
例题
解:
∵
DE∥BC
AB
AC
BD
CE
∴
——
——
=
(推论)
15
9
4
CE
——
—
=
即
=
12
5
—
∴
CE
12
2
5
5
∴
AE=
AC+CE=9+
=11—
—
练习二:
A
B
D
C
E
EC
BC
DC
——
——
=
A
B
C
D
E
(A组)
(B组)
1、如图:
已知
DE∥BC,
AB
=
14,
AC
=
18
,
AE
=
10,
求:AD的长。
2、如图:
已知AB⊥BD,
ED⊥BD,垂足分别为
B、D。
求证:
AC
做一做
教材p53
CB
=
4,
BE
AB
=
A
A
B
C
D
E
C
达标检测题:
1、如图:
已知
DE∥BC,
AB
=
5,
AC
=
7
,
AD=
2,
求:AE的长。
B
D
E
(A组)
(B组)
2、已知
∠A
=∠E=60°
求:BD的长。
——
—
2
3
小结:
1、本节主要学行线
分线段成比例定理的推论
及它的数学符号语言;
2、本节的难点是平行线分
线段成比例定理的简单应用。
作业:
数学课本55页:
练习
1、
2题
习题23.1
7题
结束寄语
下课了!
同学们,请不要停止探究的步伐,
数学源自于对生活的热爱……
华东师大版九年数学上册
作业本里的小秘密?
A
B
C
测量线段AB和线段BC的长度,你们发现什么?
小组合作探究:
在作业本上任意画一条直线m,与相邻的三条平行线交于A、B、C三点,得到两条线段AB、BC.
m
AB=BC
n
D
E
F
DE
EF
=
所以我们
可以得到
=
=
做一做
选择作业本上不相邻的三条平行线
A
D
B
F
E
C
m
n
指出
AD、DB、FE、EC这四条线段的长度有什么关系?
我们发现:
思考:我们还可以发现哪些线段成比例?
两条直线被一组平行线所截,所得的对应线段
成比例(简称平行线分线段成比例)
F
E
C
A
D
B
几何语言:
想一想,从图中你还能得出哪些线段成比例线段?
思考1:当A点与F点重合时,就成了一个三角形的特殊情形,此时AD、DB、AE、EC这四条线段之间会有怎样的关系呢?
A
D
B
F
E
C
A
D
B
(F)
E
C
结论:
A
F
D
A
F
思考2:如图当直线m、n相交于第二条平行线上某点时,是否也有类似的成比例线段呢?
我们发现结论:
m
B
A
D
n
E
C
几何符号语言
推论:
平行于三角形一边的直线
截其他两边(或两边的延长
线),所得的对应线段成
比例。
推论的几何符号语言:
∵
DE∥BC
AD
AE
AB
AC
∴
——
——
=
(推论)
A
B
C
D
E
——
——
练习一:
1、判断题:
如图:DE∥BC,
下列各式是否正确
D:
——
——
=
AD
AE
AB
AC
(
)
C:
——
——
=
AD
AC
AE
AB
(
)
B:
——
——
=
AD
BD
AE
CE
(
)
A:
AD
AB
=
AE
AC
(
)
A
B
C
E
D
2、填空题:
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
求:
——
2
—
5
A
B
C
D
E
已知:DE//BC,
AB=15,AC=9,
BD=4
.
求:AE=?
例题
解:
∵
DE∥BC
AB
AC
BD
CE
∴
——
——
=
(推论)
15
9
4
CE
——
—
=
即
=
12
5
—
∴
CE
12
2
5
5
∴
AE=
AC+CE=9+
=11—
—
练习二:
A
B
D
C
E
EC
BC
DC
——
——
=
A
B
C
D
E
(A组)
(B组)
1、如图:
已知
DE∥BC,
AB
=
14,
AC
=
18
,
AE
=
10,
求:AD的长。
2、如图:
已知AB⊥BD,
ED⊥BD,垂足分别为
B、D。
求证:
AC
做一做
教材p53
CB
=
4,
BE
AB
=
A
A
B
C
D
E
C
达标检测题:
1、如图:
已知
DE∥BC,
AB
=
5,
AC
=
7
,
AD=
2,
求:AE的长。
B
D
E
(A组)
(B组)
2、已知
∠A
=∠E=60°
求:BD的长。
——
—
2
3
小结:
1、本节主要学行线
分线段成比例定理的推论
及它的数学符号语言;
2、本节的难点是平行线分
线段成比例定理的简单应用。
作业:
数学课本55页:
练习
1、
2题
习题23.1
7题
结束寄语
下课了!
同学们,请不要停止探究的步伐,
数学源自于对生活的热爱……
