5.3.2《圆环的面积》课件(20张PPT)
文档属性
| 名称 | 5.3.2《圆环的面积》课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 18:15:12 | ||
图片预览





文档简介
(共20张PPT)
5.3.2《圆环的面积》
C
2
=πr
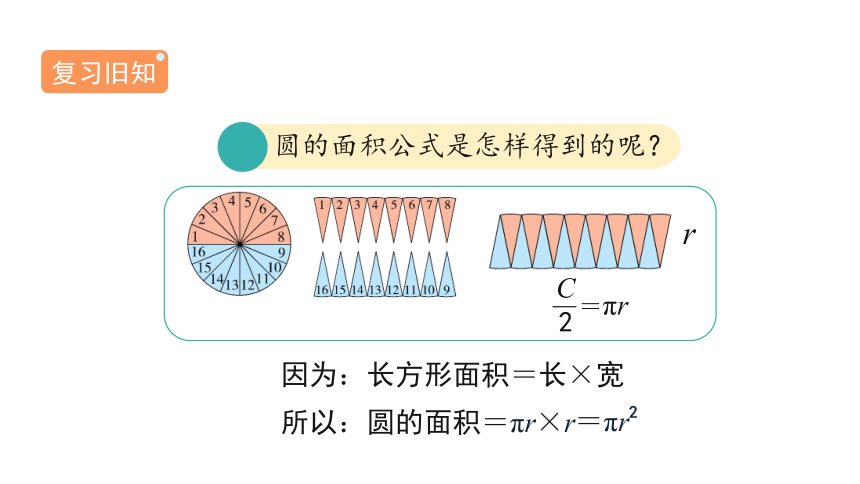
圆的面积公式是怎样得到的呢?
因为:长方形面积=长×宽
所以:圆的面积=πr×r
=πr2
r
复习旧知
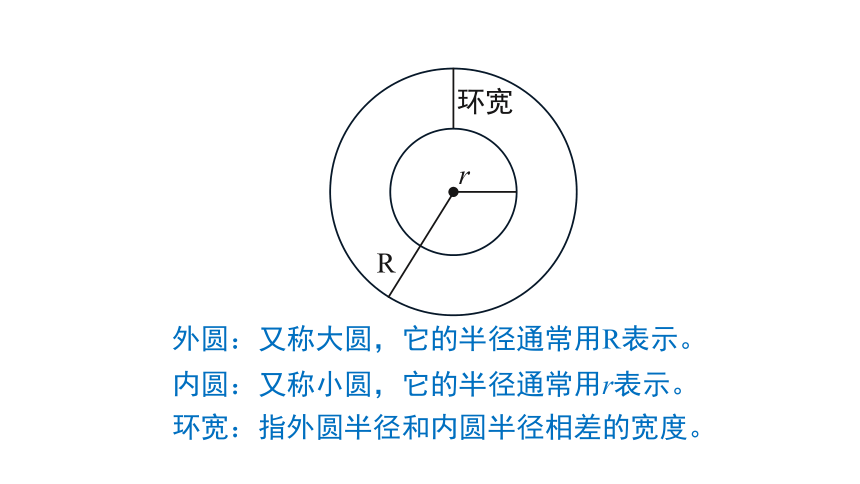
内圆:又称小圆,它的半径通常用r表示。
环宽
r
R
外圆:又称大圆,它的半径通常用R表示。
环宽:指外圆半径和内圆半径相差的宽度。
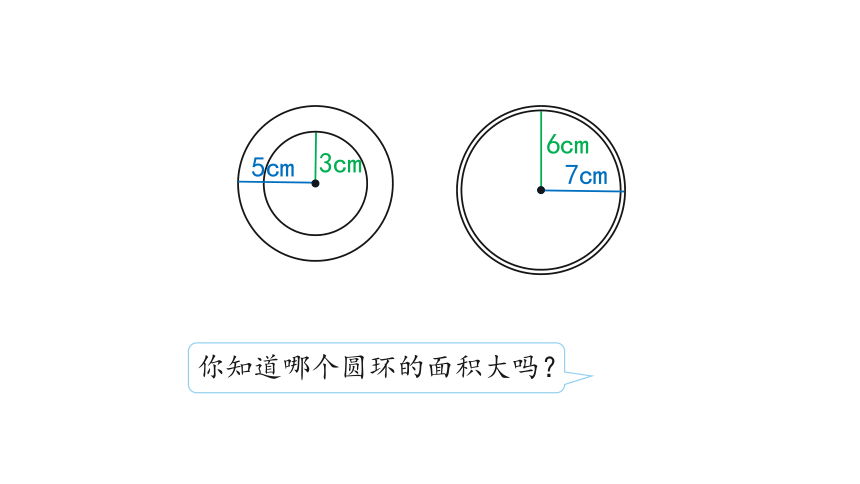
3cm
6cm
5cm
7cm
你知道哪个圆环的面积大吗?
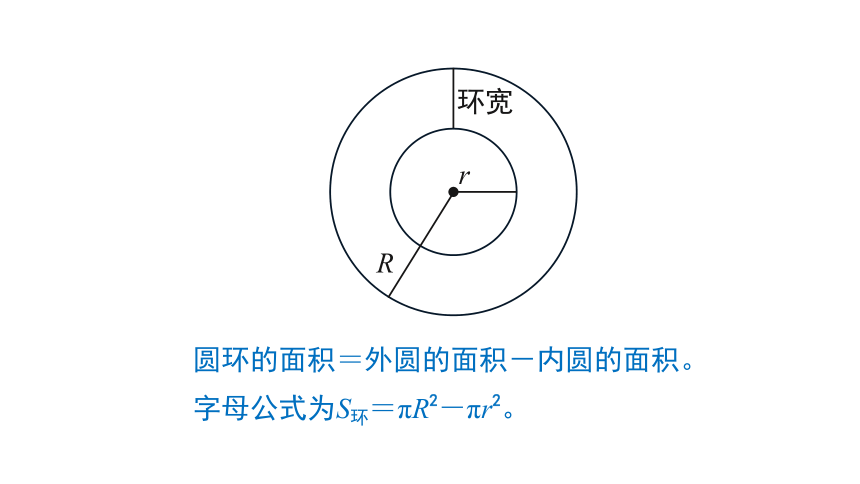
字母公式为S环=πR2-πr2。
环宽
r
R
圆环的面积=外圆的面积-内圆的面积。
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
2cm
6cm
探究新知
怎样利用内圆和外圆的面积求出圆环的面积?
3.14×62-3.14×22
答:圆环的面积是100.48cm2。
=113.04-12.56
=100.48(cm2)
=3.14×32
3.14×(62-22)
=100.48(cm2)
2.一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花
坛,其他地方是草坪。草坪的占地面积是多少?
3.14×(50÷2)2-3.14×(10÷2)2
答:草坪的占地面积是1884m2。
=3.14×252-3.14×52
=1962.5-78.5
10m
50m
=1884(m2)
巩固练习
1.下图是一块玉璧,外直径是18cm,内直径是7cm。这块玉璧的
面积是多少?
答:这块玉璧的面积是215.875cm2。
=3.14×(92-3.52)
3.14×[(18÷2)2-(7÷2)2]
=3.14×68.75
=215.875(cm2)
巩固应用
2.图中大圆的半径等于小圆的直径,请你求出阴影部分的面积。
巩固应用
答:阴影部分的面积是84.78cm2。
=3.14×36-3.14×9
3.14×62-3.14×(6÷2)2
=113.04-28.26
6cm
=84.78(cm2)
(1)一个环形铁片,外圆直径是20dm,内圆半径是7dm,这个环形铁片
的面积是多少?
(2)如图,已知阴影部分的面积是75cm ,求圆环的面积。
学习单
这节课我们学习了什么?你有哪些收获?还有什么问题?
课堂总结
填一填。
(1)如图,阴影部分是( )。外圆面积是( ) cm2,内圆面积是( )cm2,阴影部分的面积是( )cm2。
(2)在一个圆环中,外圆的半径是3 m,内圆的直径是4.8 m,环宽是( )m。
圆环
50.24
12.56
37.68
0.6
求下面各图形中阴影部分的面积。
(1) (2)
(1)3.14×(82-42)÷2=75.36(dm2)
(2)3.14×[(10÷2)2-(6÷2)2]=50.24(cm2)
如图是王师傅加工的一个环形铁片,它的外圆直径是20 cm,内圆半径是6 cm。这个铁片的面积是多少?
3.14×[(20÷2)2-62]=200.96(cm2)
答:这个铁片的面积是200.96 cm2。
有大、小两个圆(如图),大圆周长是25.12 m。小圆的面积是多少平方米?
3.14×(25.12÷3.14÷2÷2)2=12.56(m2)
答:小圆的面积是12.56 m2。
水滴滴入水中,平静的水面会产生圆形的波纹,设波纹以每秒1 m的速度向四周扩散,每隔1秒会产生一个新的波纹并且后面的波纹以相同的速度向四周扩散。请问,一滴水滴入水中4秒后的波纹比2秒后的波纹的面积大多少平方米?
3.14×(1×4)2-3.14×(1×2)2=37.68(m2)
答:一滴水滴入水中4秒后的波纹比2秒后的波纹
的面积大37.68 m2。
20÷2=10(m)
3.14×[(10+5)2-102]=392.5(m2)
答:扩建后的滑冰场面积增加了392.5 m2。
在一个周长是43.96 m的圆形花坛周围铺设2 m宽的水泥道路。这条道路的面积是多少?
43.96÷3.14÷2=7(m)
3.14×[(7+2)2-72]=100.48(m2)
答:这条道路的面积是100.48 m2。
(1)教材72页8题。
(2)找一些关于环形的资料读一读。
布置作业
5.3.2《圆环的面积》
C
2
=πr
圆的面积公式是怎样得到的呢?
因为:长方形面积=长×宽
所以:圆的面积=πr×r
=πr2
r
复习旧知
内圆:又称小圆,它的半径通常用r表示。
环宽
r
R
外圆:又称大圆,它的半径通常用R表示。
环宽:指外圆半径和内圆半径相差的宽度。
3cm
6cm
5cm
7cm
你知道哪个圆环的面积大吗?
字母公式为S环=πR2-πr2。
环宽
r
R
圆环的面积=外圆的面积-内圆的面积。
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
2cm
6cm
探究新知
怎样利用内圆和外圆的面积求出圆环的面积?
3.14×62-3.14×22
答:圆环的面积是100.48cm2。
=113.04-12.56
=100.48(cm2)
=3.14×32
3.14×(62-22)
=100.48(cm2)
2.一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花
坛,其他地方是草坪。草坪的占地面积是多少?
3.14×(50÷2)2-3.14×(10÷2)2
答:草坪的占地面积是1884m2。
=3.14×252-3.14×52
=1962.5-78.5
10m
50m
=1884(m2)
巩固练习
1.下图是一块玉璧,外直径是18cm,内直径是7cm。这块玉璧的
面积是多少?
答:这块玉璧的面积是215.875cm2。
=3.14×(92-3.52)
3.14×[(18÷2)2-(7÷2)2]
=3.14×68.75
=215.875(cm2)
巩固应用
2.图中大圆的半径等于小圆的直径,请你求出阴影部分的面积。
巩固应用
答:阴影部分的面积是84.78cm2。
=3.14×36-3.14×9
3.14×62-3.14×(6÷2)2
=113.04-28.26
6cm
=84.78(cm2)
(1)一个环形铁片,外圆直径是20dm,内圆半径是7dm,这个环形铁片
的面积是多少?
(2)如图,已知阴影部分的面积是75cm ,求圆环的面积。
学习单
这节课我们学习了什么?你有哪些收获?还有什么问题?
课堂总结
填一填。
(1)如图,阴影部分是( )。外圆面积是( ) cm2,内圆面积是( )cm2,阴影部分的面积是( )cm2。
(2)在一个圆环中,外圆的半径是3 m,内圆的直径是4.8 m,环宽是( )m。
圆环
50.24
12.56
37.68
0.6
求下面各图形中阴影部分的面积。
(1) (2)
(1)3.14×(82-42)÷2=75.36(dm2)
(2)3.14×[(10÷2)2-(6÷2)2]=50.24(cm2)
如图是王师傅加工的一个环形铁片,它的外圆直径是20 cm,内圆半径是6 cm。这个铁片的面积是多少?
3.14×[(20÷2)2-62]=200.96(cm2)
答:这个铁片的面积是200.96 cm2。
有大、小两个圆(如图),大圆周长是25.12 m。小圆的面积是多少平方米?
3.14×(25.12÷3.14÷2÷2)2=12.56(m2)
答:小圆的面积是12.56 m2。
水滴滴入水中,平静的水面会产生圆形的波纹,设波纹以每秒1 m的速度向四周扩散,每隔1秒会产生一个新的波纹并且后面的波纹以相同的速度向四周扩散。请问,一滴水滴入水中4秒后的波纹比2秒后的波纹的面积大多少平方米?
3.14×(1×4)2-3.14×(1×2)2=37.68(m2)
答:一滴水滴入水中4秒后的波纹比2秒后的波纹
的面积大37.68 m2。
20÷2=10(m)
3.14×[(10+5)2-102]=392.5(m2)
答:扩建后的滑冰场面积增加了392.5 m2。
在一个周长是43.96 m的圆形花坛周围铺设2 m宽的水泥道路。这条道路的面积是多少?
43.96÷3.14÷2=7(m)
3.14×[(7+2)2-72]=100.48(m2)
答:这条道路的面积是100.48 m2。
(1)教材72页8题。
(2)找一些关于环形的资料读一读。
布置作业
