2020-2021学年高一下学期数学人教A版必修5第二章第3节2.3 等差数列前n项和 课件(共22张PPT)
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版必修5第二章第3节2.3 等差数列前n项和 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 09:56:35 | ||
图片预览








文档简介
(共22张PPT)
2.3
等差数列的前
项和
1.等差数列的概念:
2.等差数列的通项公式:
3.等差数列的性质:
①
②
1.复习回顾
2.数列前
项和的定义
四川省叙永第一中学校
张金虎
2.3
等差数列的前
项和
3.探究发现
问题:1+2+3+
+99+100=?
5050
??
高斯(1777---1855),
德国数学家、物理学家和天文学家。他和牛顿、阿基米德,被誉为有史以来的三大数学家。有“数学王子”之称。
1
+
2
+
3
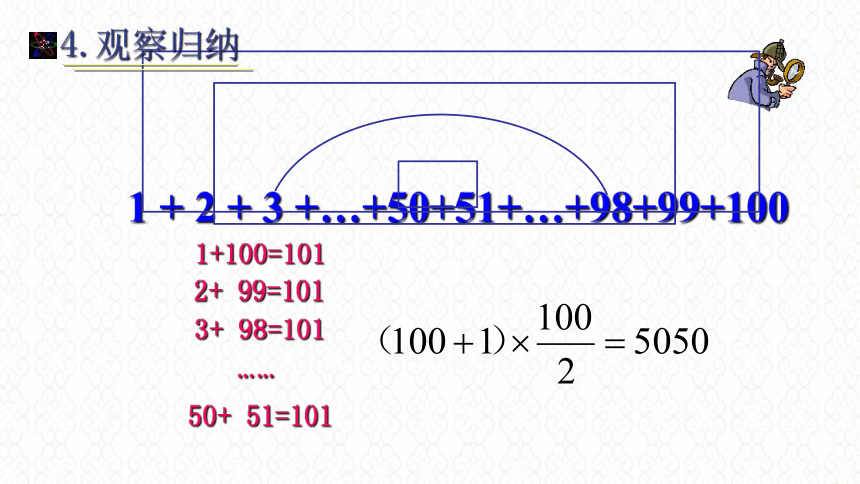
+…+50+51+…+98+99+100
1+100=101
2+
99=101
3+
98=101
……
50+
51=101
4.观察归纳
似乎与n的奇偶有关
思考:一共有多少个
5.公式推导
设等差数列{an}前n项和为Sn
,则
①
②
①+②:
倒序相加法
方程思想
共5个量,由三个公式,知三可求二
n
an
a1
a1
an
6.记忆公式
几何背景
6.记忆公式
我国数列求和的概念起源很早,在南北朝时,张丘建始创等差数列求和解法.他在《张丘建算经》中给出等差数列求和问题.例如:今有女子不善织布,每天所织的布以同数递减,初日织五尺,末一日织一尺,计织三十日,问共织几何?
原书的解法是:“并初、末日织布数,半之,再乘以织日数,即得.”
《张丘建算经》
8.例题分析
8.例题分析
方程思想
9.随堂练习
整体思想
10.走进高考
11.课堂小结
作业布置
P46
A组
2题
2.3
等差数列的前
项和
1.等差数列的概念:
2.等差数列的通项公式:
3.等差数列的性质:
①
②
1.复习回顾
2.数列前
项和的定义
四川省叙永第一中学校
张金虎
2.3
等差数列的前
项和
3.探究发现
问题:1+2+3+
+99+100=?
5050
??
高斯(1777---1855),
德国数学家、物理学家和天文学家。他和牛顿、阿基米德,被誉为有史以来的三大数学家。有“数学王子”之称。
1
+
2
+
3
+…+50+51+…+98+99+100
1+100=101
2+
99=101
3+
98=101
……
50+
51=101
4.观察归纳
似乎与n的奇偶有关
思考:一共有多少个
5.公式推导
设等差数列{an}前n项和为Sn
,则
①
②
①+②:
倒序相加法
方程思想
共5个量,由三个公式,知三可求二
n
an
a1
a1
an
6.记忆公式
几何背景
6.记忆公式
我国数列求和的概念起源很早,在南北朝时,张丘建始创等差数列求和解法.他在《张丘建算经》中给出等差数列求和问题.例如:今有女子不善织布,每天所织的布以同数递减,初日织五尺,末一日织一尺,计织三十日,问共织几何?
原书的解法是:“并初、末日织布数,半之,再乘以织日数,即得.”
《张丘建算经》
8.例题分析
8.例题分析
方程思想
9.随堂练习
整体思想
10.走进高考
11.课堂小结
作业布置
P46
A组
2题
