第十六章 分式复习学案(无答案)
文档属性
| 名称 | 第十六章 分式复习学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 50.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-13 15:12:14 | ||
图片预览



文档简介
第十六章 分式复习学案
一、复习回顾
1.分式的概念
形如 (A、B是整式,且B中含有字母(未知数),B≠0)的式子,叫做分式。其中A叫做分式的分子,B叫做分式的分母。 和 统称有理式。
注意:在分式中,分母的值不能是零.如果分母的值是零,则分式没有意义。(分式有意义的条件)
(二)分式的基本性质
1.分式的基本性质:
2.分式的变号法则:
(三)分式的运算
1、分式的乘法
分式的乘法法则:
用式子表示为: .
进行分式的乘法运算时应注意:
2、分式的除法
分式的除法法则:
用式子表示为: .
3、分式的乘方
分式的乘方法则:
用式子表示为: ,
⑴分式乘方时,一定要把分式加上括号.如:;
⑵分式乘方时,分式本身的符号也要同时乘方;
4、同分母的分式加减法
用式子表示为:.
5、异分母的分式加减法
6、分式的混合运算
分式混合运算的顺序为: 运算过程中,要灵活运用交换律、结合律、分配律等,运算结果必须是最简分式或整式.
二、复习巩固
1.填空题(1)当x 时,分式有意义; (2)当x 时,分式有意义;
(3)当b 时,分式 有意义; (4)当x、y 满足关系 时,分式 有意义。
(5)若分式有意义,则x ; (6)若分式无意义,则x= 。
(7)若分式有意义,则a__________. (8) 若分式有意义,则x___________.
(9)当x为 时,分式的值为正数;(10)当x为 时,分式的值为负数;
(11)
= = =
(12) 把下列各数用科学记数法表示:100000= 0.0000000012=
-11200000= -0.00000034=
(13) 直接写出化简结果:
1) ;2) ;3)
4) ;5) ;6)
(14)若关于x的方程的解是x=1,则m= ;
(15)若方程有增根,则;
(16)如果分式方程无解,则m= ;
三.解答题
(1) (2)
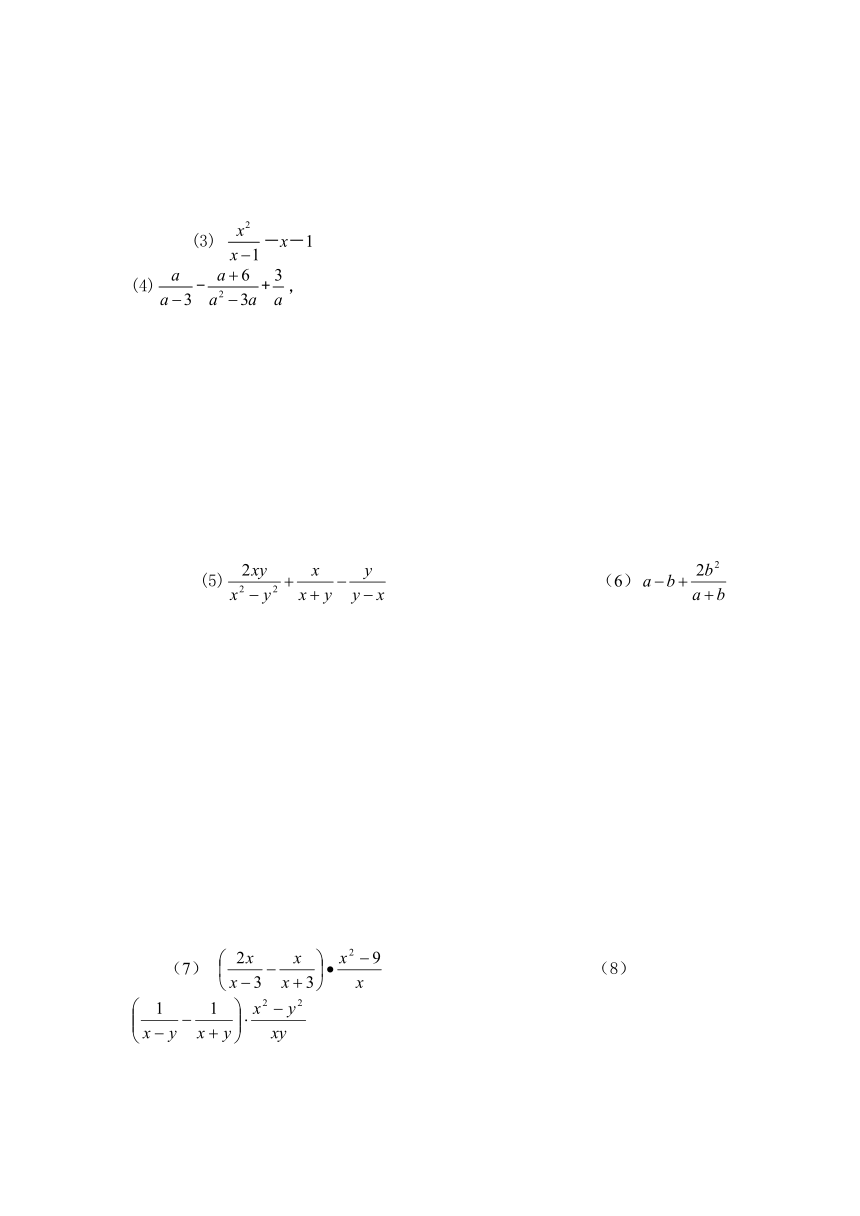
(3) -x-1 (4)-+,
(5) (6)
(7) (8)
(9). ⑽
(11) (12)
(13) (14)
(15)计算(结果用科学记数法表示)
(1) (2)
16. 计算,并求出当-1的值.
17.计算:,并求当时原式的值.
18.先化简,再取一个你喜欢的数代入求值:
19.请你先将式子化简,然后从-1,0,1,2中选择一个适当数作为的值代入其中求值.
20.先化简,再求值:,其中x=-3 。
四.解方程: (1) (2)
(3)=-2 (4)
(5) (6)
五、列方程解应用题
1. 学校要举行跳绳比赛,同学们都积极练习.甲同学跳180个所用的时间,乙同学可以跳240个;又已知甲每分钟比乙少跳5个,求每人每分钟各跳多少个.
2. 每年3月12日为“植树节”,某中学积极响应“植树造林”活动的号召,组织团员植树300棵。实际参加植树的团员人数是原计划的1.5倍,这样实际人均植树棵数比原计划的少2棵,求原计划参加植树的团员有多少人?
3. 甲、乙两地相距19千米,某人从甲地去乙地,先步行7千米,然后改骑自行车,共用了2小时到达乙地,已知这个人骑自行车的速度是步行速度的4倍,求步行的速度和骑自行车的速度.
4 .甲做180个机器零件与乙做240个机器零件所用的时间相同,已知两人每小时共做70个机器零件,两人每小时各做多少个?
一、复习回顾
1.分式的概念
形如 (A、B是整式,且B中含有字母(未知数),B≠0)的式子,叫做分式。其中A叫做分式的分子,B叫做分式的分母。 和 统称有理式。
注意:在分式中,分母的值不能是零.如果分母的值是零,则分式没有意义。(分式有意义的条件)
(二)分式的基本性质
1.分式的基本性质:
2.分式的变号法则:
(三)分式的运算
1、分式的乘法
分式的乘法法则:
用式子表示为: .
进行分式的乘法运算时应注意:
2、分式的除法
分式的除法法则:
用式子表示为: .
3、分式的乘方
分式的乘方法则:
用式子表示为: ,
⑴分式乘方时,一定要把分式加上括号.如:;
⑵分式乘方时,分式本身的符号也要同时乘方;
4、同分母的分式加减法
用式子表示为:.
5、异分母的分式加减法
6、分式的混合运算
分式混合运算的顺序为: 运算过程中,要灵活运用交换律、结合律、分配律等,运算结果必须是最简分式或整式.
二、复习巩固
1.填空题(1)当x 时,分式有意义; (2)当x 时,分式有意义;
(3)当b 时,分式 有意义; (4)当x、y 满足关系 时,分式 有意义。
(5)若分式有意义,则x ; (6)若分式无意义,则x= 。
(7)若分式有意义,则a__________. (8) 若分式有意义,则x___________.
(9)当x为 时,分式的值为正数;(10)当x为 时,分式的值为负数;
(11)
= = =
(12) 把下列各数用科学记数法表示:100000= 0.0000000012=
-11200000= -0.00000034=
(13) 直接写出化简结果:
1) ;2) ;3)
4) ;5) ;6)
(14)若关于x的方程的解是x=1,则m= ;
(15)若方程有增根,则;
(16)如果分式方程无解,则m= ;
三.解答题
(1) (2)
(3) -x-1 (4)-+,
(5) (6)
(7) (8)
(9). ⑽
(11) (12)
(13) (14)
(15)计算(结果用科学记数法表示)
(1) (2)
16. 计算,并求出当-1的值.
17.计算:,并求当时原式的值.
18.先化简,再取一个你喜欢的数代入求值:
19.请你先将式子化简,然后从-1,0,1,2中选择一个适当数作为的值代入其中求值.
20.先化简,再求值:,其中x=-3 。
四.解方程: (1) (2)
(3)=-2 (4)
(5) (6)
五、列方程解应用题
1. 学校要举行跳绳比赛,同学们都积极练习.甲同学跳180个所用的时间,乙同学可以跳240个;又已知甲每分钟比乙少跳5个,求每人每分钟各跳多少个.
2. 每年3月12日为“植树节”,某中学积极响应“植树造林”活动的号召,组织团员植树300棵。实际参加植树的团员人数是原计划的1.5倍,这样实际人均植树棵数比原计划的少2棵,求原计划参加植树的团员有多少人?
3. 甲、乙两地相距19千米,某人从甲地去乙地,先步行7千米,然后改骑自行车,共用了2小时到达乙地,已知这个人骑自行车的速度是步行速度的4倍,求步行的速度和骑自行车的速度.
4 .甲做180个机器零件与乙做240个机器零件所用的时间相同,已知两人每小时共做70个机器零件,两人每小时各做多少个?
