华师大版数学九年级上册23.3.3相似三角形的性质 课件(共25张PPT)
文档属性
| 名称 | 华师大版数学九年级上册23.3.3相似三角形的性质 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 15:14:14 | ||
图片预览



文档简介
(共25张PPT)
第23章
23.3.3相似三角形的性质
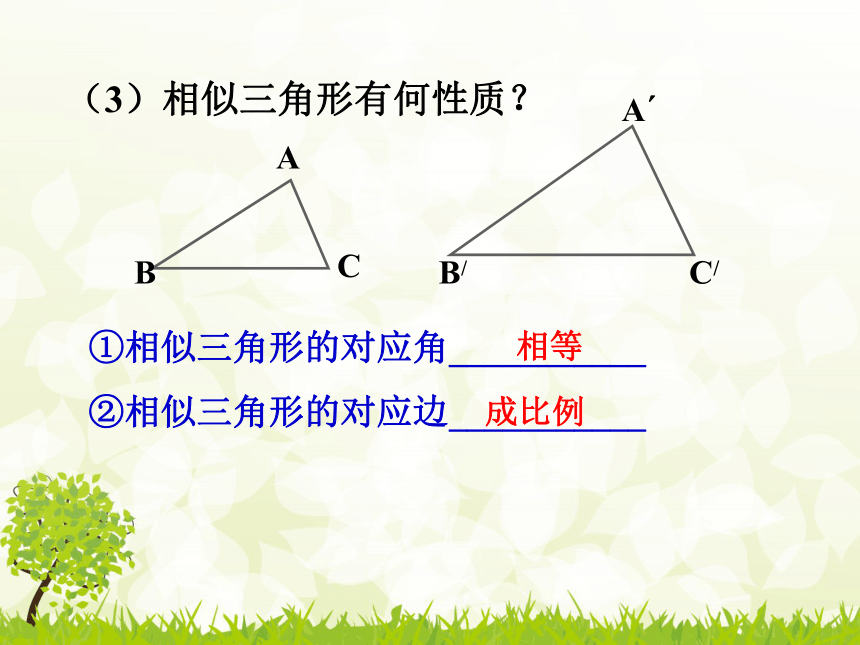
(1)什么叫相似三角形?
对应边成比例、对应角相等的三角形叫做相似三角形.
(2)如何判定两个三角形相似?
①平行得相似;
复习回顾
②两个角对应相等;
③两边对应成比例及其夹角相等;
④三边对应成比例.
A
B
C
A?
B/
C/
①相似三角形的对应角___________
②相似三角形的对应边___________
(3)相似三角形有何性质?
相等
成比例
一个三角形除了三条边和三个角,它还有周长、面积以及三类重要线段:
如果两个三角形相似,那么这些量与三角形相似比有什么关系呢?
情境引入
高、中线、角平分线
新课导入
A
C
B
A′
B′
C′
(1)
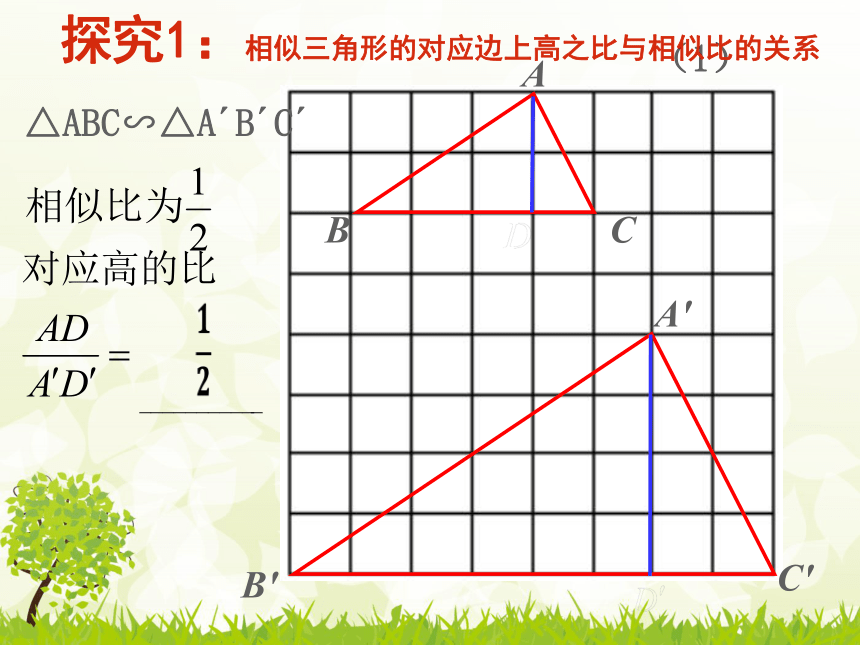
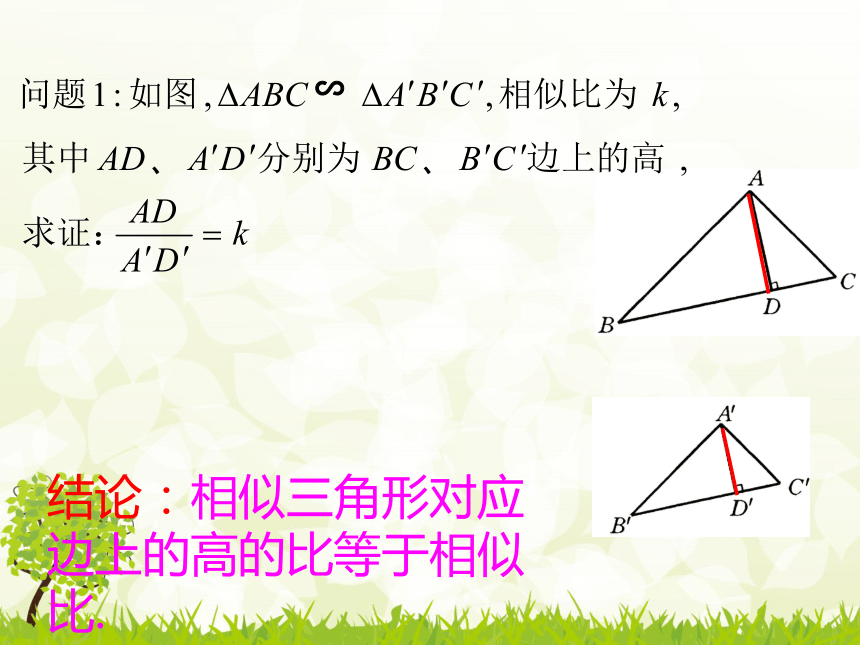
探究1:相似三角形的对应边上高之比与相似比的关系
△ABC∽△A?B?C?
∽
结论:相似三角形对应边上的高的比等于相似比.
A
C
B
A′
B′
C′
填一填
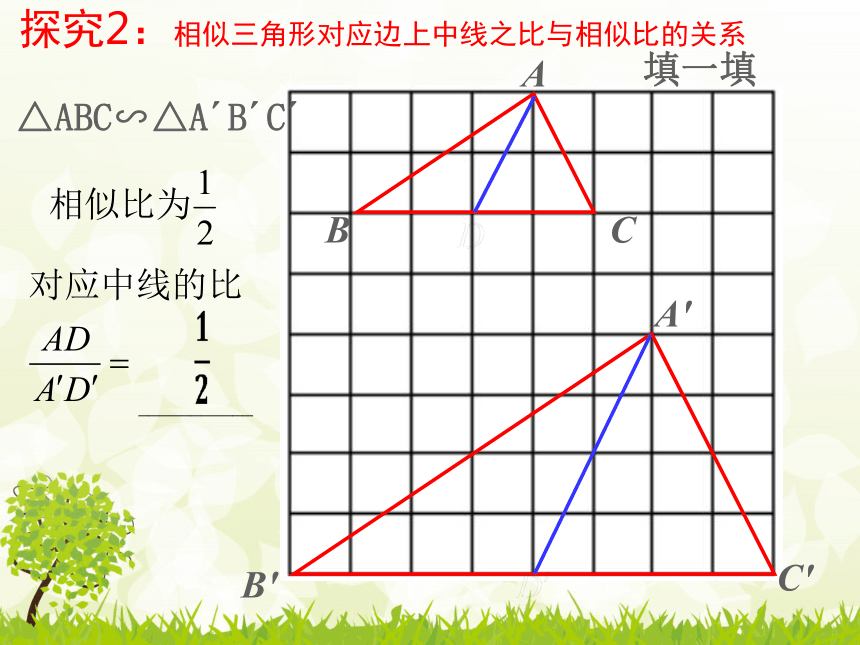
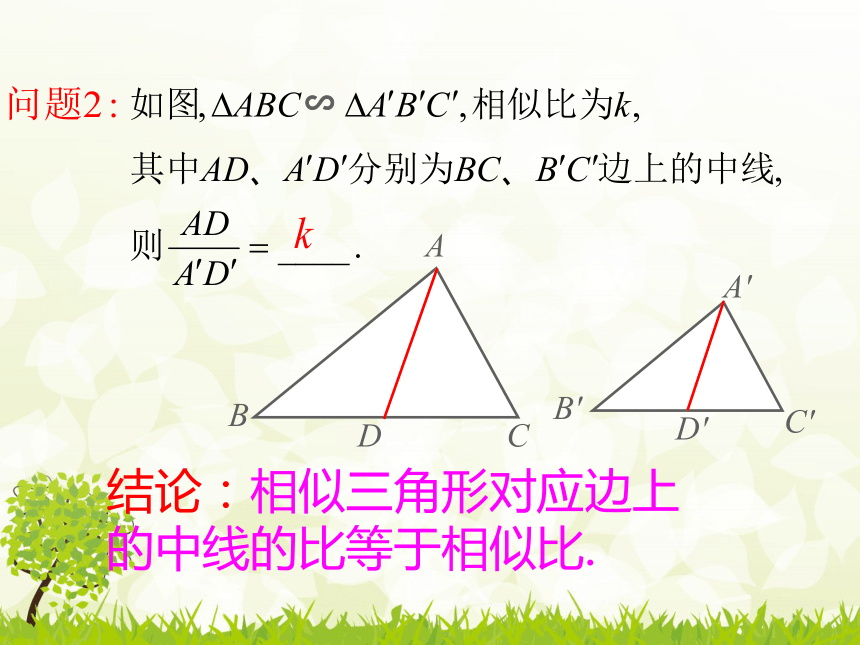
探究2:相似三角形对应边上中线之比与相似比的关系
△ABC∽△A?B?C?
D'
C'
B'
A'
D
C
B
A
∽
结论:相似三角形对应边上的中线的比等于相似比.
A′
C′
B′
C
B
A
E′
E
∽
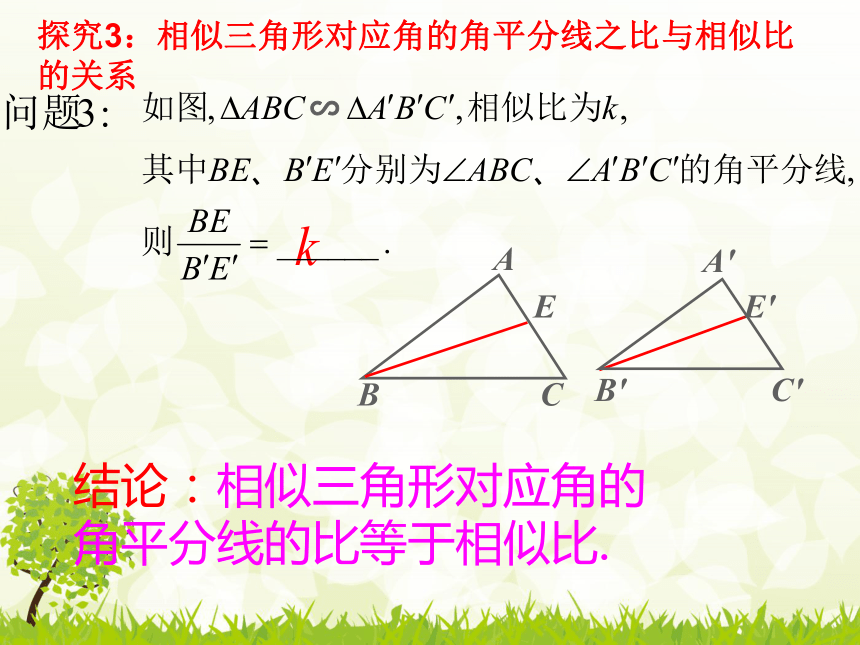
结论:相似三角形对应角的角平分线的比等于相似比.
探究3:相似三角形对应角的角平分线之比与相似比的关系
问题4:两个相似三角形的周长比会等于相似比吗?
已知△ABC∽△
,且相似比为k。
求证:△ABC、
周长的比等于k
证明:
△ABC∽
即△ABC、△
的周长比等于相似比
∵
∴
∴
结论:相似三角形的周长比等于相似比.
△
问题5:两个相似三角形的面积比与
相似比之间有什么关系呢?
探究4
1
2
3
1∶
2
当相似比=k时,面积比等于什么?
(1)
(2)
(3)
(1)与(2)的相似比=______
(1)与(2)的面积比=______
(2)与(3)的相似比=______
(2)与(3)的面积比=______
1∶
4
2∶3
4∶
9
猜想:相似三角形面积的比等于相似比的平方.
已知△ABC∽△A?B?C?,且相似比为k,AD、A?D?分别是△ABC、△
A?B?C?
对应边BC、B?C?上的高,求证:
证明:
∵△ABC∽△
A?B?C?
∴
∴
结论:相似三角形面积的比等于相似比的平方.
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
小结:本节课你有哪些收获?
比例
相等
相似比
相似比
基础训练:(小试牛刀)
1、若两个三角形相似比为3:4,那么对应高的比为______,对应中线的比为______,对应角平分线的比为_______.
2、若两个相似三角形的周长比为3:5,则这两个三角形的相似比为______,
对应高之比为_____,面积之比为____
3、若两个相似三角形的最大边长分别为6cm和8cm,它们的周长和为35cm,则较小三角形的周长为______,它们对应边上高之比为_______
4.两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长是
cm,面积
cm2。
3:4
3:4
3:4
3:5
3:5
6:25
15cm
3:4
14
5、如图在△ABC中,D是AB边上一点,E是AC边上一点,且DE‖BC,F是BC边上一点,AF与DE相交于点G,若AD:DB=2:1,BC=3则DE的长为______,AG:AF=______
S△ABC:S△ADE=_____
A
C
E
B
F
D
G
2
2:3
9:4
(1)△ADE与△ABC相似吗?如果相似,
求它们的相似比.
A
B
C
D
E
1∶4
(2)
△ADE的周长︰△ABC的周长=_______.
1∶4
6
、如图,DE∥BC,
DE
=
1,
BC
=
4,
(4)
7、如图,在
ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5cm2,
则?CDF的面积为______.
B
F
E
D
C
A
1
:
2
20
cm2
∵?AEF与?CDF
能力挑战:
例1、如图,在梯形ABCD中,AD//BC,且AD:BC=2:5,对角线AC、BD相交于点O,则
A
D
O
B
C
例2:如图,△ABC中,BC=24㎝,高AD=12㎝,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H在AC、AB上,且EF:EH=4:3,求EF、EH的长
A
B
C
H
E
F
G
K
D
∟
一、相似三角形的基本性质:
对应边成比例,对应角相等
二、相似三角形的性质:
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
小结:
小王有一块三角形余料ABC,它的边BC=60cm,高线AD=40cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上
挑战自我
A
B
C
S
R
E
P
D
Q
(1)△
ASR与△
ABC相似吗?为什么?
(2)求正方形SPQR的面积。
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的面积.
分析:(1)
△ASR∽△ABC.理由是:
(2)由(1)可知,
△ASR∽△ABC.
四边形PQRS是正方形
RS∥BC
∠ASR=
∠B
∠ARS=
∠C
△ASR∽△ABC.
设正方形PQRS的边长为x
cm,
则AE=(40-x)cm,
解得x=24.
所以正方形PQRS的面积为576cm2.
(相似三角形对应高的比等于相似比)
例
题
解
析
A
B
C
S
R
E
P
D
Q
40
60
3.如图,在
ABCD中,E为AB延长线上一点,AB:AE=2:5,若S△DFC=12cm2,求S△EFB
D
A
B
C
E
F
第23章
23.3.3相似三角形的性质
(1)什么叫相似三角形?
对应边成比例、对应角相等的三角形叫做相似三角形.
(2)如何判定两个三角形相似?
①平行得相似;
复习回顾
②两个角对应相等;
③两边对应成比例及其夹角相等;
④三边对应成比例.
A
B
C
A?
B/
C/
①相似三角形的对应角___________
②相似三角形的对应边___________
(3)相似三角形有何性质?
相等
成比例
一个三角形除了三条边和三个角,它还有周长、面积以及三类重要线段:
如果两个三角形相似,那么这些量与三角形相似比有什么关系呢?
情境引入
高、中线、角平分线
新课导入
A
C
B
A′
B′
C′
(1)
探究1:相似三角形的对应边上高之比与相似比的关系
△ABC∽△A?B?C?
∽
结论:相似三角形对应边上的高的比等于相似比.
A
C
B
A′
B′
C′
填一填
探究2:相似三角形对应边上中线之比与相似比的关系
△ABC∽△A?B?C?
D'
C'
B'
A'
D
C
B
A
∽
结论:相似三角形对应边上的中线的比等于相似比.
A′
C′
B′
C
B
A
E′
E
∽
结论:相似三角形对应角的角平分线的比等于相似比.
探究3:相似三角形对应角的角平分线之比与相似比的关系
问题4:两个相似三角形的周长比会等于相似比吗?
已知△ABC∽△
,且相似比为k。
求证:△ABC、
周长的比等于k
证明:
△ABC∽
即△ABC、△
的周长比等于相似比
∵
∴
∴
结论:相似三角形的周长比等于相似比.
△
问题5:两个相似三角形的面积比与
相似比之间有什么关系呢?
探究4
1
2
3
1∶
2
当相似比=k时,面积比等于什么?
(1)
(2)
(3)
(1)与(2)的相似比=______
(1)与(2)的面积比=______
(2)与(3)的相似比=______
(2)与(3)的面积比=______
1∶
4
2∶3
4∶
9
猜想:相似三角形面积的比等于相似比的平方.
已知△ABC∽△A?B?C?,且相似比为k,AD、A?D?分别是△ABC、△
A?B?C?
对应边BC、B?C?上的高,求证:
证明:
∵△ABC∽△
A?B?C?
∴
∴
结论:相似三角形面积的比等于相似比的平方.
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
小结:本节课你有哪些收获?
比例
相等
相似比
相似比
基础训练:(小试牛刀)
1、若两个三角形相似比为3:4,那么对应高的比为______,对应中线的比为______,对应角平分线的比为_______.
2、若两个相似三角形的周长比为3:5,则这两个三角形的相似比为______,
对应高之比为_____,面积之比为____
3、若两个相似三角形的最大边长分别为6cm和8cm,它们的周长和为35cm,则较小三角形的周长为______,它们对应边上高之比为_______
4.两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长是
cm,面积
cm2。
3:4
3:4
3:4
3:5
3:5
6:25
15cm
3:4
14
5、如图在△ABC中,D是AB边上一点,E是AC边上一点,且DE‖BC,F是BC边上一点,AF与DE相交于点G,若AD:DB=2:1,BC=3则DE的长为______,AG:AF=______
S△ABC:S△ADE=_____
A
C
E
B
F
D
G
2
2:3
9:4
(1)△ADE与△ABC相似吗?如果相似,
求它们的相似比.
A
B
C
D
E
1∶4
(2)
△ADE的周长︰△ABC的周长=_______.
1∶4
6
、如图,DE∥BC,
DE
=
1,
BC
=
4,
(4)
7、如图,在
ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5cm2,
则?CDF的面积为______.
B
F
E
D
C
A
1
:
2
20
cm2
∵?AEF与?CDF
能力挑战:
例1、如图,在梯形ABCD中,AD//BC,且AD:BC=2:5,对角线AC、BD相交于点O,则
A
D
O
B
C
例2:如图,△ABC中,BC=24㎝,高AD=12㎝,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H在AC、AB上,且EF:EH=4:3,求EF、EH的长
A
B
C
H
E
F
G
K
D
∟
一、相似三角形的基本性质:
对应边成比例,对应角相等
二、相似三角形的性质:
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
小结:
小王有一块三角形余料ABC,它的边BC=60cm,高线AD=40cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上
挑战自我
A
B
C
S
R
E
P
D
Q
(1)△
ASR与△
ABC相似吗?为什么?
(2)求正方形SPQR的面积。
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的面积.
分析:(1)
△ASR∽△ABC.理由是:
(2)由(1)可知,
△ASR∽△ABC.
四边形PQRS是正方形
RS∥BC
∠ASR=
∠B
∠ARS=
∠C
△ASR∽△ABC.
设正方形PQRS的边长为x
cm,
则AE=(40-x)cm,
解得x=24.
所以正方形PQRS的面积为576cm2.
(相似三角形对应高的比等于相似比)
例
题
解
析
A
B
C
S
R
E
P
D
Q
40
60
3.如图,在
ABCD中,E为AB延长线上一点,AB:AE=2:5,若S△DFC=12cm2,求S△EFB
D
A
B
C
E
F
