2.4 曲线与方程 同步课时作业——2021-2022学年高二上学期数学人教B版(2019)选择性必修第一册(Word含答案解析)
文档属性
| 名称 | 2.4 曲线与方程 同步课时作业——2021-2022学年高二上学期数学人教B版(2019)选择性必修第一册(Word含答案解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 00:00:00 | ||
图片预览


文档简介
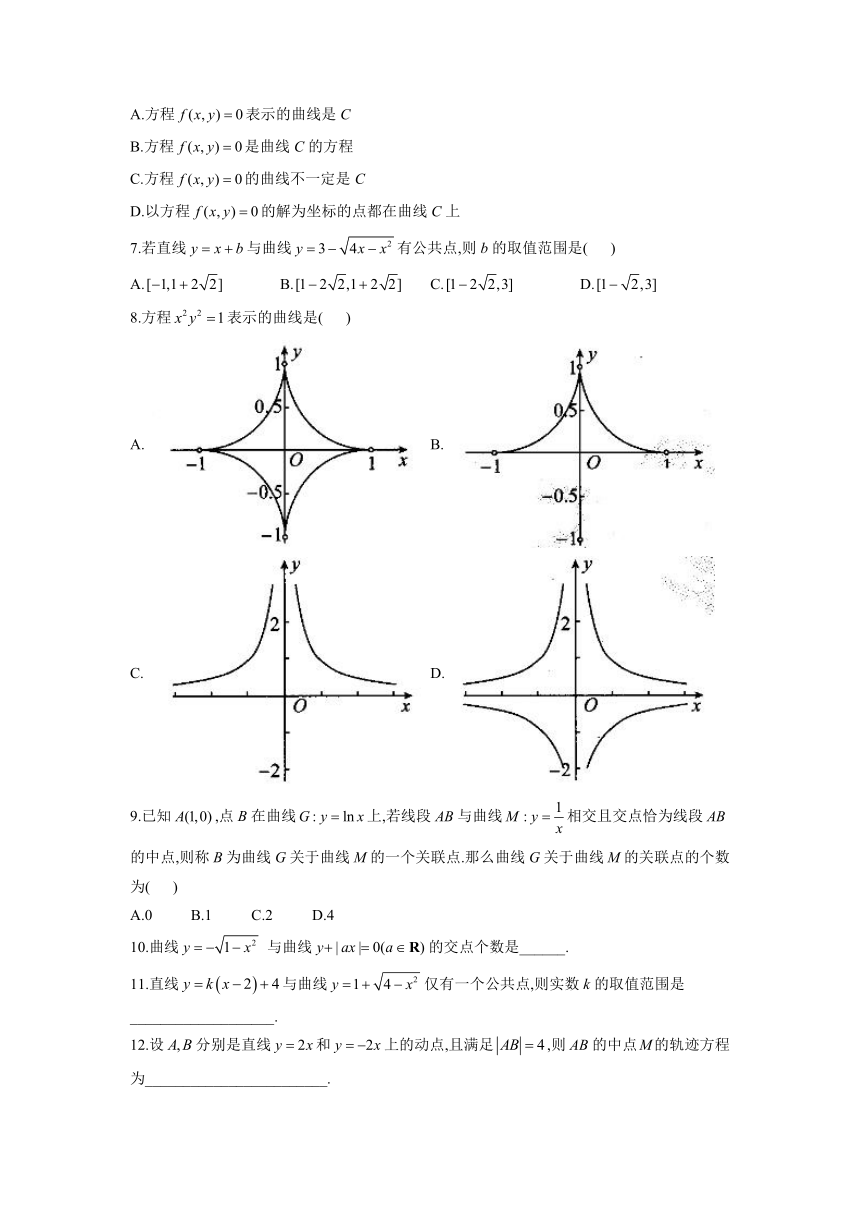
2.4
曲线与方程-2021-2022学年高二数学人教B版(2019)选择性必修第一册同步课时作业
1.直线与曲线有且仅有一个公共点,则b的取值范围是(
)
A.
B.或
C.
D.以上都不对
2.若方程与所表示的两条直线的交点在方程所表示的曲线上,则实数k的值为(
)
A.0
B.
C.
D.一切实数
3.已知在平面直角坐标系中,动点到两坐标轴的距离之和等于它到点的距离,记点P的轨迹为曲线W,则有下列命题:
①曲线W关于原点对称;
②曲线W关于x轴对称;
③曲线W关于y轴对称;
④曲线W关于直线对称.
其中真命题的个数是(
)
A.1
B.2
C.3
D.4
4.方程表示的曲线是下图中的(
)
A.
B.
C.
D.
5.在平面直角坐标系内到两坐标轴距离之差等于1的动点的轨迹方程是(
)
A.
B.
C.
D.
6.若命题“曲线C上的点的坐标都是方程的解”是真命题,则下列命题中是真命题的为(
)
A.方程表示的曲线是C
B.方程是曲线C的方程
C.方程的曲线不一定是C
D.以方程的解为坐标的点都在曲线C上
7.若直线与曲线有公共点,则b的取值范围是(
)
A.
B.
C.
D.
8.方程表示的曲线是(
)
A.
B.
C.
D.
9.已知,点B在曲线上,若线段与曲线相交且交点恰为线段的中点,则称B为曲线G关于曲线M的一个关联点.那么曲线G关于曲线M的关联点的个数为(
)
A.0
B.1
C.2
D.4
10.曲线与曲线的交点个数是______.
11.直线与曲线仅有一个公共点,则实数k的取值范围是___________________.
12.设分别是直线和上的动点,且满足,则的中点M的轨迹方程为________________________.
13.定义在区间
上的函数的图象与的图象的交点个数是__________.
14.已知动点M到点的距离是它到点的距离的一半.
(1)求动点M的轨迹方程;
(2)若N是线段AM的中点,试求点N的轨迹.
答案以及解析
1.答案:B
解析:由得,,该曲线表示的是圆在y轴及右侧的部分,如图所示,表示斜率为1,在y轴上的截距为b的直线.由直线与圆相切,得圆心到直线的距离,结合图形知b的取值范围是,或.故选B.
2.答案:C
解析:两直线的交点为,又点在曲线上,所以,解得.故选C.
3.答案:A
解析:由题意,可知,从方程可以看出,当x换成或y换成或两者同时替换时,方程改变,只有当x,y互换时,方程不变,因此曲线W关于直线对称.只有④是真命题.故选A.
4.答案:C
解析:当时,,当时,,所以.故选C.
5.答案:C
解析:动点到x,y轴的距离分别为,,由题意,得,即,故选C.
6.答案:C
解析:根据曲线与方程的关系可知A,B,D错误.
7.答案:C
解析:如图所示,曲线即,表示以为圆心,以2为半径的一个半圆,由圆心到直线的距离等于半径2,可得,所以.当直线过点时,直线与曲线有两个公共点,此时.结合图像可得.故选C.
8.答案:D
解析:由题意,方程可化为或,即或,根据反比例函数的图像与性质,即可得选项D中的图像为方程表示的曲线.故选D.
9.答案:B
解析:设,线段的中点为C,则.又点C在曲线M上,所以,即.此方程的解的个数可以看作函数与的图像的交点的个数.画出图象,如图所示,可知函数与的图象只有1个交点.故选B.
10.答案:2
解析:即.对于,当时,,当时,
.画出它们在同一平面直角坐标系中的大致图像如图所示,
由图知曲线与曲线的交点个数为2.
11.答案:
解析:如图,曲线,即,表示以为圆心,2为半径的半圆,该半圆位于直线上方.直线恒过点,
由圆心到直线的距离等于半径得,解得.
由图可知,当直线经过点时,直线的斜率为,
当直线经过点时,直线的斜率不存在.
综上,实数k的取值范围是.
12.答案:
解析:设,
则的中点,所以.
又,
即,
所以的中点M的轨迹方程为.
13.答案:7
解析:由
或,因为,
所以共个.
14.答案:(1)设动点为轨迹上任意一点,由,得,
整理得.
故动点M的轨迹方程为.
(2)设动点,点,
是线段AM的中点,
由中点坐标公式,得,即,
,,
即,
点N的轨迹是以为圆心,2为半径的圆.
曲线与方程-2021-2022学年高二数学人教B版(2019)选择性必修第一册同步课时作业
1.直线与曲线有且仅有一个公共点,则b的取值范围是(
)
A.
B.或
C.
D.以上都不对
2.若方程与所表示的两条直线的交点在方程所表示的曲线上,则实数k的值为(
)
A.0
B.
C.
D.一切实数
3.已知在平面直角坐标系中,动点到两坐标轴的距离之和等于它到点的距离,记点P的轨迹为曲线W,则有下列命题:
①曲线W关于原点对称;
②曲线W关于x轴对称;
③曲线W关于y轴对称;
④曲线W关于直线对称.
其中真命题的个数是(
)
A.1
B.2
C.3
D.4
4.方程表示的曲线是下图中的(
)
A.
B.
C.
D.
5.在平面直角坐标系内到两坐标轴距离之差等于1的动点的轨迹方程是(
)
A.
B.
C.
D.
6.若命题“曲线C上的点的坐标都是方程的解”是真命题,则下列命题中是真命题的为(
)
A.方程表示的曲线是C
B.方程是曲线C的方程
C.方程的曲线不一定是C
D.以方程的解为坐标的点都在曲线C上
7.若直线与曲线有公共点,则b的取值范围是(
)
A.
B.
C.
D.
8.方程表示的曲线是(
)
A.
B.
C.
D.
9.已知,点B在曲线上,若线段与曲线相交且交点恰为线段的中点,则称B为曲线G关于曲线M的一个关联点.那么曲线G关于曲线M的关联点的个数为(
)
A.0
B.1
C.2
D.4
10.曲线与曲线的交点个数是______.
11.直线与曲线仅有一个公共点,则实数k的取值范围是___________________.
12.设分别是直线和上的动点,且满足,则的中点M的轨迹方程为________________________.
13.定义在区间
上的函数的图象与的图象的交点个数是__________.
14.已知动点M到点的距离是它到点的距离的一半.
(1)求动点M的轨迹方程;
(2)若N是线段AM的中点,试求点N的轨迹.
答案以及解析
1.答案:B
解析:由得,,该曲线表示的是圆在y轴及右侧的部分,如图所示,表示斜率为1,在y轴上的截距为b的直线.由直线与圆相切,得圆心到直线的距离,结合图形知b的取值范围是,或.故选B.
2.答案:C
解析:两直线的交点为,又点在曲线上,所以,解得.故选C.
3.答案:A
解析:由题意,可知,从方程可以看出,当x换成或y换成或两者同时替换时,方程改变,只有当x,y互换时,方程不变,因此曲线W关于直线对称.只有④是真命题.故选A.
4.答案:C
解析:当时,,当时,,所以.故选C.
5.答案:C
解析:动点到x,y轴的距离分别为,,由题意,得,即,故选C.
6.答案:C
解析:根据曲线与方程的关系可知A,B,D错误.
7.答案:C
解析:如图所示,曲线即,表示以为圆心,以2为半径的一个半圆,由圆心到直线的距离等于半径2,可得,所以.当直线过点时,直线与曲线有两个公共点,此时.结合图像可得.故选C.
8.答案:D
解析:由题意,方程可化为或,即或,根据反比例函数的图像与性质,即可得选项D中的图像为方程表示的曲线.故选D.
9.答案:B
解析:设,线段的中点为C,则.又点C在曲线M上,所以,即.此方程的解的个数可以看作函数与的图像的交点的个数.画出图象,如图所示,可知函数与的图象只有1个交点.故选B.
10.答案:2
解析:即.对于,当时,,当时,
.画出它们在同一平面直角坐标系中的大致图像如图所示,
由图知曲线与曲线的交点个数为2.
11.答案:
解析:如图,曲线,即,表示以为圆心,2为半径的半圆,该半圆位于直线上方.直线恒过点,
由圆心到直线的距离等于半径得,解得.
由图可知,当直线经过点时,直线的斜率为,
当直线经过点时,直线的斜率不存在.
综上,实数k的取值范围是.
12.答案:
解析:设,
则的中点,所以.
又,
即,
所以的中点M的轨迹方程为.
13.答案:7
解析:由
或,因为,
所以共个.
14.答案:(1)设动点为轨迹上任意一点,由,得,
整理得.
故动点M的轨迹方程为.
(2)设动点,点,
是线段AM的中点,
由中点坐标公式,得,即,
,,
即,
点N的轨迹是以为圆心,2为半径的圆.
