山东省潍坊市安丘市2020-2021学年八年级下学期期末数学试卷(word解析版)
文档属性
| 名称 | 山东省潍坊市安丘市2020-2021学年八年级下学期期末数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 447.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 21:34:39 | ||
图片预览


文档简介
2020-2021学年山东省潍坊市安丘市八年级(下)期末数学试卷
一、单项选择题(每小题3分,共24分.每小题给出的四个选项中只有一项是正确的)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
A.赵爽弦图
B.笛卡尔心形线
C.科克曲线
D.斐波那契螺旋线
2.的相反数是( )
A.﹣3
B.3
C.
D.﹣9
3.下列属于最简二次根式的是( )
A.
B.
C.
D.
4.一根1m长的木杆,竖直放置在地面上,影长为1.5m,同一时刻,一棵树落在地面上的影长为12m,则树高为( )
A.6m
B.8m
C.12m
D.18m
5.一次函数y=mx﹣m(m为常数且m≠0),若y随x增大而增大,则它的图象经过( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
6.如图,函数y=3x和y=ax+4的图象相交于点A(m,3),则不等式3x≤ax+4的解集为( )
A.x≥1
B.x≤1
C.x≤3
D.x≥3
7.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A.
B.
C.﹣1
D.﹣1
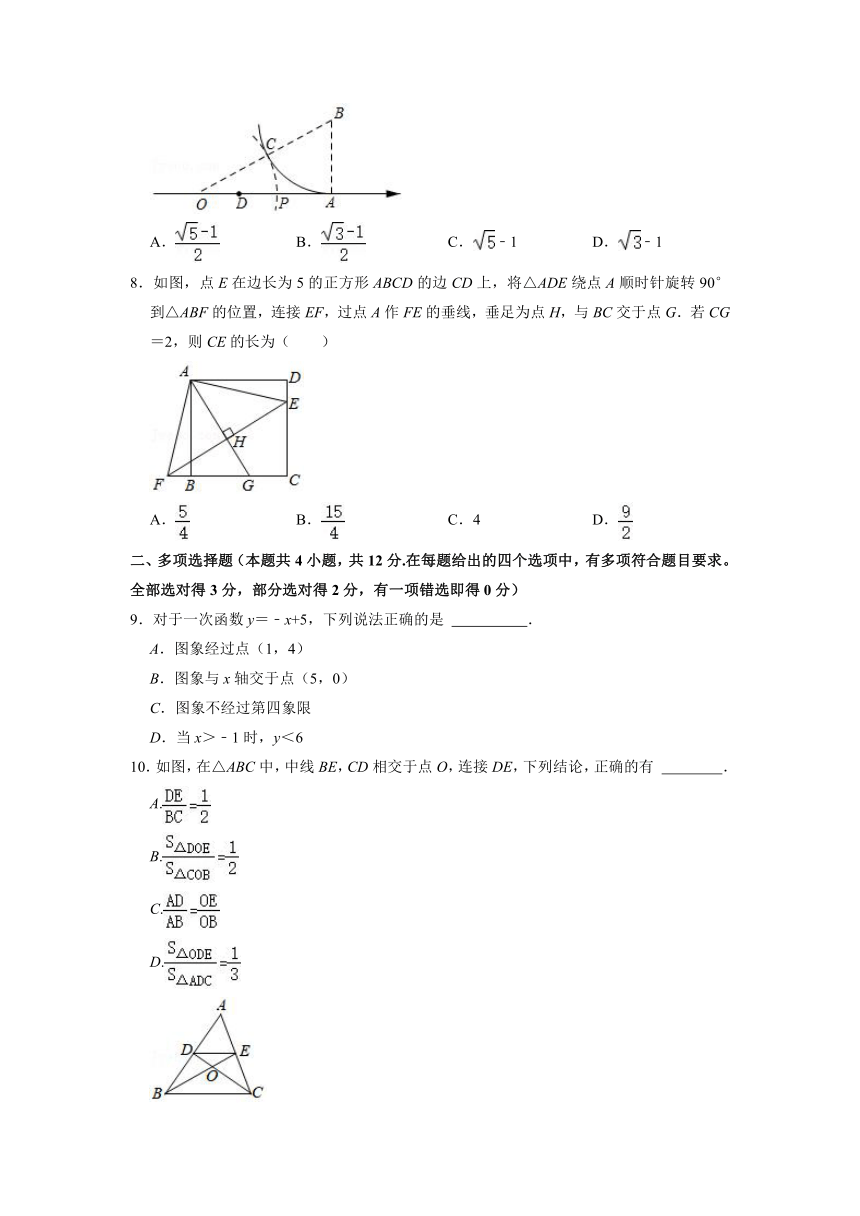
8.如图,点E在边长为5的正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作FE的垂线,垂足为点H,与BC交于点G.若CG=2,则CE的长为( )
A.
B.
C.4
D.
二、多项选择题(本题共4小题,共12分.在每题给出的四个选项中,有多项符合题目要求。全部选对得3分,部分选对得2分,有一项错选即得0分)
9.对于一次函数y=﹣x+5,下列说法正确的是
.
A.图象经过点(1,4)
B.图象与x轴交于点(5,0)
C.图象不经过第四象限
D.当x>﹣1时,y<6
10.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论,正确的有
.
A.
B.
C.
D.
11.已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为
.
A.5+2
B.15
C.10+
D.15+3
12.如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转a度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F,下列结论:其中正确的有
.
A.∠CDF=a度
B.A1E=CF
C.DF=FC
D.BE=BF
三、填空题(本大题共8小题,共24分.只要求填写最后结果,每小题填对得3分.)
13.(﹣3)2的算术平方根是
.
14.在函数y=中,自变量x的取值范围是
.
15.已知一次函数y=kx+b(k≠0)的图象经过A(﹣1,2)、B(1,﹣1)两点,则k
0(填“>”或“<”).
16.不等式组的解集为
.
17.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为
.
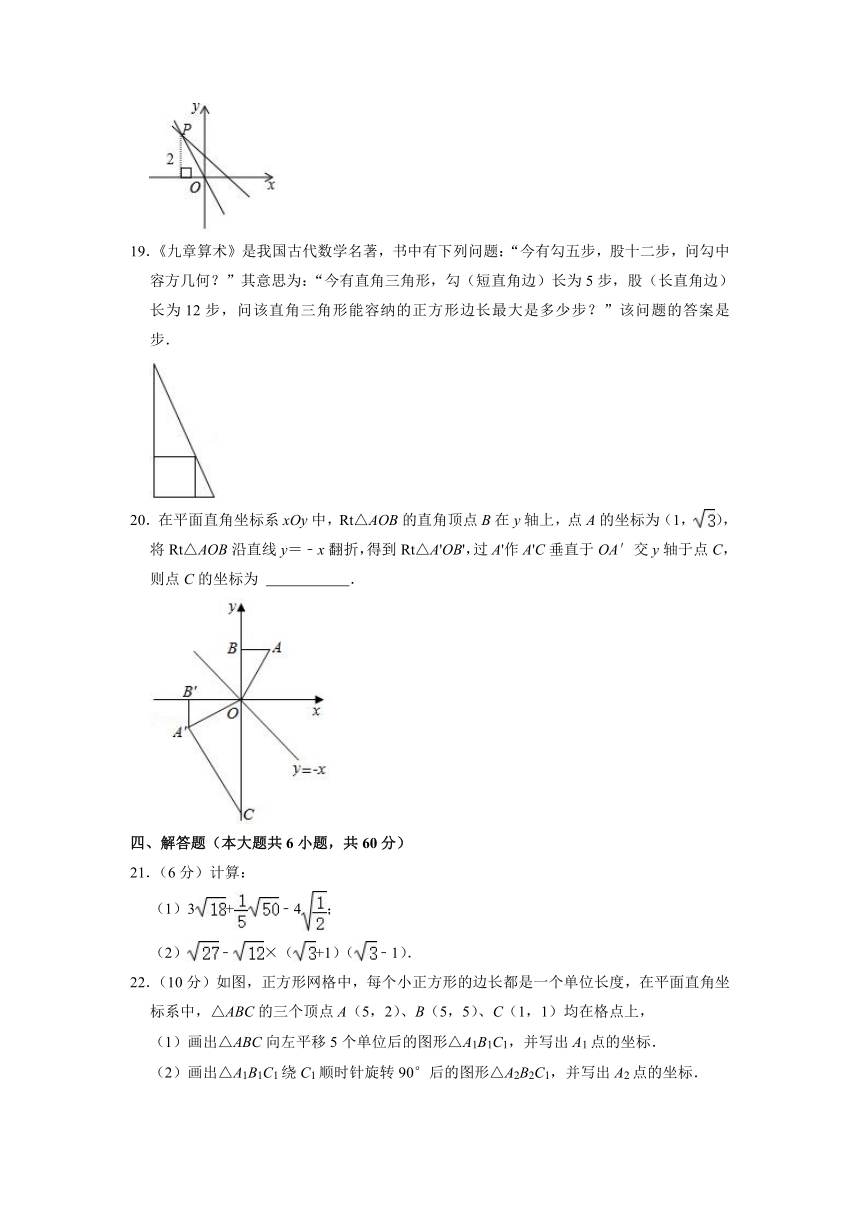
18.如图,正比例函数的图象与一次函数y=﹣x+1的图象相交于点P,点P到x轴的距离是2,则这个正比例函数的解析式是
.
19.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是
步.
20.在平面直角坐标系xOy中,Rt△AOB的直角顶点B在y轴上,点A的坐标为(1,),将Rt△AOB沿直线y=﹣x翻折,得到Rt△A'OB',过A'作A'C垂直于OA′交y轴于点C,则点C的坐标为
.
四、解答题(本大题共6小题,共60分)
21.(6分)计算:
(1)3+﹣4;
(2)﹣×(+1)(﹣1).
22.(10分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上,
(1)画出△ABC向左平移5个单位后的图形△A1B1C1,并写出A1点的坐标.
(2)画出△A1B1C1绕C1顺时针旋转90°后的图形△A2B2C1,并写出A2点的坐标.
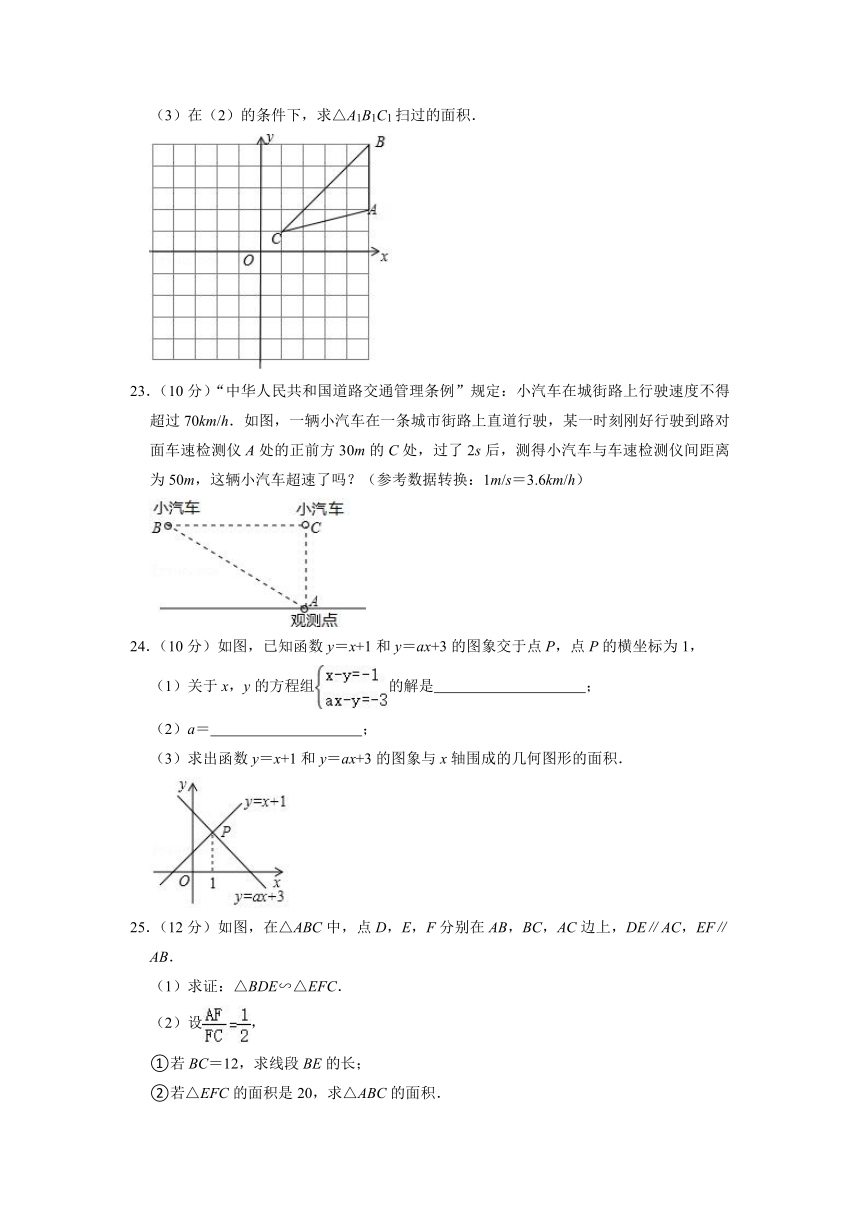
(3)在(2)的条件下,求△A1B1C1扫过的面积.
23.(10分)“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
24.(10分)如图,已知函数y=x+1和y=ax+3的图象交于点P,点P的横坐标为1,
(1)关于x,y的方程组的解是
;
(2)a=
;
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积.
25.(12分)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
26.(12分)为了做好新冠的个人防疫,小明妈妈联合班级其他同学的家长去药店团购口罩.口罩原来一包是20元,由于家长们购买的数量比较多,药店老板决定给他们优惠,
方式如下:
方式一:每包口罩打九折;
方式二:如果购买的口罩不超过40包,则口罩按原价销售,如果购买的口罩超过40包,则超出的部分打八折销售.
设大家一共需要团购口罩x包,
(1)口罩的总费用为y元,请分别求出两种方式y与x的关系式;
(2)已知每位家长为孩子都准备5包口罩,小明妈妈根据联合家长的人数如何选择优惠方式?
2020-2021学年山东省潍坊市安丘市八年级(下)期末数学试卷
参考答案与试题解析
一、单项选择题(每小题3分,共24分.每小题给出的四个选项中只有一项是正确的)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
A.赵爽弦图
B.笛卡尔心形线
C.科克曲线
D.斐波那契螺旋线
【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:A、不是轴对称图形,是中心对称图形,故此选项错误;
B、是轴对称图形,不是中心对称图形,故此选项错误;
C、是轴对称图形,是中心对称图形,故此选项正确;
D、不是轴对称图形,不是中心对称图形,故此选项错误;
故选:C.
2.的相反数是( )
A.﹣3
B.3
C.
D.﹣9
【分析】利用二次根式的性质结合相反数的概念求解.
【解答】解:,
3的相反数是﹣3,
故选:A.
3.下列属于最简二次根式的是( )
A.
B.
C.
D.
【分析】最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式,据此进行判断.
【解答】解:A、=2,故此选项不符合题意;
B、,故此选项不符合题意;
C、是最简二次根式,故此选项符合题意;
D、,故此选项不符合题意;
故选:C.
4.一根1m长的木杆,竖直放置在地面上,影长为1.5m,同一时刻,一棵树落在地面上的影长为12m,则树高为( )
A.6m
B.8m
C.12m
D.18m
【分析】设树高为xm.同一时刻任何物体的高与其影子的比值是相同的,所以竹竿的高与其影子的比值和树高与其影子的比值相同,利用这个结论可以求出树高.
【解答】解:设树高为xm.
由题意,=,
∴x=8,
∴树高为8m.
故选:B.
5.一次函数y=mx﹣m(m为常数且m≠0),若y随x增大而增大,则它的图象经过( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
【分析】根据一次函数的性质得:y随x增大而增大,则m>0,于是得到一次函数y=mx﹣m经过第一、三象限,且与y轴的交点在x轴下方,即可得答案.
【解答】解:∵一次函数y=mx﹣m(m为常数且m≠0),y随x增大而增大,
∴m>0,
∴一次函数y=mx﹣m经过第一、三象限,且与y轴的交点在x轴下方,即图象还经过第四象限,
故选:C.
6.如图,函数y=3x和y=ax+4的图象相交于点A(m,3),则不等式3x≤ax+4的解集为( )
A.x≥1
B.x≤1
C.x≤3
D.x≥3
【分析】首先把(m,3)代入y=3x求得m的值,然后根据函数的图象即可写出不等式的解集.
【解答】解:把A(m,3)代入y=3x,得:3m=3,解得:m=1;
根据图象可得:不等式3x≤ax+4的解集是:x≤1.
故选:B.
7.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A.
B.
C.﹣1
D.﹣1
【分析】根据勾股定理求出OB,求出BC=AB=1,求出OC=OP=﹣1,再根据线段的中点定义求出OD即可.
【解答】解:在Rt△OAB中,∠OAB=90°,AB=1,OA=2,由勾股定理得:OB==,
∵BC=AB,AB=1,
∴BC=1,
∴OC=OB﹣BC=﹣1,
即OP=﹣1,
∵OP的中点是D,
∴OD=OP=×(﹣1)=,
即点D表示的数是,
故选:A.
8.如图,点E在边长为5的正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作FE的垂线,垂足为点H,与BC交于点G.若CG=2,则CE的长为( )
A.
B.
C.4
D.
【分析】连接EG,根据AG垂直平分EF,即可得出EG=FG,设CE=x,则DE=5﹣x=BF,FG=EG=8﹣x,再根据Rt△CEG中,CE2+CG2=EG2,即可得到CE的长.
【解答】解:如图所示,连接EG,
由旋转可得,△ADE≌△ABF,
∴AE=AF,DE=BF,
又∵AG⊥EF,
∴H为EF的中点,
∴AG垂直平分EF,
∴EG=FG,
设CE=x,则DE=5﹣x=BF,FG=8﹣x,
∴EG=8﹣x,
∵∠C=90°,
∴Rt△CEG中,CE2+CG2=EG2,即x2+22=(8﹣x)2,
解得x=,
∴CE的长为,
故选:B.
二、多项选择题(本题共4小题,共12分.在每题给出的四个选项中,有多项符合题目要求。全部选对得3分,部分选对得2分,有一项错选即得0分)
9.对于一次函数y=﹣x+5,下列说法正确的是
A、B、D .
A.图象经过点(1,4)
B.图象与x轴交于点(5,0)
C.图象不经过第四象限
D.当x>﹣1时,y<6
【分析】根据一次函数的性质逐个判断即可.
【解答】解:A、在y=﹣x+5中,当x=1时,y=4,故一次函数y=﹣x+5图象经过(1,4),符合题意;
B、在y=﹣x+5中,当y=0时,x=5,故一次函数y=﹣x+5图象与x轴交于(5,0),符合题意;
C、一次函数y=﹣x+5中,k=﹣1<0,b=5>0,故一次函数y=﹣x+5图象经过一、二、四象限,不符合题意;
D、由x>﹣1得﹣x<1,从而﹣x+5<6,故y<6,符合题意;
故答案为:A、B、D.
10.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论,正确的有
A、C .
A.
B.
C.
D.
【分析】由中线BE和中线CD得DE是△ABC的中位线,由中位线的性质判断A,B;由中位线得证△DOE∽△COB,从而判断C;由重心的性质得△ODE与△ABC的面积关系,由中线CD得△ADC和△ABC的面积关系,从而判断D.
【解答】解:A、∵BE和CD是△ABC的中线,
∴DE是△ABC的中位线,点O是△ABC的重心,
∴DE:BC=1:2,故选项A正确,符合题意;
AD:AB=1:2,DE∥BC,
∴∠OED=∠OBC,∠ODE=∠OCB,
∴△OED∽△OBC,
∴,故选项B错误,不符合题意;
OE:OB=ED:BC=1:2,
∴AD:AB=OE:OB,故选项C正确,符合题意;
∵点O是△ABC的重心,
∴S△BOC=S△ABC,
∴S△DOE=S△BOC=?S△ABC=S△ABC,
∵CD是△ABC的中线,
∴S△ADC=S△ABC,
∴S△DOE:S△ADC=S△ABC:S△ABC=1:6,故选项D错误,不符合题意;
故答案为:A、C.
11.已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为
A、C .
A.5+2
B.15
C.10+
D.15+3
【分析】根据相似三角形的性质、分情况计算即可.
【解答】解:当3,4为直角边,6,8也为直角边时,此时两三角形相似;
当三边分别为3,4,,和6,8,2,此时两三角形相似;
当3,4为直角边时,m=5;则8为另一三角形的斜边,其直角边为:n==2,
故m+n=5+2;
当6,8为直角边,n=10;则4为另一三角形的斜边,其直角边为:m==,
故m+n=10+;
综上所述:m+n的值为5+2或10+,
故选:A、C.
12.如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转a度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F,下列结论:其中正确的有
ABD .
A.∠CDF=a度
B.A1E=CF
C.DF=FC
D.BE=BF
【分析】根据等腰三角形的性质由BA=BC得∠A=∠C,再根据旋转的性质得BA=BA1=BC=BC1,∠ABA1=∠CBC1=α,∠A=∠A1=∠C=∠C1,而根据对顶角相等得∠BFC1=∠DFC,于是可根据三角形内角和定理得到∠CDF=∠FBC1=α;利用“ASA”证明△BAE≌△BC1F,则BE=BF,所以A1E=CF;由于∠CDF=α,则只有当旋转角等于∠C时才有DF=FC.
【解答】解:∵BA=BC,
∴∠A=∠C,
∵△ABC绕点B顺时针旋转α度,得到△A1BC1,
∴BA=BA1,BC=BC1,∠ABA1=∠CBC1=α,∠A=∠A1=∠C=∠C1,
∵∠BFC1=∠DFC,
∴∠CDF=∠FBC1=α,所以A正确,
∴BA=BA1=BC=BC1,
在△BAE和△BC1F中
,
∴△BAE≌△BC1F(ASA),
∴BE=BF,故D正确
而BA1=BC,
∴A1E=CF,所以B正确;
∵∠CDF=α,
∴当旋转角等于∠C时,DF=FC,所以C错误;
故答案为ABD.
三、填空题(本大题共8小题,共24分.只要求填写最后结果,每小题填对得3分.)
13.(﹣3)2的算术平方根是 3 .
【分析】根据算术平方根的定义即可解决问题.
【解答】解:∵(﹣3)2=9,
∴(﹣3)2的算术平方根是3.
故答案为:3.
14.在函数y=中,自变量x的取值范围是
x≥﹣1且x≠0 .
【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
【解答】解:根据题意得:x+1≥0且x≠0,
解得:x≥﹣1且x≠0.
故答案为:x≥﹣1且x≠0.
15.已知一次函数y=kx+b(k≠0)的图象经过A(﹣1,2)、B(1,﹣1)两点,则k < 0(填“>”或“<”).
【分析】设直线AB的解析式为:y=kx+b(k≠0),把A(﹣1,2)、B(1,﹣1)代入代入,得到k和b值,即可得到结论.
【解答】解:设直线AB的解析式为:y=kx+b(k≠0),
把A(﹣1,2)、B(1,﹣1)代入y=kx+b得,
,
解得:k=﹣,b=,
∴k<0,
解法二:由A(﹣1,2)、B(1,﹣1)可知,随着x的减小,y反而增大,所以有k<0.
故答案为:<.
16.不等式组的解集为
x>5 .
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式2x﹣6>0,得:x>3,
解不等式4﹣x<﹣1,得:x>5,
则不等式组的解集为x>5,
故答案为:x>5.
17.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为 1 .
【分析】利用平移的性质得到BE=CF,然后利用EC=2BE=2得到BE的长,从而得到CF的长.
【解答】解:∵△ABC沿BC方向平移至△DEF处.
∴BE=CF,
∵EC=2BE=2,
∴BE=1,
∴CF=1.
故答案为1.
18.如图,正比例函数的图象与一次函数y=﹣x+1的图象相交于点P,点P到x轴的距离是2,则这个正比例函数的解析式是 y=﹣2x .
【分析】根据图象和题意,可以得到点P的纵坐标,然后代入一次函数解析式,即可得到点P的坐标,然后代入正比例函数解析式,即可得到这个正比例函数的解析式.
【解答】解:∵点P到x轴的距离为2,
∴点P的纵坐标为2,
∵点P在一次函数y=﹣x+1的图象上,
∴2=﹣x+1,得x=﹣1,
∴点P的坐标为(﹣1,2),
设正比例函数解析式为y=kx,
则2=﹣k,得k=﹣2,
∴正比例函数解析式为y=﹣2x,
故答案为:y=﹣2x.
19.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
【分析】如图1,根据正方形的性质得:DE∥BC,则△ADE∽△ACB,列比例式可得结论;如图2,同理可得正方形的边长,比较可得最大值.
【解答】解:如图1,∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=12﹣x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴,
∴,
x=,
如图2,四边形DGFE是正方形,
过C作CP⊥AB于P,交DG于Q,
设ED=x,
S△ABC=AC?BC=AB?CP,
12×5=13CP,
CP=,
同理得:△CDG∽△CAB,
∴,
∴,
x=,
∴该直角三角形能容纳的正方形边长最大是(步),
故答案为:.
20.在平面直角坐标系xOy中,Rt△AOB的直角顶点B在y轴上,点A的坐标为(1,),将Rt△AOB沿直线y=﹣x翻折,得到Rt△A'OB',过A'作A'C垂直于OA′交y轴于点C,则点C的坐标为
(0,﹣4) .
【分析】依据轴对称的性质可得OB'=OB=,A′B′=AB=1,OA′=OA=2,进而通过证得△A′OB′∽△COA′,求得OC=4,即可证得C的坐标为(0,﹣4).
【解答】解:∵点A的坐标为(1,),
∴AB=1,OB=,
∴OA===2,
∵将Rt△AOB沿直线y=﹣x翻折,得到Rt△A'OB',
∴OB'=OB=,A′B′=AB=1,OA′=OA=2,
∴A'(﹣,﹣1),
∵过A'作A'C垂直于OA'交y轴于点C,
∴∠A′OC+∠A′CO=90°,
∵∠A′OB′+∠A′OC=90°,
∴∠A′CO=∠A′OB′,
∵∠A′B′O=∠OA′C=90°,
∴△A′OB′∽△OCA′,
∴=,即=,
∴OC=4,
∴C(0,﹣4),
故答案是:(0,﹣4).
四、解答题(本大题共6小题,共60分)
21.(6分)计算:
(1)3+﹣4;
(2)﹣×(+1)(﹣1).
【分析】(1)先化简二次根式,然后先算乘法,再算加减;
(2)先利用平方差公式算乘法,然后化简二次根式,先算小括号里面的,然后算乘法,最后算减法.
【解答】解:(1)原式=3×+﹣4×
=9+﹣2
=8;
(2)原式=3﹣2[()2﹣12]
=3﹣2×2
=3﹣4
=﹣.
22.(10分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上,
(1)画出△ABC向左平移5个单位后的图形△A1B1C1,并写出A1点的坐标.
(2)画出△A1B1C1绕C1顺时针旋转90°后的图形△A2B2C1,并写出A2点的坐标.
(3)在(2)的条件下,求△A1B1C1扫过的面积.
【分析】(1)利用普遍化的性质分别作出A,B,C的对应点A1,B1,C1即可.
(2)利用旋转变换的性质分别作出A1,B1的对应点A2,B2.
(3)△A1B1C1扫过的面积可以看成扇形面积与三角形的面积的和.
【解答】解:(1)ΔA1B1C1如图所示,A1(0,2);
(2)ΔA2B2C1如图所示,A2(﹣3,﹣3);
(3)∵,
∴.
23.(10分)“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
【分析】本题求小汽车是否超速,其实就是求BC的距离,直角三角形ABC中,有斜边AB的长,有直角边AC的长,那么BC的长就很容易求得,根据小汽车用2s行驶的路程为BC,那么可求出小汽车的速度,然后再判断是否超速了.
【解答】解:在Rt△ABC中,AC=30m,AB=50m;
根据勾股定理可得:
(m)
∴小汽车的速度为v==20(m/s)=20×3.6(km/h)=72(km/h);
∵72(km/h)>70(km/h);
∴这辆小汽车超速行驶.
答:这辆小汽车超速了.
24.(10分)如图,已知函数y=x+1和y=ax+3的图象交于点P,点P的横坐标为1,
(1)关于x,y的方程组的解是 ;
(2)a= ﹣1 ;
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积.
【分析】(1)先把x=1代入y=x+1,得出y=2,则两个一次函数的交点P的坐标为(1,2);那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解;
(2)把P(1,2)代入y=ax+3即可得到结论;
(3)分别求出函数y=x+1和y=ax+3的图象与x轴的交点坐标,再根据三角形的面积公式列式计算即可.
【解答】解:(1)把x=1代入y=x+1,得出y=2,
函数y=x+1和y=ax+3的图象交于点P(1,2),
即x=1,y=2同时满足两个一次函数的解析式.
所以关于x,y的方程组的解是.
故答案为;
(2)把P(1,2)代入y=ax+3,
得2=a+3,解得a=﹣1.
故答案为﹣1;
(3)∵函数y=x+1与x轴的交点为(﹣1,0),
y=﹣x+3与x轴的交点为(3,0),
∴这两个交点之间的距离为3﹣(﹣1)=4,
∵P(1,2),
∴函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积为:×4×2=4.
25.(12分)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
【分析】(1)由平行线的性质得出∠DEB=∠FCE,∠DBE=∠FEC,即可得出结论;
(2)①由平行线的性质得出==,即可得出结果;
②先求出=,易证△EFC∽△BAC,由相似三角形的面积比等于相似比的平方即可得出结果.
【解答】(1)证明:∵DE∥AC,
∴∠DEB=∠FCE,
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC;
(2)解:①∵EF∥AB,
∴==,
∵EC=BC﹣BE=12﹣BE,
∴=,
解得:BE=4;
②∵=,
∴=,
∵EF∥AB,
∴△EFC∽△BAC,
∴=()2=()2=,
∴S△ABC=S△EFC=×20=45.
26.(12分)为了做好新冠的个人防疫,小明妈妈联合班级其他同学的家长去药店团购口罩.口罩原来一包是20元,由于家长们购买的数量比较多,药店老板决定给他们优惠,
方式如下:
方式一:每包口罩打九折;
方式二:如果购买的口罩不超过40包,则口罩按原价销售,如果购买的口罩超过40包,则超出的部分打八折销售.
设大家一共需要团购口罩x包,
(1)口罩的总费用为y元,请分别求出两种方式y与x的关系式;
(2)已知每位家长为孩子都准备5包口罩,小明妈妈根据联合家长的人数如何选择优惠方式?
【分析】(1)根据题意,可以分别写出方式一和方式二中y与x的函数关系式;
(2)根据题意,可以计算出当x为多少时,两种方式花费一样多,从而可以得到小明妈妈根据联合家长的人数如何选择优惠方式.
【解答】解:(1)由题意可得,
方式一:y与x的函数关系式为y=20×0.9x=18x;
方式二:当0≤x≤40时,y=20x,
当x>40时,y=20×40+20×0.8(x﹣40)=16x+160,
由上可得,y=;
(2)由题意可得,当0≤x≤40时,选择方式一,
当x>40时,令18x=16x+160,解得x=80,
∵80÷5=16,
∴当家长人数小于16时,选择方式一,
当家长人数等于16时,选择方式一和方式二一样,
当家长人数大于16时,选择方式二.
一、单项选择题(每小题3分,共24分.每小题给出的四个选项中只有一项是正确的)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
A.赵爽弦图
B.笛卡尔心形线
C.科克曲线
D.斐波那契螺旋线
2.的相反数是( )
A.﹣3
B.3
C.
D.﹣9
3.下列属于最简二次根式的是( )
A.
B.
C.
D.
4.一根1m长的木杆,竖直放置在地面上,影长为1.5m,同一时刻,一棵树落在地面上的影长为12m,则树高为( )
A.6m
B.8m
C.12m
D.18m
5.一次函数y=mx﹣m(m为常数且m≠0),若y随x增大而增大,则它的图象经过( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
6.如图,函数y=3x和y=ax+4的图象相交于点A(m,3),则不等式3x≤ax+4的解集为( )
A.x≥1
B.x≤1
C.x≤3
D.x≥3
7.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A.
B.
C.﹣1
D.﹣1
8.如图,点E在边长为5的正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作FE的垂线,垂足为点H,与BC交于点G.若CG=2,则CE的长为( )
A.
B.
C.4
D.
二、多项选择题(本题共4小题,共12分.在每题给出的四个选项中,有多项符合题目要求。全部选对得3分,部分选对得2分,有一项错选即得0分)
9.对于一次函数y=﹣x+5,下列说法正确的是
.
A.图象经过点(1,4)
B.图象与x轴交于点(5,0)
C.图象不经过第四象限
D.当x>﹣1时,y<6
10.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论,正确的有
.
A.
B.
C.
D.
11.已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为
.
A.5+2
B.15
C.10+
D.15+3
12.如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转a度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F,下列结论:其中正确的有
.
A.∠CDF=a度
B.A1E=CF
C.DF=FC
D.BE=BF
三、填空题(本大题共8小题,共24分.只要求填写最后结果,每小题填对得3分.)
13.(﹣3)2的算术平方根是
.
14.在函数y=中,自变量x的取值范围是
.
15.已知一次函数y=kx+b(k≠0)的图象经过A(﹣1,2)、B(1,﹣1)两点,则k
0(填“>”或“<”).
16.不等式组的解集为
.
17.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为
.
18.如图,正比例函数的图象与一次函数y=﹣x+1的图象相交于点P,点P到x轴的距离是2,则这个正比例函数的解析式是
.
19.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是
步.
20.在平面直角坐标系xOy中,Rt△AOB的直角顶点B在y轴上,点A的坐标为(1,),将Rt△AOB沿直线y=﹣x翻折,得到Rt△A'OB',过A'作A'C垂直于OA′交y轴于点C,则点C的坐标为
.
四、解答题(本大题共6小题,共60分)
21.(6分)计算:
(1)3+﹣4;
(2)﹣×(+1)(﹣1).
22.(10分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上,
(1)画出△ABC向左平移5个单位后的图形△A1B1C1,并写出A1点的坐标.
(2)画出△A1B1C1绕C1顺时针旋转90°后的图形△A2B2C1,并写出A2点的坐标.
(3)在(2)的条件下,求△A1B1C1扫过的面积.
23.(10分)“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
24.(10分)如图,已知函数y=x+1和y=ax+3的图象交于点P,点P的横坐标为1,
(1)关于x,y的方程组的解是
;
(2)a=
;
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积.
25.(12分)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
26.(12分)为了做好新冠的个人防疫,小明妈妈联合班级其他同学的家长去药店团购口罩.口罩原来一包是20元,由于家长们购买的数量比较多,药店老板决定给他们优惠,
方式如下:
方式一:每包口罩打九折;
方式二:如果购买的口罩不超过40包,则口罩按原价销售,如果购买的口罩超过40包,则超出的部分打八折销售.
设大家一共需要团购口罩x包,
(1)口罩的总费用为y元,请分别求出两种方式y与x的关系式;
(2)已知每位家长为孩子都准备5包口罩,小明妈妈根据联合家长的人数如何选择优惠方式?
2020-2021学年山东省潍坊市安丘市八年级(下)期末数学试卷
参考答案与试题解析
一、单项选择题(每小题3分,共24分.每小题给出的四个选项中只有一项是正确的)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
A.赵爽弦图
B.笛卡尔心形线
C.科克曲线
D.斐波那契螺旋线
【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:A、不是轴对称图形,是中心对称图形,故此选项错误;
B、是轴对称图形,不是中心对称图形,故此选项错误;
C、是轴对称图形,是中心对称图形,故此选项正确;
D、不是轴对称图形,不是中心对称图形,故此选项错误;
故选:C.
2.的相反数是( )
A.﹣3
B.3
C.
D.﹣9
【分析】利用二次根式的性质结合相反数的概念求解.
【解答】解:,
3的相反数是﹣3,
故选:A.
3.下列属于最简二次根式的是( )
A.
B.
C.
D.
【分析】最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式,据此进行判断.
【解答】解:A、=2,故此选项不符合题意;
B、,故此选项不符合题意;
C、是最简二次根式,故此选项符合题意;
D、,故此选项不符合题意;
故选:C.
4.一根1m长的木杆,竖直放置在地面上,影长为1.5m,同一时刻,一棵树落在地面上的影长为12m,则树高为( )
A.6m
B.8m
C.12m
D.18m
【分析】设树高为xm.同一时刻任何物体的高与其影子的比值是相同的,所以竹竿的高与其影子的比值和树高与其影子的比值相同,利用这个结论可以求出树高.
【解答】解:设树高为xm.
由题意,=,
∴x=8,
∴树高为8m.
故选:B.
5.一次函数y=mx﹣m(m为常数且m≠0),若y随x增大而增大,则它的图象经过( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
【分析】根据一次函数的性质得:y随x增大而增大,则m>0,于是得到一次函数y=mx﹣m经过第一、三象限,且与y轴的交点在x轴下方,即可得答案.
【解答】解:∵一次函数y=mx﹣m(m为常数且m≠0),y随x增大而增大,
∴m>0,
∴一次函数y=mx﹣m经过第一、三象限,且与y轴的交点在x轴下方,即图象还经过第四象限,
故选:C.
6.如图,函数y=3x和y=ax+4的图象相交于点A(m,3),则不等式3x≤ax+4的解集为( )
A.x≥1
B.x≤1
C.x≤3
D.x≥3
【分析】首先把(m,3)代入y=3x求得m的值,然后根据函数的图象即可写出不等式的解集.
【解答】解:把A(m,3)代入y=3x,得:3m=3,解得:m=1;
根据图象可得:不等式3x≤ax+4的解集是:x≤1.
故选:B.
7.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A.
B.
C.﹣1
D.﹣1
【分析】根据勾股定理求出OB,求出BC=AB=1,求出OC=OP=﹣1,再根据线段的中点定义求出OD即可.
【解答】解:在Rt△OAB中,∠OAB=90°,AB=1,OA=2,由勾股定理得:OB==,
∵BC=AB,AB=1,
∴BC=1,
∴OC=OB﹣BC=﹣1,
即OP=﹣1,
∵OP的中点是D,
∴OD=OP=×(﹣1)=,
即点D表示的数是,
故选:A.
8.如图,点E在边长为5的正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作FE的垂线,垂足为点H,与BC交于点G.若CG=2,则CE的长为( )
A.
B.
C.4
D.
【分析】连接EG,根据AG垂直平分EF,即可得出EG=FG,设CE=x,则DE=5﹣x=BF,FG=EG=8﹣x,再根据Rt△CEG中,CE2+CG2=EG2,即可得到CE的长.
【解答】解:如图所示,连接EG,
由旋转可得,△ADE≌△ABF,
∴AE=AF,DE=BF,
又∵AG⊥EF,
∴H为EF的中点,
∴AG垂直平分EF,
∴EG=FG,
设CE=x,则DE=5﹣x=BF,FG=8﹣x,
∴EG=8﹣x,
∵∠C=90°,
∴Rt△CEG中,CE2+CG2=EG2,即x2+22=(8﹣x)2,
解得x=,
∴CE的长为,
故选:B.
二、多项选择题(本题共4小题,共12分.在每题给出的四个选项中,有多项符合题目要求。全部选对得3分,部分选对得2分,有一项错选即得0分)
9.对于一次函数y=﹣x+5,下列说法正确的是
A、B、D .
A.图象经过点(1,4)
B.图象与x轴交于点(5,0)
C.图象不经过第四象限
D.当x>﹣1时,y<6
【分析】根据一次函数的性质逐个判断即可.
【解答】解:A、在y=﹣x+5中,当x=1时,y=4,故一次函数y=﹣x+5图象经过(1,4),符合题意;
B、在y=﹣x+5中,当y=0时,x=5,故一次函数y=﹣x+5图象与x轴交于(5,0),符合题意;
C、一次函数y=﹣x+5中,k=﹣1<0,b=5>0,故一次函数y=﹣x+5图象经过一、二、四象限,不符合题意;
D、由x>﹣1得﹣x<1,从而﹣x+5<6,故y<6,符合题意;
故答案为:A、B、D.
10.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论,正确的有
A、C .
A.
B.
C.
D.
【分析】由中线BE和中线CD得DE是△ABC的中位线,由中位线的性质判断A,B;由中位线得证△DOE∽△COB,从而判断C;由重心的性质得△ODE与△ABC的面积关系,由中线CD得△ADC和△ABC的面积关系,从而判断D.
【解答】解:A、∵BE和CD是△ABC的中线,
∴DE是△ABC的中位线,点O是△ABC的重心,
∴DE:BC=1:2,故选项A正确,符合题意;
AD:AB=1:2,DE∥BC,
∴∠OED=∠OBC,∠ODE=∠OCB,
∴△OED∽△OBC,
∴,故选项B错误,不符合题意;
OE:OB=ED:BC=1:2,
∴AD:AB=OE:OB,故选项C正确,符合题意;
∵点O是△ABC的重心,
∴S△BOC=S△ABC,
∴S△DOE=S△BOC=?S△ABC=S△ABC,
∵CD是△ABC的中线,
∴S△ADC=S△ABC,
∴S△DOE:S△ADC=S△ABC:S△ABC=1:6,故选项D错误,不符合题意;
故答案为:A、C.
11.已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为
A、C .
A.5+2
B.15
C.10+
D.15+3
【分析】根据相似三角形的性质、分情况计算即可.
【解答】解:当3,4为直角边,6,8也为直角边时,此时两三角形相似;
当三边分别为3,4,,和6,8,2,此时两三角形相似;
当3,4为直角边时,m=5;则8为另一三角形的斜边,其直角边为:n==2,
故m+n=5+2;
当6,8为直角边,n=10;则4为另一三角形的斜边,其直角边为:m==,
故m+n=10+;
综上所述:m+n的值为5+2或10+,
故选:A、C.
12.如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转a度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F,下列结论:其中正确的有
ABD .
A.∠CDF=a度
B.A1E=CF
C.DF=FC
D.BE=BF
【分析】根据等腰三角形的性质由BA=BC得∠A=∠C,再根据旋转的性质得BA=BA1=BC=BC1,∠ABA1=∠CBC1=α,∠A=∠A1=∠C=∠C1,而根据对顶角相等得∠BFC1=∠DFC,于是可根据三角形内角和定理得到∠CDF=∠FBC1=α;利用“ASA”证明△BAE≌△BC1F,则BE=BF,所以A1E=CF;由于∠CDF=α,则只有当旋转角等于∠C时才有DF=FC.
【解答】解:∵BA=BC,
∴∠A=∠C,
∵△ABC绕点B顺时针旋转α度,得到△A1BC1,
∴BA=BA1,BC=BC1,∠ABA1=∠CBC1=α,∠A=∠A1=∠C=∠C1,
∵∠BFC1=∠DFC,
∴∠CDF=∠FBC1=α,所以A正确,
∴BA=BA1=BC=BC1,
在△BAE和△BC1F中
,
∴△BAE≌△BC1F(ASA),
∴BE=BF,故D正确
而BA1=BC,
∴A1E=CF,所以B正确;
∵∠CDF=α,
∴当旋转角等于∠C时,DF=FC,所以C错误;
故答案为ABD.
三、填空题(本大题共8小题,共24分.只要求填写最后结果,每小题填对得3分.)
13.(﹣3)2的算术平方根是 3 .
【分析】根据算术平方根的定义即可解决问题.
【解答】解:∵(﹣3)2=9,
∴(﹣3)2的算术平方根是3.
故答案为:3.
14.在函数y=中,自变量x的取值范围是
x≥﹣1且x≠0 .
【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
【解答】解:根据题意得:x+1≥0且x≠0,
解得:x≥﹣1且x≠0.
故答案为:x≥﹣1且x≠0.
15.已知一次函数y=kx+b(k≠0)的图象经过A(﹣1,2)、B(1,﹣1)两点,则k < 0(填“>”或“<”).
【分析】设直线AB的解析式为:y=kx+b(k≠0),把A(﹣1,2)、B(1,﹣1)代入代入,得到k和b值,即可得到结论.
【解答】解:设直线AB的解析式为:y=kx+b(k≠0),
把A(﹣1,2)、B(1,﹣1)代入y=kx+b得,
,
解得:k=﹣,b=,
∴k<0,
解法二:由A(﹣1,2)、B(1,﹣1)可知,随着x的减小,y反而增大,所以有k<0.
故答案为:<.
16.不等式组的解集为
x>5 .
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式2x﹣6>0,得:x>3,
解不等式4﹣x<﹣1,得:x>5,
则不等式组的解集为x>5,
故答案为:x>5.
17.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为 1 .
【分析】利用平移的性质得到BE=CF,然后利用EC=2BE=2得到BE的长,从而得到CF的长.
【解答】解:∵△ABC沿BC方向平移至△DEF处.
∴BE=CF,
∵EC=2BE=2,
∴BE=1,
∴CF=1.
故答案为1.
18.如图,正比例函数的图象与一次函数y=﹣x+1的图象相交于点P,点P到x轴的距离是2,则这个正比例函数的解析式是 y=﹣2x .
【分析】根据图象和题意,可以得到点P的纵坐标,然后代入一次函数解析式,即可得到点P的坐标,然后代入正比例函数解析式,即可得到这个正比例函数的解析式.
【解答】解:∵点P到x轴的距离为2,
∴点P的纵坐标为2,
∵点P在一次函数y=﹣x+1的图象上,
∴2=﹣x+1,得x=﹣1,
∴点P的坐标为(﹣1,2),
设正比例函数解析式为y=kx,
则2=﹣k,得k=﹣2,
∴正比例函数解析式为y=﹣2x,
故答案为:y=﹣2x.
19.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
【分析】如图1,根据正方形的性质得:DE∥BC,则△ADE∽△ACB,列比例式可得结论;如图2,同理可得正方形的边长,比较可得最大值.
【解答】解:如图1,∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=12﹣x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴,
∴,
x=,
如图2,四边形DGFE是正方形,
过C作CP⊥AB于P,交DG于Q,
设ED=x,
S△ABC=AC?BC=AB?CP,
12×5=13CP,
CP=,
同理得:△CDG∽△CAB,
∴,
∴,
x=,
∴该直角三角形能容纳的正方形边长最大是(步),
故答案为:.
20.在平面直角坐标系xOy中,Rt△AOB的直角顶点B在y轴上,点A的坐标为(1,),将Rt△AOB沿直线y=﹣x翻折,得到Rt△A'OB',过A'作A'C垂直于OA′交y轴于点C,则点C的坐标为
(0,﹣4) .
【分析】依据轴对称的性质可得OB'=OB=,A′B′=AB=1,OA′=OA=2,进而通过证得△A′OB′∽△COA′,求得OC=4,即可证得C的坐标为(0,﹣4).
【解答】解:∵点A的坐标为(1,),
∴AB=1,OB=,
∴OA===2,
∵将Rt△AOB沿直线y=﹣x翻折,得到Rt△A'OB',
∴OB'=OB=,A′B′=AB=1,OA′=OA=2,
∴A'(﹣,﹣1),
∵过A'作A'C垂直于OA'交y轴于点C,
∴∠A′OC+∠A′CO=90°,
∵∠A′OB′+∠A′OC=90°,
∴∠A′CO=∠A′OB′,
∵∠A′B′O=∠OA′C=90°,
∴△A′OB′∽△OCA′,
∴=,即=,
∴OC=4,
∴C(0,﹣4),
故答案是:(0,﹣4).
四、解答题(本大题共6小题,共60分)
21.(6分)计算:
(1)3+﹣4;
(2)﹣×(+1)(﹣1).
【分析】(1)先化简二次根式,然后先算乘法,再算加减;
(2)先利用平方差公式算乘法,然后化简二次根式,先算小括号里面的,然后算乘法,最后算减法.
【解答】解:(1)原式=3×+﹣4×
=9+﹣2
=8;
(2)原式=3﹣2[()2﹣12]
=3﹣2×2
=3﹣4
=﹣.
22.(10分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上,
(1)画出△ABC向左平移5个单位后的图形△A1B1C1,并写出A1点的坐标.
(2)画出△A1B1C1绕C1顺时针旋转90°后的图形△A2B2C1,并写出A2点的坐标.
(3)在(2)的条件下,求△A1B1C1扫过的面积.
【分析】(1)利用普遍化的性质分别作出A,B,C的对应点A1,B1,C1即可.
(2)利用旋转变换的性质分别作出A1,B1的对应点A2,B2.
(3)△A1B1C1扫过的面积可以看成扇形面积与三角形的面积的和.
【解答】解:(1)ΔA1B1C1如图所示,A1(0,2);
(2)ΔA2B2C1如图所示,A2(﹣3,﹣3);
(3)∵,
∴.
23.(10分)“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
【分析】本题求小汽车是否超速,其实就是求BC的距离,直角三角形ABC中,有斜边AB的长,有直角边AC的长,那么BC的长就很容易求得,根据小汽车用2s行驶的路程为BC,那么可求出小汽车的速度,然后再判断是否超速了.
【解答】解:在Rt△ABC中,AC=30m,AB=50m;
根据勾股定理可得:
(m)
∴小汽车的速度为v==20(m/s)=20×3.6(km/h)=72(km/h);
∵72(km/h)>70(km/h);
∴这辆小汽车超速行驶.
答:这辆小汽车超速了.
24.(10分)如图,已知函数y=x+1和y=ax+3的图象交于点P,点P的横坐标为1,
(1)关于x,y的方程组的解是 ;
(2)a= ﹣1 ;
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积.
【分析】(1)先把x=1代入y=x+1,得出y=2,则两个一次函数的交点P的坐标为(1,2);那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解;
(2)把P(1,2)代入y=ax+3即可得到结论;
(3)分别求出函数y=x+1和y=ax+3的图象与x轴的交点坐标,再根据三角形的面积公式列式计算即可.
【解答】解:(1)把x=1代入y=x+1,得出y=2,
函数y=x+1和y=ax+3的图象交于点P(1,2),
即x=1,y=2同时满足两个一次函数的解析式.
所以关于x,y的方程组的解是.
故答案为;
(2)把P(1,2)代入y=ax+3,
得2=a+3,解得a=﹣1.
故答案为﹣1;
(3)∵函数y=x+1与x轴的交点为(﹣1,0),
y=﹣x+3与x轴的交点为(3,0),
∴这两个交点之间的距离为3﹣(﹣1)=4,
∵P(1,2),
∴函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积为:×4×2=4.
25.(12分)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
【分析】(1)由平行线的性质得出∠DEB=∠FCE,∠DBE=∠FEC,即可得出结论;
(2)①由平行线的性质得出==,即可得出结果;
②先求出=,易证△EFC∽△BAC,由相似三角形的面积比等于相似比的平方即可得出结果.
【解答】(1)证明:∵DE∥AC,
∴∠DEB=∠FCE,
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC;
(2)解:①∵EF∥AB,
∴==,
∵EC=BC﹣BE=12﹣BE,
∴=,
解得:BE=4;
②∵=,
∴=,
∵EF∥AB,
∴△EFC∽△BAC,
∴=()2=()2=,
∴S△ABC=S△EFC=×20=45.
26.(12分)为了做好新冠的个人防疫,小明妈妈联合班级其他同学的家长去药店团购口罩.口罩原来一包是20元,由于家长们购买的数量比较多,药店老板决定给他们优惠,
方式如下:
方式一:每包口罩打九折;
方式二:如果购买的口罩不超过40包,则口罩按原价销售,如果购买的口罩超过40包,则超出的部分打八折销售.
设大家一共需要团购口罩x包,
(1)口罩的总费用为y元,请分别求出两种方式y与x的关系式;
(2)已知每位家长为孩子都准备5包口罩,小明妈妈根据联合家长的人数如何选择优惠方式?
【分析】(1)根据题意,可以分别写出方式一和方式二中y与x的函数关系式;
(2)根据题意,可以计算出当x为多少时,两种方式花费一样多,从而可以得到小明妈妈根据联合家长的人数如何选择优惠方式.
【解答】解:(1)由题意可得,
方式一:y与x的函数关系式为y=20×0.9x=18x;
方式二:当0≤x≤40时,y=20x,
当x>40时,y=20×40+20×0.8(x﹣40)=16x+160,
由上可得,y=;
(2)由题意可得,当0≤x≤40时,选择方式一,
当x>40时,令18x=16x+160,解得x=80,
∵80÷5=16,
∴当家长人数小于16时,选择方式一,
当家长人数等于16时,选择方式一和方式二一样,
当家长人数大于16时,选择方式二.
同课章节目录
