13.3等腰三角形 综合练习题 2021--2022学年人教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 13.3等腰三角形 综合练习题 2021--2022学年人教版八年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 971.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 21:41:03 | ||
图片预览



文档简介
《等腰三角形》综合练习题
一、选择题
1.若等腰三角形的两边长分别为2和5,则它的周长为
A.9
B.7
C.12
D.9或12
2.三角形三个内角的比是,则是
A.等腰三角形
B.等腰直角三角形
C.等边三角形
D.不能确定
3.已知:在中,,如要判定是等边三角形,还需添加一个条件.现有下面三种说法:
①如果添加条件“”,那么是等边三角形;
②如果添加条件“”,那么是等边三角形;
③如果添加条件“边、上的高相等”,那么是等边三角形.
上述说法中,正确的有
A.3个
B.2个
C.1个
D.0个
4.上午8时,一条船从海岛出发,以
(海里时,
的速度向正北航行,10时到达海岛处,从、望灯塔,测得,.则从海岛到灯塔的距离为
A.
B.
C.
D.
5.如图,中,,是的平分线,过作交于,若的边长为,则的周长是
A.
B.
C.
D.
6.等腰三角形周长为18,其中一边长为4,则其它两边长分别为
A.4,10
B.7,7
C.4,10或7,7
D.无法确定
7.如图在网格中,已知点、是两格点,若点也是格点,且使为等腰三角形,则点个数是
A.6
B.7
C.8
D.9
二、填空题
1.下面是由同一型号的黑白两种颜色的等边三角形瓷砖按一定规律铺设的图形,仔细观察图形可知:
第1个图形中有1块黑色的瓷砖,可表示为;
第2个图形中有3块黑色的瓷砖,可表示为;
第3个图形中有6块黑色的瓷砖,可表示为;
则第个图形中有 块黑色的瓷砖为正整数).
2.如图,直线,的顶点在直线上,边与直线相交于点.若是等边三角形,,则 .
3.如图,中,平分,平分的外角,经过点与、分别交于点、,并且.则、、之间的数量关系是 .
4.在中,,,.动点从点开始按的路径绕的边运动一周,速度为每秒,运动的时间为秒.则为等腰三角形时的值是 .
5.如图,中,,点在边上,点在边上,,,则的大小为 .
6.如图,下列4个三角形中,均有,则经过三角形的一个顶点的一条直线不能够将这个三角形分成两个小等腰三角形的是 (填序号).
三、解答题
1.如图,是等边三角形,,分别交和于点、.点是线段的中点,连接并延长交于点.
(1)求的度数.
(2)求证:.
2.已知:如图,,是上一点,于点,的延长线交的延长线于点.求证:是等腰三角形.
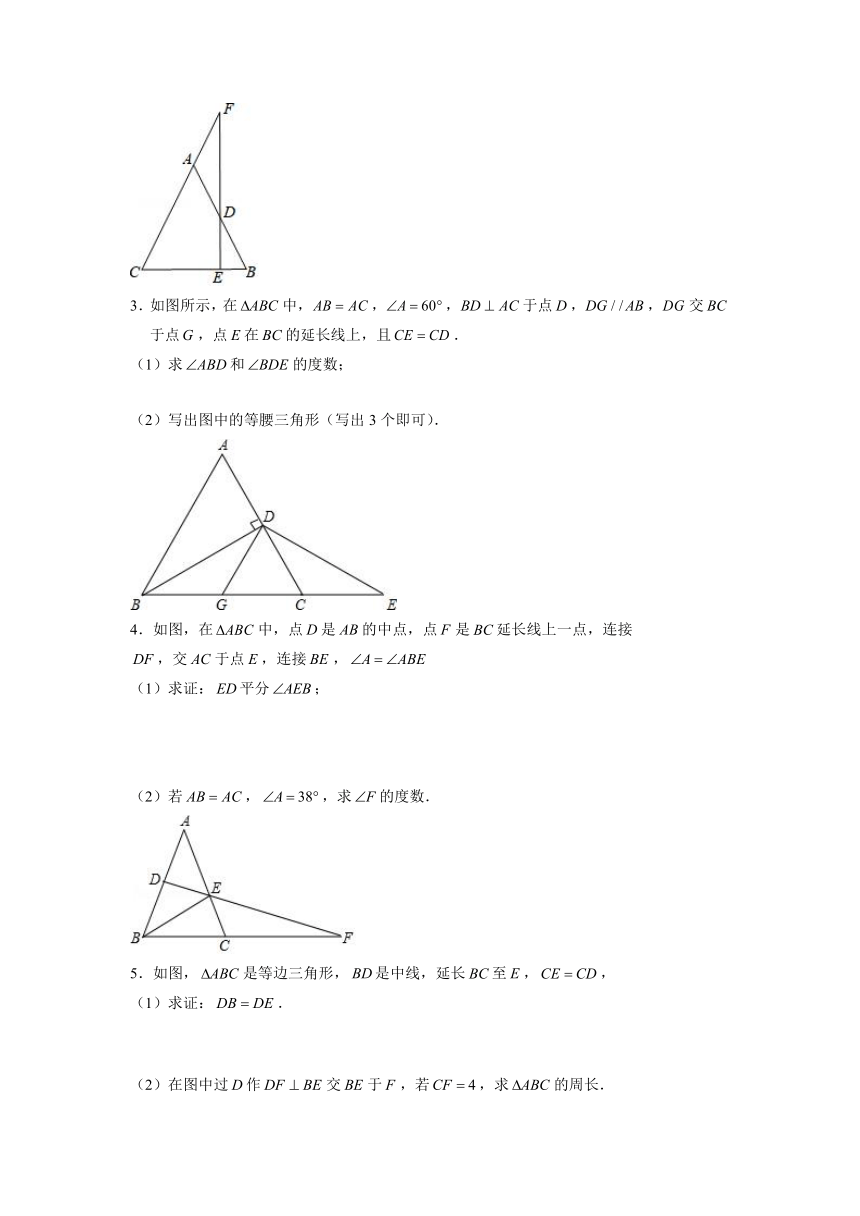
3.如图所示,在中,,,于点,,交于点,点在的延长线上,且.
(1)求和的度数;
(2)写出图中的等腰三角形(写出3个即可).
4.如图,在中,点是的中点,点是延长线上一点,连接
,交于点,连接,
(1)求证:平分;
(2)若,,求的度数.
5.如图,是等边三角形,是中线,延长至,,
(1)求证:.
(2)在图中过作交于,若,求的周长.
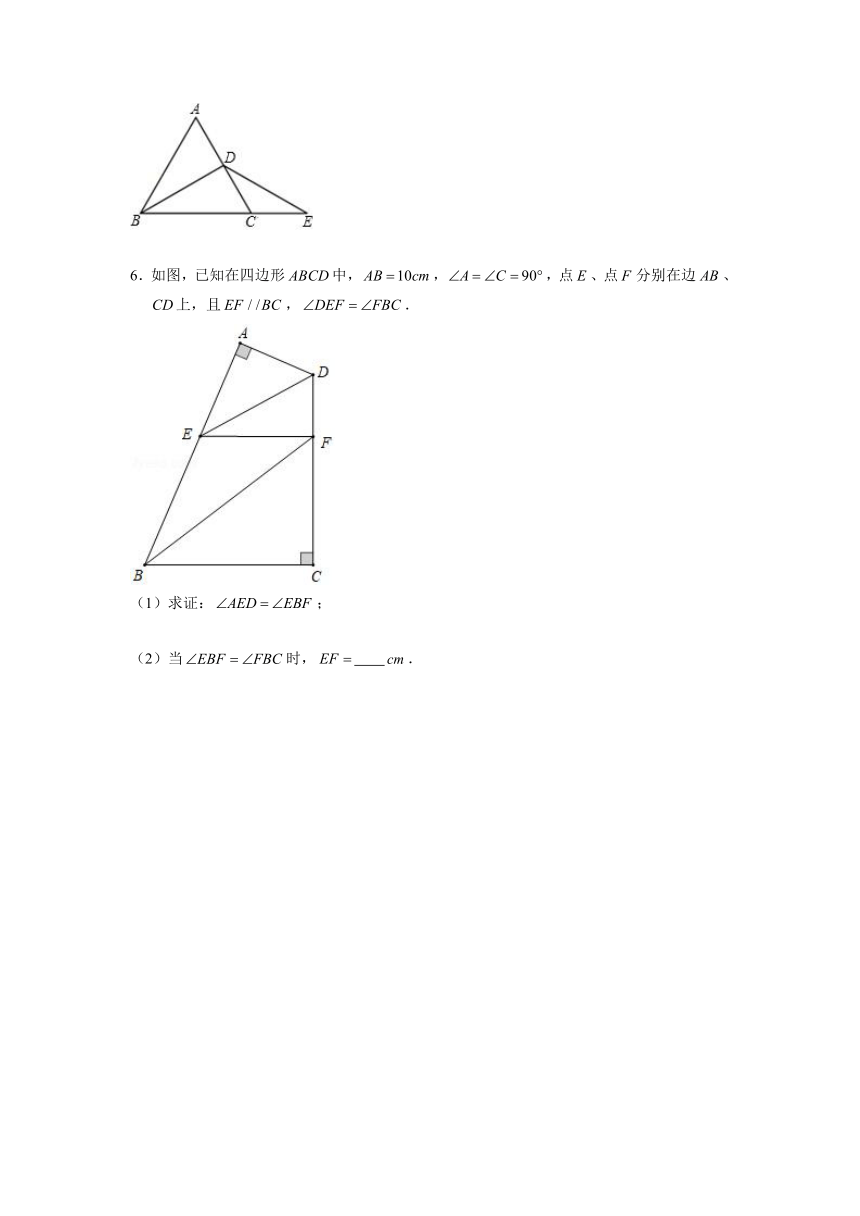
6.如图,已知在四边形中,,,点、点分别在边、上,且,.
(1)求证:;
(2)当时, .
参考答案
一、选择题
1.
【解答】解:(1)若2为腰长,5为底边长,
由于,则三角形不存在;
(2)若5为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为.
故选:.
2.
【解答】解:,,
,.
则该三角形的等腰直角三角形.
故选:.
3.
【解答】解:①若添加的条件为,由,
利用有一个角为的等腰三角形为等边三角形可得出为等边三角形;
②若添加条件为,
又,
,
,
则为等边三角形;
③若添加的条件为边、上的高相等,如图所示:
已知:,,,且,
求证:为等边三角形.
证明:,,
,
在和中,
,
,
,
,
,即为等边三角形,
综上,正确的说法有3个.
故选:.
4.
【解答】解:,,
.
,
,
上午8时,一条船从海岛出发,以
的速度向正北航行.10时到达海岛处,
.
故选:.
5.
【解答】解:是的平分线,是等边三角形,
,
,
,
,
的边长为,
的周长为,
,
解得的周长.
故选:.
6.
【解答】解:当腰为4时,另一腰也为4,则底为,
,
这样的三边不能构成三角形.
当底为4时,腰为,
,
以4,7,7为边能构成三角形
其它两边长分别为7,7.
故选:.
7.
【解答】解:如图:
①以为等腰底边时,符合条件的点有4个:分别为:,,,;
②以为等腰其中的一条腰时,符合条件的点有4个:分别为:,,,.
故选:.
二、填空题
1.
【解答】解:第个图形有:为正整数),
故答案为:.
2.
【解答】解:是等边三角形,
,
,
,
由三角形的外角性质和对顶角相等可知,,
故答案为:40.
3.
【解答】解:,
,
平分,
,
,
,
,
,
平分,
,
,
,
,,,
,
.
故答案为:.
4.【解答】解:为等腰三角形时,
当点在边上时,,
,此时(秒;
当点在边上时.
①如图1,,
作边上的高,
.
,
在中,根据勾股定理得,,
,
,
(秒
②,
,,
(秒;
③,
点在的垂直平分线与的交点处,即在的中点,
此时,
(秒;
综上可知,当秒或5.4秒或6秒或6.5秒时,为等腰三角形.
故答案为:3秒或5.4秒或6秒或6.5秒.
5.
【解答】解:,
设,则,
,
,
,
,
,
故答案为:45.
6.
【解答】解:由题意知,要求“被一条直线分成两个小等腰三角形”,
①中分成的两个等腰三角形的角的度数分别为:,,和,,,能;
②不能;
③显然原等腰直角三角形的斜边上的高把它还分为了两个小等腰直角三角形,能;
④中的为,,和,,,能.
故答案为:②
三、解答题
1.
【解答】解:(1)是等边三角形,
,
,
,,
,
是等边三角形,
的度数为;
(2)证明:点是线段的中点,
由(1)知:是等边三角形,
于点,
,
.
2.
【解答】解:,
(等边对等角),
于,
,
,
(等角的余角相等),
(对顶角相等),
,
,
是等腰三角形.
3.
【解答】解:(1),,
是等边三角形,
,
,
,
.
(2),
是等腰三角形
,
,
为等腰三角形.
,
是等腰三角形.
4.
【解答】(1)证明:,
,
,
是的平分线.
(2)解:,
,
,
,
,,
,
.
5.
【解答】(1)证明:是等边三角形,是中线,
.
(等腰三角形三线合一).
又,
.
又,
.
.
(等角对等边);
(2),
,
,
,
,
,
的周长.
6.
【解答】解:(1),
,
,
,
,
;
(2),,
,
,
,
,
,
,
,
在与中,,
,
,
,
,
,
,
.
故答案为:5.
一、选择题
1.若等腰三角形的两边长分别为2和5,则它的周长为
A.9
B.7
C.12
D.9或12
2.三角形三个内角的比是,则是
A.等腰三角形
B.等腰直角三角形
C.等边三角形
D.不能确定
3.已知:在中,,如要判定是等边三角形,还需添加一个条件.现有下面三种说法:
①如果添加条件“”,那么是等边三角形;
②如果添加条件“”,那么是等边三角形;
③如果添加条件“边、上的高相等”,那么是等边三角形.
上述说法中,正确的有
A.3个
B.2个
C.1个
D.0个
4.上午8时,一条船从海岛出发,以
(海里时,
的速度向正北航行,10时到达海岛处,从、望灯塔,测得,.则从海岛到灯塔的距离为
A.
B.
C.
D.
5.如图,中,,是的平分线,过作交于,若的边长为,则的周长是
A.
B.
C.
D.
6.等腰三角形周长为18,其中一边长为4,则其它两边长分别为
A.4,10
B.7,7
C.4,10或7,7
D.无法确定
7.如图在网格中,已知点、是两格点,若点也是格点,且使为等腰三角形,则点个数是
A.6
B.7
C.8
D.9
二、填空题
1.下面是由同一型号的黑白两种颜色的等边三角形瓷砖按一定规律铺设的图形,仔细观察图形可知:
第1个图形中有1块黑色的瓷砖,可表示为;
第2个图形中有3块黑色的瓷砖,可表示为;
第3个图形中有6块黑色的瓷砖,可表示为;
则第个图形中有 块黑色的瓷砖为正整数).
2.如图,直线,的顶点在直线上,边与直线相交于点.若是等边三角形,,则 .
3.如图,中,平分,平分的外角,经过点与、分别交于点、,并且.则、、之间的数量关系是 .
4.在中,,,.动点从点开始按的路径绕的边运动一周,速度为每秒,运动的时间为秒.则为等腰三角形时的值是 .
5.如图,中,,点在边上,点在边上,,,则的大小为 .
6.如图,下列4个三角形中,均有,则经过三角形的一个顶点的一条直线不能够将这个三角形分成两个小等腰三角形的是 (填序号).
三、解答题
1.如图,是等边三角形,,分别交和于点、.点是线段的中点,连接并延长交于点.
(1)求的度数.
(2)求证:.
2.已知:如图,,是上一点,于点,的延长线交的延长线于点.求证:是等腰三角形.
3.如图所示,在中,,,于点,,交于点,点在的延长线上,且.
(1)求和的度数;
(2)写出图中的等腰三角形(写出3个即可).
4.如图,在中,点是的中点,点是延长线上一点,连接
,交于点,连接,
(1)求证:平分;
(2)若,,求的度数.
5.如图,是等边三角形,是中线,延长至,,
(1)求证:.
(2)在图中过作交于,若,求的周长.
6.如图,已知在四边形中,,,点、点分别在边、上,且,.
(1)求证:;
(2)当时, .
参考答案
一、选择题
1.
【解答】解:(1)若2为腰长,5为底边长,
由于,则三角形不存在;
(2)若5为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为.
故选:.
2.
【解答】解:,,
,.
则该三角形的等腰直角三角形.
故选:.
3.
【解答】解:①若添加的条件为,由,
利用有一个角为的等腰三角形为等边三角形可得出为等边三角形;
②若添加条件为,
又,
,
,
则为等边三角形;
③若添加的条件为边、上的高相等,如图所示:
已知:,,,且,
求证:为等边三角形.
证明:,,
,
在和中,
,
,
,
,
,即为等边三角形,
综上,正确的说法有3个.
故选:.
4.
【解答】解:,,
.
,
,
上午8时,一条船从海岛出发,以
的速度向正北航行.10时到达海岛处,
.
故选:.
5.
【解答】解:是的平分线,是等边三角形,
,
,
,
,
的边长为,
的周长为,
,
解得的周长.
故选:.
6.
【解答】解:当腰为4时,另一腰也为4,则底为,
,
这样的三边不能构成三角形.
当底为4时,腰为,
,
以4,7,7为边能构成三角形
其它两边长分别为7,7.
故选:.
7.
【解答】解:如图:
①以为等腰底边时,符合条件的点有4个:分别为:,,,;
②以为等腰其中的一条腰时,符合条件的点有4个:分别为:,,,.
故选:.
二、填空题
1.
【解答】解:第个图形有:为正整数),
故答案为:.
2.
【解答】解:是等边三角形,
,
,
,
由三角形的外角性质和对顶角相等可知,,
故答案为:40.
3.
【解答】解:,
,
平分,
,
,
,
,
,
平分,
,
,
,
,,,
,
.
故答案为:.
4.【解答】解:为等腰三角形时,
当点在边上时,,
,此时(秒;
当点在边上时.
①如图1,,
作边上的高,
.
,
在中,根据勾股定理得,,
,
,
(秒
②,
,,
(秒;
③,
点在的垂直平分线与的交点处,即在的中点,
此时,
(秒;
综上可知,当秒或5.4秒或6秒或6.5秒时,为等腰三角形.
故答案为:3秒或5.4秒或6秒或6.5秒.
5.
【解答】解:,
设,则,
,
,
,
,
,
故答案为:45.
6.
【解答】解:由题意知,要求“被一条直线分成两个小等腰三角形”,
①中分成的两个等腰三角形的角的度数分别为:,,和,,,能;
②不能;
③显然原等腰直角三角形的斜边上的高把它还分为了两个小等腰直角三角形,能;
④中的为,,和,,,能.
故答案为:②
三、解答题
1.
【解答】解:(1)是等边三角形,
,
,
,,
,
是等边三角形,
的度数为;
(2)证明:点是线段的中点,
由(1)知:是等边三角形,
于点,
,
.
2.
【解答】解:,
(等边对等角),
于,
,
,
(等角的余角相等),
(对顶角相等),
,
,
是等腰三角形.
3.
【解答】解:(1),,
是等边三角形,
,
,
,
.
(2),
是等腰三角形
,
,
为等腰三角形.
,
是等腰三角形.
4.
【解答】(1)证明:,
,
,
是的平分线.
(2)解:,
,
,
,
,,
,
.
5.
【解答】(1)证明:是等边三角形,是中线,
.
(等腰三角形三线合一).
又,
.
又,
.
.
(等角对等边);
(2),
,
,
,
,
,
的周长.
6.
【解答】解:(1),
,
,
,
,
;
(2),,
,
,
,
,
,
,
,
在与中,,
,
,
,
,
,
,
.
故答案为:5.
