11.1 与三角形有关的线段同步练习卷 2021-2022学年人教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 11.1 与三角形有关的线段同步练习卷 2021-2022学年人教版八年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 246.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 21:49:25 | ||
图片预览


文档简介
11.1
与三角形有关的线段
一、选择题
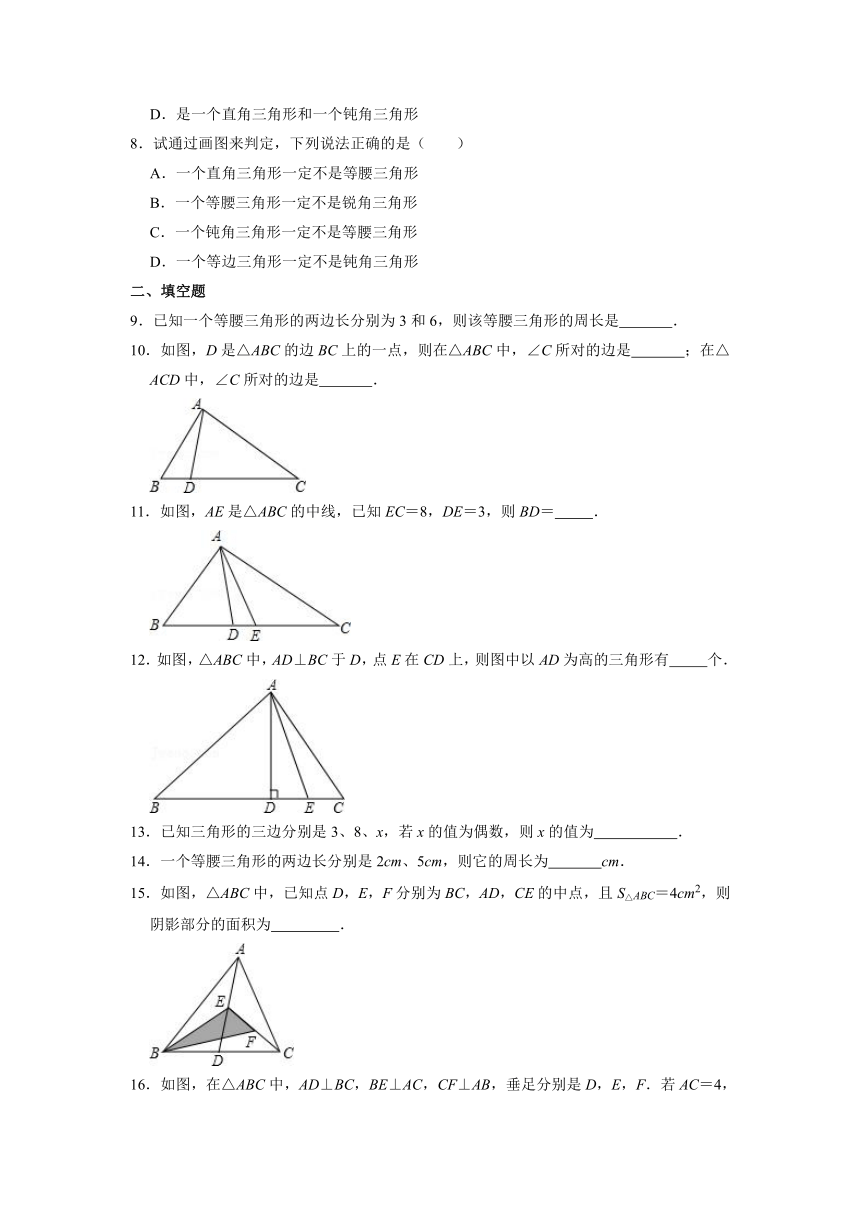
1.如图所示,在△ABC中,D,E,F是BC边上的三点,且∠1=∠2=∠3=∠4,AE是哪个三角形的角平分线( )
A.△ABE
B.△ADF
C.△ABC
D.△ABC,△ADF
2.如图,以AB为边的三角形共有( )个.
A.5
B.4
C.3
D.2
3.下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
4.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A.7
B.8
C.9
D.10
5.四根长度分别为4cm、5cm、9cm、13cm的木条,以其中三根的长为边长,制作成一个三角形框架,那么这个框架的周长可能是( )
A.18cm
B.26cm
C.27cm
D.28cm
6.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添加木条( )
A.1根
B.2根
C.3根
D.4根
7.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
8.试通过画图来判定,下列说法正确的是( )
A.一个直角三角形一定不是等腰三角形
B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形
D.一个等边三角形一定不是钝角三角形
二、填空题
9.已知一个等腰三角形的两边长分别为3和6,则该等腰三角形的周长是
.
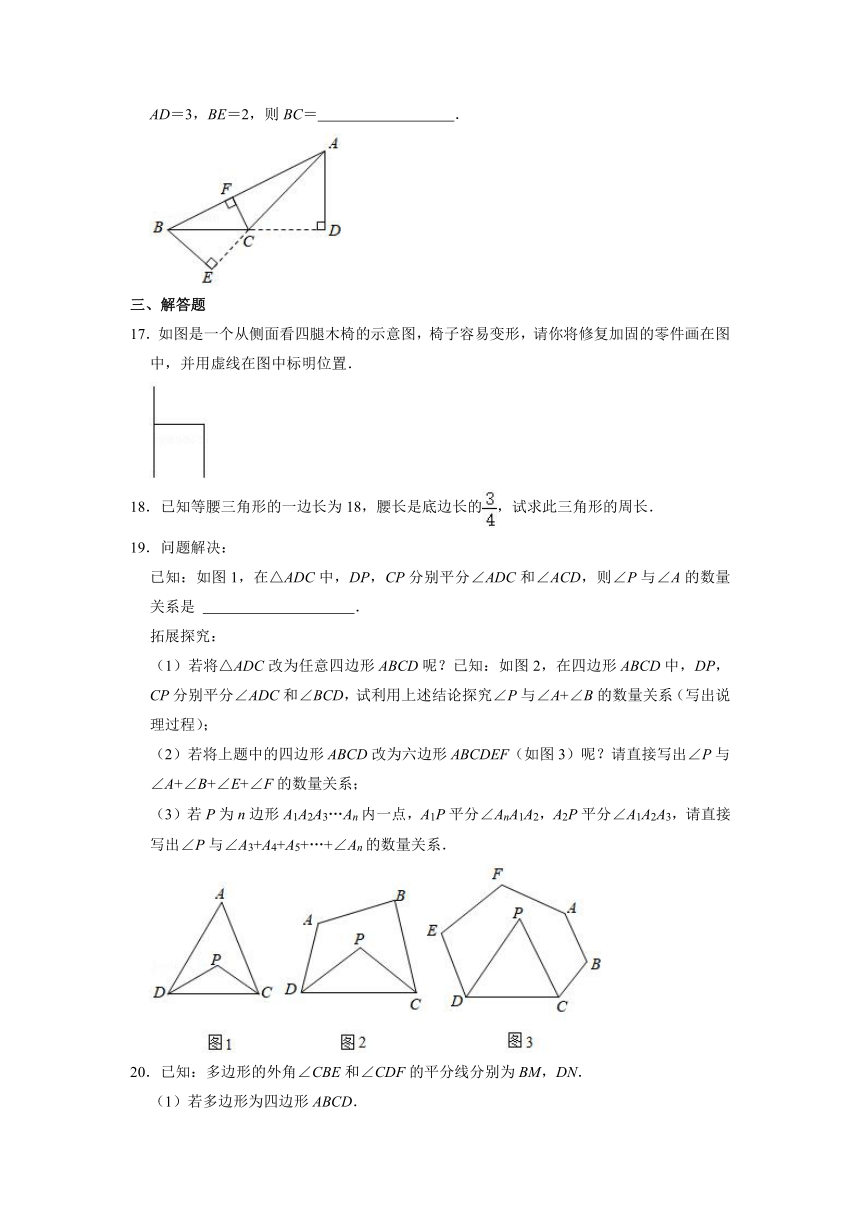
10.如图,D是△ABC的边BC上的一点,则在△ABC中,∠C所对的边是
;在△ACD中,∠C所对的边是
.
11.如图,AE是△ABC的中线,已知EC=8,DE=3,则BD=
.
12.如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有
个.
13.已知三角形的三边分别是3、8、x,若x的值为偶数,则x的值为
.
14.一个等腰三角形的两边长分别是2cm、5cm,则它的周长为
cm.
15.如图,△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为
.
16.如图,在△ABC中,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别是D,E,F.若AC=4,AD=3,BE=2,则BC=
.
三、解答题
17.如图是一个从侧面看四腿木椅的示意图,椅子容易变形,请你将修复加固的零件画在图中,并用虚线在图中标明位置.
18.已知等腰三角形的一边长为18,腰长是底边长的,试求此三角形的周长.
19.问题解决:
已知:如图1,在△ADC中,DP,CP分别平分∠ADC和∠ACD,则∠P与∠A的数量关系是
.
拓展探究:
(1)若将△ADC改为任意四边形ABCD呢?已知:如图2,在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系(写出说理过程);
(2)若将上题中的四边形ABCD改为六边形ABCDEF(如图3)呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系;
(3)若P为n边形A1A2A3…An内一点,A1P平分∠AnA1A2,A2P平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…+∠An的数量关系.
20.已知:多边形的外角∠CBE和∠CDF的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
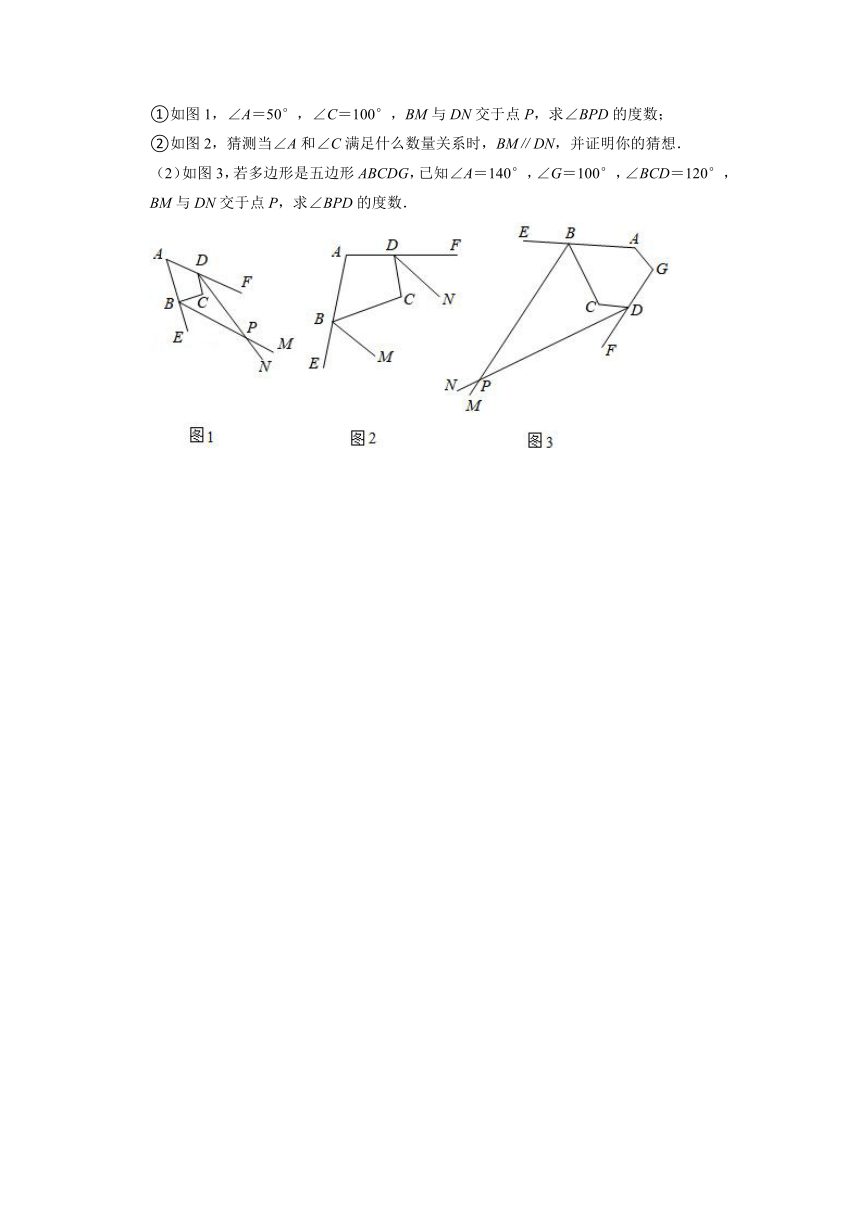
①如图1,∠A=50°,∠C=100°,BM与DN交于点P,求∠BPD的度数;
②如图2,猜测当∠A和∠C满足什么数量关系时,BM∥DN,并证明你的猜想.
(2)如图3,若多边形是五边形ABCDG,已知∠A=140°,∠G=100°,∠BCD=120°,BM与DN交于点P,求∠BPD的度数.
参考答案与试题解析
一、选择题
1.如图所示,在△ABC中,D,E,F是BC边上的三点,且∠1=∠2=∠3=∠4,AE是哪个三角形的角平分线( )
A.△ABE
B.△ADF
C.△ABC
D.△ABC,△ADF
【分析】根据三角形的角平分线的定义得出.
【解答】解:∵∠2=∠3,
∴AE是△ADF的角平分线;
∵∠1=∠2=∠3=∠4,
∴∠1+∠2=∠3+∠4,即∠BAE=∠CAE,
∴AE是△ABC的角平分线.
故选:D.
2.如图,以AB为边的三角形共有( )个.
A.5
B.4
C.3
D.2
【分析】根据三角形的组成得出以AB为边的三角形;
【解答】解:以AB为边的三角形共有3个,它们是△ABC,△ABE,△ABD.
故选:C.
3.下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
【分析】根据三角形三边关系定理判断即可.
【解答】解:∵5+6<12,
∴三角形三边长为5,6,12不可能成为一个三角形,
故选:C.
4.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A.7
B.8
C.9
D.10
【分析】根据三角形的三边关系“第三边大于两边之差,而小于两边之和”,求得第三边的取值范围;再根据第三边是整数,从而求得周长.
【解答】解:设第三边为x,
根据三角形的三边关系,得:4﹣1<x<4+1,
即3<x<5,
∵x为整数,
∴x的值为4.
三角形的周长为1+4+4=9.
故选:C.
5.四根长度分别为4cm、5cm、9cm、13cm的木条,以其中三根的长为边长,制作成一个三角形框架,那么这个框架的周长可能是( )
A.18cm
B.26cm
C.27cm
D.28cm
【分析】首先写出所有的组合情况,再进一步根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:其中的任意三条组合有4cm、5cm、9cm;4cm、5cm、13cm;4cm、9cm、13cm;5cm、9cm、13cm共四种情况,
根据三角形的三边关系,则只有5cm、9cm、13cm符合,故周长是27cm.
故选:C.
6.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添加木条( )
A.1根
B.2根
C.3根
D.4根
【分析】根据三角形的稳定性,只要使六边形框架ABCDEF变成三角形的组合体即可.
【解答】解:根据三角形的稳定性,得
如图:从图中可以看出,要使框架稳固且不活动,至少还需要添3根木条,
故选:C.
7.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
【分析】分三种情况讨论,即可得到这两个三角形不可能都是锐角三角形.
【解答】解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:C.
8.试通过画图来判定,下列说法正确的是( )
A.一个直角三角形一定不是等腰三角形
B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形
D.一个等边三角形一定不是钝角三角形
【分析】根据三角形的分类方法进行分析判断.三角形按角分为锐角三角形、直角三角形和钝角三角形;三角形按边分为不等边三角形和等腰三角形(等边三角形).
【解答】解:A、如等腰直角三角形,既是直角三角形,也是等腰三角形,故该选项错误;
B、如等边三角形,既是等腰三角形,也是锐角三角形,故该选项错误;
C、如顶角是120°的等腰三角形,是钝角三角形,也是等腰三角形,故该选项错误;
D、一个等边三角形的三个角都是60°.故该选项正确.
故选:D.
二、填空题
9.已知一个等腰三角形的两边长分别为3和6,则该等腰三角形的周长是 15 .
【分析】分腰为3和腰为6两种情况考虑,先根据三角形的三边关系确定三角形是否存在,再根据三角形的周长公式求值即可.
【解答】解:当腰为3时,3+3=6,
∴3、3、6不能组成三角形;
当腰为6时,3+6=9>6,
∴3、6、6能组成三角形,
该三角形的周长=3+6+6=15.
故答案为:15.
10.如图,D是△ABC的边BC上的一点,则在△ABC中,∠C所对的边是 AB ;在△ACD中,∠C所对的边是 AD .
【分析】根据三角形的边和角有关概念解答即可.
【解答】解:在△ABC中,∠C所对的边是AB;在△ACD中,∠C所对的边是AD,
故答案为:AB;AD.
11.如图,AE是△ABC的中线,已知EC=8,DE=3,则BD= 5 .
【分析】根据三角形中线的定义可得BE=EC=8,再根据BD=BE﹣DE即可求解.
【解答】解:∵AE是△ABC的中线,EC=8,
∴BE=EC=8,
∵DE=3,
∴BD=BE﹣DE=8﹣3=5.
故答案为:5
12.如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有 6 个.
【分析】由于AD⊥BC于D,图中共有6个三角形,它们都有一边在直线CB上,由此即可确定以AD为高的三角形的个数.
【解答】解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6.
13.已知三角形的三边分别是3、8、x,若x的值为偶数,则x的值为 6、8或10 .
【分析】根据三角形的三边关系“第三边应大于两边之差,而小于两边之和”,求得第三边的取值范围;再根据第三边是偶数这一条件,求得第三边的值.
【解答】解:根据三角形的三边关系,得:
第三边x的取值范围:5<x<11,
又∵第三边的长是偶数,
则第三边的长为6、8或10.
故答案为6、8或10.
14.一个等腰三角形的两边长分别是2cm、5cm,则它的周长为 12 cm.
【分析】本题没有明确说明已知的边长那一条是腰长,所以需要分两种情况讨论.
【解答】解:分两种情况讨论
①腰长为5时,三边为5、5、2,满足三角形的性质,周长=5+5+2=12cm;
②腰长为2cm时,三边为5、2、2,
∵2+2=4<5,
∴不满足构成三角形.
∴周长为12cm.
故答案为:12.
15.如图,△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为 1cm2 .
【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.
【解答】解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×4=2cm2,
∴S△BCE=S△ABC=×4=2cm2,
∵点F是CE的中点,
∴S△BEF=S△BCE=×2=1cm2.
故答案为:1cm2.
16.如图,在△ABC中,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别是D,E,F.若AC=4,AD=3,BE=2,则BC= .
【分析】根据三角形面积公式得到?BC?AD=?AC?BE,然后把AC=4,AD=3,BE=2代入可求出BC的长.
【解答】解:∵AD⊥BC,BE⊥AC,
∴S△ABC=?BC?AD=?AC?BE,
∴BC===.
故答案为.
三、解答题
17.如图是一个从侧面看四腿木椅的示意图,椅子容易变形,请你将修复加固的零件画在图中,并用虚线在图中标明位置.
【分析】利用三角形稳定性即可解题.
【解答】解:因为四边形不具有稳定性,
所以椅子会变形.利用三角形的稳定性,
可用三角形角铁对椅子修复加固,如图:
18.已知等腰三角形的一边长为18,腰长是底边长的,试求此三角形的周长.
【分析】因为等腰三角形的一边长为18,但没有明确是底边还是腰,所以有两种情况,需要分类讨论,还要利用三边关系验证能否组成三角形.
【解答】解:∵等腰三角形一边长为18cm,且腰长是底边长的,
①如果腰长为18cm,则底边为24cm,
等腰三角形的三边为18、18、24,能构成三角形,
∴C△=18+18+24=60cm;
②如果底长为18cm,则腰长为13.5cm,
等腰三角形的三边为18、13.5、13.5,能构成三角形,
∴C△=13.5+13.5+18=45cm.
19.问题解决:
已知:如图1,在△ADC中,DP,CP分别平分∠ADC和∠ACD,则∠P与∠A的数量关系是
∠P=90°+∠A .
拓展探究:
(1)若将△ADC改为任意四边形ABCD呢?已知:如图2,在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系(写出说理过程);
(2)若将上题中的四边形ABCD改为六边形ABCDEF(如图3)呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系;
(3)若P为n边形A1A2A3…An内一点,A1P平分∠AnA1A2,A2P平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…+∠An的数量关系.
【分析】问题解决:根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;
(1)根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据四边形的内角和定理表示出∠ADC+∠BCD解答即可;
(2)根据六边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;
(3)根据n边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可.
【解答】解:问题解决:∠P=90°+∠A.
故答案为:∠P=90°+∠A;
拓展探究:
(1)∵DP,CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD.
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠BCD
=180°﹣(∠ADC+∠BCD)
=180°﹣(360°﹣∠A﹣∠B)
=(∠A+∠B).
(2)∠P=(∠A+∠B+∠E+∠F)﹣180°.
(3)∠P=(∠A3+∠A4+∠A5+…+∠An)﹣(n﹣4)×90°.
20.已知:多边形的外角∠CBE和∠CDF的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
①如图1,∠A=50°,∠C=100°,BM与DN交于点P,求∠BPD的度数;
②如图2,猜测当∠A和∠C满足什么数量关系时,BM∥DN,并证明你的猜想.
(2)如图3,若多边形是五边形ABCDG,已知∠A=140°,∠G=100°,∠BCD=120°,BM与DN交于点P,求∠BPD的度数.
【分析】(1)①由∠A=50°,∠C=100°,可推出∠CBE+∠CDF=150°,由角平分线的性质可得∠PBC+∠PDC=75°,再由∠BPD=360°﹣∠A﹣(∠ABC+∠ADC)﹣(∠PBC+∠PDC)计算,即可得出结果;
②连接BD.由BM∥DN,可得∠BDN+∠DBM=180°,进而可得∠FDN+∠ADB+∠ABD+∠MBE=180°,(360°﹣360°+∠A+∠C)+(180°﹣∠A)=180°,计算即可得出∠A=∠C;
(2)延长DC交BP于点Q.由∠A=140°,∠G=100°,∠BCD=120°及五边形内角和定理可得∠ABC+∠CDG=180°,进而得∠CBE+∠CDF=360°﹣180°=180°,由BP平分∠CBE,DP平分∠CDF,可得∠CBP+∠CDP=(∠CBE+∠CDF)=90°,进一步可推出∠BPD=∠BCD﹣(∠CBP+∠QDP)=120°﹣90°=30°.
【解答】解:(1)①∵∠A=50°,∠C=100°,
∴在四边形ABCD中,
∠ABC+∠ADC=360°﹣∠A﹣∠C=210°,
∴∠CBE+∠CDF=150°.
∵外角∠CBE和∠CDF的平分线分别为BM,DN,
∴∠PBC+∠PDC=∠CBE+∠CDF=(∠CBE+∠CDF)=×150°=75°,
∴∠BPD=360°﹣∠A﹣(∠ABC+∠ADC)﹣(∠PBC+∠PDC)=360°﹣50°﹣210°﹣75°=25°;
②当∠A=∠C时,BM∥DN.
证明:如图,连接BD.
∵BM∥DN,
∴∠BDN+∠DBM=180°,
∴∠FDN+∠ADB+∠ABD+∠MBE=360°﹣180°=180°,
即(∠FDC+∠CBE)+(∠ADB+∠ABD)=180°,
∴(360°﹣∠ADC﹣∠CBA)+(180°﹣∠A)=180°,
∴(360°﹣360°+∠A+∠C)+(180°﹣∠A)=180°,
∴∠A=∠C.
(2)如图,延长DC交BP于点Q.
∵∠A=140°,∠G=100°,∠BCD=120°,
∠A+∠ABC+∠BCD+∠CDG+∠G=540°,
∴∠ABC+∠CDG=180°,
∴∠CBE+∠CDF=360°﹣180°=180°,
∵BP平分∠CBE,DP平分∠CDF,
∴∠CBP+∠CDP=(∠CBE+∠CDF)=90°,
∵∠BCD=∠CBP+∠CQB,∠CQB=∠QDP+∠BPD,
∴∠BCD=∠CBP+∠QDP+∠BPD,
∴∠BPD=∠BCD﹣(∠CBP+∠QDP)=120°﹣90°=30°.
与三角形有关的线段
一、选择题
1.如图所示,在△ABC中,D,E,F是BC边上的三点,且∠1=∠2=∠3=∠4,AE是哪个三角形的角平分线( )
A.△ABE
B.△ADF
C.△ABC
D.△ABC,△ADF
2.如图,以AB为边的三角形共有( )个.
A.5
B.4
C.3
D.2
3.下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
4.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A.7
B.8
C.9
D.10
5.四根长度分别为4cm、5cm、9cm、13cm的木条,以其中三根的长为边长,制作成一个三角形框架,那么这个框架的周长可能是( )
A.18cm
B.26cm
C.27cm
D.28cm
6.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添加木条( )
A.1根
B.2根
C.3根
D.4根
7.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
8.试通过画图来判定,下列说法正确的是( )
A.一个直角三角形一定不是等腰三角形
B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形
D.一个等边三角形一定不是钝角三角形
二、填空题
9.已知一个等腰三角形的两边长分别为3和6,则该等腰三角形的周长是
.
10.如图,D是△ABC的边BC上的一点,则在△ABC中,∠C所对的边是
;在△ACD中,∠C所对的边是
.
11.如图,AE是△ABC的中线,已知EC=8,DE=3,则BD=
.
12.如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有
个.
13.已知三角形的三边分别是3、8、x,若x的值为偶数,则x的值为
.
14.一个等腰三角形的两边长分别是2cm、5cm,则它的周长为
cm.
15.如图,△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为
.
16.如图,在△ABC中,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别是D,E,F.若AC=4,AD=3,BE=2,则BC=
.
三、解答题
17.如图是一个从侧面看四腿木椅的示意图,椅子容易变形,请你将修复加固的零件画在图中,并用虚线在图中标明位置.
18.已知等腰三角形的一边长为18,腰长是底边长的,试求此三角形的周长.
19.问题解决:
已知:如图1,在△ADC中,DP,CP分别平分∠ADC和∠ACD,则∠P与∠A的数量关系是
.
拓展探究:
(1)若将△ADC改为任意四边形ABCD呢?已知:如图2,在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系(写出说理过程);
(2)若将上题中的四边形ABCD改为六边形ABCDEF(如图3)呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系;
(3)若P为n边形A1A2A3…An内一点,A1P平分∠AnA1A2,A2P平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…+∠An的数量关系.
20.已知:多边形的外角∠CBE和∠CDF的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
①如图1,∠A=50°,∠C=100°,BM与DN交于点P,求∠BPD的度数;
②如图2,猜测当∠A和∠C满足什么数量关系时,BM∥DN,并证明你的猜想.
(2)如图3,若多边形是五边形ABCDG,已知∠A=140°,∠G=100°,∠BCD=120°,BM与DN交于点P,求∠BPD的度数.
参考答案与试题解析
一、选择题
1.如图所示,在△ABC中,D,E,F是BC边上的三点,且∠1=∠2=∠3=∠4,AE是哪个三角形的角平分线( )
A.△ABE
B.△ADF
C.△ABC
D.△ABC,△ADF
【分析】根据三角形的角平分线的定义得出.
【解答】解:∵∠2=∠3,
∴AE是△ADF的角平分线;
∵∠1=∠2=∠3=∠4,
∴∠1+∠2=∠3+∠4,即∠BAE=∠CAE,
∴AE是△ABC的角平分线.
故选:D.
2.如图,以AB为边的三角形共有( )个.
A.5
B.4
C.3
D.2
【分析】根据三角形的组成得出以AB为边的三角形;
【解答】解:以AB为边的三角形共有3个,它们是△ABC,△ABE,△ABD.
故选:C.
3.下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
【分析】根据三角形三边关系定理判断即可.
【解答】解:∵5+6<12,
∴三角形三边长为5,6,12不可能成为一个三角形,
故选:C.
4.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A.7
B.8
C.9
D.10
【分析】根据三角形的三边关系“第三边大于两边之差,而小于两边之和”,求得第三边的取值范围;再根据第三边是整数,从而求得周长.
【解答】解:设第三边为x,
根据三角形的三边关系,得:4﹣1<x<4+1,
即3<x<5,
∵x为整数,
∴x的值为4.
三角形的周长为1+4+4=9.
故选:C.
5.四根长度分别为4cm、5cm、9cm、13cm的木条,以其中三根的长为边长,制作成一个三角形框架,那么这个框架的周长可能是( )
A.18cm
B.26cm
C.27cm
D.28cm
【分析】首先写出所有的组合情况,再进一步根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:其中的任意三条组合有4cm、5cm、9cm;4cm、5cm、13cm;4cm、9cm、13cm;5cm、9cm、13cm共四种情况,
根据三角形的三边关系,则只有5cm、9cm、13cm符合,故周长是27cm.
故选:C.
6.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添加木条( )
A.1根
B.2根
C.3根
D.4根
【分析】根据三角形的稳定性,只要使六边形框架ABCDEF变成三角形的组合体即可.
【解答】解:根据三角形的稳定性,得
如图:从图中可以看出,要使框架稳固且不活动,至少还需要添3根木条,
故选:C.
7.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
【分析】分三种情况讨论,即可得到这两个三角形不可能都是锐角三角形.
【解答】解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:C.
8.试通过画图来判定,下列说法正确的是( )
A.一个直角三角形一定不是等腰三角形
B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形
D.一个等边三角形一定不是钝角三角形
【分析】根据三角形的分类方法进行分析判断.三角形按角分为锐角三角形、直角三角形和钝角三角形;三角形按边分为不等边三角形和等腰三角形(等边三角形).
【解答】解:A、如等腰直角三角形,既是直角三角形,也是等腰三角形,故该选项错误;
B、如等边三角形,既是等腰三角形,也是锐角三角形,故该选项错误;
C、如顶角是120°的等腰三角形,是钝角三角形,也是等腰三角形,故该选项错误;
D、一个等边三角形的三个角都是60°.故该选项正确.
故选:D.
二、填空题
9.已知一个等腰三角形的两边长分别为3和6,则该等腰三角形的周长是 15 .
【分析】分腰为3和腰为6两种情况考虑,先根据三角形的三边关系确定三角形是否存在,再根据三角形的周长公式求值即可.
【解答】解:当腰为3时,3+3=6,
∴3、3、6不能组成三角形;
当腰为6时,3+6=9>6,
∴3、6、6能组成三角形,
该三角形的周长=3+6+6=15.
故答案为:15.
10.如图,D是△ABC的边BC上的一点,则在△ABC中,∠C所对的边是 AB ;在△ACD中,∠C所对的边是 AD .
【分析】根据三角形的边和角有关概念解答即可.
【解答】解:在△ABC中,∠C所对的边是AB;在△ACD中,∠C所对的边是AD,
故答案为:AB;AD.
11.如图,AE是△ABC的中线,已知EC=8,DE=3,则BD= 5 .
【分析】根据三角形中线的定义可得BE=EC=8,再根据BD=BE﹣DE即可求解.
【解答】解:∵AE是△ABC的中线,EC=8,
∴BE=EC=8,
∵DE=3,
∴BD=BE﹣DE=8﹣3=5.
故答案为:5
12.如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有 6 个.
【分析】由于AD⊥BC于D,图中共有6个三角形,它们都有一边在直线CB上,由此即可确定以AD为高的三角形的个数.
【解答】解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6.
13.已知三角形的三边分别是3、8、x,若x的值为偶数,则x的值为 6、8或10 .
【分析】根据三角形的三边关系“第三边应大于两边之差,而小于两边之和”,求得第三边的取值范围;再根据第三边是偶数这一条件,求得第三边的值.
【解答】解:根据三角形的三边关系,得:
第三边x的取值范围:5<x<11,
又∵第三边的长是偶数,
则第三边的长为6、8或10.
故答案为6、8或10.
14.一个等腰三角形的两边长分别是2cm、5cm,则它的周长为 12 cm.
【分析】本题没有明确说明已知的边长那一条是腰长,所以需要分两种情况讨论.
【解答】解:分两种情况讨论
①腰长为5时,三边为5、5、2,满足三角形的性质,周长=5+5+2=12cm;
②腰长为2cm时,三边为5、2、2,
∵2+2=4<5,
∴不满足构成三角形.
∴周长为12cm.
故答案为:12.
15.如图,△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为 1cm2 .
【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.
【解答】解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×4=2cm2,
∴S△BCE=S△ABC=×4=2cm2,
∵点F是CE的中点,
∴S△BEF=S△BCE=×2=1cm2.
故答案为:1cm2.
16.如图,在△ABC中,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别是D,E,F.若AC=4,AD=3,BE=2,则BC= .
【分析】根据三角形面积公式得到?BC?AD=?AC?BE,然后把AC=4,AD=3,BE=2代入可求出BC的长.
【解答】解:∵AD⊥BC,BE⊥AC,
∴S△ABC=?BC?AD=?AC?BE,
∴BC===.
故答案为.
三、解答题
17.如图是一个从侧面看四腿木椅的示意图,椅子容易变形,请你将修复加固的零件画在图中,并用虚线在图中标明位置.
【分析】利用三角形稳定性即可解题.
【解答】解:因为四边形不具有稳定性,
所以椅子会变形.利用三角形的稳定性,
可用三角形角铁对椅子修复加固,如图:
18.已知等腰三角形的一边长为18,腰长是底边长的,试求此三角形的周长.
【分析】因为等腰三角形的一边长为18,但没有明确是底边还是腰,所以有两种情况,需要分类讨论,还要利用三边关系验证能否组成三角形.
【解答】解:∵等腰三角形一边长为18cm,且腰长是底边长的,
①如果腰长为18cm,则底边为24cm,
等腰三角形的三边为18、18、24,能构成三角形,
∴C△=18+18+24=60cm;
②如果底长为18cm,则腰长为13.5cm,
等腰三角形的三边为18、13.5、13.5,能构成三角形,
∴C△=13.5+13.5+18=45cm.
19.问题解决:
已知:如图1,在△ADC中,DP,CP分别平分∠ADC和∠ACD,则∠P与∠A的数量关系是
∠P=90°+∠A .
拓展探究:
(1)若将△ADC改为任意四边形ABCD呢?已知:如图2,在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系(写出说理过程);
(2)若将上题中的四边形ABCD改为六边形ABCDEF(如图3)呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系;
(3)若P为n边形A1A2A3…An内一点,A1P平分∠AnA1A2,A2P平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…+∠An的数量关系.
【分析】问题解决:根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;
(1)根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据四边形的内角和定理表示出∠ADC+∠BCD解答即可;
(2)根据六边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;
(3)根据n边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可.
【解答】解:问题解决:∠P=90°+∠A.
故答案为:∠P=90°+∠A;
拓展探究:
(1)∵DP,CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD.
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠BCD
=180°﹣(∠ADC+∠BCD)
=180°﹣(360°﹣∠A﹣∠B)
=(∠A+∠B).
(2)∠P=(∠A+∠B+∠E+∠F)﹣180°.
(3)∠P=(∠A3+∠A4+∠A5+…+∠An)﹣(n﹣4)×90°.
20.已知:多边形的外角∠CBE和∠CDF的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
①如图1,∠A=50°,∠C=100°,BM与DN交于点P,求∠BPD的度数;
②如图2,猜测当∠A和∠C满足什么数量关系时,BM∥DN,并证明你的猜想.
(2)如图3,若多边形是五边形ABCDG,已知∠A=140°,∠G=100°,∠BCD=120°,BM与DN交于点P,求∠BPD的度数.
【分析】(1)①由∠A=50°,∠C=100°,可推出∠CBE+∠CDF=150°,由角平分线的性质可得∠PBC+∠PDC=75°,再由∠BPD=360°﹣∠A﹣(∠ABC+∠ADC)﹣(∠PBC+∠PDC)计算,即可得出结果;
②连接BD.由BM∥DN,可得∠BDN+∠DBM=180°,进而可得∠FDN+∠ADB+∠ABD+∠MBE=180°,(360°﹣360°+∠A+∠C)+(180°﹣∠A)=180°,计算即可得出∠A=∠C;
(2)延长DC交BP于点Q.由∠A=140°,∠G=100°,∠BCD=120°及五边形内角和定理可得∠ABC+∠CDG=180°,进而得∠CBE+∠CDF=360°﹣180°=180°,由BP平分∠CBE,DP平分∠CDF,可得∠CBP+∠CDP=(∠CBE+∠CDF)=90°,进一步可推出∠BPD=∠BCD﹣(∠CBP+∠QDP)=120°﹣90°=30°.
【解答】解:(1)①∵∠A=50°,∠C=100°,
∴在四边形ABCD中,
∠ABC+∠ADC=360°﹣∠A﹣∠C=210°,
∴∠CBE+∠CDF=150°.
∵外角∠CBE和∠CDF的平分线分别为BM,DN,
∴∠PBC+∠PDC=∠CBE+∠CDF=(∠CBE+∠CDF)=×150°=75°,
∴∠BPD=360°﹣∠A﹣(∠ABC+∠ADC)﹣(∠PBC+∠PDC)=360°﹣50°﹣210°﹣75°=25°;
②当∠A=∠C时,BM∥DN.
证明:如图,连接BD.
∵BM∥DN,
∴∠BDN+∠DBM=180°,
∴∠FDN+∠ADB+∠ABD+∠MBE=360°﹣180°=180°,
即(∠FDC+∠CBE)+(∠ADB+∠ABD)=180°,
∴(360°﹣∠ADC﹣∠CBA)+(180°﹣∠A)=180°,
∴(360°﹣360°+∠A+∠C)+(180°﹣∠A)=180°,
∴∠A=∠C.
(2)如图,延长DC交BP于点Q.
∵∠A=140°,∠G=100°,∠BCD=120°,
∠A+∠ABC+∠BCD+∠CDG+∠G=540°,
∴∠ABC+∠CDG=180°,
∴∠CBE+∠CDF=360°﹣180°=180°,
∵BP平分∠CBE,DP平分∠CDF,
∴∠CBP+∠CDP=(∠CBE+∠CDF)=90°,
∵∠BCD=∠CBP+∠CQB,∠CQB=∠QDP+∠BPD,
∴∠BCD=∠CBP+∠QDP+∠BPD,
∴∠BPD=∠BCD﹣(∠CBP+∠QDP)=120°﹣90°=30°.
