冀教五年级上册数学6.5组合图形面积 课件
文档属性
| 名称 | 冀教五年级上册数学6.5组合图形面积 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 10:27:26 | ||
图片预览




文档简介
(共21张PPT)
多边形的面积
第5课时
组合图形面积
课堂导入-新知探究-课堂练习-课堂小结-课堂作业
冀教版
数学
五年级
上册
1.经历尝试计算组合图形面积、交流不同计算方法的过程。
2.能运用学过的面积公式计算组合图形面积,体验算法的多样化。
3.能够探索出计算组合图形面积的有效方法,并试图寻找其他方法,获得运用数学知识解决问题的成功体验。
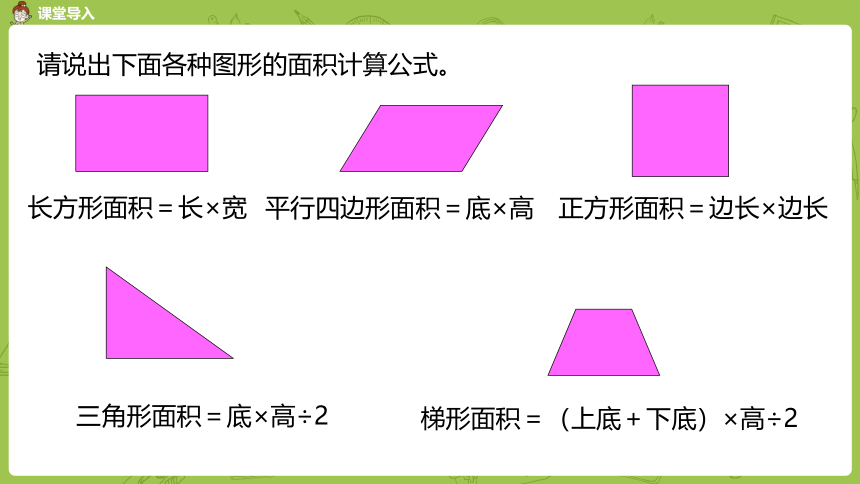
请说出下面各种图形的面积计算公式。
长方形面积=长×宽
平行四边形面积=底×高
梯形面积=(上底+下底)×高÷2
正方形面积=边长×边长
三角形面积=底×高÷2
把你的做法和同学交流一下。
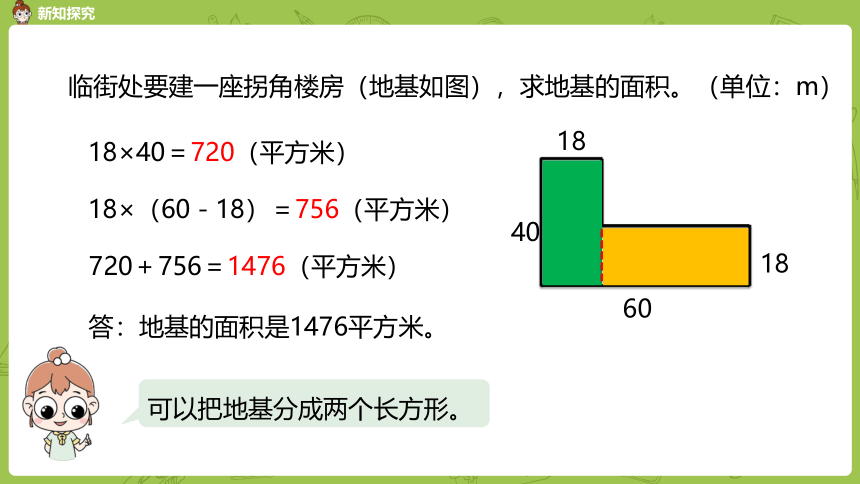
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
18
60
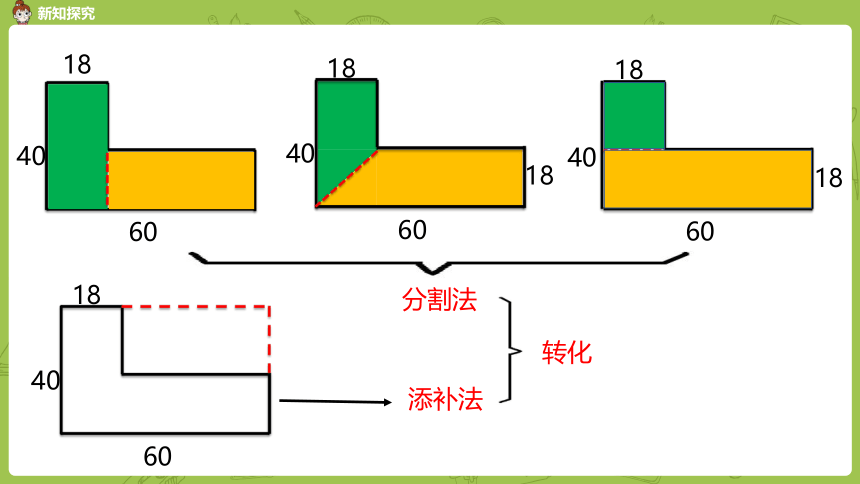
可以把地基分成两个长方形。
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
18
60
18×40=720(平方米)
18×(60-18)=756(平方米)
720+756=1476(平方米)
答:地基的面积是1476平方米。
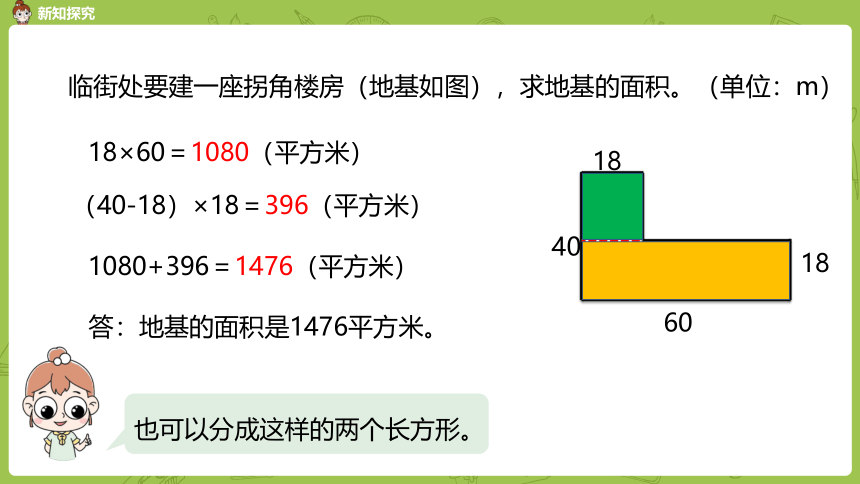
也可以分成这样的两个长方形。
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
60
18
18×60=1080(平方米)
(40-18)×18=396(平方米)
1080+396=1476(平方米)
答:地基的面积是1476平方米。
还可以把地基分成两个梯形。
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
60
(40-18+40)×18÷2=558(平方米)
(60-18+60)×18÷2=918(平方米)
558+918=1476(平方米)
答:地基的面积是1476平方米。
18
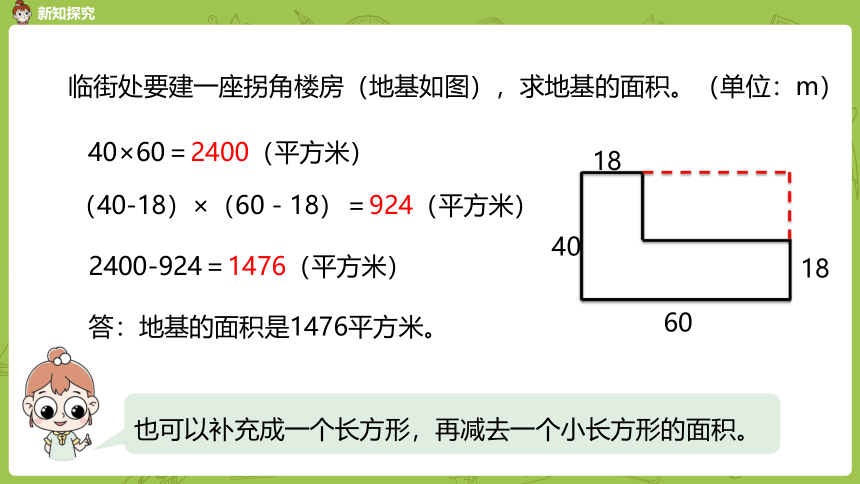
也可以补充成一个长方形,再减去一个小长方形的面积。
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
60
40×60=2400(平方米)
(40-18)×(60-18)=924(平方米)
2400-924=1476(平方米)
答:地基的面积是1476平方米。
18
18
40
60
18
40
60
18
18
40
60
分割法
添补法
转化
18
40
60
18
1
4×1.5÷2+4×2÷2
=6÷2+4×2÷2
=3+4×2÷2
=3+8÷2
=3+4
=7(cm?)
用分割法计算下面图形的面积。(单位:厘米)
1
用分割法计算下面图形的面积。(单位:厘米)
(8+16)×(16-9)÷2=84(平方厘米)
9×16=144(平方厘米)
84+144=228(平方厘米)
1
用分割法计算下面图形的面积。(单位:厘米)
(20-15)×(25-15)÷2=25(平方厘米)
15×25=375(平方厘米)
25+375=400(平方厘米)
2
用添补法计算组合图形的面积。(单位:厘米)
(10+20)×22÷2
=30×22÷2
=660÷2
=330(平方厘米)
8×6÷2
=48÷2
=24(平方厘米)
330-24=306(平方厘米)
2
用添补法计算组合图形的面积。(单位:厘米)
13×20=260(平方厘米)
12×5÷2
=60÷2
=30(平方厘米)
260-30=230(平方厘米)
求组合图形面积的基本方法
1.观察分析组合图形可分割或添补成哪些已经学过的基本图形。
2.找出计算基本图形面积需要的条件。
3.利用合理的方法,先计算出基本图形的面积,再计算出组合图形的面积。
填一填。
1
(1)计算组合图形的面积时,我们先要把它(
)成我们以前学过的(
)。然后分别计算出它们的面积,最后再把结果进行加或减。
(2)求下面图形的面积是(
)
(已知条件如图中所示,单位:cm).
割补
基本图形
9平方厘米
(1)计算组合图形的面积也要用到基本图形的面积公式。(
)
(2)用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。(
)
(3)任何两个三角形都可以拼成一个四边形。
??(?
?)
×
√
√
判断。
2
(1)两个面积相等的正方形拼成一个长方形,拼接前后的面积(???
)。
A.?增大??B.?减少???C.?不变???D.?无法确定
(2)如图中的阴影部分面积是(?
)平方厘米
A.?144?????????????B.?72?????????C.?18????????D.?无法确定
?????????????????????????????????
???????????????????????????????
3
选择。
?C
B
一块菜地(如下图),求它的面积。(单位:m)
4
18×18÷2=162(平方米)
(18+12)×22÷2=330(平方米)
162+330=492(平方米)
答:它的面积是492平方米。
一块稻田,中间有一条水渠通过。
5
(1)实际种水稻的面积是多少平方米?
(48+44)×21÷2=966(平方米)
1.5×21=31.5(平方米)
966-31.5=934.5(平方米)
答:实际种水稻的面积是934.5平方米。
一块稻田,中间有一条水渠通过。
5
(2)如果每平方米稻田产水稻1.2千克,那么这块稻田共产水稻多少千克?
934.5×1.2=1121.4(千克)
答:这块稻田共产水稻1121.4千克。
多边形的面积
第5课时
组合图形面积
课堂导入-新知探究-课堂练习-课堂小结-课堂作业
冀教版
数学
五年级
上册
1.经历尝试计算组合图形面积、交流不同计算方法的过程。
2.能运用学过的面积公式计算组合图形面积,体验算法的多样化。
3.能够探索出计算组合图形面积的有效方法,并试图寻找其他方法,获得运用数学知识解决问题的成功体验。
请说出下面各种图形的面积计算公式。
长方形面积=长×宽
平行四边形面积=底×高
梯形面积=(上底+下底)×高÷2
正方形面积=边长×边长
三角形面积=底×高÷2
把你的做法和同学交流一下。
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
18
60
可以把地基分成两个长方形。
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
18
60
18×40=720(平方米)
18×(60-18)=756(平方米)
720+756=1476(平方米)
答:地基的面积是1476平方米。
也可以分成这样的两个长方形。
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
60
18
18×60=1080(平方米)
(40-18)×18=396(平方米)
1080+396=1476(平方米)
答:地基的面积是1476平方米。
还可以把地基分成两个梯形。
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
60
(40-18+40)×18÷2=558(平方米)
(60-18+60)×18÷2=918(平方米)
558+918=1476(平方米)
答:地基的面积是1476平方米。
18
也可以补充成一个长方形,再减去一个小长方形的面积。
临街处要建一座拐角楼房(地基如图),求地基的面积。(单位:m)
18
40
60
40×60=2400(平方米)
(40-18)×(60-18)=924(平方米)
2400-924=1476(平方米)
答:地基的面积是1476平方米。
18
18
40
60
18
40
60
18
18
40
60
分割法
添补法
转化
18
40
60
18
1
4×1.5÷2+4×2÷2
=6÷2+4×2÷2
=3+4×2÷2
=3+8÷2
=3+4
=7(cm?)
用分割法计算下面图形的面积。(单位:厘米)
1
用分割法计算下面图形的面积。(单位:厘米)
(8+16)×(16-9)÷2=84(平方厘米)
9×16=144(平方厘米)
84+144=228(平方厘米)
1
用分割法计算下面图形的面积。(单位:厘米)
(20-15)×(25-15)÷2=25(平方厘米)
15×25=375(平方厘米)
25+375=400(平方厘米)
2
用添补法计算组合图形的面积。(单位:厘米)
(10+20)×22÷2
=30×22÷2
=660÷2
=330(平方厘米)
8×6÷2
=48÷2
=24(平方厘米)
330-24=306(平方厘米)
2
用添补法计算组合图形的面积。(单位:厘米)
13×20=260(平方厘米)
12×5÷2
=60÷2
=30(平方厘米)
260-30=230(平方厘米)
求组合图形面积的基本方法
1.观察分析组合图形可分割或添补成哪些已经学过的基本图形。
2.找出计算基本图形面积需要的条件。
3.利用合理的方法,先计算出基本图形的面积,再计算出组合图形的面积。
填一填。
1
(1)计算组合图形的面积时,我们先要把它(
)成我们以前学过的(
)。然后分别计算出它们的面积,最后再把结果进行加或减。
(2)求下面图形的面积是(
)
(已知条件如图中所示,单位:cm).
割补
基本图形
9平方厘米
(1)计算组合图形的面积也要用到基本图形的面积公式。(
)
(2)用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。(
)
(3)任何两个三角形都可以拼成一个四边形。
??(?
?)
×
√
√
判断。
2
(1)两个面积相等的正方形拼成一个长方形,拼接前后的面积(???
)。
A.?增大??B.?减少???C.?不变???D.?无法确定
(2)如图中的阴影部分面积是(?
)平方厘米
A.?144?????????????B.?72?????????C.?18????????D.?无法确定
?????????????????????????????????
???????????????????????????????
3
选择。
?C
B
一块菜地(如下图),求它的面积。(单位:m)
4
18×18÷2=162(平方米)
(18+12)×22÷2=330(平方米)
162+330=492(平方米)
答:它的面积是492平方米。
一块稻田,中间有一条水渠通过。
5
(1)实际种水稻的面积是多少平方米?
(48+44)×21÷2=966(平方米)
1.5×21=31.5(平方米)
966-31.5=934.5(平方米)
答:实际种水稻的面积是934.5平方米。
一块稻田,中间有一条水渠通过。
5
(2)如果每平方米稻田产水稻1.2千克,那么这块稻田共产水稻多少千克?
934.5×1.2=1121.4(千克)
答:这块稻田共产水稻1121.4千克。
