冀教五年级上册数学9.1鸡兔同笼问题 课件
文档属性
| 名称 | 冀教五年级上册数学9.1鸡兔同笼问题 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-28 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
探索乐园
第1课时
鸡兔同笼
课堂导入-新知探究-课堂练习-课堂小结-课堂作业
冀教版
数学
五年级
上册
1.理解掌握并会运用列表法和假设法解决问题。
2.通过自主探索,合作交流,让学生经历用不同的方法解决“鸡兔同笼”问题的过程,培养学生的逻辑推理能力。
3.使学生感受古代数学问题的趣味性,体会到“鸡兔同笼”问题在生活中的广泛应用,提高学习数学的兴趣。
今有雉兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
这四句话是什么意思呢?
鸡和兔各有多少只?
它们一共有22个头,70条腿。猜一猜吧!
我猜鸡有10只,兔有12只。
不对,那才有68条腿。
把你的做法和同学交流一下。
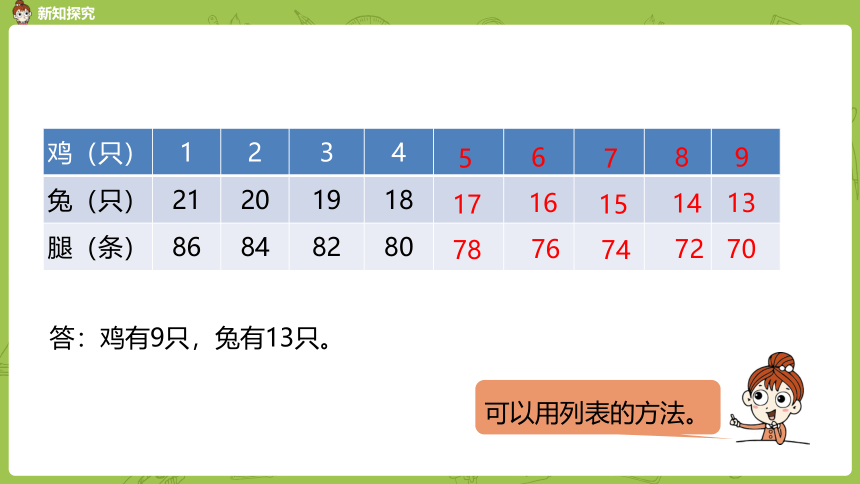
可以用列表的方法。
鸡(只)
1
2
3
4
兔(只)
21
20
19
18
腿(条)
86
84
82
80
5
17
78
6
7
8
9
16
15
14
13
76
74
72
70
答:鸡有9只,兔有13只。
还可以用方程解答:
4
x+2×(22-
x)=70
4
x+44-2
x=70
2x+44=70
2x=26
x=13
解:设兔有x只,那么鸡就有(22-
x)只。
兔的腿数+鸡的腿数=70条
鸡的只数:22-13=9
(只)
答:鸡有9只,兔有13只。
用假设法解答,比较简单。
方法1:假设这22只都是鸡。
(1)按22只鸡算,腿的数量是:22×2=44(条)。
(2)比鸡和兔的实际腿数少:70-44=26(条)。
(3)因为每只兔少算了2条腿,所以可以算出兔的只数:
26÷2=13(只)。
(4)鸡的只数:22-13=9(只)
。
用假设法解答,比较简单。
方法2:假设这22只都是兔子,可以这样计算:
(1)按22只兔算,腿的数量是:22×4=88(条)。
(2)比鸡和兔的实际腿数多:88-70=18(条)。
(3)因为每只鸡多算了2条腿,所以可以算出鸡的只数:
18÷2=9(只)。
(4)兔的只数:22-9=13(只)。
1
池塘里有龟和鸭共23只,它们的腿共有60条。龟和鸭各有多少只?
解:设龟有x只,那么鸭有(23-x)只。
4x+2×(23-x)=60
4x+46-2x=60
2x+46=60
2x=14
x
=7
答:龟有7只,鸭有16只。
鸭的数量:23-7=16(只)
1
池塘里有龟和鸭共23只,它们的腿共有60条。龟和鸭各有多少只?
答:龟有7只,鸭有16只。
假设这23只都是鸭。
(1)按23只鸭算,腿的数量是:
23×2=46(条)
(2)比鸭和龟的实际腿数少:
60-46=14(条)
(3)因为每只龟少算了2条腿,所以可以算出的龟只数:
14÷2=7(只)
(4)鸭的只数:23-7=16(只)
1
池塘里有龟和鸭共23只,它们的腿共有60条。龟和鸭各有多少只?
答:龟有7只,鸭有16只。
假设这23只都是龟。
(1)按23只龟算,腿的数量是:
23×4=92(条)
(2)比鸭和龟的实际腿数多:
92-60=32(条)
(3)因为每只鸭多算了2条腿,所以可以算出的鸭只数:
32÷2=16(只)
(4)龟的只数:23-16=7(只)
2
用100元钱购买下面两种洗涤液。(用列表法解答)
12元/瓶
8元/瓶
要正好花完100元,可以有几种买法,各买多少瓶?
2
用100元钱购买下面两种洗涤液。(用列表法解答)
12元/瓶
8元/瓶
设洗涤液1有x瓶,则洗涤液2数量是:(100-12
x
)÷8
洗涤液1(瓶)
0
1
2
3
4
5
6
7
8
洗涤液2(瓶)
12.5
11
9.5
8
6.5
5
3.5
2
0.5
1.“鸡兔同笼”问题可以用列表法、假设法、方程法等多种方法来解答。
2.假设法是假设——计算——推理——解答的过程;
方程法是根据“鸡兔同笼”问题的基本数量关系列出方程并求解。
填空题。
1
(1)用列表法解决问题。
鸡兔同笼,共有12个头,34条腿,鸡和兔各有多少只?
鸡(只)
1
2
3
4
5
6
7
8
9
兔(只)
11
10
9
8
7
6
5
4
3
腿(条)
46
44
42
40
38
36
34
32
30
从上表中得知鸡有( )只,兔有( )只。
7
5
填空题。
1
(2)用方程法解决问题。
鸡兔同笼,共有12个头,34条腿,鸡和兔各有多少只?
如果设兔有x只,那么鸡就有(
)只。兔的腿数是(
)条,鸡的腿数是(
)条。兔的腿数+鸡的腿数=(
)条,列方程为(
),解得х=(
),所以兔有(
)只,鸡有(
)只。
12-x
4x
2×(12-x)
34
4x+2×(12-x)
=34
5
5
7
填空题。
1
鸡兔同笼,共有12个头,34条腿,鸡和兔各有多少只?
(3)用假设法解决问题。
假设全是兔,那么腿的数量是(
)条,比实际腿数34条多了(
)条,因为每只鸡多算了(
)条腿,所以可以算出鸡有(
)只,兔有(
)只。
48
14
2
7
5
2
(1)大船限乘6人,小船限乘4人,38人共租了8条船,都坐满了。共租小船(
)艘。
A.
4
B.
5
C.
6
D.
9
(2)每只蛐蛐有6条腿,每只蜘蛛有8条腿,蛐蛐和蜘蛛共有10只,一共有68条腿。蛐蛐和蜘蛛各有多少只?(
)
A.
4,6
B.
6,4
C.
5,5
D.
3,7
选择题。
B
B
小明存钱罐里有1角和1元的硬币共18枚,共6.3元,请问1角和1元的硬币各多少枚?
1角=0.1元
(6.3﹣0.1×18)÷(1﹣0.1)
=4.5÷0.9
=5(枚)
18﹣5=13(枚)
答:1角的硬币有13枚,1元的硬币有5枚。
3
某次数学竞赛共20道题,评分标准是:每做对一题得5分,每做错或不做一题扣1分。小华参加了这次竞赛,得了64分。小华做对几道题?
假设全做对:
20×5=100(分)
100-64=36(分)
36÷(5+1)
=36÷6
=6(道)···错题
20-6=14(道)···对题
答:小华做对14道题。
4
自行车越野赛全程
220千米,全程被分为
20个路段,其中一部分路段长14千米,其余的长9千米。长9千米的路段有多少段?
假设全是9千米的路段:
9×20=180(千米)
220-180=40(千米)
40÷(14-9)
=40÷5
=8(段)···14千米路段
20-8=12(段)···9千米路段
答:长9千米的路段有12个。
5
探索乐园
第1课时
鸡兔同笼
课堂导入-新知探究-课堂练习-课堂小结-课堂作业
冀教版
数学
五年级
上册
1.理解掌握并会运用列表法和假设法解决问题。
2.通过自主探索,合作交流,让学生经历用不同的方法解决“鸡兔同笼”问题的过程,培养学生的逻辑推理能力。
3.使学生感受古代数学问题的趣味性,体会到“鸡兔同笼”问题在生活中的广泛应用,提高学习数学的兴趣。
今有雉兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
这四句话是什么意思呢?
鸡和兔各有多少只?
它们一共有22个头,70条腿。猜一猜吧!
我猜鸡有10只,兔有12只。
不对,那才有68条腿。
把你的做法和同学交流一下。
可以用列表的方法。
鸡(只)
1
2
3
4
兔(只)
21
20
19
18
腿(条)
86
84
82
80
5
17
78
6
7
8
9
16
15
14
13
76
74
72
70
答:鸡有9只,兔有13只。
还可以用方程解答:
4
x+2×(22-
x)=70
4
x+44-2
x=70
2x+44=70
2x=26
x=13
解:设兔有x只,那么鸡就有(22-
x)只。
兔的腿数+鸡的腿数=70条
鸡的只数:22-13=9
(只)
答:鸡有9只,兔有13只。
用假设法解答,比较简单。
方法1:假设这22只都是鸡。
(1)按22只鸡算,腿的数量是:22×2=44(条)。
(2)比鸡和兔的实际腿数少:70-44=26(条)。
(3)因为每只兔少算了2条腿,所以可以算出兔的只数:
26÷2=13(只)。
(4)鸡的只数:22-13=9(只)
。
用假设法解答,比较简单。
方法2:假设这22只都是兔子,可以这样计算:
(1)按22只兔算,腿的数量是:22×4=88(条)。
(2)比鸡和兔的实际腿数多:88-70=18(条)。
(3)因为每只鸡多算了2条腿,所以可以算出鸡的只数:
18÷2=9(只)。
(4)兔的只数:22-9=13(只)。
1
池塘里有龟和鸭共23只,它们的腿共有60条。龟和鸭各有多少只?
解:设龟有x只,那么鸭有(23-x)只。
4x+2×(23-x)=60
4x+46-2x=60
2x+46=60
2x=14
x
=7
答:龟有7只,鸭有16只。
鸭的数量:23-7=16(只)
1
池塘里有龟和鸭共23只,它们的腿共有60条。龟和鸭各有多少只?
答:龟有7只,鸭有16只。
假设这23只都是鸭。
(1)按23只鸭算,腿的数量是:
23×2=46(条)
(2)比鸭和龟的实际腿数少:
60-46=14(条)
(3)因为每只龟少算了2条腿,所以可以算出的龟只数:
14÷2=7(只)
(4)鸭的只数:23-7=16(只)
1
池塘里有龟和鸭共23只,它们的腿共有60条。龟和鸭各有多少只?
答:龟有7只,鸭有16只。
假设这23只都是龟。
(1)按23只龟算,腿的数量是:
23×4=92(条)
(2)比鸭和龟的实际腿数多:
92-60=32(条)
(3)因为每只鸭多算了2条腿,所以可以算出的鸭只数:
32÷2=16(只)
(4)龟的只数:23-16=7(只)
2
用100元钱购买下面两种洗涤液。(用列表法解答)
12元/瓶
8元/瓶
要正好花完100元,可以有几种买法,各买多少瓶?
2
用100元钱购买下面两种洗涤液。(用列表法解答)
12元/瓶
8元/瓶
设洗涤液1有x瓶,则洗涤液2数量是:(100-12
x
)÷8
洗涤液1(瓶)
0
1
2
3
4
5
6
7
8
洗涤液2(瓶)
12.5
11
9.5
8
6.5
5
3.5
2
0.5
1.“鸡兔同笼”问题可以用列表法、假设法、方程法等多种方法来解答。
2.假设法是假设——计算——推理——解答的过程;
方程法是根据“鸡兔同笼”问题的基本数量关系列出方程并求解。
填空题。
1
(1)用列表法解决问题。
鸡兔同笼,共有12个头,34条腿,鸡和兔各有多少只?
鸡(只)
1
2
3
4
5
6
7
8
9
兔(只)
11
10
9
8
7
6
5
4
3
腿(条)
46
44
42
40
38
36
34
32
30
从上表中得知鸡有( )只,兔有( )只。
7
5
填空题。
1
(2)用方程法解决问题。
鸡兔同笼,共有12个头,34条腿,鸡和兔各有多少只?
如果设兔有x只,那么鸡就有(
)只。兔的腿数是(
)条,鸡的腿数是(
)条。兔的腿数+鸡的腿数=(
)条,列方程为(
),解得х=(
),所以兔有(
)只,鸡有(
)只。
12-x
4x
2×(12-x)
34
4x+2×(12-x)
=34
5
5
7
填空题。
1
鸡兔同笼,共有12个头,34条腿,鸡和兔各有多少只?
(3)用假设法解决问题。
假设全是兔,那么腿的数量是(
)条,比实际腿数34条多了(
)条,因为每只鸡多算了(
)条腿,所以可以算出鸡有(
)只,兔有(
)只。
48
14
2
7
5
2
(1)大船限乘6人,小船限乘4人,38人共租了8条船,都坐满了。共租小船(
)艘。
A.
4
B.
5
C.
6
D.
9
(2)每只蛐蛐有6条腿,每只蜘蛛有8条腿,蛐蛐和蜘蛛共有10只,一共有68条腿。蛐蛐和蜘蛛各有多少只?(
)
A.
4,6
B.
6,4
C.
5,5
D.
3,7
选择题。
B
B
小明存钱罐里有1角和1元的硬币共18枚,共6.3元,请问1角和1元的硬币各多少枚?
1角=0.1元
(6.3﹣0.1×18)÷(1﹣0.1)
=4.5÷0.9
=5(枚)
18﹣5=13(枚)
答:1角的硬币有13枚,1元的硬币有5枚。
3
某次数学竞赛共20道题,评分标准是:每做对一题得5分,每做错或不做一题扣1分。小华参加了这次竞赛,得了64分。小华做对几道题?
假设全做对:
20×5=100(分)
100-64=36(分)
36÷(5+1)
=36÷6
=6(道)···错题
20-6=14(道)···对题
答:小华做对14道题。
4
自行车越野赛全程
220千米,全程被分为
20个路段,其中一部分路段长14千米,其余的长9千米。长9千米的路段有多少段?
假设全是9千米的路段:
9×20=180(千米)
220-180=40(千米)
40÷(14-9)
=40÷5
=8(段)···14千米路段
20-8=12(段)···9千米路段
答:长9千米的路段有12个。
5
